План-факт анализ в сводной таблице с Power Pivot и Power Query

523 05.05.2020 Скачать пример

Постановка задачи

В исходных данных имеем две таблицы. Скромную в дизайне, большую по размеру, но удобную в работе таблицу с фактическими значениями продаж, выгруженную из какой-нибудь учетной системы:

Фактические продажи

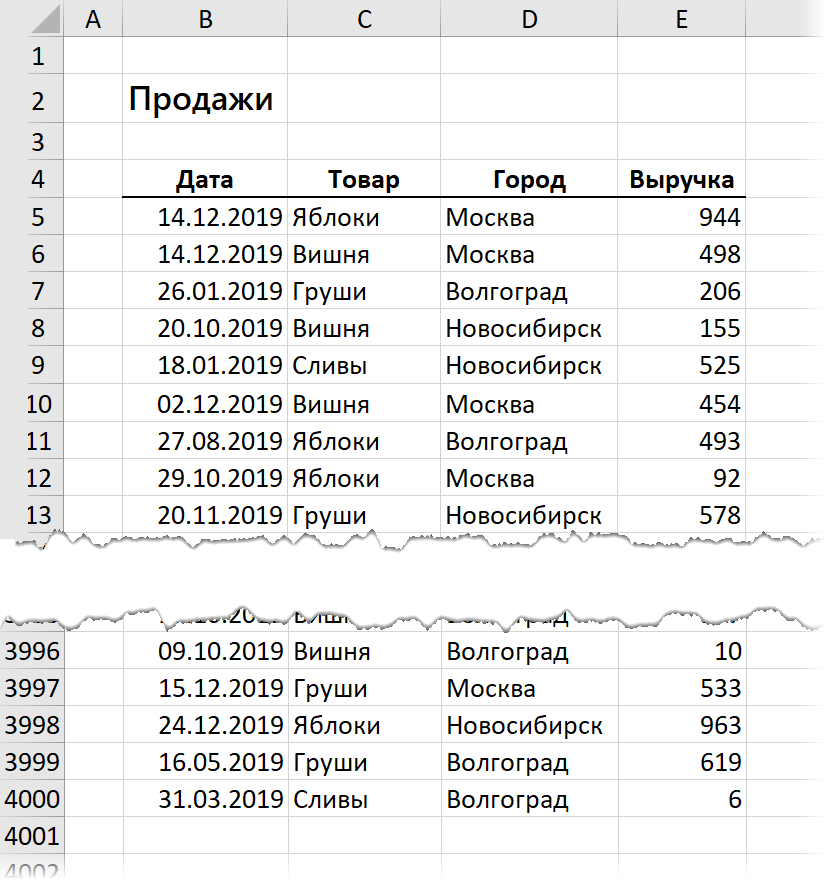
И "красивую" таблицу с плановыми помесячными показателями от руководства:

Таблица с планом

Задача: каким-то образом объединить обе таблицы в одну, чтобы наглядно отобразить выполнение плана по каждому товару, региону, месяцу, кварталу и т.д.

Необходимая оговорка

Можно, конечно, не напрягаться, и решать это дело привычным образом "в лоб". Т.е. с помощью 144 функций СУММЕСЛИМН (SUMIFS) вычислять суммарные продажи по каждому месяцу, товару и городу, а потом с помощью еще 144 формул вручную считать процент выполнения плана.

Потом мысленно взвыть, когда шеф скажет, что хотел видеть динамику по кварталам, а не по месяцам. И лучше в рублях, а не в процентах. И города лучше расположить по столбцам, а месяцы по строчкам. И не ной, у тебя вся ночь впереди, к утру чтоб было готово.

И в нашем примере всего 3 города и 4 товара. А если будет больше?

Давайте-ка лучше мы пойдем другим путем - чуть более сложным, но гораздо более гибким и удобным в перспективе.

Что мы будем делать

Думаю, никто не будет спорить, что самым удобным, гибким и мощным инструментом для анализа данных в Microsoft Excel являются сводные таблицы. Так что, в идеале, надо бы свести решение нашей задачи именно к ним.

Но как объединить в одной сводной две наших исходных таблицы? Плоскую таблицу продаж по дням и трехмерную таблицу плановых значений с детализацией по месяцам? Тут нам помогут 2 мастхэв надстройки для Excel:

  • Power Query - встроена в Excel, начиная с 2016-й версии, для более ранних Excel 2010-2013 её можно бесплатно скачать с сайта Microsoft.
  • Power Pivot - c 2013 года входит в состав большинства (но не всех, к сожалению) пакетов Microsoft Office. Для Excel 2010 (но не для более новых версий!) бесплатно качается, опять же, с сайта Microsoft.

Поехали, по шагам...

Шаг 1. Добавляем соединительные таблицы-справочники

Связать напрямую наши исходные таблицы факта и плана, к сожалению, никак не получится. Ни Power Pivot, ни, тем более, Excel не поддерживают пока связи "многие-ко-многим" (many-to-many), означающие, что в исходных таблицах могут встречаться дубликаты (а это как раз наш случай - названия товаров и городов встречаются в каждой таблице не по одному разу).

Поэтому нам потребуется создать "костыли" - промежуточные таблицы-справочники с уникальными значениями товаров, городов и дат, которые мы будем использовать для создания связей "один-ко-многим" (one-to-many), которые Power Pivot умеет делать на ура:

Соединительные таблицы

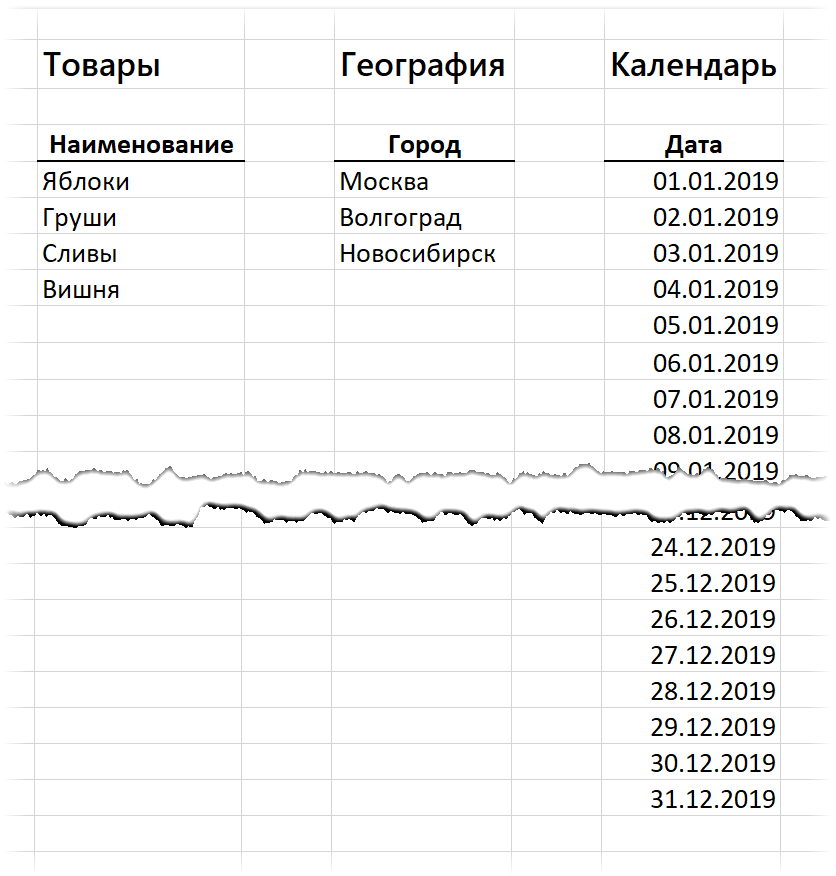
Для создания таблицы дат удобно использовать команду Главная - Заполнить - Прогрессия (Home - Fill - Progression):

Прогрессия для календаря

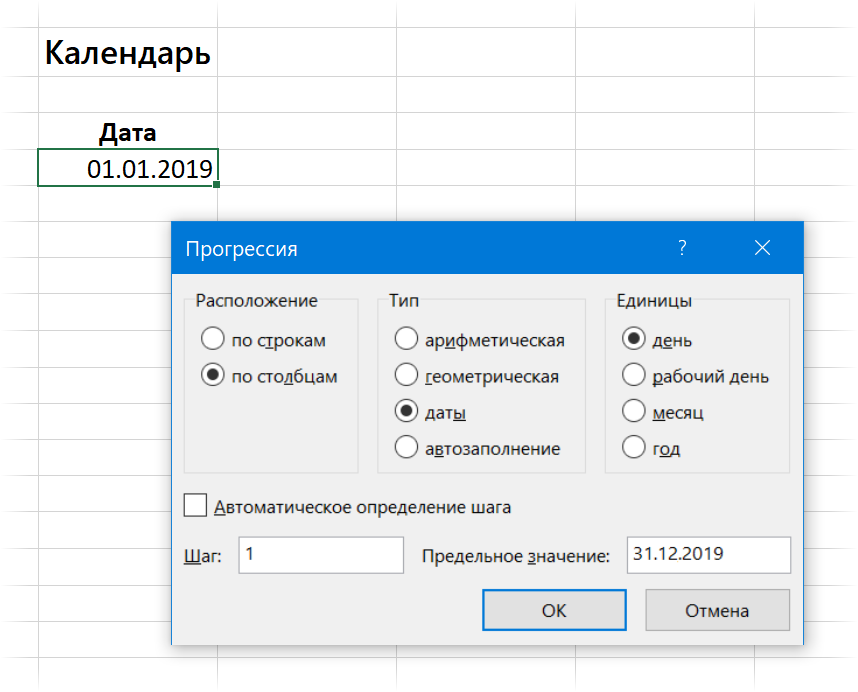
Шаг 2. Превращаем все таблицы в "умные" и даём им имена

Для загрузки таблиц в Power Pivot они должны быть "умными" (динамическими). Для этого с каждой таблицей проделываем следующее:

  1. Выделяем любую ячейку таблицы
  2. Жмем сочетание клавиш Ctrl+T или выбираем Главная - Форматировать как таблицу (Home - Format as Table).
  3. В открывшемся окне проверяем корректность выделения диапазона (особенно для таблицы плана!) и включена ли галочка Таблица с заголовками (My table has headers) и жмем ОК.
  4. На вкладке Конструктор (Design) в левом верхнем углу даем таблице осмысленное имя вместо стандартных безликих Таблица1,2,3...

Я назвал наши таблицы, соответственно:

  • таблПродажи
  • таблТовары
  • таблГеография
  • таблКалендарь
  • таблПлан

Шаг 3. Грузим первые 4 таблицы в Power Pivot

Первые четыре таблицы у нас в правильном виде, поэтому их можно смело загружать их в Модель данных - область памяти, с которой оперирует Power Pivot. Подключаем нашу надстройку через Файл - Параметры - Надстройки - Надстройки COM - Перейти (File - Options - Add-ins - COM Add-ins - Go) и убеждаемся, что на ленте появилась вкладка Power Pivot.

Теперь по очереди для каждой из первых четырёх таблиц, установив в неё активную ячейку, жмём на кнопку Добавить в модель данных (Add to Data Model):

Добавляем таблицы в Power Pivot

В старых версиях эта кнопка называлась Связанная таблица (Linked table).

В итоге все наши таблички должны загрузиться в открывшееся окно Power Pivot на отдельные вкладки:

Загруженные в Power Pivot таблицы

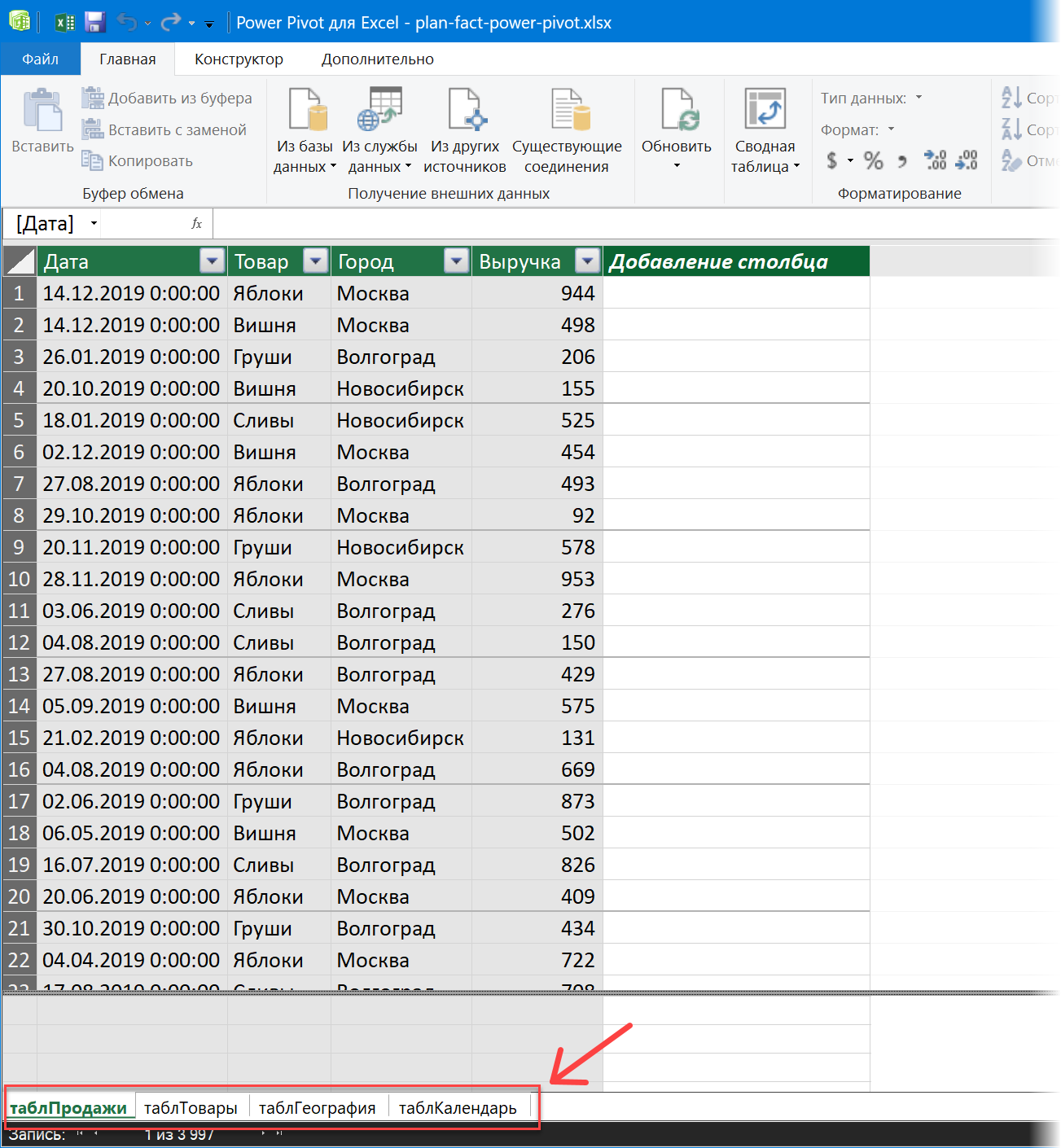
Шаг 4. Доводим до ума таблицу План

Прежде, чем загрузить в Модель данных Power Pivot таблицу с плановыми значениями, её нужно сначала подрихтовать: убрать в ней пустые строки и итоги, развернуть в плоскую, заполнить пустые ячейки в первом столбце городами и т.д. Проще и легче всего это проделать с помощью надстройки Power Query.

Сначала загрузим таблицу с планами в редактор запросов Power Query, используя кнопку Из таблицы/диапазона (From Table/Range) на вкладке Данные (Data) или на вкладке Power Query (если у вас старая версия Excel 2010-2013 и вы установили Power Query как отдельную надстройку):

Загруженная в Power Query таблица плана

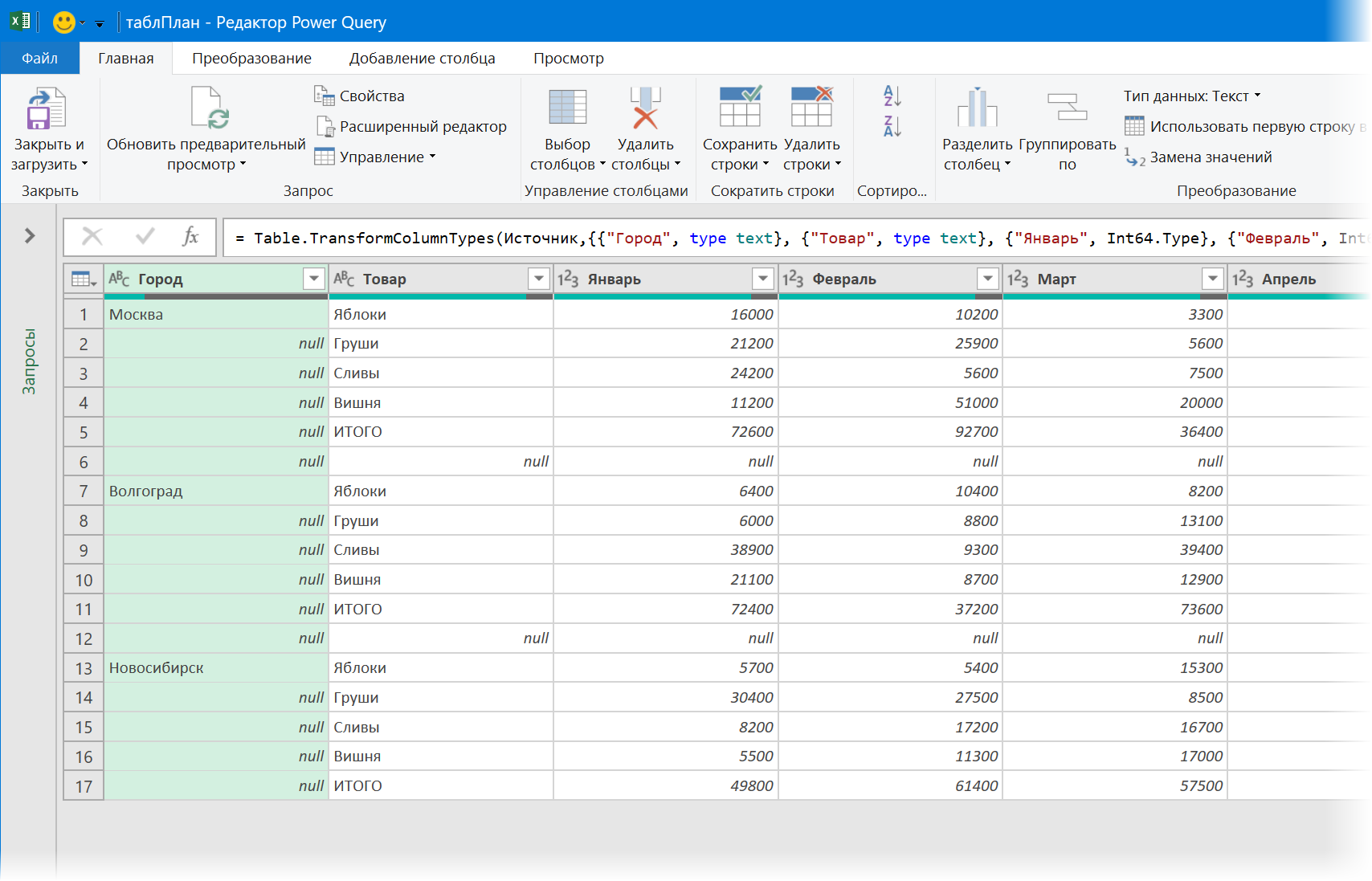
Затем в открывшемся окне Power Query делаем следующее:

1. Удаляем все пустые строки с null через Главная - Удалить строки - Удалить пустые строки (Home - Remove rows - Remove empty rows).

2. Удаляем строки с итогами, сняв соответствующую галочку в фильтре по столбцу Товар.

3. Удаляем ненужный последний столбец ИТОГО, щелкнув по его заголовку правой кнопкой мыши - Удалить (Remove).

4. Заполняем пустые ячейки в первом столбце названиями городов из вышестоящих ячеек, щелкнув по заголовку столбца Город правой и выбрав Заполнить - Вниз (Fill - Down).

5. Разворачиваем 12 столбцов-месяцев в два: название месяца и его значение. Для это выделяем первых два столбца Город и Товар (удерживая клавишу Ctrl), щёлкаем по их заголовку правой и выбираем команду Отменить свёртывание других столбцов (Unpivot Other Columns).

6. Чтобы преобразовать текстовые названия месяцев в нормальную даты - идём на хитрость:

  • Добавляем перед датами единички через пробел с помощью команды Преобразование - Формат - Добавить префикс (Transform - Format - Add prefix)
  • Аналогично добавляем после дат 2019 через Преобразование - Формат - Добавить суффикс (Transform - Format - Add suffix)
  • Теперь, когда текст в этом столбце стал уже гораздо больше похож на дату, конвертируем всё его содержимое в даты, используя выпадающий список типов в шапке столбца:

    Конвертируем месяцы в даты

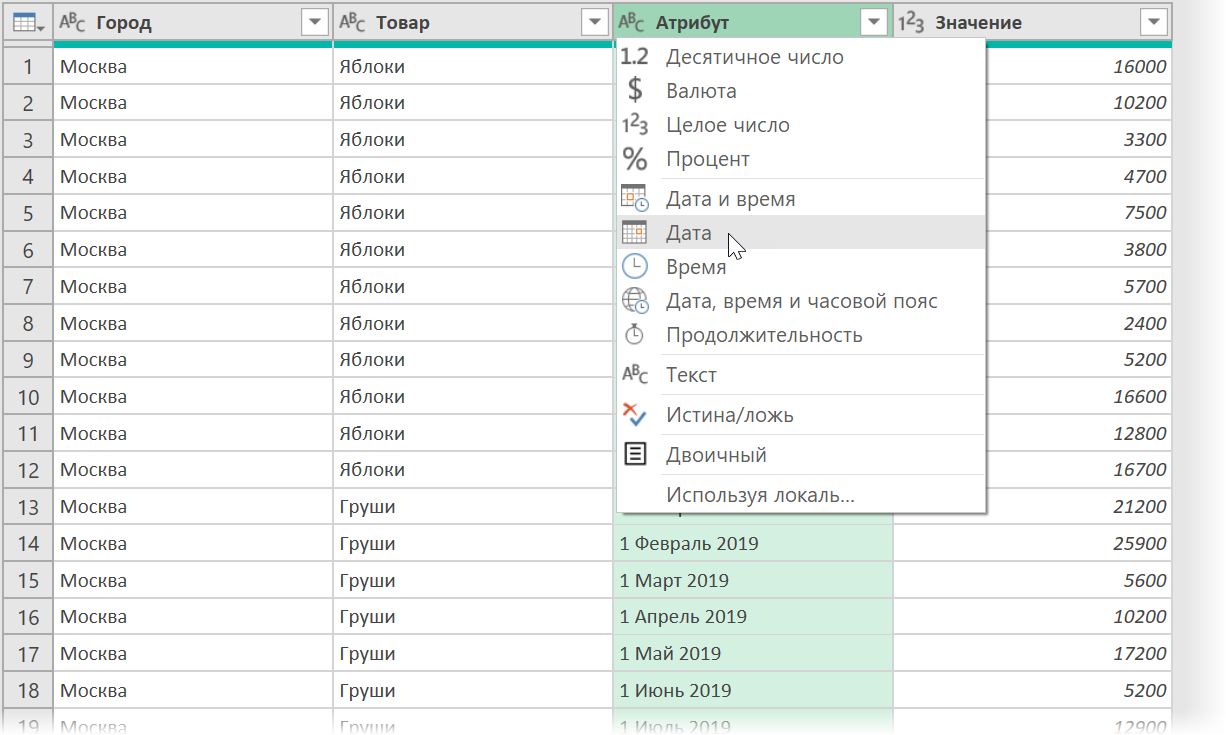
7. Столбец Атрибут переименовываем в Дата (двойным щелчком по заголовку столбца).

8. Чтобы не путать исходную таблицу плана с преобразованной, изменим имя запроса на таблПлан2 в правой панели Power Query (впоследствии это будет именем таблицы в Power Pivot).

9. Выгружаем готовую таблицу в Модель данных Power Pivot, используя команды Главная - Закрыть и загрузить - Закрыть и загрузить в... (Home - Close&Load - Close&Load to...) и выбираем затем в следующем окне опцию Только создать подключение (Only create connection) плюс, самое главное (!), включаем флажок Добавить эти данные в модель данных (Add this data to Data Model):

Загружаем результаты в Power Pivot                  Импорт данных

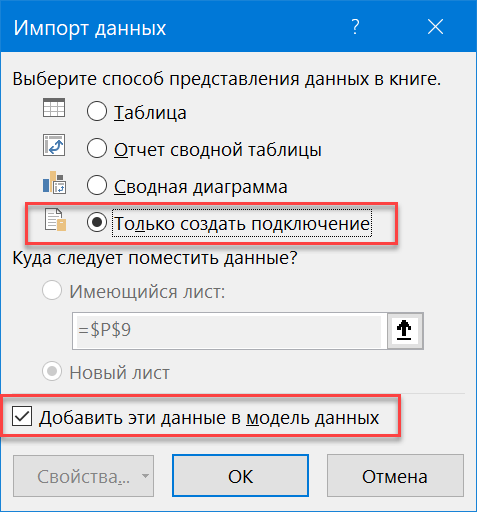
После этого наша последняя таблица таблПлан должна загрузиться в окошко Power Pivot.

Шаг 5. Связываем таблицы

Теперь пришло время выполнить одно из самых важных действий - связать все имеющиеся у нас таблицы в единую модель, чтобы впоследствии иметь возможность строить сводную по всей модели, будто это одна таблица.

Для связывания в окне Power Pivot лучше переключиться в режим диаграммы с помощью кнопки Главная - Представление диаграммы (Home - Diagram View) или значком Диаграмма (Diagram) в правом нижнем углу окна. Прямоугольные окошки таблиц можно перетащить за строку заголовка и разложить любым удобным вам образом.

Связь делается очень просто: хватаем мышью столбец в одной из соединительных таблиц (таблТовары, таблГеография, таблКалендарь), тянем и бросаем на соответствующий столбец в таблицах таблПродажи и таблПлан2:

Создание связи

Главный принцип: тянем от таблиц-справочников (Товары, География, Календарь) к таблицам факта и плана. Делаем 6 связей - каждый справочник должен быть связан двумя связями с таблицами плана и продаж. В итоге должна получиться вот такая картина:

Модель данных

Обратите особое внимание на положение единичек и звёздочек на концах связей - это как раз и есть те самые связи "один-ко-многим", где звёздочка обозначает множество вхождений одного и того же элемента, а единичка - уникальность.

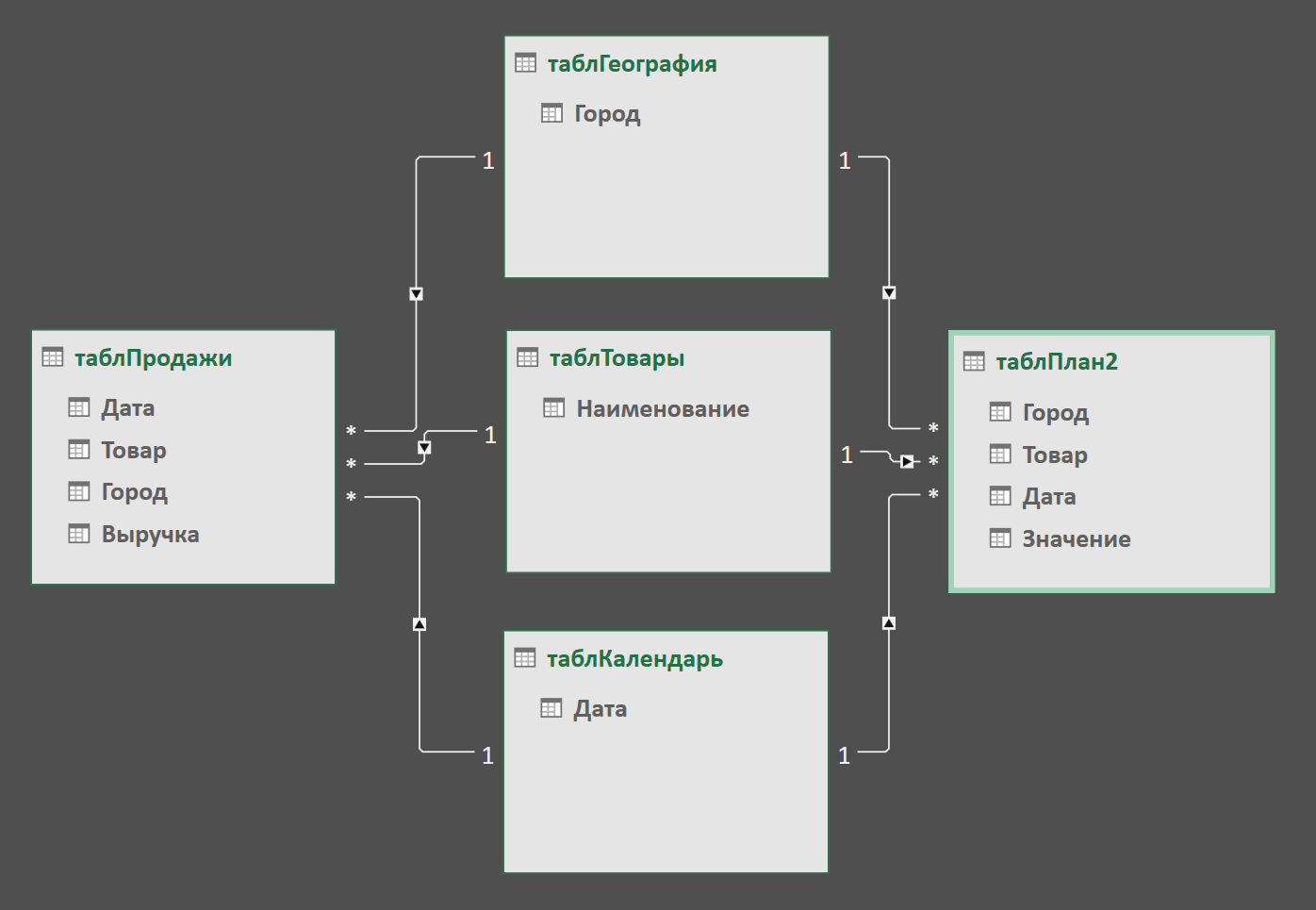
Если всё получилось, то сохраняем файл и выдыхаем - дело почти сделано.

Шаг 6. Строим сводную

Теперь на основе созданной модели данных можно построить сводную - для этого в окне Power Pivot выбираем команду Главная - Сводная таблица - Сводная таблица (Home - Pivot table - Pivot table). Мы автоматически вернёмся в Excel, где увидим привычную панель для построения сводной таблицы в правой части экрана, но в ней будут видны уже все таблицы, а не только текущая (как обычно):

Строим сводную

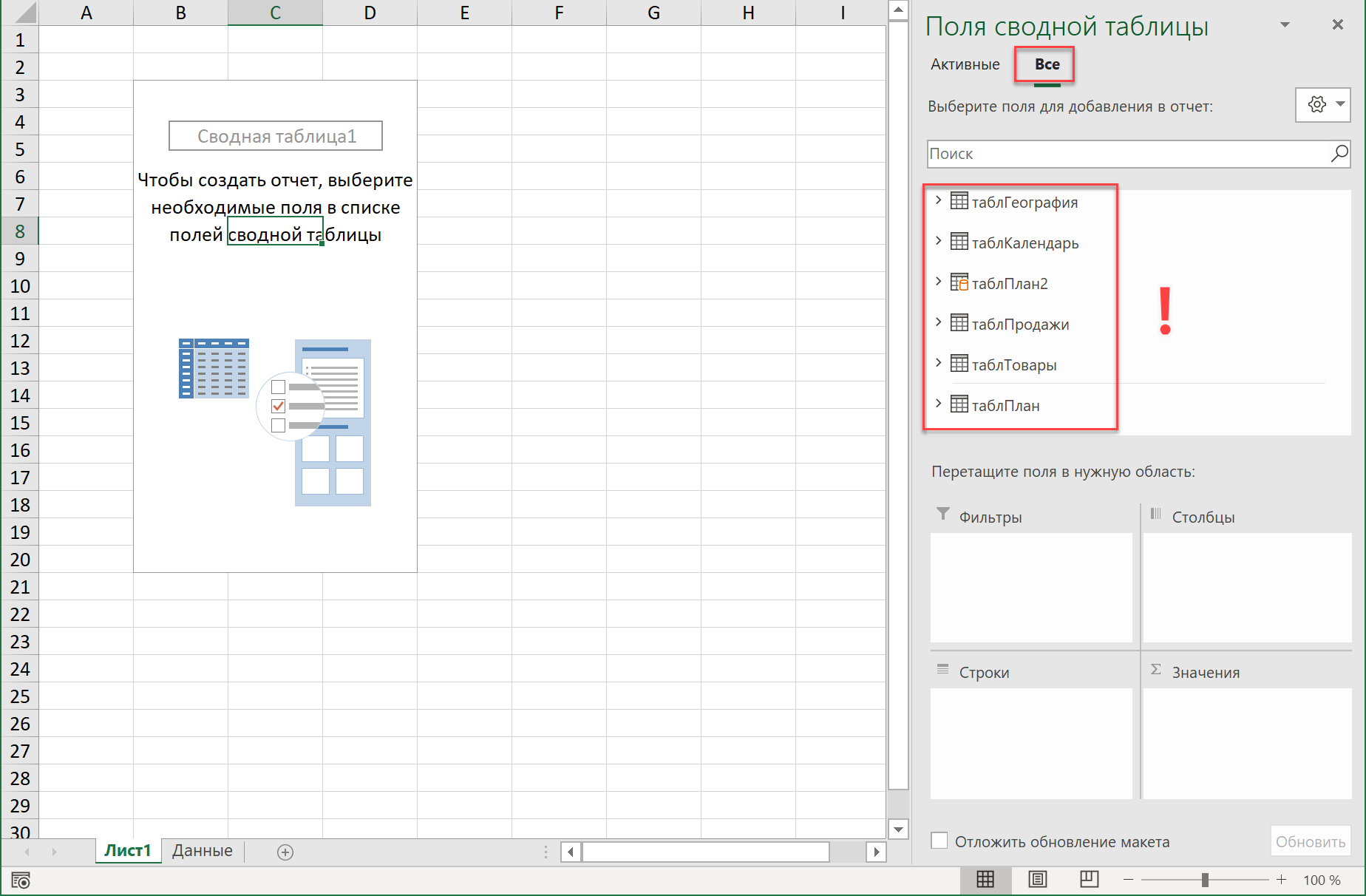
Теперь можно знакомым уже образом перетащить мышью нужные нам поля из таблиц в области сводной таблицы.

Главные принципы здесь такие:

  • В области строк, столбцов и фильтра можно бросать только поля из таблиц-справочников (таблГеография, таблКалендарь, таблТовары).
  • В область значений, где идут вычисления, можно закидывать только поля из таблиц факта и плана (таблПродажи, таблПлан2)

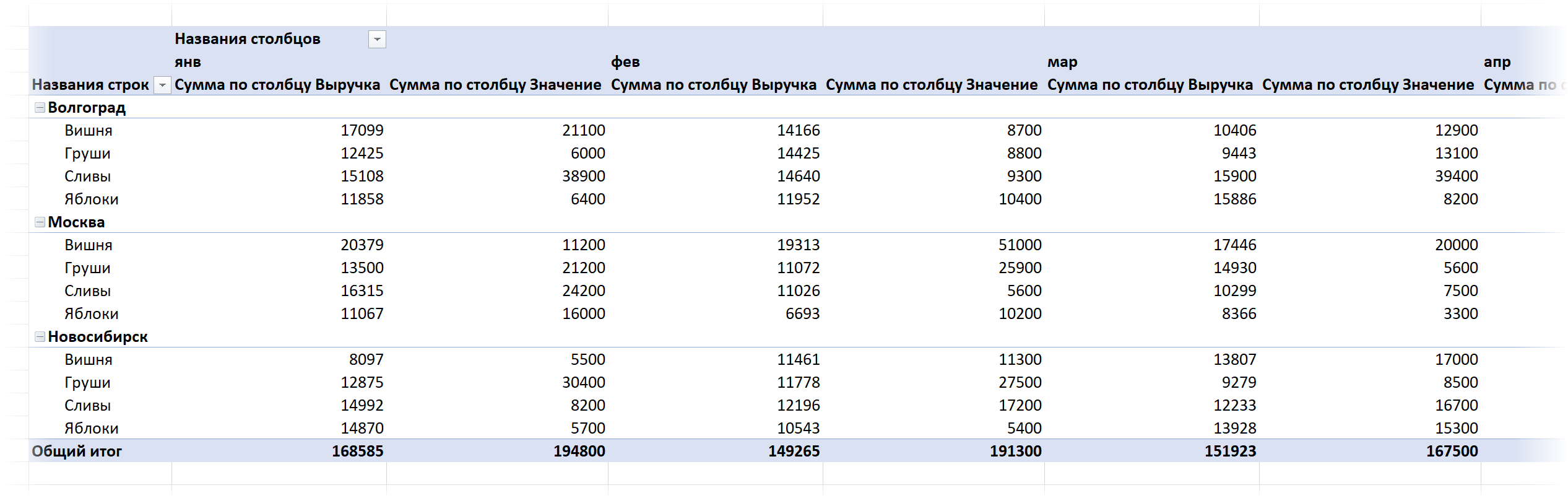
Например, можно накидать так:

Переносим поля в сводную

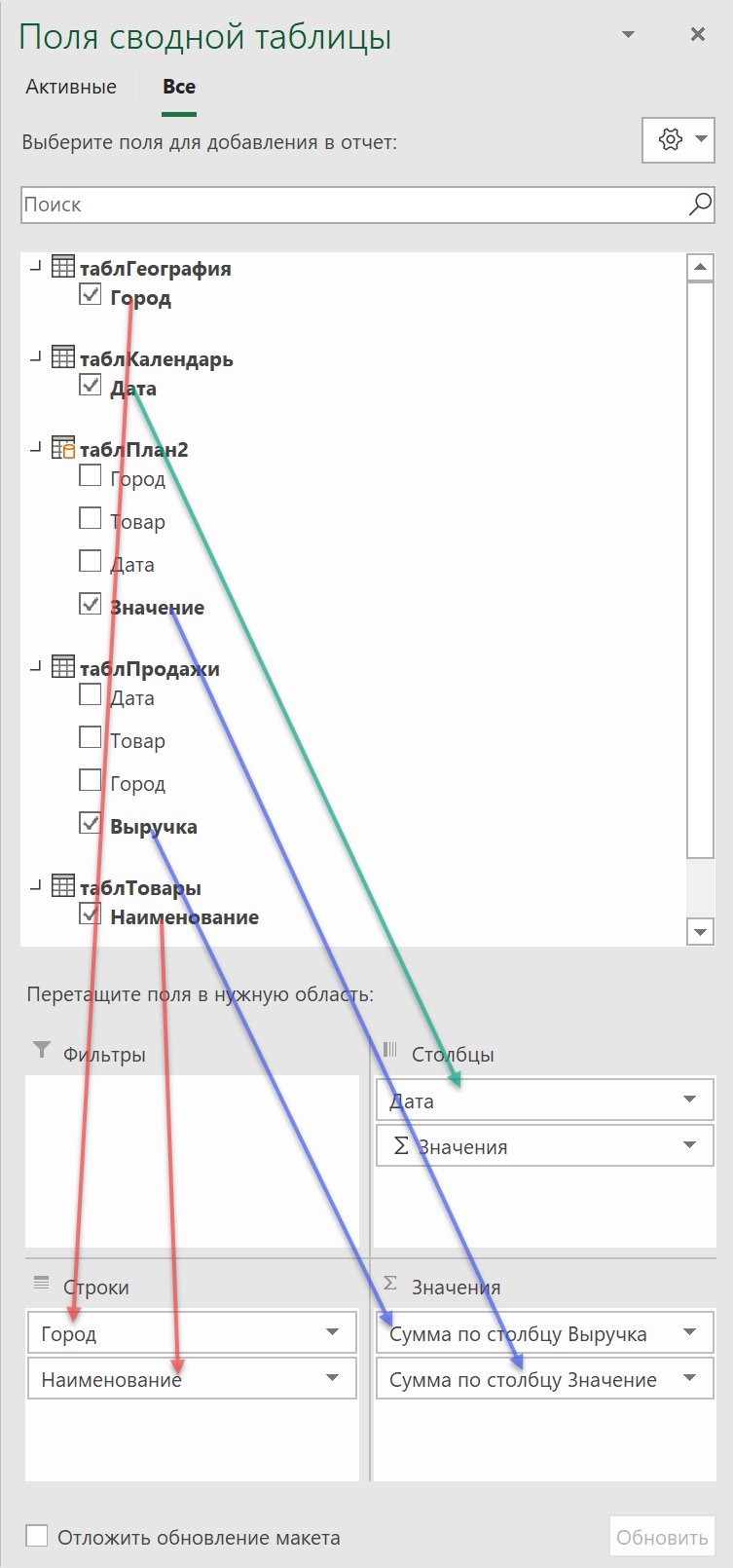
Чтобы по столбцам даты шли не с шагом один день, а покрупнее - щёлкаем по любой дате в сводной правой кнопкой мыши и выбираем команду Группировать по (Group by), а затем любой нужный уровень группировки:

Группировка дат в сводной

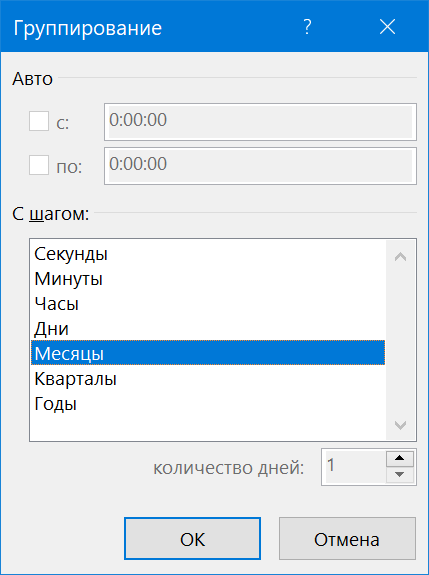
В итоге должно получиться что-то уже очень похожее на то, что нам требуется:

Почти готовая сводная

Шаг 7. Добавляем меры для вычислений

Меры - это, упрощенно говоря, формулы внутри сводных. На самом деле, когда мы переносим мышью любое поле (например, Выручка) в область значений сводной таблицы, то "под капотом" создается неявная мера - что-то вроде:

Сумма по полю Выручка := SUM(таблПродажи[Выручка])

Но контролировать процесс создания неявных мер мы не можем - Excel сам решает как её назвать, какую именно функцию (SUM или COUNT) использовать и т.д. Поэтому лучше создавать явные меры для сводной самостоятельно - в этом случае мы сможем контролировать все их параметры.

Для этого на вкладке Power Pivot выберем команду Меры - Создать меру (Measure - New measure) и в открывшемся окне задаём:

Создаем меру

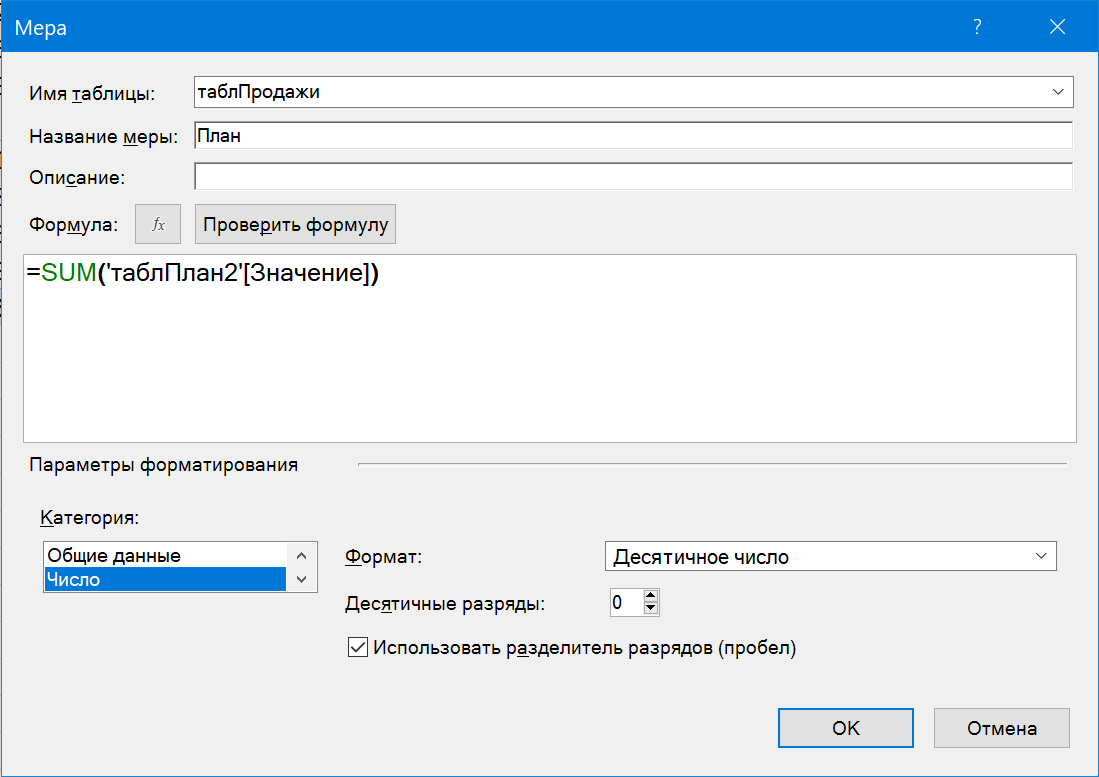
Здесь:

  • Имя таблицы - место для хранения меры (можно выбрать любую таблицу - это не играет роли).
  • Название меры - придумываем и вводим любое удобное название (можно на русском).
  • Описание - по желанию.
  • Формула - вводим формулу, по которой будет вычисляться мера. Можно использовать функции из встроенного в Power Pivot языка DAX (кнопка fx).
  • Проверить формулу - чекает вашу формулу на предмет ошибок и выдаёт рекомендации по их исправлению.
  • В нижней части окна можно сразу же задать числовой формат для меры, чтобы потом по 100 раз не настраивать его в сводной (как это бывает с обычными неявными мерами).

Повторяем процесс еще два раза:

  • Создаем меру с именем Факт с формулой =SUM('таблПродажи'[Выручка]) и числовым форматом без копеек и с разделителем.
  • Создаём меру Отклонение, которая использует две предыдущих созданных меры по формуле =[Факт]/[План]-1 и процентным форматом

Добавленные меры появятся в правой панели сводной таблицы с характерным значком:

Меры в панели сводной

Теперь их можно смело закидывать мышкой в нашу сводную и выполнять план-факт анализ в любых разрезах за считанные секунды:

Итоговая сводная

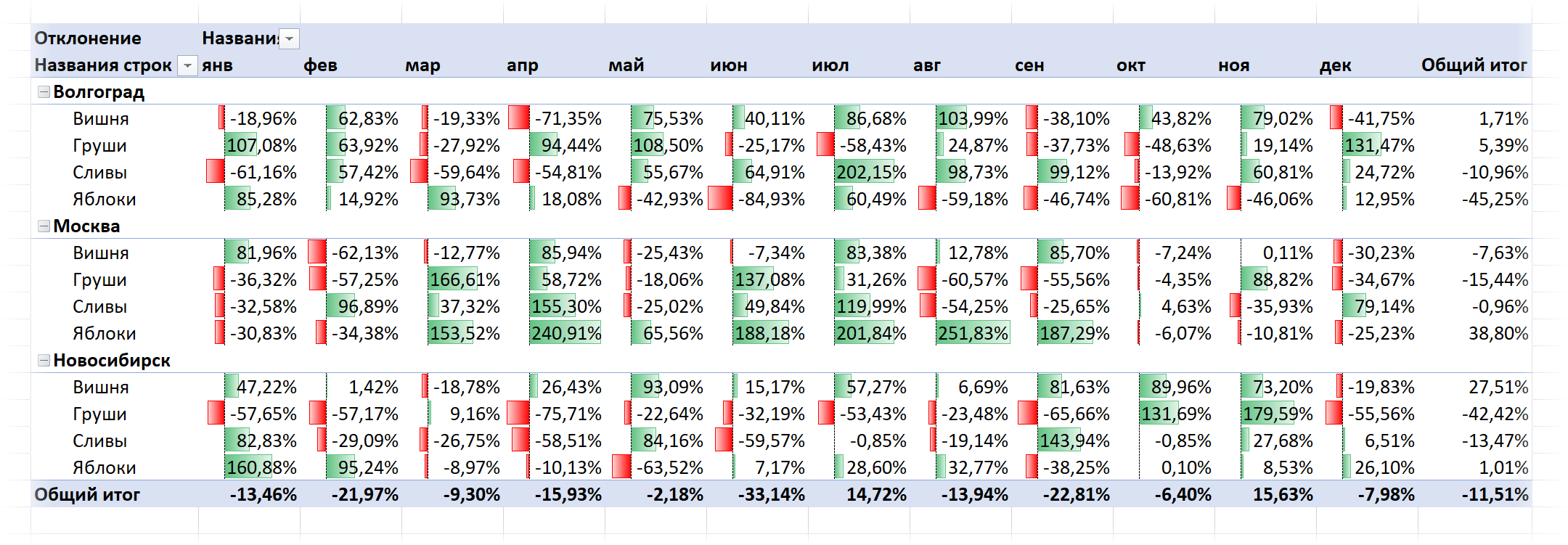
Обновляется вся созданная красота (модель данных Power Pivot, запрос Power Query и сама сводная) одним движением - на вкладке Данные (Data) с помощью кнопки Обновить все (Refresh All) или сочетания клавиш Ctrl+Alt+F5.

Возможные проблемы и их решения

В процессе реализации вы можете нарваться на несколько типичных "граблей":

  • Появляются странные ошибки в Power Pivot или сама вкладка Power Pivot неожиданно пропадает из Excel - отключите надстройку, перезапустите Excel и подключите её заново (см. Шаг 3). Обычно помогает.
  • Не получается создать связь - проверьте, нет ли повторов в справочниках. В столбцах, используемых для связывания не должно быть (в таблицах-справочниках) дубликатов - это жёсткое требование Power Pivot.
  • Какие-то странные результаты получаются в сводной - проверьте 1) правильно ли вы настроили связи 2) те ли поля вы используете для сводной (в области строк, столбцов и фильтра могут лежать только поля из справочников).

Если будут ещё какие-то сложности - пишите в комменты.

В любом случае, попробовать стоит - создав единожды такую обновляемую аналитическую систему, можно ещё долго радоваться ей в будущем :)

Ссылки по теме

 


Виктор Косенков
11.05.2020 21:42:10
Возможно - опечатка?
В Шаге 5 "Делаем 6 связей - каждый справочник должен быть связан тремя связями с таблицами плана и продаж."
Каждый справочник связывается с таблицами плана и продаж двумя связями.
Ссылка
Николай Павлов
11.05.2020 22:44:07
Спасибо, Виктор! Подправил.
Родитель Ссылка
Олег Хайруллин
11.05.2020 22:44:55
Николай, добрый вечер. Дома офис 365, power pivot есть, а на работе офис 2016 профессионал коробочный (кастрированный), там в надстройках отсутствует power pivot. Если я на домашнем создам сводную с план факт анализом, используя power pivot, то смогу ли потом пользоваться этим файлом на рабочем компе с кастрированным офисом?
Ссылка
Николай Павлов
12.05.2020 09:57:23
Нет, к сожалению.
Родитель Ссылка
Алексей Семилетов
12.05.2020 14:33:05
Николай, уверены? На сколько я в курсе отчет откроется и можно будет даже со сводной поиграться, но доступа к модели данных не будет, это да.
Родитель Ссылка
Николай Павлов
12.05.2020 23:55:03
Тогда уточните, что вы понимаете под термином "пользоваться" :)
Я имел ввиду полную функциональность, включая обновление, а оно работать не будет.
Если нужно только поиграться (подвигать туда-сюда поля в сводной, пофильтровать и т.д.), то это работать будет, т.к. сводная кэширует в себе эти данные (если вы не сняли в её параметрах галочку Сохранять данные вместе с таблицей).
Родитель Ссылка
Олег Хайруллин
13.05.2020 11:07:13
Спасибо за ответы, попробовал менять не получается на урезанном офисе, работа только со сводной таблицей так как она в кэше все держит, Николай правильно все истолковал: пользоваться - это полная функциональность + обновление
Родитель Ссылка
Алексей Семилетов
12.05.2020 15:21:01
Николай, класс! Будет куда новичков с форума отправлять. Надеюсь вы будете углублять тему РР, очень он востребован, а на русском внятной инфы маловато.

Не с точки зрения критики, а дополнительной информации для (уверен вы это все знаете, просто не хотелось раздувать статью):
1. При создании связей без разницы от какой таблицы к какой её тащить, РР сам разберется где один, а где много. Причем если с обеих сторон будут уникальные значения по ключевым столбцам, то заранее вообще не очевидно какую из таблиц он сделает стороной один, частенько он им назначает таблицу с фактами.
2. Календарь можно создавать штатными средствами РР
3. В столбцах, используемых для связи не должно быть не только дубликатов на стороне один, а также пустых ячеек, иначе будет ошибка.
4. При удалении дубликатов силами Power Query перед загрузкой в модель необходимо пристальное внимание обратить на тот факт, что PQ чувствителен к регистру по умолчанию, а РР - нет. Так что могут быть казусы, когда думаешь что дубликаты удалил, а по факту - вот они! :)
5. Это уже мое личное мнение из полученного опыта, лучше всего файл с отчетом делать отдельным от источников, в самом файле имеет смысл держать только таблички с настройками только для этого отчета. Все остальное тащить исключительно извне.
Ссылка
Николай Павлов
12.05.2020 23:59:08
Спасибо за ценные уточнения, Алексей!

Очень правильные комментарии, поддерживаю по всем пунктам.

Единственное, по п.1 у меня, по опыту, PP часто лажает со связями, если тащить их в неправильном направлении. Поэтому и акцентировал, что тащить надо от справочников - для надежности.
Родитель Ссылка
Алексей Семилетов
13.05.2020 16:41:14
Просто, вот буквально вчера тащил от одного справочника к другому, с обеих сторон уникальные значения в столбцах, и все равно стороной один, РР назначил ту таблицу, к которой тащил связь. Такое у меня в 2016, и в О365. Так что все не так однозначно! :D
Родитель Ссылка
Николай Павлов
19.05.2020 10:51:43
Странно. Сейчас еще потестирую у себя.
Родитель Ссылка
Алексей Семилетов
20.05.2020 10:38:19
У меня есть стойкое подозрение что в таких случаях качестве справочника на стороне 1, он выбирает таблицу, в которой больше строк.
Родитель Ссылка
Игорь Сухов
11.08.2020 01:35:30
Николай, здравствуйте!
Подскажите, как создать сводную табл из Power Pivot в другой книге?
В настройках можно выбрать только два варианта: на текущем листе или на новом, а в новой книге или в другой книге - нет выбора.
Это вопрос по п.5 в комментариях Алексея.
Родитель Ссылка
Анастасия Бережная
18.05.2020 19:40:19
Здравствуйте!

Загрузите, пожалуйста, исходный файл для примеры - чтобы мы "руками" могли все сами проделать, руководствуясь видеоуроком. Тот пример, который загружен Вами, уже содержит все выполненные шаги. Хочется поучиться все это делать самой на исходных данных.

Спасибо огромное!
Ссылка
Николай Павлов
19.05.2020 10:51:18
Не вопрос - по ссылочке в заголовке теперь лежит архив с двумя файлами - исходным и сделанным.
Практика - это очень правильно :)
Родитель Ссылка
Анастасия Бережная
19.05.2020 17:51:23
Спасибо Вам огромное!
Ссылка
Сергей Мальковский
05.06.2020 20:03:53
Спасибо Вам большое!

Скажите, а если в данном примере в Плане города будут по английски например, а в факте по-русски?
Для связки нужно добавить в справочник второе поле?

Через 15 минут: проверил сам - да, второе поле работает.:)))

Так что теперь - просто спасибо большое!
Ссылка
Евгения
07.06.2020 17:19:17
подскажите, пожалуйста, как лучше строить модель данных, если планы (прогнозы) делаются каждый период до конца года и сравнивать надо факт с разными планами. Допустим с планом прошлого периода, с планом два периода назад, и с планом, созданным в начале года (основа бюджета)?
а также текущий план (прогноз) с планом (прогнозом) прошлых периодов.
Ссылка
Наталья Дунаева
11.06.2020 11:21:08
Николай, спасибо.
Вот прям как раз думала над такого рода проблемой!
:)
Ссылка
KIP
29.07.2020 13:40:16
Добрый день, Николай!
Такая ситуация, на основе данных я создал сводную таблицу, (напрямую, без создания моделей), то я не смогу создать меру без модели?
Ссылка
Николай Павлов
30.07.2020 10:35:20
Не сможете, к сожалению. Меры работают только в сводных на основе Модели Данных.
Родитель Ссылка
KIP
31.07.2020 05:24:26
Я понял, спасибо! Следовательно нельзя в сводных таблицах произвести математические операции между ячейками, допустим есть некая ячейка "Районный коэффициент", которая меняется взависимости от вводимого значения пользователем, а некая колонка сводной тоблицы "Зарплата" высчитывается перемножением ячейки "Районный коэффициент" на колонку "Оклад" сводной таблици?  
Родитель Ссылка
Виктор Кочетков
04.02.2021 21:02:32
Может стоит кое что из описанного сделать в исходных данных допостроениясводной, с помощью power query?
Родитель Ссылка
сергей в
25.08.2020 00:38:08
Если в строки св.табл. я вставляю поля из справочников, то получается, что во всех категории вставляются все подкатегории (справочники полностью вставляются). Даже если в категории 1 должно быть 10 подкатегорий, а в кат2 - 4 подкатегории. И срезы не работают в такой таблице. Или что я делаю не так?
Ссылка
Михаил Лебедев
25.11.2020 18:18:49
Решил поэкспериментировать. Не стал создавать промежуточные таблицы для связи, а создал запросы (3 шт.) с группировками по Городу, Дате (преобразовав даты в формат "начало месяца" ) и Товару. Все полученные с помощью этих запросов таблицы добавил в модель данных. Всё получилось в итоге то же самое, только на последнем шаге опция "Группировать / Разгруппировать" стала недоступной, вот, не знаю, почему. Связано это с моим экспериментом по замене таблиц на запросы или с чем-то еще...
Ссылка
Natalia Suvorova
10.12.2020 23:23:23
Здравствуйте, Николай!
Большое спасибо за полезную информацию!
Подскажите, пожалуйста, что делать, если после добавления в столбец Атрибут суффикса и префикса PowerQuery по прежнему не распознает данные как дату и выдает ошибку  
Ссылка
Алексей Суганов
24.12.2020 16:00:38
Здравствуйте, Николай!

У меня та же беда (Excel 2013) -  на последнем шаге опция "Группировать / Разгруппировать" стала недоступной, в вашем же файле. Вообще обратил внимание  - как только использую Модель данных - опция пропадает, если сразу накидываю  сводную - возможность группировки есть, для одной и той же таблицы. Как -то можно решить?
Ссылка
Алексей Суганов
12.01.2021 15:37:01
Николай, добрый день!

Поставили на рабочий ноутбук Exel 2016 проф+. Соответственно, новый вид редактора запросов PQ, но главная проблема в рамках этого видеоурока - во вкладке Формат нет команд Префикс и Суффикс. Подскажите - есть ли возможность добавить? И есть ли возможность настройки отображения (вида) обрабатываемой таблицы - так, раньше в углу столбца отображался, например, тип данных, было очень удобно...
Ссылка
Артур Шакиров
05.05.2022 09:47:04
как вышел из ситуации я: создал дубликат столбца с месяцами и в продублированном столбце заменил все наименования на "2019". Далее через вкладку добавление столбца объединил исходный столбец с месяцами со столбцом "2019". Далее получивший столбец преобразовал в дату
Родитель Ссылка
Олжас
05.02.2021 11:19:37
Добрый день!

Данный способ мне очень понравился и я его решил применить для План-Факт анализа семейного бюджета. И у меня возник небольшой вопрос. А можно ли вместо общего суммирования воспользоваться суммированием для каждого месяца отдельно? Поясню: в плане за январь стоит сумма 20 000 руб., в феврале 18 000 руб., в марте 25 000 руб. и т.д., а по факту сумма в каждом месяце может отличаться (отклонение)... В результате в сводной на основе модели данных PT я хочу видеть отклонение не от общей суммы запланированных расходов, а конкретно отклонение от месячного плана... Пример: Январь - план 20 000, факт 18 500, отклонение составило 7,50%.... и так для каждого месяца... Спасибо не равнодушным))
Ссылка
vitaleq
19.02.2021 18:16:10
Доброго дня Николай.
Выполнил шаг 6, но офис 365  выдает ошибку вместо даты. Перепроверил преведущие шаги все ок.
:D Все наладилось. Сменил локализацию формата даты в столбце.  
Ссылка
Дмитрий
29.03.2021 12:52:35
Добрый день!

Очень классный урок!
Хотелось узнать, если итоговая таблица имеет несколько категорий товаров, у каждого из которых свои подразделы.
Создавая меры на каждый период времени, чтобы видеть отличие всех сумм подразделов на каждый товар сразу - выставляю меры по сумме в целых числах, провожу вычисление (% от родительской суммы), но не получается создать меру разницы по вычислениям.
То есть вычитая из февраля - январь, получается только разница исходных мер (разница показателей двух месяцев в абсолютных числах).
Нужна разница вычисленных процентов, исходя из того, что за 100% берется показатель по каждому товару.

Подскажите, пожалуйста, как можно проводить вычисления с такими мерами?
Ссылка
Виктория Голубева
14.04.2021 16:41:00
Добрый день!
Нигде в инете не могу найти ответ на свою проблему.
Делаю выгрузку из гугл-таблицы с помощью Power Query. До февраля 2021г все было также, но все работало.
Теперь не работает ни старая выгрузка, ни новую не сделать, а также не работает выгрузка годичный давности. Ранее все работало...Выдает следующую ошибку, причем и при выгрузке  с помощью Power Query, даже из книги Excel, сохраненной из этой гугл-таблицы.
Подскажите в чем ошибка?

""Непредвиденная ошибка: Ссылка на объект не указывает на экземпляр объекта.
Подробные сведения:
  Microsoft.Mashup.Evaluator.Interface.ErrorException: Ссылка на объект не указывает на экземпляр объекта. ---> Microsoft.Mashup.Evaluator.Interface.ErrorException: Ссылка на объект не указывает на экземпляр объекта. ---> System.NullReferenceException: Ссылка на объект не указывает на экземпляр объекта.
 в Microsoft.Mashup.Engine1.Runtime.TextValue.New(String value)
 в Microsoft.Mashup.Engine1.Library.Excel.ExcelReaderOpenXml.CreateItemRecord(WorkbookItem workbookItem)
 в Microsoft.Mashup.Engine1.Library.Excel.ExcelReaderOpenXml.<>c__DisplayClass4.<ReadTablesUnguarded>b__3(Int32 i)
 в Microsoft.Mashup.Engine1.Runtime.ListValue.DemandArrayListValue.get_Item(Int32 index)
 в Microsoft.Mashup.Engine1.Runtime.BufferedListValue.BufferedValueReference.get_Value()""


Фото прикладываю.[IMG][IMG]
Ссылка
Маруся Маруся
24.06.2021 15:24:31
Спасибо большое за эту тему!!
Ссылка
Алексей
22.10.2021 11:15:25
Решил добавить 1 новый город (Сочи) и 1 новую категорию (Арбуз),
Теперь в сводной таблице все города пересекаются со всеми категориями - что является лишним (см. красные значения на скрине).
Как правильно строить модели данных, если в каждом городе свой ассортимент товара?
Ссылка
олег иванов
27.10.2021 12:53:29
Добрый день друзья, никто не подскажет как быть если в плане есть например категория апельсин, а в в факте ее нет, и вдобавок в факте есть арбуз, а соответственно в плане арбуза нет! Как будет выглядеть анализ план-факт в данном случае? Указывать 0 ? или как не совсем понимаю, спасибо
Ссылка
Кристина Алексеенко
17.12.2021 12:48:11
Добрый день, прошу помощи. В двух запросах PQ продажи по годам, есть ID магазина, создаю связь через справочник с ID магазина, при построении сводной PP связь не находит (цель - построить одну сводную для нескольких лет, сводить в PQ тяжело, т.к. детализация по неделям, даты недель скользящие от года к году).
Ссылка
Ольга Егорова
10.01.2022 22:49:31
Доброго дня! Почему при попытке ввести формулу меры =sum('табплан2'[Значение]) выходит ошибка Следующая формула DAX недопустима:

sum('табплан2'[Значение]), а далее "ссылка на объект не указывает на экземпляр объекта"?

Это происходит как в скачанном примере, так и в самостоятельно создаваемом файле.
Ссылка
Любовь
07.07.2022 14:14:47
Добрый день.
Николай, подскажите, плиз., что я сделала не так.
Репетирую на ваших же файлах. Результат: в сводной план по месяцам один и тот же. В каждом месяце сумма по товару - итог за 12 месяцев. Факт верный. Не знаю, как тут скрины приложить.
Ссылка
Ольга
23.02.2023 20:34:10
Добрый день.
Необходимо проверить везде формат ячейки - должно стоять "дата".
И в таблицах на обычных листах и в таблице в power query.
Родитель Ссылка
Любовь
15.03.2023 15:54:29
Спасибо, Ольга.
Родитель Ссылка
Юлия Калиниченко
22.09.2023 17:06:01
Добрый день! пожалуйста, подскажите, где может быть ошибка, когда при формировании сводной я добавляю сумму по движению ДС из Выписки и сумму по остаткам ДС, и они падают на разные столбцы и формируют дубли дат в столбцах, вместо того, чтобы подтягиваться по одному столбцу в ту дату, по которой есть совпадение движения. Заранее благодарю!
[IMG]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAA5kAAAMGCAYAAAB4ZkCwAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAANlJSURBVHhe7N0JfFTV3f/xLwoSCDuEBAFRQNZKkEWLCwi27C5PoUDVylJbCwoKuIJCVUCrAioIf5/aYKy2gvDUDURUMC5FZMeyCiqyhgQkhEAQkP89d5lMJjPJJExCls/79TqvzLnb3BmcON+c3z23XFpa2hkBAAAAABAB57k/AQAAAAA4a4RMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDElEtLSzvjPgYAlBG/fPI29xGAc+XLh19zHwFA6ULIBIAyyITMTU++4/YAFLVWD99IyARQalEuCwAAAACIGEImAAAAACBiCJkAAAAAgIghZAIAAAAAIoaQCQAAAACIGEImAAAAACBiCJkAAAAAgIghZAIAAAAAIqZcWlraGfcxAKCM+OWTt2nTk++4vezGjh3rPgrf1KlT3UcAwtHq4Rv15cOvuT0AKF0YyQQAAAAARAwhEwBQyJZq3MM3qtXDT2uJu0T/edoeyWn1ylJ3AQAAKC0ImQCAHEz5q9e6du2aa78glmz73P55c7Nu9k8AAFB6EDIBAEVsqT7Zan5eo+uushdYvNFOr43U33a4q7x1U1+TvZtlySvOduP+E7if28y29mipdZz/vKb+vnX+x806To51O/z3Mc0dhQ1c7huJ3aq/TfXbzix5d6S9Tf93l7rrApu1rXe8YCO6jPYCAEooQiYAIIf33nvP18Lp58fWd/+tt6yfra66Sd3tJSYoPmctu0bPPfmONj35jEbX2anpL2cPhMF10xR7n3t1s+nWGaB/m/7Y29TcXm8d590V6nGHteyOAWpl+m85YdUEzP+t/Yw9AZKzf9Y6n+b3uusfUHcTCF+ep03eshuusV7Mc1aIzLZHEPX1x7HmGOZ1mb73Oq1j2usBAChdCJkAgBz69u3ra+H0w/O57n34Rv3Pf3ZaAfMZzb/BiYH6z6qA0Nlcf+xkBTgr9H2wKa8Al7dWV92tPzaxHjTpqB4m5KWu0KdWeO0+5J2sc7CC4CX2ur3Wswa3ddMKbbJ++kp8r+pgB9tN21ZmD6YAAJRxhEwAQBFxR/BuuEab/nO/rwx068Fd9s88pc7T/7ilpvdGItVlK329X9NT3eUh7DzoxM+33vX2MaOvgZwgbdabMB22rc+5xzTNb4IkAABKIEImACCHwHLYvPr5ctVNTtno1n/b5bDNazd0lufFK4W12nPeAGSBNFSjJks1zpS++o7plbKG1qh2I/vnzTc45+BrvtJcwyuFfUf/vsrZPixeCa5d0msFVb/rTwEAKGkImQCAHALLYfPq509zdW5mAthOTf9saVbZ6X/edkfwtupvy83ss9foT75y1oLb9J+ZzrWdO1bqAzNaWedC5Yh/3rpcNG91pRUApbe2FcFEPLUv9AuuAACULIRMAECRa37D/zgT9WxdZQXLbprijeDZ5aKmdNWMCEZmYpxWzRvqg5et45qRSzPSaI88Ws9pJu7xSnBfXqFmzfMYeWxym+a7k/1klbaa2WMjMOboHdMbXR3CrV0AACVXubS0tDPuYwBAGfHLJ2+zyzODGTt2rPsofAW9X2ahMrcAeffz7JMMAcWE+aPClw+/5vYAoHQhZAJAGZRbyCw1CJkoxgiZAEozymUBAAAAABFDyAQAlE5XPWCP1jKKCQBA0SJkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAIioQ4cO5bsBAIDSo1xaWtoZ9zEAoIz45ZO3adOT77i9yBo7dqz7KHxTp051HwFlQ6uHb9SXD7/m9gCgdGEkEwAAAAAQMYRMACgtftqoV0f1U79Bj+jtne6yc6RWrVq+Fh0dnWs/b59o5uDBGjb4BSW5S/TJC1bfWvbCJ+4CGEkvmPdpsGb6vy3b5uoR816Nm6tv3EUAABQmQiYAlAIZHz6lfrf/S5Vvvkn13WXn0vjx433tiiuuyLVfEEkbVts/27W5zv4JAACKD67JxFlLSUlxHwEoCjExMe6jnH7a+Krue2Kbrv/rJN3UyF0YRGFfk/nEE0+4PWnp0qXq1q2b23P6ffv2dXvO9rlfk2lGMudojdprcOIodcnR99/GU189x0/RgGbmsbuufm89PGWgLrWWmBG/RCunths6VJrjv5/LbNs9WU/O2a+eQ+O1Yc4i7XVW+B036zgOv3Vm9HCyt4/hnmvg8vZDlTDKBOVtmjdushbvyXpN38wdpycX7dGFvYeqzfo51jp7Dz/+r9+R9boSdbeXv73nDPL6HUHO23deOY+Zta/f8/u9rgt7j9ekgc4bFP7zeK8/jPfQPDQj2XN8B3b4nXOOfcN6n7POuyhwTSaA0oyQibMyx/pytmzZMrv8DUDRmD17tvsop+ISMvv06eP2pGPHjqly5cpuz+mfTci8MEcoCAydgYElt5DphbGc22QFGfc4coOLu81e6xgfxgacg7d/kLCWI1i5x3deh8IIPzkDUqCcr8viPW8Bzts7B8M5pncO9iLf8/hv5wU651y8f4OAc8/x/gT8mwW815cG/hu7713g89v9C82+yfp1wPuY/fxze5+LBiETQGlGyESBmYC5du1aPfbYY6pZs6a7FMC5VFxCpn9ofO+997KFysB++CEzS7ZAkC2sBVu2N0eAzE/IzBny/EbbfPIKUYFhxyzxf87LtTbP8JMzIAXKPnIYwP+1+eRy3j2Tncfuls55e+fcXu20WmvizOu70D7Ghvjeilu0SGvs16wc72fOIBg6ZF6+NvC9CthfwUKmgvy7WPId5osGIRNAacY1mSiQzZs3a/ny5QRMAEGZ0UqvBesXjAkGiUoY2l57F032TfrzTfJ++2ee9izSk/YEQrkEsfwwgcw93rDBJri4y0PYm+xssGaOt48Vwuwl/lYr0T2mCT4FZcJXgnmvTBvfWxe6y21hnXey5r3ijCT2bO8u8hfXRj3i61unu0FJ29Zqg3WMuNhYZ93+ZH2zLVn2v4rfex709ayeE/Q8vPcqL957aR+7fXdfwDRh2zmu1ayAmVNk3mcAQHCETBTIzz//rLi4OAImgKC+/PJLXwvWPyvX9VRPM7vR6iWat026NDbOWZ4XM6rmBq/BwYJT2OIUa0pwvXJO+5jjnXPKxYWxzgbZAqBp2UYX3SBttYd7F8YUTmGe9+pFzqjikIFyo6PDDY8Xxl6oSy+Pt8Lran34ynrttc77susuVF1zrD3J2tss1nqXLH7vude8kUmbGckMch7ee5UX33s51PoHtQLrI3O32SOT3ii1b10Ohf0+A0DZRsgEAEScmejHa8H6Z6eZLjejaNqjxYs/sUJnG7WzensXLXZvcbJN85aY0av2+nUEyh/3LnrFDrNyR+xUPzb7yKDhrcuFE8qkNRsid9sVb8Qu2y1L8iOX876w95Ccpad7rQDpPlSzy9XG+mfYu8eMIrZRF+vfJSvvX6fLTLbbs15rzXuXT773aol325VP9IEZcbRCaw//kBoGbybi8GzXm+PNe/qI5u+Qdswbb7+/E960Otvn6VEz+vnIm/rW3RoAEBwhEwBKAfsWJv366XcT3taek5v16hjnfplfnaPJnw8dOuRrmZmZufYL4tKB3e1gaZdrWoHmbrsk1CuBzH7N3dm6sH2cNky2jmtfn2gd1x55tJ7TjJB55aCT1yuufR4jYs0GapI74uYr5bSaGX0rOmGed/uhuV6fGBdr1mWFyuy3ktmvZOsldRllRif3aLF573yv1+9ep7nx3itfuW3A9bIuX+mxKYl1z/nSgUPsUVFvXaL1b2b/twIAKDJM/IMC2bhxo+bOnavHH3/cXQKgJCnMiX8mT57sPnKcPHlSFSpUcHs5+0ZB75dZqIJNKARECBP/ACjNCJkoEEImULIVZsgsNQiZKESETAClGeWyAAAAAICIIWQCABDMdaPs2UcZxQQAIH8ImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCFkAgAAAAAihpAJAAAAAIgYQiYAAAAAIGIImQAAAACAiCmXlpZ2xn0MhG3jxo2aO3euHn/8cXcJgJLkl0/epv888prbA1DUrpp0m758mM8ggNKJkIkCIWQCJduI1ye7jwCcK7NuHe8+AoDShZCJAiFkAgAAAAiGazIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMeXS0tLOuI+BsG3cuFFz587V448/7i4BUNIcO3VC7+9b5fYAFKbK5SuqV70Obg8ASjdGMhG277//3g6Xpn333XfKyMjw9U0zfQAAAABlGyOZCNuECRPsMBmKGdVs3bq12wNQ3DGSCRQdRjIBlCWETITNhMx69eqpS5cu7pIs06ZN0+jRowmZQAniHzJjKlVX38ZX2Y8BRMbpn0/r1c1L7MeETABlCeWyyBdTJlu9enU7THpty5Yt+vHHH90tAAAAAJRlhEzky44dO5SUlOT2cvYBAAAAlG2ETOTbW2+9pf3799uPV6xYod27d9uPAQAAAICQiXw7ffq0EhISlJKSonfeecddCgAAAACETBTQqlWr9OSTT+qnn35ylwAAAAAAIRP5cMkll/gm+zGPzUim/wRA0dHR7pYAAAAAyipuYYICMffLnDt3rn1vTAAlE7cwAQoXtzABUFYxkgkAAAAAiBhGMlEgjGQCJV84I5mHDh3S5MmT3V54atWqpfHjx7s9oOxiJBNAWcVIJgAAAAAgYgiZAICilfJv/fHhG9XqyZe11l2U/OE4tbKWdV+wzvQ0b5a13mwT0LKv/4Oe32jvHvSYAADg3CBkAgByZcpfp06darcnnnhCvXv3DtkvWJlsspK++a/1M0Z9WrR1FtlidOdt72jTk1ltST//9VmS163UF9bPBs066HJnEQAAOEcImQCAcyvlP/pwl/WzWid1bu0syp9QIRUAAJwLhEwAQK5OnDih9957z25Lly7V8ePHc+2fOnXK3TMc6Vr+8UJ9ocr61S97FmgUMn3tAiVYIbXaJb9RvwKFVAAAEEmETABAripWrKi+ffvarVu3bqpUqVKu/fLly7t75uHIO7r14Vv1h/VH9avuz+qFrg3cFZ4UvfSa/zWZftdg2pz1V85brMOX3Kn5f+qjwCMAAICiR8gEAJwb1W7U60++o2XdGuujJSPcSX38+V2TOWaorjah8s2/6K197mpvvbXusu9eUncm/QEAoFggZAIAclW45bJSbKebNLiatPvrt/wCZICYq/TrhtbPE7u085CzyCfmVxoWX1c68pHmLNvtLgQAAOcKIRMAkKtCK5f1VGmlzpdYIfHEGs36T+BopivXyYGq6hfN2+kiHdNHXy5mNBMAgHOMkAkAOMeqqtP1fXS19Wj3tlV+IdHvmsxpc/SFKa99+I6gkwNVvbyfhpmRziPL9Wm26zYBAEBRK5eWlnbGfQyEbePGjZo7d64ef/xxdwmAkubYqRN6f98q+3FMperq2/gq+7G/Q4cOafLkyW4vPOa+mgW7XyZQupz++bRe3bzEfly5fEX1qtfBfgwApR0hEwVCyARKvnBCJoCCI2QCKKsolwUAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAIXm559/1qFDh/LVDh8+7O4NAABKonJpaWln3MdA2DZu3Ki5c+fq8ccfd5cAKGmOnTqh9/etsh/HVKquvo2vsh9HkgmNkydPdnvhqVWrlsaPH+/2gJLr9M+n9ermJfbjyuUrqle9DvZjACjtGMkEAAAAAEQMIRMAUKjOO+88e3TStJo1a6pKlSoh+zVq1HD3ysWBd/Xk4MEaNvpVbfAtmqxh1rKxr653lwAAgHOFkAkAKFQmOJryV9PGjBmjzp07h+zfdddd7l75cUBfbdhm/ayltvHxziIAAHDOEDIBAIXqzJkzOnbsmN0yMzNz9MuVK+duWUAHVuhrO2NeLl/G9EY7vfbnp/XBHnedJX3ly7rPf73VRjy9WH6b+EnXqpfH+G33lpb49bPaaP3DDKSmr1TCGL/l9ohr9mNkNWufL93t/UZms3j7ucc2gozkAgBQnBAyAQCF6uTJk/ryyy/ttmbNGp04cSJb/+xYIeydZfpGldSqx/VqYxaZEHb/fH1T63rdm5iohJl365rKGzX3iaygeXx/sg6ZfX43RQnP9NelzuIgTMibqFmfHXO2TZypYbW+0oYGY+3HI66tbW1TS13HWM+TOF2/b2wFxon/VIXBpp+o5+++VrUOfazEV79VhzumBd+ntf1E4TEB9inrtbldAACKI0ImAKBQXXDBBerWrZvdrrrqKkVFRWXrm5HNArHC23OD73YD4KO6r2d9e/GBFRuyh86qHdW3azMrWX6rr782KTNdPyQftH5WUmw9Z5+Q0rdowyZr21pXqbt9/KpWWJzie64crOcaNs0Kju6IatVGsTKR8vj+fSFGSfPDCrxz/6XPzakDAFCMETIBAIWq0Mpl3ZHKp/o31KZ/jXMn/fECZG6Oa7/ZplI91a3jLgrl+H7lebgA3iREdjMjqu7yPNmh2d1v8J/17OLssTRzy1y9YQJ171/lMvIKAMC5R8gEABSqwi2Xlepe113X1JZ+/M8H+mBPVV0Ua8YOc5G+Uwes4BjVuI1+kcdApirFKa/D+TPXej49f5tqXj/GLpfNvRQ3gH95b+3j2vTW637XkR7S8kWf6Vjrm/W7rmHMwAsAwDlEyAQAFKpCK5f1VG2hNq2sJHh8o5Z8vF51r2xjBTsrpH3wsTMxTvpKvbdsm6/k9cAnS/T5wUpq3OYy5ZUxfcc+tFbr3Yl3Drz7TI5RxlCc0t0IqdRaN93aM+9zBgDgHCNkAgAK1c8//6xDhw7Z7ccff7TLZEP109LS3L3yo6o63NjVHjH8ce16bah7g+52J9yxy0/vnqnPz1yve6ffrrh3J+uh+WYqWiuE/mtctpLWzI3/0qM5Zmw112A+pN80O6Rl05xS1r9svky/C3FNZtWOAzXo2tr68eNp9rYPLa2qds3clXnxP9+DtdR1+APq4XuawD4AAMVXOet/6Gf5J2SURRs3btTcuXP1+OOPu0sAlDTHTp3Q+/tW2Y9jKlVX38ZX2Y8j6fDhw3rxxRfdnnN95unTp1W+fPmgfaN69epWSLzb7UWWuV7yofmp6joma3IexwG9N/l+/V+qE0btCYOAs3T659N6dfMS+3Hl8hXVq14H+zEAlHaETBQIIRMo+YoiZBY3hEwUJUImgLKKclkAAAAAQMQQMgGgtDn0hV74Yz/1GzZNSSnuMtjq3jBeCYmBo5hGXfUdn6gERjFxrvC5BVCKEDIBoBTZOf8B9btvhZr8TxfVcpcBKN743AIobbgmEwVSWNdkZmRk6P3337cnAgEQWnR0tPr27ev2cjr0xQt68O+ndNtfx6hLjLswQFm8JhMoSvm9JjOvz635f+R7773n9oDioWbNmurevbvbAxyMZKLYyMzM1JNPPqldu3a5SwAAAFCcmT98zJkzx+0BDkYyUSCRHsk0AXPSpElq0qSJhg4d6i4FUFCMZALnXqRHMoHiyNzveOLEierQoYNuv/12dynKOkYyUSzs2LFDP/30EwETAACgBDHlsvfdd5+WL1/uLgEImShGoqKi3EcAAAAoKX7++WdVrlzZ7QGETAAAAABABBEyAaAUsW+F0K+f/jgtSYfSvtALf3buu7c13d0AQLHD5xZAacPEPyiQSE/8U1i3RAEQWlFM/HPq1Cnt3LnT7YWnfPnyatSokdsDSq78TvwDlFTff/+9ZsyYoalTp7pLUNYRMlEghEyg5CuKkHno0CFNnjzZ7YWnVq1aGj9+vNsDSi5CJsoKQiYCUS4LAAAAAIgYQiYAoFCZ8temTZvarXHjxqpbt27Iflhlsgfe1ZODB2vY6Fe1wV0kpWvVy2M0bPCf9eziPe4yAABwLhAyAQCFqlq1aho+fLjdzL1wzQ27Q/Vvu+02dy8AAFBSETJxzkyYMMGeTc8089hcl+n1TTN9ACWfuX/awYMH7Xb48OEc/XLlyrlbRlj6SiWMGaxhZtQz28inN+o5Wv9Yby/IOTrq9a029lVvI28/a/mfn9YHZsDUe44cx/YbUQ08j2DP69/8R2jz8RrSV76s+6xtRjy9WHvCeY32oslZx851FPiA3pvsbWfeky+z3otszX2+gNflnFP2Y/iaeS+3Bb6P/tz9vPfckv21AgCKG0ImzqmWLVuqa9euOZoZ+QBQOpw+fVrbtm2z23fffaeTJ09m6xcKE84m/lMVBicqITFRz999rWod+liJvsDox2z71Hx943aN9J3JOug+/nHteif4pG/Rhk3u0uP7dCDVeZgr+zxm6vNjrTVwijmXZ/SbZoe0bJpf+LPUvH5MzvPMz2vIS5DXaALmQ/N3qdXvpljHn6kR11bWpn89m+28HCbk3a//21ZLXcc4r6Hrrrna3HGau19taxtv3XT9vp4VMCdsVjv79Sbqqf7NlLnxLf1r8Un1He+9B9Yuldz35P89oB717CcKjxVgZ878TIfcLgCg+CFk4pwys0j++c9/1siRI33t8ssvV0ZGhrsFgJKuQoUK6tSpk93M57tixYrZ+mfOFHCScytwPecbEbtbsz7zYqGlakcNm2YFnni32yhWJgod378vYOQrXavm/kuf++1qHN+fbIWYSmrc/hdWsFur9SbzbVmvTVZY7Pkrk5DCY+9jHbvmVT3Uo75ZUlddulth0Tr6OnPQoCqpXt06+XgNeQn2Gg/oqw3brKdqrMsuMydWVc3jWwU/rwMr9LW1aVTrHupmn0tdKyxmnVcOdW/QwyY42q/Xeoq4WOu4x7UvrFSeFyvw/i17WAYAFD+ETJxTX3zxhT755BO3Jx05csTum5EPAKVDoZXL1rpe9yY6o2VZI2pZspWC3h88mGRumas3PjumVr1/pUvdZVkqqdEV16lVbRO8vtTW9Zt0qFKcYmuYdceVvM8v6vkCb/aw64TVvP348TT7PO8xI3S1rlL3nk5Cy/s1mFFRZ729r7vUX9DXmL5TB8xpHt+oueNy399/VDc8Xqlu7scNKtsfDnKW76Yt/Zs9otqptwnqAIDiipCJc86EygMHDvger1mzxn4MoHQ4F+Wy5pq9p+dv85WhJjzTP0iIPKTliz7TsdY363dd7eToStcPyVasqlRPdRu2UJtWtfXjf97RW5sOqubl8WoXbGTOF3izh11nFC9v2c7TClr/7+nF+ias1+CVqbrltO7SLCFeY9VGqmtO0ytZtc/daVNvzz5E6Y2ghuvAuy9YQdsKtXYZbqjzCsF7H2ferWtqH9emt173XYdpAvHij8z7MUSDGrvLAADFEiET59zmzZv10Ucf6aefftLixYvdpQBKi0Irl82HAys2BC+xtELWTbf2lFvZ6Tqu/SZk2twy0uN7tPdgLbWNj89X6KraIl5WRrVC6gduWDqgpCWf6ZD1vN2vD1VvGlzI15CXoK+xrq5o08x6qd/q66/zKL6te6UuszbN/HaD/mtvakYqHw9y7WYw6c4IsNs7a1YIHRwQggEAxQ8hE8XCO++8o8TERO3fv99dAqC0MCOXO3bssNv333+vQ4cOhezv3LnT3evsVO04UIOure0rQ31oaVW1y3EpZS11HZ517WAOleJUz1rnC5W1LpeVMX3CujbSXFf5UH9d6itLvV//t6u1Bj6a/Xm987RLYq0g9ecHeurSsF5DXkK/xro3jHIn+xnnPLfdsk9I5KirvqPu1jWVvddwt/51wU0hr8mse8Mf9Ztmx93j3q2EvRerdbip3CuXvXumPrdCfbZzN6Ou992uNm4XAFB8lUtLSyv8PyGj1DG3F5k7d64ef/xxd0n+ebctCcUcu3Xr1m4PQKQdO3VC7+9bZT+OqVRdfRtfZT+OpPT0dL322mtuT/aopQmdF1xwQdC+UbVqVe6XiVLh9M+n9ermJfbjyuUrqle9DvZjoLQxfzCcMWOGpk6d6i5BWUfIRIFEImT6i/TxAOStKEImUJYRMlFWEDIRiHJZAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMFEjr1q31+OOPu72zF+njAQAAADg3CJkAAAAAgIghZAIAAAAAIoaQCQAAAACIGEImCuT4ugSNeWyhdrn9sxXp4wEAAAA4NwiZyBcTBu/ud6ue3lpBsTqqT57op1utcLjPXZ9fkT4eAAAAgHOLkIl8qdR2mGYueFk3ZazQVxuW6ETfBXp9Yh/Vc9fnV6SPBwAAAODcImQiX5yRxzv0dvSVuqJNd1V8LxIjmZE7HgAAAIBzi5CJfHFGHl/XA81PKllVdN2jkRjJjNzxAAAAAJxbhEwUiAmH06ww2NDtn61IHw8AAADAuUHIBAAAAABEDCETAAAAABAxhEwAAAAAQMQQMgEAAAAAEUPIBAAAAABEDCETAAAAABAxhEwAAAAAQMSUS0tLO+M+to14fbLW/LDZ7QFA8TPr1vFqd1FLt4eCOnbqhN7ft8p+HFOpuvo2vsp+DCAyTv98Wq9uXmI/rly+onrV62A/Bkqb77//XjNmzNDUqVPdJSjrgobMmbePV43oau4SACg+Jr/9kq5u0paQGQGETKBwETJRmq1YscIOl8bhw4f11VdfqXv37nbfuPLKK3XxxRe7PZQ1lMsCAAAAyJdPPvlE8+bNs9uSJUvsoOn1TTtw4IC7JcoiQiYAAACAfOvcubNeeumlHC0uLs7dAmUVIRMAAABAvm3atEnJycmKiYnxNTPCuX//fncLlFWETAAAAAD5lpqaaodKz9atW7P1UXYRMgEAAAAUyNKlS7V27Vr7sZn8Z9++ffZjlG2ETAAAAAAF9re//U179uzRO++84y5BWUfIBAAAAFBg5hrMhx56SKdPn3aXoKwjZAIAAADIl+uuu04DBgywm7k/ZoUKFXx90+rWretuibKoXFpa2hn3sW3E65M18/bxqhFdzV2SZdasWdqxY4fbC8/w4cPVtGlTtwcAZ2fy2y/p6iZt1e6ilu4SFNSxUyf0/r5Vbg9AYapcvqJ61evg9oDS5fvvv9eMGTM0depUdwnKOkYyAQAAAAARc45DZorenH2jWj2cvV3/5hp3fWmQ9Rpzvq6jWjH3j6X4tQMAAAAoa/JdLtujRw81adLE7i9fvlzNmjVT7dq1g/bN9qZGO3S5rAlgf9DEH2rrj7fM0ejLvH4ldf31s3qxW0N3uxLq4Nv687N/16dut167v+jj37Zze8Feq1n2gHZfY94LZysA2VEuCwBA8UK5LAIVs3LZGF13aRv3seGN9A3V9K/dRT7eCKG7zgQ6vxFBX5s4Uf+31zrS+tnqZfWzRgoD9jeyHcNdnrFSzzxl9Sf/r1b7bxPYd9sVL72rXWa5JWXtSn1apa+eu97/NTmOrp+vhB+kKhffpod8YTpGvx1OwAQAAABQcuUrZJ46dcoerXzvvffsdvDgwVz7R44ccfcMV4o++WaD9bOymsYUbBSzysV/1AdPvqNNjzyqodXdhTmY8DpOE62Q5+ONOlqh8B9m//tu1tZ33CDpxw6OqqSunXqpvdnnhTXqPtLa3tonyQqTR79/TU8tdWJmzK8madP4P+lyu+fvqDZuWaOd1nE6XtpWJXy8FgAAAAB88hUyy5cvr06dOqlv3752M2WxufWrVctZchvcQf3tn2Yk0JSPmqD4G/UvxNG8o+v/ob+sS3Z7jmzh0SyofZP+nxUQ7cc+bgi+oIWub2FFQ7PNY4/pNxc6ayvF1FcjHdeWgynOgpCO64dD2Z8fAAAAAEqDYlIua67JdEYDvxrUS7W//5t6eOWoNi+EOu2sJsc5uUmz339fBy8eoOEXuct0VN8ezCP0HX1Pvzch+FBf/cMXLLNP3HPFG+9rp71xXirpolqx7mMAAAAAKD2KWbmsVKVpB3UzZa4/7dHOvc6yrBD6T81pG6t9a/6qu5buc9flz76v52nO8cv10A09FOcus55VjWvnEfrsMtq/67FaVth0r/NM+egpDV13RF1//aIvIDdyN8+d93zHtfKbdb5rOAEAAACgpCsm5bJZjm5fpaVpVgy7sIM6umWoOZlrNuu5j/Orkrp2ucNX4uqJubyjOvuHPjPhz4zAazJj1OsqK0j+tFYvfpHzdiTOdZbhiel0k33NqP81nM7I6ANBJjkCAAAAgJKhmJTLZpXDmpLTgxf/UQvuvMFvQhxv/S3uyOHjBZ6BtV67B4PfGqX2TXrWK9U15a+TZqn8dYHXZGaNtO7779v6rNU9euyi41r24V32uY08cKm6+002lPLRI/Zr6vKxmczI2mfNX6z+QN1lQmV0R93/0N/99nde37jzBjG7LAAAAIASK9/3ydyxY4fbC8/w4cNzuU8mAOQP98kEAKB44T6ZCJSvkAkA5xohEwCA4oWQiUDFpFwWAAAAAFAaEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMYRMAAAAAEDEEDIBAAAAABFDyAQAAAAARAwhEwAAAAAQMeXS0tLOuI9tI16frJm3j1eN6GruEgAoPia//ZKubtJW7S5q6S5BOL45sFPpmcfcHoBwNYttpCoVK7s9AMF8//33mjFjhqZOneouQVlHyARQohAyC8b8bq9TrZZiqtRwlwDIy9ItX+nRPn/i9w2QB0ImAhEyAZQohMyC4Xc7kH/8vgHCQ8hEIK7JBAAAAABEDCETAAAAABAxhEwAAAAAQMQQMgEAAAAAEVOkITM9PV2HDh3KVzt16pS7NwAAAACguCvS2WVnzZqlHTt2uL3wDB8+XE2bNnV7AMo6ZnssGGaXBfKP3zdAeJhdFoEolwUAAAAAREyRhsxy5cqpatWqqlWrlt2qVKmiGjVqhOyXL1/e3idPGas1Z+xgDRvs1+55Revc1QCA0LZs2aKVK1fmq5nLHwAAAIIp8nLZHj16qEmTJnZ/+fLlatasmWrXrh20b7bv3r17ruWyGasT9JcXknSwRleNen6I2pqFqQv11Nh52hbVUgMefUg9G9ibAigFKF8rmNx+t3MpAxAcv2+A8FAui0BFOpJ55swZZWZm6tixY3b7+eefdeLEiWz9/ElV0gdWwFQNdRnqBkyjTh/dMaC5lLlZSz5a5xvpHPPKJ1o0JWu0c8wr7lhnjpHQe5TIMCgAAAAA5FuRhsyTJ09q06ZN+vLLL+2WlpamjRs3ZuvnS+oKbdhq/axxueJ9CdNRKS5OZjw0c/8+7XYW6fCyOfrowtFKSJyq/lYGNf1sYdKMhiYmWuuf1+CA4wFAaWUuS2jRooU6duxot8aNG6tNmzYh++ayh7AuZUh9S396+Ea1CmxT/qY17iYAAKD0KdKQecEFF6hdu3bq1q2b3WrWrJmjH2mZ+5KV6j42IfL2ISY91tEV8VbK1GGtX8eQJYCyzVSZmN/BgwYNspv5vdy3b9+Q/bp169r7hKvqJXdqyZPvaNPYYbrGXQYAAEqvEl4um7eoerFWpAQAhGJ+9x44cEC7du2ym/m9nJKSErJvqlLCkb57r36wflavdaFCXhofMNp55f8u1G4la94sv5FPr038i97aG2ofAABQXJTsctlKcYo1CfLwWq0PGJA8vn+/Dlo/o+Lqhf5yoyjF2QcAgLLL/AHQzBZ76NAhu5nf1UeOHAnZP3XqlLtn7o6l7LFDZkgmLM5Yp94j39GmJ9/Rsm6XKf27f+ivy05qwAiz7G/6S0NruwvaaYrZ5rG/6OYLQu1DzAQAoLgo2eWy0e11Qzen7HXF4vd9f8k2M87+dd5Wv/JY1+FletWe7CdVX603F3NGKbYeU88CKNvOP/98e9bv+Ph4u5nbSeXWr1SpkrtnbtL13aED1s/Kal47xlkUqM7N+l8THC90upVj6usiHdPWgynOgmAKsg8AAChSRRoyzUQR/n8Nz8jI0OHDh0P2zV/L85pcok6fcZoxqouiN7+hCe7ssCNfSFJGy0F63LuliadGezXeO93aZqzmb41Si0H3M8EPgDKvcMplj+mHg8nSBS10ffNQf8xL15dz/5hV9jp3ce4jn7aC7AMAAIpSkYZMMyPhokWLNHv2bLt98cUX+te//hWyb8q3ypcv7+4dWnT7YXrGnhU2q816qFeQMtlqumact81LeqCXu0V0ew2dai0LDKUAUAYUSrls6nJ9tMv6WbG+LnJHHQMlf/iUhq1L1/XdZ9mlrysG9tRF7rpQCrIPAAAoWkUaMm+77TaNHz/e1yZOnKhHHnkkZN+0Ro0auXsDAApD5Mtl0/Xlxwv1uSrr+k691M5dmrt0bdy6Np+jkgXZBwAAFLYiDZkAgOLHXJawdetWrVy50m7ff/+9NmzYELJvRj1DX8pgylnHaNi6ZOvxMX28ZISvtLXV1AQreJpN3tVtE/+i5a1H6S8NvW1u1T0HLlX36maD0GJ/nf99AABA0SqXlpaW7WZnI16frJm3j1eN6GruEgAoPia//ZKubtJW7S5q6S5BOHL73f7xxx/b11x6Tp8+rfPOO88XJAP7hpmszdwvMyc3ZG6qryl3Zk3QkyWv9UDxwe8bIDzmj5EzZszQ1KlT3SUo6xjJBIAy7vrrr9egQYN87dZbb9Xvfve7kH3TggdMAEBZdPHFFxMwkQ0hEwAAAAAQMYRMAEAEVdUvB/5Nm/zuZZldXusBAEBJR8gEAAAAAEQMIRMAAABAwe2Yp/vG/Evbsk0nirKMkAkAAAAg/0y47N9Po786owblpLXP/1b9RhM2QcgEAAAAUBBNBujZ+Qt09/kr9fn387W77VwtmP47NQt1K2WUGYRMAAAAAPnnjmTOPN1R11zcXw3WDWQkE7YiDZl79uzRjh078tWOHz/u7g0AAACg2HBHMqdfUU67rWB5+T1vMpIJW7m0tLRsf2sY8fpkzbx9vGpEV3OXRM6sWbPs4Jgfw4cPV9OmTd0egLJu8tsv6eombdXuopbuEoSjMH+3A6UVv28AoGAolwUAAAAAREyRhsxy5cqpfv369sikaXFxcbr44otD9itVqmTvk6fUhXpq8GANC2z3vKJ17iYAAAAAgMJXpCHzzJkzuummm+wSWNOuueYa3XLLLSH7F154ob1PuKJaDtLjiYlKmDpAzdxlAAAAAICiU6Qh8+eff9aRI0d08OBBu508eVJpaWnZ+gWRsTNZB62fUXH11MBZlFPAaOeIp97XbqVq0RS/kU+v3fmUFu8OtQ8AAAAAIJQiDZmnT5/Wrl27tG3bNruZmWN3796drV8Qx/fvt0NmSCYsjv9abScnKiExUU8PaK7MzW/pn+9nqvc4s2yq+je3totqqQFmm5ceUs+oUPsQMwEAAAAglCINmRUqVFDr1q3VqVMnu1WrVi1HP/8ytDPZHsdUXGwdZ1GgOn30kAmO7jBnpbg41Vam9ienOguCKcg+AAAAAFDGlYJy2eNK3m8Fv6hL1OayUMWyGVqdMNZX9jryhaTcRz5tBdkHAMqeLVu2aOXKlflq6enp7t4AAKC0KdL7ZD7//PO65JJLFBMTY/dN4DQzyJoRTq/foUMH1a5d2+6b+2p2797dnmk2JFMKO3aettXoqlHPD1HbIMsaLJyiB+btVItBj+qBXg2UsTpBf7FC4+muozVtiNnDXJs5VvN3ttSAR53Ry9Q89wFwLnDfuoLhHshA/vH75tz5Jnmnfp8w3u0BiLRmsY306rDJbi/yijRkmi8iPXr0UJMmTez+8uXL1axZM1+oDOznHTLNaOMEvZh01BcGbbmGzJruPqmqEXbIDLYPgHOBL30FQ8gE8o/fN+eOCZmvfbVI02990F0CIFKOncjULbPvL9SQWaTlsuael3v27LG/jJiWkpKiH374IWQ/MzMzl/tkegHTXCOZqS1vjPeVtg4zAdNscniZXrjzKa2K/5P6N/e2GaG/72qkX4S4fNNTp0/+9wGAssj8nm7RooU6duxoN3O/4zZt2oTsV61aNbx7IB94T096v9f9272JWu9uAgAAip8iHcl8++23tXfvXrcn/fTTT3aprPdlI7Bv3Hjjjapfv77b8+eGzBUxvtHH7PJaD6AkYmShYArzd3vkq1RcJmTe/6Z2tf6dxj/QU/Xd/jc1u+me5wYr3t0MKCz8vjl3GMkECk+pG8m86aab7BIpr91zzz0aMWJEyL5pwQMmAKC4MLenOnDggH2LKtNOnDhhV6b49wvi6A/JOmT9rBRbTyH/TxAw2jni6cXaowNaONlv5NNrdz6tD8xdqILuAwAAIqVIQyYAoPQ5c+aMHSTNvY5NMzOJB/YL4lhe90A2YfHRTWrn3s/4qd82U+bGf+ufi39Sn/Fm2TPq18zaLqq1Btr3QH5APS4ItQ/3QAYAIFJKcMiMVvthU60vDaFKYfNaDwCIhPLly6thw4Z2SaxpZtbwBg0aZOvn31H94LsHslNmm0PdvnrYBEf3d3xl3/2Mc4mmBdkHAADkCyOZAICzUjjlsseUvN8KflFN1OYXof5SeFSr/j7GV/Y6asanYdzPuCD7AACA/CBkAgDOiimXTU9P16FDh+x28uRJ+77H/v18O/CVNphpwivFKi5Exjzw3vOa9WmGWv5usl36+sLIzgox5ulTkH0AAED+EDIBAGfFlMuamWXj4+PtVqVKlRz9/DmqVe8u1TeKUsue14c5i+xRbVm/MZ+jkgXZBwAA5KVIb2ECAGeLWwoUTGH+bp89e7YaNWqkmJgYu799+3bFxcX5wmVgf+nSperfv7/vlifZmXLWCZr1aR7Rz0zm8+gQnUq8XwvsGyNbixq3V5O01dobP0ZTB5toamaZtdb/YLb1rsN0l4XcB8jC75tzJ7dbmJh7rk+bNs3thcfcrWDMmDFuDyjbiuIWJoRMACUKX/oKpjB/t3/88cf2NZgeUx57/vnn67zznGKZwL7RrVs31a1b1+35c0PmV3F+wdBfXuuByOH3zblDyAQKT6m7TyYAoPS5/vrrNWjQIF/7/e9/r1tuuSVk37TgARMAzq2U5c+oy8M3qpVfG7Rwh7u25Aj2Okzr+uonSnW3saK8/j7Nf/1gPfpl1lrgbBAyAQAAUKJceOGFmjp1qt0mTpyom266KWR/7Nix7l65SdGHiberyzufqd4107XpyXfs9tZVF2vD56MDwlnJ0cZ9LUk3XivnggbXwaUa/8RYTU1prPvvdF7rpvsG6+cvXtHHh9xtgLNAyAQAFCNV1OEP05Tgdy/L7PJaDwAF8N0S/e+Ww1Ld32lSn6zrxZvdMFJjrXSWvPktvfu9syzbKOGkZ/Xx+tf1W99oYFbzgum2d0f5LXdHC78Lvc8Ke3tvVNEJv4H7ZYXegPWuH1N3WWtq6tLa1d0l2W37z1v69zETQkdq6MXuwtrdNHnsfbq+ltsHzkKRhkxTQ79jx458tePHj7t7AwAAALK/H7733nt2+/TTT+3bJuXW/+mnn9w9g9v23xXaaP1s0+wKNXUWuWrooto1rJ8/6tv9qXbA7P/OZzqv5Rh9akYIrz+j2evra7YZCfzTQLW2tox11y27/TodsgLjnT/+xu5venKqFVh/1IKPXtHH1W/VmyH2qWme1nPwa33ygwm/PTX4l3XchVm2vfuE7jHhOJsU7TwUuMzfN/rsG5OYG6tH62ATsAFnr0hD5ttvv61Zs2blq5lgCgAAAHgqVaqkvn372q1z586qVq1arv0LLrjA3bOgftQ3B7/Xum1fWxGusW7vfJ1M5IvpdL/mW8EwZ/xzNLvhBTs4OuvdwJqxWz8csRfkKWXban1uRhxzhF/Ld69r/H/c4dVsDuuHgyZk1lTjuCBndnCXvs1wHwOFhHJZAAAAIFem9PSMG97ywb720SuH/UOQUcdQftSCt4epyzv/VeebEvSGXwmvY7fm/HuuNtbtrdEtzEirHy9E1r1S13qlsP5qN1TjaPcxUEiKNGSWK1fOnkK6adOmdjP3Tbv44otD9s1fqcw+oaVq0ZTBGjb4HiWu8xYt1FODrWX3vCJvEQAAAEqPSJfL1qzT0J4YZ8O2r7TdWeTyHxW82C2dDdc3+nvic/p3uc6acb8pl/27ng8MhCHVVD8rXCbd+At9aoXNwBlukzfP0xwzac//9FNgjvRGP2Nr11PwZ/NKgL/VBxtL3sy5KBmKNGSeOXPGnu1r+PDhdrvmmmvsae1D9c3MYWaf/EhdsV7mHts1Lm+rts4iACilDumLGX9Uv37DNC0p6z6VAIoKn8FzJdLlsjGdbtbtJmUeWKxE3wQ6ZlKdJzTV+qd1JsiJUdtml1lh1C+cffe67gx35lnv+sp88M5rw9p/55j1NdukPT7f6J3ln2Ur6c0pRr/u3MO+FnTD5zM0x1dxa4Xi2c8yuywiokhD5s8//2z/ZengwYN2MzfoTktLy9Y/O6n6av1W62cNxbf1IqY32um1O/X0+7uzr7vzKS12F6UunGJvN+aVTwL2c5vZ9mszWmod560lmjPWW+d/3Kzj5FiXsdpvH9PcUdjA5b6R2AytThibtZ1ZsjpB91vbjHjqLX1or/Pbz25+I7sASqedC/Rgv/u04pLf6DpmAgSKHp/BUuZS/WGMGWk8Y5epZpW3lrNHFL1yVXMN5t/c25rY27y+TwP6hgpz1jH/Z6BaZ3yqkc9Y2z6bqEMN22S/lUieLtW1l1pJ0jrG35ZnjTqaiYJm5iih/U5/n2ZuS2Ief6tnXvLKdG+0b81iFidvnqbO0/+l7Zfcqjfvu1f/U9l/u0n6/vIhzC6LiChnhbxsQ4UjXp+smbePV43oau6SyHnhhRfUokULxcbG2v0DBw6oevXqqlixoq/frl071a5d2+6biX+6d+9ul84GZ0LiWM3fWkNdRj+v/qcT9JcXkpTRcpDGPdRLDQLWD25rAtsEvZh0VC0GPaoHekU563e21IBHH1LPBk44fGDeVtXoOlrThpig6h7Dbxu7JHfsPG1TlHOczsmaM+EFfXbU2abD+ima8PXl2c/B27+mFSbNtqe6atTzQ5zRVhMw/Ze5x//Bfh2dlWyf8yn3NTghM/vr9F5X1jZAaTX57Zd0dZO2andRS3dJ8bN//377D2eRYi4jiI4OcQHNoS8048G/6+Rtf9WYLqG/uhTm73agtArr900Yn8Hvv/9eGRlFN9PKeeedp5Yti+/vyHB8k7xTr321SNNvfdBdksVMCjlt2jS3Fx5zudaYMWPcXmn1jRMyy/1O74z+Xc6JgvJcj7Li2IlM3TL7fr06bLK7JPKKdCSzfPnyatKkieLj4+1WpUqVHP2COayk6YM1MlvwsqSu0IatUlTLnrreDl7Ran9jNzVTpr5f/7Wyxh0LJqrlzbqll/VM0S3UpnUdKfM7bfh6t+r0GadZ3jmokmLNzF6Z+5QcopYiY8t6bbLW+Up861ypNs3N4dbrv2d7kgCK1ObNm/XII49o7ty5EWspKZThASXZsmXLgn62C6tNnz5dc+bMcZ+99DGBcerUqflqpT9gAsVLkY5kzpw5U1dffbUuuugiu79x40Y1aNDAHs30+q1bty7wSObgBu4IYw1nRPDSHCN+Zhf/UcKO2mDvbx8sm3BGMp1j+I8kuiOk3shmtlDpnuOlOUcyvdHTHKLMc45UzBJz7JwJNYqRTJRBxXkk0wRM82Vm7NixRTeKUAxGMgsySpPr6CxQTERqJLOo/fjjj5o4caIuv/xyDR061F1asuQ2kolQGMlEeErdSObp06e1a9cubdu2zW5mZrDdu3dn65+VOtfp113qSIeXa8n7uxXdKFZOXM2DCXOTE5WQmKinBzR3FxZElGLrRWnR827prH3MWbrLnFMuKsXF2edpgq05B197yQ21NhNSneUzRnUJ73UBKFL/+te/NGTIkBJfppZfJmRu2rQpX60oSwfPxomdX2jBnNe0ZOOP7hKcS+kbFimRf4881axZU4899pg9syrKEnNd6TvaFDJA5rUeiJwiDZkVKlSwRyo7depkNzPzV2D/7ESrRXxrK4Blasvij7TOKzvdvFgf2xPhZGj1O0u1zQpsV/b0ylkLLnPzW/qnmdAnY4s2bEy1MmY9xQbmSW9dLqJbxKuVycZr13HbFaCEM1/uECHpG/T+nDlWqAho85af9eUO4UnXto3bdLRCjOpfaP27ntipL960nv+1D5Qt43jnWWTnVXZVvaSB6uqkUnfvVT7vVljm8LsIwLlUpCHT3PPSXKy9Y8cOu5nrjH744YeQ/czMzDzuk5lTdPsb1dUMRh5eq/Xr6qj3PaN0bR3nms1hg0dEtKQ0qnFrlf9ovIaNMKWxNdRluBl5tJ7zTwPULHOz5o23nnPE/2p3o8tyH3mMbq+hD1v7HF6mF/xmiR3x1Pt8YQFQ7Jnf06b8tVWrVnYzt5+69NJLQ/ZNmWx+frdXuPAK3TR0qAb3b28FjCKU/p12J1vPH9NA9UN+X0/X15+t1gG3h0JW9RI1iJVOpuzWHgYzAaDYKtJrMt9++23t3bvX7Vn/kzh5Uueff749C1qwvnHjjTfaF3gXKzmuyQRQVIrzNZkTJkzQwIED7QqNQmdunzDmnwE3Da+ubmOe1l1X5yzRL8zf7Z988on9mmNinOvRvv32W3sWce+ay8C+2d6Ezbp1c4+MplT1vaXb9HOLX+u3nazftGbEcL4V6KJb6PoBnZzfvd4yew8nkPbucZF2LZqvNVZAzKbCherQp4dalw+2T2sF3rQ8x/Obkcx3lmr7Cfc4NU9o5xfv6JNtR50d3POKyXM/++DOMndXm3d+wdb7vWZTMvp/qw+p3hV91L11ZfccTrj9mu5698X7v1c+fuft/5x+72Vl79z9t7VFq/mvB+iX3gGzvf9Z67Kdg62Ce37l9bX5tzkU+B5mnX/uz+mtO5P9PApJrr9v8vkZPBf69eunBQsWuL2ShWsygcJT6q7JvOmmmzR8+HBfGzVqlO66666QfdOKXcAEgOKgUT/91fryaL5AZrWEc/Ll1twD2Uw0kpycbLeffvopR78gfkpLk38Gy8EEnLf36aKbh2rw0KH6TftYndy7Vl9tPKXLeptl/dXO3DHLBCmzzW1WqDEBM+g+OYfFnOevoOrVgk9QdGLnKq2yglCFmjWV77nRf0rTETvjmVFa9zw9XsA8YwVEbwQ3Y4s+/WBjzhLRE/u1e691oOgmauUXME1ItF9fix+1fHlgTcxPOpLmvrMnU7Rnr/Pa07/b7QveJ4+kWc/lH+i89zNDWz9xy4X9Q799ni3043+W61srZC/xPwfrPQ6f85xfndfJ3nfwLd3UtIr1nNZxnVdRUbWqmn8P8xrO8VBmMfoMAkBxU6QhEwBQ+pjSV3OLqgsuuMBupholsJ9/J3Qo3UwOFDrkqWob9TLB0S1lvaB6dSvsnVTakVwmFQp7H+/5L1C16u7G/n7aqVVfbdNRK2B1vr6xKruLw3XiULqOWT8rVKuecwR1/27ttzJg5YYNnRHIXEpEs2+bru/t+t4L1aqFM8RXtU1vd0TSz4lDsl9udCNdFOtd3+jsW7npZVaoczbLCrDWsZ0T0cXOidjB1AmlFVSvdQv3PK331ozk5vXHgVxVVKOrf5t1zhVryf7n/+mIvEwZ1r8zAOCcImQWRJ0+eigx0e9emABQdpmQWbVqVXuiEdNMwAzs55872uZNuhOUGfV60zch0BtLrdDnrgmtIPsEOqkD67/S9qPRan5VYClqlmNbPnSe558BZbGW3EZJvRFc3/5zgpT+Wuew76u3rPP/TlWvuNkty3XDY5gqVI9VMys02uF1t7n+1Dqfqk5cPpl2REfd0VYzgd3H7vuVVQL7kxvCczLB1oxeeuefvWw2DGaE1H2+4K8dAFDcETIBAGelUMpl3Ul3dEE1BRtINNI3fOxey3ezXVo5qFuzPMtWC7JPDidT9MOeo6rc4qpcrwn0ykWdkk93oc0dJQ0RoJ2ROr/9veY3AmvtbL+GQd0uUboVNt80JbHeqF9evFLdatVV38zWar2e7au26oA5n0YNs0YOj1VXNXMiXjmsr92m7q1j3bLVIE7s1Iat1j+eW6acr3JZUyq82K8EN7CUGABQIhAyAQDFzAnt3GCFHv9SzDyd0P7de/M5KpnbPnlc+2eFoE6BZajhSt+qTeZazhCz1laMa6A4K9wd27UrzxnGKzZqo2ZWCDu2Y6M2/pi9nNUwkxctDLgm0yvVtdmluCd1+EfvfEx5sJuIL4hTgwutxxnWeQQ5kRy3EzEB8b3l+tYt4c19Vt4weX9s8JPXtbIAgHOPkAkAOCvmmktTFmtmkDXNXIcZ2A+fN9mMiX5OSahTNmk1bxZTU7752gf6oeG1amcFJGebf+qLH2vLZKLcVG0T/j4hr/0zI3S/Dl0mm6uMrNlYT+79Sm/7l4Se3KtVb83TlymNdHVPZ7Ifr0zVtH8Gm/jHd53kXm3astt6fdfrumYVfe/bGyvOU3zQMOyFNC9UVlCdBhdmXR96Mk3pGeb6yJ7OZD8fZp2H7z6hVduoW7dmqui9jn+u0Pltf6EMc2/RwOMFsl+rOd4/s/1bv7nmfHW4opmqeK99/hZFNfIfyszjWlkAQLFQpLcwAYCzxS1MCqYwf7cnJSWpcuXKdjMOHz5s366kQoUKQfs7d+5Ux44dfbc8yc4Nmd9Vy7q1RjZ5rY8gd/bUH0Pc4qRA3GMe9d0iJIszM+zRIrk1R3GT43YxIaUH3ALFXVxIivPvm3BwCxMAwZS6W5gAAEqfRo0a+QKmUa1aNV+gNAL7gdsXW9z4v/hxy2cjUooLACg0hEwAwFm5+OKL7dFbr1122WW59k0zI5vFX1U1a91MVdxSVJx7zm1TotXY+m8oIiPLAIBCQcgEABQjzn0Ss8+k6i+v9ZFVsdHV6jd0aB4lnPlg7iUZ4njm1h+Dh5a9Ulkj3Pe5LL9HAFCSEDIBAABQZpjbLh06dChfzVxbDiB8RTrxz5YtW5Senu72wtOiRQv7pt4AYDDxT8EwqRuQf0z8c+4U5sQ/e/bs0bRp09xeeOrXr68xY8a4PaBkK3UT/yxdulRvvPFGvpq5kTcAAAAAoGSgXBYAAABlRqVKlez7+9aqVctu5r6+VapUCdmvUaOGjh8/7u6du+3zxmnY4ME52oT537pbAGVDkYbMcuXK2eWv5v5oppkZCdu0aROyb8pkzT6hpWrRFPPhvUeJ69xFlozVCbrf+kCPeOp9MR8gAAAAPCYw1qtXT+PHj7fbqFGjdP3114fs/+EPf7CDafiqqcMdU5WQmKhxfeq7y4CypUhD5pkzZ9StWzcNGjTIbh06dFDfvn1D9uvWrWvvAwAAAESK+X557Ngxu506dUo//fRTtr5p+ZeivclHrJ/VVbd+HWdRENlHO0dq1mepZqEe9S3LavfO/EwHQ+0DFGNFGjJPnz6tAwcOaNeuXXY7ceKEUlJSsvULR4ZWJ4z1+3D6jXxmrNacsd5yv9FPb/k9r8jZ1DvGnXr6fXd8NHWhnvIdM2vf1IVT7P6YV9w9c4yshj4fb1tvX9953PmUFls751gfbDQ3xHkF8s4zsPlvn3Mbv9cf8N4571Xga/Oae34hzi3wPQp8nYH97Ofld04AAAB5MKOZX375pd3WrFljfwf17xdMmpL35T7BpQmLMw/00jOJiUpIfFS96h/Rqnlv6LMaA/SEWfZoH5mxz2od77C3ee7ua/VjqH3ImSjGinwk03yIzQfbNDOFdGA/8kzomaDXz/u9XbaQMGuUrq1zWElzTCCyAtrsD1VvtPnQztJdXeooc/Nb+mc4gcWEpfFfq+1ks2+inh7QPMx9nfN5MemUutjPO1X9m1vnM9sJkfljjvWk5m91u4Y5r7Hz9EPLQXrcOq8Zo7ooevMbmuYLpYGi1GLQZPs1mG1ru0sdGdqZbP5+VsM6V+f98TEBc8KrOu/3zuu39z28TK++8o3aDzMlIt72Zl+zzfMa3CD0uUW3v1Fdm0uZ363Xf3O8D6lK+iBJB61jxbdtawfMCV9fbh/Def8yteWt1wrw/gEAgLKocuXKdnWdaVdccYV9iZZ/v3z58u6W+ZCyR/ZAZrU4xYaYyLvpgCl2cHS+b1VXbL2q0pH9zn4hFGQf4Fwr0pBpPrANGzZUs2bN7Gbq2xs0aJCtXzBWSJueNTo28gUTSDzRduiZNqSt222kWPMpzdyv/bvrqPd9D6lntps6R1kf3jDu8lynjx56KWvfSnFx1oc/U/uT8/izUsYWbdhobVPjciswmQV1dEW8na604ev8paSM1XP1RlL250tdsV7brNdwcfxlMqcW3SJeraysd3jtOndEtgCi6ik2sOojur2GTrWCo+9tjbV/+WXu3xd01NTI/dxyeR9SV2iDFaSjWvbU9dbz1ekzTrMe6mUfw3rnFRtnHSRzn/J66wEAAIxCKZdNS1ZyupUxmzvfb4JKSdLMu73vrPfplVVh3NqvIPsA51gpKZf1Rsv8RtXcNbZsJZpjs4/8+Uo+R+hFK7DV6DrUF5xsh5fpBXs/Z32W7GWh/sHWCZwhHN/vhCHfcQfrgXn+J+Q4vGy6c+wRLwQvhzixVfP+maSMlr3VzcpmDm/kMVNb3hif+/5hOa7k/dbOUXGKC5K7s5Wsjp1nBcjc5H1uJjw+PaCRvd57P+33wR39HOcFy2xluoH/LgCK2scffxz0FlS5NfP/AgA4VwqjXHb7mnXaY/2sFlc/xPfA7XpzeoLWlOuooVPNd9ZnNaRDXveCL8g+wLlX5OWy6enpOnTokN1OnjypI0eOZOtHnAkkT1oBqEZXjfKVV7rrDHtEzgmnpuTVhJqs6x0tvv2yl4umLnzeCjdHg5aaRrcfqEHWtl5QzDayWinOGRX0HddrL+mBXllJrkbX0c5yu7zXXejn8H8W6bOjLXXjbderlrvMemY1sodps0pgfe35IfLPzmFxRxBrXN42x77mGsm/WuHYd55TB6iZuy64vM7NCe0PzEu2/2DgvZ/28a1jX7T5DU2wr/lM1aLnrXBqvfYBdqlyQBkvgCK3detWrVy5Ml/N/O4vCY6u+rvuH3ynnilJ9fgH3tOT1v97Rjy92P7CCyCniJfLpiRp8afWJ65aR/36usbuwjykbLK+Z+VzVLIg+wDnQJGXyzZp0kTx8fF2M/cgCuwXOjc4OazA8mxBroUMlKEt6zfmKNH1QlS2kdXoFmrT2gpFh9dqfYHrVw0rrN18W0Cpr1Tnyngr7GXq+/VfhyxbDZdT3upcB5kXZ9vc5XpuqZ/oQzMi6Ssj9lPnOv3aBMlg75lXfgyg9HHDkq9iwmv3Jmq9u0nhOqCkDz7VwagmavML88v2gBZO9s4jSPA8ukoJY7z19+ofRXOSOdW9Qm2aSZk7NgS5xh2AuTwrIyPDN8hx+PBhu0w2VN+bPyQkU876WILWmOx3ZGW2SRGnLHT+1LP73cd078x96jasj+p729w3XxnNmiv3ccmm+m2+9wHOvSINmeael/5/8f7++++1YcOGkH0z6pn7fTLDEN1eA25xJqWxy1PHLlGV9t5QZh31HnKZ1o13fhGYstWoloM0xrt+Mxd1+vzJmXDGLv0cob/vaqRfhDWgZgLow85kP37XkXqzx4arRtfh2UY+fer00Uh3Qp0J3rGtlm10Ngw/LpxivR871WLQ/dnLh12Bo7UPLKmidv4jxMHkcm7e9Zotev4qyIhrtFrEt7aC+mGtWLxSbf40QM0yN2ue+Xcb8b/a3eiyEGUpAIqC+T1t7ikX6nZUwW5PlZ/f7VGtf+fMuvjMb3Wpu6xIHPhKG7ZZz9+kjeyMefQH2VX/UfV1Ye1MbV78cbawe+CTD/R5hlnnLjhn6qpjvJ0ytYGUCeRw3nnn2W327Nl2e/XVV7VixYqQ/X/+85+qXr26u3do3oyw2aq1THt2mNp5qbCpO4us3WbowVHj9HziJPX3Bj/d9VkT/Vjy2gcohsqlpaVluxHliNcna+bt41UjOsS0WGfBXLdjrsH0mPLY888/3/6gB+sbpmzBfCEBAGPy2y/p6iZt1e6ilu6S4mPChAkaOHCgWrdu7S4pPgrzd/usWbPUo0cPuzLFWL58uT2ZW+3azlekwL7Zvnv37mratKndD8WUqj4241P93G2Mpg6Od0Y2739T39TspnueGyxrSdYyew8nkI5/oJ3WTb5fCwLLK6Jaa+CjD6jHBcH26WnfNsBfjuc3I5UTZlhBsrV6XnNSiz9KUdcxz+n3zoloofWcCyv01lUnF2nptppZ64Keo/d8R7Xq7xM061OnFsa3znuurBIZyX3dTcJ4X3KcOwqkOP++CUe/fv20YMECt1eyfJO8U699tUjTb33QXVKMuSOZ21vcoUf9w6Enr/VAETt2IlO3zL5frw6b7C6JvCIdyfT/S7dpv//973XLLbeE7JtGwASA4s3Mwrhjxw6tX7/ebkePHs3RL4hj+/f7XYYQhAlXj25SO/dWUk/9tpkyN/5b/1z8k/qMN8ueUT9zsbgJl2abl9yAGXSfnCN+zvNHKc6+njy76vHxulQ/at06dyzTHvWM0iVtWqqms8ThBsBd7mjsCyM7K3rjvzQt0eznBcwMtfyduVb9RQ2r/al1Lhu08HknzNrn/eJIXZPPb6VVLoq1r9c/nryP6zIBAEWuSEMmAKD0MdUnMTEx9i2pTKtYsaLq1KmTrZ9/R/WDU5saNOTZ6vbVwyY4ulcOVPbdSiqXaBr2Pt7zV1JcsNta1XKue/xx7TpZMVqr3l2qb+xrN+PcDRwHvlqvb6zXcEmbX9gjl1VaxKul9XLs/Y6aa8qt56h5lbrbF9hXUYc/TNH91/zklOWejcpx9u26Mvcmi6vWgUIW00V3zwwocfWX13qgFCJkAgDOigmZ1apVs8thTatQoYJ9/ZJ/P/+OKXm/lbR8k+4EY0YCx/iu7x4149PcRz5tBdknGPe6xx//oyVv/ccOi75rN328oJqpzf9yb910l18J7LH9wcNklQ4a9vhIXRO9UXPNtef++wAAUAIQMgEAZ6VQymXdSXdUKTbofXqNA+8971dq6pSi5jVKUJB9Qql7hSmZtQLkv1+3QmDWaGWWKrrIvXWT93y+Zq6ddEcbg7EnEbKCZc1uYwpULgsAwLlEyAQAnBUzU6y5x1ytWrXsZkYuzcimfz9/3PJTE856Xu9M8JOnowG3kgpHbvt4AfG49u8LMUOre6sQW4gRVy+IfrfhvzmvjaxibmllPcePa7XBu7TzvWf0zOINWrneJOyaatu2gJP2uKOkURfGijsJAwCKGiETAHBWzKzgZpK2hg0b2s1cg2mu0fTvh8+bDMdEP78yU9O8GVp/XKrn73xaa9v+Uf2aedvcpYTdF8tkttzU7Rv+Pnlf4+mWzFpylsq66vbVSHeyn0e912G1sfbEP+YazIes8/lRy6Y5y/+y6TLdXGelPrEz5uVqk0vG/HHpNOd4Ae/LB1YmPvpDsg5ZiyrF1ssxay4AAIWtSG9hAgBni1uYFExh/m4395ErX768PZppmFtVmZFML1wG9rds2WLPJu7d8iQ7N2R+FefcbiRHcMtrfQT5zQwb7BYnxYtzC5UFPzi3abl83WQ99OYPavm7R3W/PakQCoJbmJw7JeoWJkAJU+puYQIAKH26du2qtm3b2qHRtF/+8pdq1apVyH6fPn1Kxu2p3HLYzB0b9N8QFbPF0wGn3DbXSZMAACg8hEwAwFlp0aKFOnbsmK/mjXoWb3XVpUdn1c7cqCUfuxdNlgSHnEmTal7Vo3BHegEACIGQCQAoRsx1itOU4Hcvy+zyWh9ZVTr8Qc8kJmrq4AJOwFNk6qrP+ETnfWnTVw+XiHMGAJRWhEwAAACUGd5tl/LTdu7c6e4NIBxFOvHPypUrdeiQme8ufKasykyBDwAGE/8UTGH+bgdKKyb+OXcKc+KfPXv2aNq0aW4vPPXr19eYMWPcHlCylbqJf0zIXLJkSb5afkMpAABAWfT9999r2bJlvmb49816ACgKpaNcNnWhnvK7/9iwO5/S4hI1EyAAAMDZ+eqrrzRz5kxfM/z7Zj2kSpUq2bddatq0qd0aN25sz3gdqt+oUSMdP37c3Tt32+eNy/o+arV7Z36mUHfaBUqzIg2Z5cqVs8tfu3fvbjczpf21114bsm/KZM0+uclYnaD7x87TthpdNSoxUQlWm/Gnuvr8tfdFzgQAAGWJKet84okncrRf/OIX7hYwgTE2NlbDhw+3m7lvb6dOnUL2+/fvbwfT3KXo0xl3a8rCPWpww0T7+2hC4rP6zZn3NfezVHcboOwo0pB55swZO2T26NHDbl6oDNWvWbOmvU9oqUr6IEkHVUNdhg5RW3dpdPthmvRQR22YYv6KdI8S17krrO0XmWX2SKf72Pyl6Z5X5G1ih1b7r0936un3nZiaunCK+xcpv2NlrNacsc7+I57KCrRZ22Y/BgAAQGHbv3+/fvzxR/vacK+Z/ubNm90tYJjJfw4ePGi3o0eP6sSJE9n6Zn2+bF+mD1elSw1v0JD+jd2FMeo8copG1FuqR833wkfm61t3jbbPs5fZI53uY/PdccJ8bwsntNrfJ0fOlJNTt+vNcc52/sdKSZqhe+z9R2qWL9D6bZvtGEDRKNKQaT6wu3bt0rZt2+xm/pK0e/fubP18SV2hDVutnzUuV7yXMH3q6Ir45tbPw1q/zk2G7vZRl8TrFzV3KtmrXzi81trGPMjQlvUb3bKGTO1PNp/GDO3M2tB3rIwt67XJ/bBm7ku24qsTMCd8fbket/96NVX9m2dqy1uvUboLAACKxOnTp/XJJ5/oyJEjdt/8NH2zHFlOnjzp+/753Xff5ejn1/Y167TH+tmgbTt5EdOnaTu1qW/93LVOa9xk6GxfTc3iW+rnPcly/rWk3evWOOExZZP1ndUKrcaR/Uo2G6TscX4avmOlaLP15dbZ8oj13dVsYALm80rpNdUZUX20j+ofWakFb1C6i6Jzzq/JrFixol2CYNp55+XvdDJ2Juf6YalzXQ9dW8dkyHX2SGXqivXapihdHH+ZGhy3PrBWMoxq3F6/qOOGx4wt2rDxqFr0/pWaOYewHFfyfntDtbusjnssJ4xmtOytbibHuur0GadZD/WSc+u2SoqNs548c5/9PAAAAEVhzZo1vol/Nm7caPeRnfneaUpiTbvssstUpUqVbH1zzWb4UrTXl/6CaarrenRQVe3SBjsZbtfadVYkrdZcl7Wso7TkfVZIrKbm7ZurqhseUzZt0DflOqpnF5NOXWnJSrbSZLUW7dWsqnssO4yWU4feXZS1ZVP9dsoMjTBfgo3qsYqtarJqstKcJUChK9KQaT6wDRs2VLNmzexmPuAxMTH2MtNM4MyP6Eaxqu0+Diq6hdq0tlOmFSJT9dV6exhTbS7LuoN3VKOO6mJtY8Ljl/boZJRiY51bpmTu35d1XWdUI3Xo2lq1zbGWmzCaqqi4WNlbZu7XfrOhXwntsMEj9GIS6RIAABS9+fPn26Wf//jHP9wl8BfZctkYXRib++2hYlq10aVW0LNHKrev0QY7Y8arlZsDrSSoJldfbW1jwuNqZ3Syepxiq5h1aTqwJ+s7ZbVLr9ZVzavax1pjwmh6ddV1NrSC5B57ACarhNZq9yVojTsoChSVkl0uW8n68JkPp6/cNVC0WsRbwVCHtWLeNC3zSmWtjOmMgkYpLrahs83h5XpvwUYdNKW3HZ3j2mWwGU5ZbVS9WDVoYX4ZWMd6d4EVRmsovm1Hv9HKVC16/gV9drSlBkw25bKzdFcX328OAACAIpORkaGHHnrIvkYTOUW6XLZ6bD1ZGTKr3DVQTCu1sYKhdiUpIeFTX6lsbW8UtJr13bORs83upAVasjXdLr1tZR/XKYNNsctqq1nfXRupZRsz6pmk//vACqMN26pda7/Ryu3z9ELCKpXreIeeMeWyzw5TO3NyQBE65+WyZyW6vW6w61UPK2lO1uQ95pYm09zJeKLb36iu1iaZe8xfdmroyp5OOetx65euV2obbYfHTO3dk6oal7dV2+hGivWGSN2yWps7Mmofy74ONFqNfBsGsEtvGckEAABFw9xqo1u3br5m7jXu3zfr4YhsuayVIbv00jX2dZfv6hXf5D3S9nlT3Ml4YtS5V2fVt2Li3j1mgqAu6mmXs6YpeZ83zBjjhMcje7Q3vaHatGusmPqxVqx0OGW1Dmdk1DmWfR1oTH2FGky1S28ZyUQRO+flsg0aNMjWzy9zHeSMUV1U+/AyveCVBYz/Wq1u866N9CYAsuSYIChKsfWsrXyh0oxO+m1gymD3OQ+j4upZx8sKlXYYtR8ZmdYviEz1/tMANcvcrHnjrXMY8b/a3eiy3Mt5AQAAIuTKK6/UXXfd5Wtmhn7/vlkPJ2CaCZF27Nhht507d9plsqH6ycnJYVTbmesgn9WQDlW1+93H3EunBmvmgWs10Ls20psAyJJjgqDqcapvbeYLlWZ00m8DUwbrXE9ZXXWdDd1Q6YRRn7T92lNjgAb3seLsypftOyY8OP+oLjWjqEARKpeWlpbtHiEjXp+smbePV43o3GvLC2L27Nn2bUlMM0ypbO3atX3hMrC/atUqDRo0SE2aNLH7BWVuS/KXF5J0uutoTRuSYxpaACXI5Ldf0tVNrP/5XtTSXVJ8TJgwQQMHDrRvGVDcFObvdqC0Ks6/b8LRr18/LViwwO2VLN8k79RrXy3S9FsfdJdETnp6ul577TW359xiz5TLXnDBBUH7RtWqVXXbbbe5vYIytyV5TK+sqqHeEyfJd6cToIgdO5GpW2bfr1eHTXaXRF6RjmR26NDBFzCNuLg4RUVFub2c/cDtC8a7LYm5/pJrJAEAAMoyExiHDx/uayNGjNA999wTsm/a2QdMi3dbEnP9JX/vQylXpCGzY8eO6tGjh6/16dNHPXv2DNk3rVYtZ6bXAvOujQyYVRYAAAAoKt61kdlnlQVKp5I98U84ottr6NREJbz0kHqSMQEAAHAOxHQZqecTE/Xc3dcyZwdKvdIfMgEAAAAARYaQCQAAAACIGEImAAAAACBiCJkAAAAAgIgp0vtkAsDZ4j6ZBWN+tz/Y9w9qWCvOXQIgL395a7Zujr+O+2SeA4V5n0ygrCuK+2QSMgGUKITMgnnu49e0bf9OtwcgXKN/fZsurdvI7ZUshEwAwRAyASAAIRMAwkPIBBBMUYRMrskEgAL66aeflJKS4msnT57U4cOHff0ff/zR3RIAAKDsIGQCQAF98803+vOf/+xr27Zt07Rp03z96dOnu1sCAIqLU6dOaceOHflqO3dyuQGQH0VaLvvxxx/bf93Pj27duqlu3bpuD0BZV5zKZTdu3KhJkybpxhtv1Pnnn+8udfzwww86cuSIHn/8cXcJABQtymWD27Nnj/0HwfyoX7++xowZ4/aAkq3Ulctu3bpVK1euzFczX9KKpwytThirYYMHO+2eV7TOXQOg7DAls7Vq1bKvxfRa9+7ddezYMXcLAACAsqV0lMumLtRTXtgz7c6ntHi3u64QpC6cYj3PCL2YlOouibAifj0Azs4nn3yiffv2uT2nv379ercHAChOKlWqpPLly6tp06Z2a9y4sV01F6rfqFEjHT9+3N07hO3z9Kj5zvbIfH3rWzTO/h43Yb63BCg7ijRklitXTtdff70GDRpktw4dOqhv374h++YDbvbJTcbqBN0/dp621eiqUYmJSrDajD/V1eevva9CyWUZq/Xu0q2S3/PZ7fkhautuclZMwLRezw8tB+lx79gvPaSeDdz1AIodcy2mCZbGt99+q6SkJPsxAKD4MYExNjZWw4cPt9vvf/97derUKWS/f//+djDNn+1au26P9bOh2rRr7CwCypAiDZlnzpxR8+bN1bFjR7tdfPHFatOmTch+1apV7X1CS1XSB0k6qBrqMjQr5EW3H6ZJI+vqw7F+o4Fec8tandHIrOUjnvIPpQGlsHa7R4nWjhlb1mtTapRaXHW+Fges89jB12/fMa+4K62AOseck6+0NlWLpvjvbz3vO0u1Laqlbrytl8iVQMnxf//3f9q/f79d5m+uxwQAFF9m8p+DBw/a7ejRozpx4kS2vll/Vrav0QY7Y7aVL2N6o51eGzlTn/kVxaUkzdA9/uutdu/Mz6zvucGk6NMZd/ttt1AL/fpZ7RHZA6kpSZp5t99ye8Q1+zGymrXPand7v5HZLN5+7rGNICO5KNuKNGR6s3mZMjLTzIc4sJ8vqSu0Yav1s8blig8cRoxur6FTE5Uwa5SurWP1vZHH54eogRUwH5i31Vo02hn5HNVF0Zvf0BRf0Dyu5P3Wp94KewMmT1X/5vZC23HrS+RBZWrL0j1qO9k7/mElzXZKWk3A/MsLSTrtHvvpAc11eNlsPf1+GOOqGVu0YaP5bXNEn0/3PuiBARhAcXT69GnNmDFD//73v90lAIDiyvzO3r17t93M5Q6B/bNjhbD3P9UeVVOHHtfJzpgmhD2xUHsa3qBHzPfRZ4ep3ZmVmvNYVtBMS96ndLPPHVOV8Ggf1XcWB2FC3mN6ZVU5Z9vEZ/WbM19oZ9u/2I+HdKhqbdNQvSdaz5M4Sf2rWoHxsQ8VN8b0E/XXYR1Udde7emV+ujpbQTfoPhfZTxQeE2Cfs16b2wWMIi+XNaOTZpIM0ypUqKBq1apl6+dHxs7kEH/dyU2qvlpvJVMrQHb/lZNMo9vfqK5WkMz8br3+65/mouIUF3Q4MUotbr7NKWGNbqE2ra0Um7lPyakZ2rJ+oz2yGt/WOXadK+PVzAql36//Oh9BsZquGW0+5LN0V5c6ytz8lv4ZTkgFUKTM7yxT1u8180ez6OhoX79mzZrulgCA4qRixYqKj4+326WXXqrKlStn65trNgvECm+TBt/nBsCJGmGPdJiBzXXZQ2dMF/XsbMXII1v19WaTMlO0N9lMdllddes7+4SUskkbtqZbmdA6hn38GCssTvE9Vw7Wc9090wqO7ohqTP1Y60ysp96/pwDfowNZgfeNN7XGOh3AX5GGTDPFv/ni1bBhQ7uZD3hMTEy2fn5EN4pVbfdx2DJ2KjmvT5S7TVS9WOXxMfeTqeR93zojoDqsJG8k0lwv6mxQANFqEd/aeo2Z2p/s/pkLQLHRrFkzzZ4929fMF5PRo0f7+uYxAKD4KbRyWXekclyfqlr18lh30h8vQOYmzfoeaSW1anGKzesugmnJSs5nqPMmIbKbGVF1l+fJDs3ufoNHapZ/fa/l6Mo3tMAE6t5dchl5RVlUsstlK1kfRJMCD6/Ver9rInMV3UixeSRT77rLi+Mvy3FdZKW4uBChL0qx9RorNs6cUA11sUcis9qsh7jGEgAAoDg4efKkPWmbad99912O/tlq2rWH2lWVdict0mepMbowr+SYskcmh1ZrHq9WeY1wVI9VrKluDZO51nPGwj1qcMNE53tprqW4AfzLe6se0ap5b/hdR7pLny5apXIdB2hg+yruMsBRostlzXWXN3QzF0weVtIcv/tUpi7UtJDXMdbRFfGmNnazlnzk7JGx+h0tMxPGduqpng3ckteoS9TmspyxMLqF8+E/vHad83ypn+jDpFRFteyp69t6I4+HrdAbbur14yu9/U4bvjZnnzWxkVd+CwAAgLNjZos1M8iadtlll6lKlSrZ+gUul/XEtFKb5lYSPLJSH37yrZq2a2sFOyukffCJMzFOSpIWf7rHV/K6fdkHWpNeTc3iW+Zdpecde9c6rXFn2dk+b0qOUcZQnNLdCKnWUf0GXZv/ykKUeiW6XNao02ecPXFP7cPL9II3nD/+a7XKZXbWOn3usa91PLxsur39SHeinmlDLtXqhAl6MemUugwPcdsQM6HQwwPUzHs+93Yj49yRSjOz7YP2ZD/OsZ12Z/aJf3znOlbzzcRFdnmt2eZHtR/2sPo3z9SWN8a7682o6PMaTMYEAAA4ayZgHjlyxK6mM23nzp12mWyofnJyct73ycwhRp17dbZHDHevW6Nvmw7QKHfCHbv89L4Eralxgx6Z1F8/zxunKQtN7LNC6Mvu3Q3cktYjK1/W/TlmbDXXYN6rXvV3adFjznfNmQeu1cAQ12TGdBmkfh2qave7j9nbTtkQp3bhDmX6n296Q/UefbczoaYtsA9kKZeWlpbtHiEjXp+smbePV43ovArC889co2T+MmRGM42UlBR7JNMLl4H9LVu22PcqatKkid0vrcztVB6Yt1MtBj2qB3pRVAvkZvLbL+nqJm3V7qKW7pLiY8KECRo4cKBat27tLgGAc6dfv35asGCB2ytZvkneqde+WqTptz7oLomc9PR0vfbaa27PucWeKZe94IILgvYN8931tttuc3uRZa6XnLLwPPWemDU5j2O73hz3hN4/zwmj2VYBZ+HYiUzdMvt+vTpssrsk8op0JLNr165q27atHRpN++Uvf6lWrVqF7Pfp08ce+QQAAAAiwQTG4cOH+9qIESN0zz33hOybVlgBEyitijRktmjRQh07dsxX80Y9AQAAAADFX5GGTARnritNSHyJUlkAAIAypumAKdb3wMBSWaOpfjslUQmUyqIEImQCAAAAACKGkAkAAAAAiBhCJgAAAAAgYgiZAAAAAICIIWQCAAAAACKGkAkAAAAAiBhCJgAAAAAgYgiZAAAAAICIIWQCAACgzDhx4oRWrlyZr7Z+/Xp3bwDhKJeWlnbGfWwb8fpkzbx9vGpEV3OXRM7HH3+slJQUtxeebt26qW7dum4PQFk3+e2XdHWTtmp3UUt3SfExYcIEDRw4UK1bt3aXAMC5069fPy1YsMDtFReH9PkLk7Sy7TiN7lzHXZbTN8k79dpXizT91gfdJZGzZ88eTZs2ze2Fp379+hozZozbA0q2Yycydcvs+/XqsMnuksgr0pHMrVu35vjLUF7tyJEj7t7FTYZWJ4zVsMGDnXbPK1rnrgEAACgOTp8+7T4619KscHmH+g1L1J7oGtK+t/VAv2Ga/mmqux5AaVI6ymVTF+opL+yZdudTWrzbXVcIUhdOsZ5nhF5MivAvxozVmjPW73X42p16+v1CfEEAAKDU6dSpk6ZPn15MgmZ1XTPqZS14tqOSl6/X5yuq6M4FCbmOZhaWSpUqqWLFiurYsaPd2rZtq4YNG4bsx8fH6/jx4+7eIWyfp0fNd7ZH5utbd5GUok9n3G19jxupWZ8RplG2FGm57OzZs+0yMlNyYGzcuNH+EFer5jxXYP/tt9/WTTfdpCZNmtj9YDJWJ+gvLyTpYI2uGvX8ELV1lz35YT39+aFeauBsFjkmCE54QZ+dynq+wpOqRVPGav7WGuoy+nkNLtwnA0oEymUBIDwmXJqQmZmZqUsvvdRdWviio6PVt29ft+cxI5ljNX1daw24Ol17q9TXvnlfqN49TwcNmoVdLjt37lxf+aupmlu3bp06d+4ctL9371698cYbuZfLmpD5xELtaXiDHpnUX43thSZkPqZXVpVThzsmasS1RR+ogWBKXbnsmTNn7IBpQqNpMTExuuiii0L2o6Ki7H1CS1XSB1bAlBXChmYFvuj2wzRpZF19GGxU0C1rdUYjs5aPeOp9ZY0VBpTC2u0eJVo7ZmxZr02pUWpx1flaHLDOY0Lu/X77jnnFXemNVPpKa02IzLm/J2P1O1q2VYpq2VPXEzABAEA+nH/++Ro9erQuu+wyd8m55I5kJgxW/YzDUr2b9PQ5Gsk0Tp48qV27dtnNzBdigrh//9SpU+6WEZaSpJl3Z31HzBr59EY9H9F8byg0cHTU61ttgm8jbz9r+ciZ8g2Y5uN5UpJm6B5rm3tnfmZ9p7aXZB3TbVnPt11vjsta7jS/c86xb87n8R3LO0f3vHOs9z1XkPfEbVnnnNP2eeN825nXv8Y9vm+Z25znC37e3jn5b2/ahPmrc7yP/sJ6LaVckYZM84E2o5XLly+3m/lLUWA/X1JXaIMVwlTjcsUHhrDo9ho6NVEJs0bJ/sORGelMtPrPD1EDK2A+MG+rtWi0EqxlM0Z1UfTmNzTFFzSPK3m/9V97VEsNmDxV/ZvbC23H9++3/mPO1Jale9R2snf8w0qa7ZToeiOrp91jPz2guQ4vm12ActesAH1lz0IYkQUAAKWeCZqmKsxUWRRVyzmK6a+WFTannbNw6TGDGKYE1jQz22xgv1CYUPXYh4obY31/tL4j/nVYB1Xd9a5eCZ5SNPO5hdrjdo2UPcnyvinvXrfGCY0pm6zvwun2Mh3Zr2Szgf08CVpT4wY9Yr77PtpH9a3neSGXQJbFhC1v9HWqfZ7j+tTX7ncf8wtMFjNia4797DC1q7pLixJMiHX2/ajeGHu/7OvyyxzrOb3v/wa4o8XpHe/QM+77d2bly3o+yPtnAuaUhXvU4IaJzmtos0ZvpfTR8+5+Va1tvHWP968a8rzTu4wMsc9F9vOEJ8hrKQOKNGSaX3SmHLZZs2Z2MzXxDRo0yNbPj4ydyWF8WAKl6qv19vCguv/KSabR7W9UVytIZn63Xv/1z4JRcYoLmu6i1OLm29TTrItuoTatrV+UmfuUnJqhLes32sEwvq1z7DpXxquZFUq/X/+130hpGHIL0AAAACiwCy64wPf903wXNd9B/fvly5d3t8wnK8xN8o143WeFNTcAGjFddPfMServ1NIqpn6szAViR/bvCfg+a4WSN97UGr9djbTkfUq39mjevrkVTtdpjZWtUjZt0DflOqpnF+dSNMNeZu3boG07p2y3aTu1sVYf2Wqq8exNQvNCa8Mu6umW9zbt2sMKXX7BNohqcbGqrhh1HjnTCmC+F6hY8wLT9mtPPi9JTUl6Qwv83zvL9jXrrNBdTc3iW6q21Y9p1UaXBj2v7Vq7zkp01Trq19c559J0wJSs88ohcucdTLDXUhYUacg877zz7Osta9eubbcKFSqoevXq2fr5Ed0o1v6PLF8ydio5r2TqbhNVL1bh/50tU8n7vnVGQHVYSdPdXzBj52mbs0E+ZGj1O0ut/aww2/NXhXzdJwAAQNlSaOWy3gif3Z7VkA5m/CtLthJOcw2nu9zf0ZUmlJRTh95dlBUdPdXV5OqrrXC1SxvWrNbmDVuVXj1OsVXMujQdsFKRE0at8PXuY+5zPRFkFG2XFj3mnMeDCavs7W1pyUoOJw95Yfq+BCsMN9Q1va91vpNnK2cN9rx+52Xv6y70l75Sc99cpXIde+ta3xuQor32MO0RrXrZvaQt1P4pe5wR3fwI47yDy3ofTctRvhv0tZQNJbtctpL1oTIp8PBarQ9yTWNQ0Y0Um0cy9a67vDj+shxlqpXi4qwPUab2Jwf+aSNKsfUaKzbOnJCZqMf7BeO0WfmZhCj1E31oZq6NukRtLqNQFgAAIJJ+/vlnHTp0yG6HDx/O0S8M5jq9GX4lnHYZq7suyy59usiEkgEa2N5Oji43ZFWzvvs2aqU2zatqd9ICLdmabo9Ytoqtp6pWANtvbVPdfpxV2ulrM+52LiGzNVTvic5yrxTUVj1WsdlzcXC+MP2oetW3gtb0mfpsm1vim22du70f33nZZanuQj+7P1mkNeU6qt+g9sp6B2J0oT28WM1XxutrvomWXN5IZLi80uQ8zjs47310/qBwZOU8zfWbSTj4aykbSnS5rLnu8oZu5oLJw0qa43efytSFmpZtIh9/dXRFvKmN3awlHzl7eBPs1OjUUz0buCWvIQJedIt4tbI+oIfXrnOezw2EzuQ80WoR39oKoYet0Btu6s0pdcV6e/TTOR9nGQAAACLD3MLE3JrENDPzbuXKlbP1C1wumw9O+WcQ1UwocUcGfdKUvM8btotRyzbNVfXIHu1Nb6g27Rr7Sm/ttSHLSMMQ4wRY7UrSYjcsbV/2gdakW+Gux3XZw1xetq/RhrBHBP1ZzzVgkF8gdjRt19YK5Ue0bf3mPC6Xa6rL21op8chWfb3ZeQ0m4P813Bl3CnzewQR/LWVBiS6XNer0GWdP3FP78DK94A1zj/9arW4LPXJYp889uqtLHR1eNt3efqQ7Uc+0IZdqdcIEvZh0Sl2GPxQ84JkJhR4eoGbe842dpx9aDtI4d6TSzGz7oD3Zj3NspwXc59J3rub2JPYCJU13t8lYrXeX2hdj+q7rBAAAQGSYQQ0zWrly5Uq7mduVmDLZUP1t27blfZ/MMMR0GaR+Har6ykWnbIhTuxwjZg3Ve7T/iGOA6nGqb63zhcqGbWVlTB/7+k5z7ee9zmQ/WdeH5j4TaxZzfeK96lU/qyx1ysL0nLdg8R3blJa659ysiwb+1pnMyF73xAbFtg97SNCnwQ2jg9/upekAjXIn+/G/i0O2CYlcTQeM1pAOZ3yv4cEP6+m3oa7JtN6vgp+3Vy7rXH8beO4hX0sZUOT3yTQfUm/EMj093X7s/bUosG/uYzR06FD7dialmbmdygPzdqrFoEf1QC+GLoHcTOY+mQBQ6hXmfTIzMjL07rvvuj1npllzSZeZDChY3zD3/rzhhhvcHlCyFcV9Mos0ZJrQaC6szo8LL7ww/2W0JQwhEwgfIRMASr/CDJlAWVcUIbNIy2Xr169vj0rmp5X2gAkAAAAApUmRhkwEZ64rTUh8iVFMAAAAACUeIRMAAAAAEDGETAAAAABAxBAyAQAAAAARQ8gEAAAAAEQMIRMAAAAAEDGETAAAABSRQ/r8hTGa/mmq2wdQGhEyAQAAUMjSrHB5h/oNS9Se6BrSvrf1QL9hhE2glCJkAgAAoJBV1zWjXtaCZzsqefl6fb6iiu5ckKDRneu46wGUJuXS0tLOuI9tI16frJm3j1eN6GruEgAoPia//ZKubtJW7S5q6S4pPiZMmKCBAweqdevW7hIAOPe2bdumtWvXur3CFx0drb59+7o9jxnJHKvp61prwNXp2lulvvbN+0L17nk6aND8JnmnXvtqkabf+qC7JHKOHz+uTz/91O2Fp1KlSurcubPbA0q2Yycydcvs+/XqsMnuksgr0pD59ttva+/evW4vPDfeeKPq16/v9gCUdYRMAAjf5s2b9eSTT+pXv/qVKlas6C4tXMFDpsdckzlJK9uOy3UUszBD5p49ezRt2jS3Fx7zXXTMmDFuDyjZSl3InDVrlnbs2OH2wjN8+HA1bdrU7RUnGVqdMEEvJrnXEtToqlHPD1FbpwegkBAyASA8ZgRz0qRJ9nepTp06uUtLhhIXMrfP06NPLNQet+uopg53TNSIaykJRvFSFCGzdFyTmbpQTw0erGFeu/MpLd7trisEqQunWM8zIitgRlLGas0Z6/daBt+pp98vxBcDAABKJVMia0YwS1rALGym9NW07t27261Lly5q3rx5yL4pkzUltmFpeIMeSUxUgt1mEDBRZhXpSObs2bPtv/B75a8bN25Uw4YNVa2a81yBfVNee9NNN6lJkyZ2P5iM1Qn6ywtJOug3kmiWPflhPf35oV5q4GwWOSYETnhBn50qjJHLVC2aMlbzd7bUgEcfUs8Gbn9rDXUZ/bwGM0wKMJIZIY++/aIOHj3s9gDk5omb7lLtKjXcXskxZ84cxcTE5FK6WnwV9kjm3LlzfSOTR44c0bp163zXXAb2zaVeb7zxRngjmSZkTuqvxvbCFH064zG9knydBrdZo8SF7jinvU0X7TbrVpXzG+10t19VQ71H/Vr75yRoTbqzS5aG6j1xkvr/HGzk1FKto4ZOvFvmcNvnjdMU7znzGFVNSZqhSQmr5P901TreoUfvvla1rceB6xvcMFGP97deZUqSZj5mnWcN73V7r8HvdXnbeDt771Hge+b2073n9e8P/Fn/yu/zeO+V+ccIta5qLvtks11vjntC7+d8w/N+/hD/Vt77+2O2f6fs73thKZXlsj169PCFxuXLl6tZs2aqXdt5GwP7ZnvzF6TQ5bK5hDAvDAYONrphtMHCKXpg3lZ3oRTVcpDG+UJpQCmszXmO/qdNqF2hmN7X6OdFH2mb3zrv+X3B1+laTzla04ZYK3ME1IDzv9Rdf9QLmd55nCJkAi5CZmT8z6x79cofJ6tqVLS7BEAwg18er6d/M1r1qgf/cl6cETKDMyHzH//4h37zm9/Y/VOnTmnXrl265JJLfP39+/erW7dudv+sQ+YqK3W4y392A4UJaSNjFtrBrZwXKvwD2z0xWuQ9to/nhZzswcUXyLx9yzkhs97ScZp5oJcbVtx907MCaCAnkKY7gane0mzH/tkNmNXdYJlt2xYbs845WPgLXJ8tSLbQRi9U53hN3roQxwn1PO7rv7ZOwPvlhUnf/paA9yzHPtmCZuB7mM/nN8cKDNH2oqz/Hsx764V5338T9nNHXqkrlz158qQ9WmnCpGnmL0WB/XxJXaENJifWuFzxgQEsur2GTk1UwqxRzofJhEtTuuAXME34M+UMM0Z1UfTmNzTlqfflFKYeV/J+K2BGWWFv8lT1b24vtB23fukcVKa2LN2jtpO94x9W0mynRNcLmKfdYz89oLkOL5sdXslrdAu1aW2dbOZmzXviKc37x/N20I1q2VPXEzABRNDRE8dUv1as/QdFGo0WumVkZqhqxcruJwelRbly5Xxls2ZCpMB+ZFlBY5gTbJq2aytTz7d73Rqld+mla6zOka3rtcn62pmyaYO+sfJog7btnBB0FpoOmKLnfCGlumLrVbWeaL+Sg37VTtFee0V11a0fmEBTtNn6sp1uvYY27Zyzcl7DEW1bv9k3oBJKjtfUtJ3a+F5zjFq2aa6q2qUNa761t/dJ2WR9xzfhvIt6BkvFAXzP06W3871fTXVdjw7Bj+0qyD6hFOxY27V23R4zdKlfX+e8tzEB/02UZEUaMsuXL2+PYsbHx9utSpUq9iilfz8/MnYm5/kfd06p+mq9lUytANn9V05yi25/o7paQTLzu/X6r38WjIpTXNB62yi1uPk29TTrfMFwn5JTM7Rl/UbrnGpYodc5dp0r49XMCqXfr//aDbC5iVb7YVPtYGqC5uKPnPO88bZCKPsFAAAooypUqGBfomWaGe2NiorK1jffWQtfU13e1k4U+nrzthxh7qyYUbq7vfk97pM9mhpSmpL3WeurxSk2RyGju84KS4sec4/3RJAy3V3valKQ50pL3meX2O5+9zH3XMzonrPOiOkyUo8M66A0s9497pGVL+v++wJGHT15PE9+FGSfUAp0rJQ9IUJ/6VCkIdP8lch8iCtXrmy38847z/5rkX8/P6IbxeZ/GDljp5LzSqbuNlH1YpX33048mdaH8FtnBFSHlTTd/SCOneeW1IbDlM8O1gPzdqrFoMn2CGttM6o5/h4lrnM3AQAAwFn56aef7Nl3Tdu9e7c9sY9/35TMFqZqcbGqbv30RgVXzXtFS+yRu7Y6+4y5XW9Od0s3TVVf4rMa0qGquy4IN+xUax6vVjm++LqjoPb1heZYWS1rpNRiyoHt5dmfq3psPZmeKQf13zdhhlO2a8pFH0zYpuZ3TFXCo33sUV5zTeIzzw5Tu8NWoBw5M/ulb3k8T34UZJ9QCnSsmPpBQn3pUbLLZSvFKdZ8GA6v1fpwQ1h0I8XmkUwztpgh6ihdHH9ZjhHESnFx1gcqU/uTA8ewo6wPYWPFxpkTMtdY+n2QrDYrnEmI3PLfqJY365ZeDRTdfpgeNKOaVmhdv46UCQAAUPLs0qKE+TJFk9vXrLNH66rF1XcCWtOu+rUJS0f2aG96NXXocd1Zl8rm4JWehrB92QdaYz13s/iWQQZvcilpDUNMqza61Hp5pjw4x94pSVr8qSkXba7LWgak25gu6tnZG+XNu27U9zxJi9xQul2ffLBK6X6lqIEKsk8oBTuWN5K9Uh9+4rw7KUnv63PrLXHKbk9p2XNm0GqYZn0mnVr6nD2A9ccX7Y5eMINZw17U5/aexU+Rhszzzz/fLkMwk/uYZureGzRokK2fL9HtdUM3J4QlzXlFvhiWulDTfNdXBqqjK+KdctQlHzl7ZKx+R8uscFejU097sh275DXqErW5LGcsjG7h/JXn8Np1zvOlfqIPfddNRqtFfGvrA3p2oTBzX7Kcj1OGdtrDrlGKs9M0AAAAztYFF1zg+/5pvoua76D+/ciWyzZUu7pr7DJPM8mLGam7xzerjBfiLMHCVoE01W+H9VF9K7zYt8W7b74ymrnPESBrBtojWvXyWKcKz79s9ZH5Su8yUiP71PcreTVtpBV88g5/Jizefa91Lr4yV6fdO/MzfZPjOsbsfKO8H3ySM6AG8p7He82mLNc3SY+7TaCC7BNKAY/VdMBoe0TWe28f9JtgqaQr4bPLOgJnczXXMTqzs1qPg95yJOfssc4MsJcGmc01yAy25r6cfmWw2WemNauzz1xrQmKLQY/qgc7JwWe8tTnb3FV3SfbX4u3bK89xUKBMmMzsshHx6+l/0vIJ/9R55Yr0b41AifOrvw7Tq0OnqEpUyZv8h9llgzt06JCmTZuma6+91u6fOHHCnk22UaNGQfuZmZn673//q/Hjx9v98HkzkLqzp4bKDUFmHS0qTsg8L/RsqucFuS4SJV6pu4WJuU+mqXn3RizT09Ptx95fiwL7ZorpoUOH5nqfzNLACaXmOkzCJJAXQmZkEDKB8BAyz43CDJnmu+inn37q9qQzZ87o9OnTvu+fgX3DfD/t7N43M3zhhczA21gUJUJm2VTqbmFy44036qabbrJHJ03r16+fevfuHbJvAuaFF17o7g0AAACcHRMYTWWd13r27Kk+ffqE7JuW/4AZLvc2FpGaVRYoJop0JBPBMZIJhI+RzMjIbSRz5syZsv7f4PbCc9ddd6lGjRpuDyg9GMk8NwpzJBMo60rdSCaCq9NnnBISXyJgAigWzLVI5pql/LTI37y8pFij6VNuVKunZmtFhtX97//qVw/fqDs/SnFWAwBQBhEyAQBFww1grbzmBbMSrZ1G39hXF6a9r6GTrNf0+nvaW72XhnWKcdcDAFD2EDIBANmY65XuvvtueyZF08wMjA8++GDIvimTNRNp5GbX0om60gSwi/6gT558R5us9sEV+/XMe1/pqLtNifWLP+kj9zXZ7aHhujLaXQcAQBlEyAQAZGMCY1xcnGrVqmU3Ezpr1qwZsm+m+zfLQluj+V+uVbou02MDblJdd2nDbo9p/sArVGXve7p74o1qNfttHbDXuCWoD4/Xm979nLxtvFFQ37bS6vlDrWV/1DPr3LjqjZj6ttmlf780MGtfv+Pa4df0/+M/ypq1PsexvfNwR2Gd/f3LY4OcOwAAZQwhE0Cpc3xdgsY8ttCKFiiIn3/+2Z7ef+nSpXY7deqUkpKSQvbNVP+5+u8qLUy3fl50hboU5AZwJti99L9aGueOgt7aVxf+8HcNnhvOKKgJmPdpcZOZzijjyD+p2wVfa+K8rJAqWf13d+rO+9xjm3629R4rQL5incdPbjcH81x/1d/MawUAoAwjZAIoNUy4vLvfrXp6awXFWvHjkyf66VYrbO5z1yM85cqVU8eOHfXLX/7SbmZSn3bt2oXsn3de7v8r2XVgj84md+3aslIrrWB37aVXOaOgv+igPlWlnd+t1sY8r+lsqP+5c65e+pV7jeSFF6qJmaMoba++89v32uvv1W9NAHaPrR++UlLASOTq+TNyDZC7lr6sp77PvWwYAICygJAJoNSo1HaYZi54WTdlrNBXG5boRN8Fen1iH9Vz1xemH3/80Z6VNa/AVRKYkGnKXytXrmw3M1JZtWrVkH2zfW4a1q0vk9sK6sChH+yQ+tnHf3DLWf8SJOwla87cW5z15tpPd6kt24RDwfYNw64EPbj6oK7tOEDdLnCX+Tvygf6atFa12g7QLWfzYgEAKAUImQBKDWck8w69HX2lrmjTXRXfK5qRTBMwJ06cqE6dOqlly+J3/878ini5bK0L1cIEsyCjg+GoW+siO6Ree/3fsybXyTHBTqyGDvyns9wueXWZUts3/Scc+ov+GE4IrN5AF0W5j02A/c9H9jGe+GXwe4F+tnKellbqpb/0bSXm/AEAlHWETAClhjOS+boeaH7SigVVdN2joUcyJ0yYoH79+kWk3XHHHbr88ss1dOhQ9+glW6TLZXVhXw29zNSiBlzr+N//1ZAwrqts2KKjOloh9bNv/hPkOsl88q4PDfDZx885E/V466tfqEuypcXskxblZIXcnr9nVlkAACyETACljgmb06xw2dDtB/P4449rwYIFEWulJWAakS6XNdr3n6MPfn25qv7wd13nla6+d1rD+16hKu428q3zSlqtUPrsH/XMges087fOZD++fa3WK5yJf6yA+2AXv+d9faeuaJ5z9qFrm1fXS8+a9c59Lufc7h8ozSjpw841myFce/0U3d/W90oAFGMZGRl644038tXeffddd28A4SiXlpZ2xn1sG/H6ZM28fbxqRFdzl0TOa6+9pp07d7q98Nx2221q1KiR2wNQ1k1++yVd3aSt2l1U8stSz6VfT/+Tlk/4p84rl/NvjZMnT7ZLZr0RypMnT6p8+fK+MBnYP3z4sB5++GH7diaRZG4f8vvV5a2AN73QApy5BUn/D9eq7fV/z5ocCPDzq78O06tDp6hKVGV3SckxZ84cxcTEqG/fvu6SkuOb5J167atFmn7rg+6SyNmzZ4+mTZvm9sJTv359jRkzxu0BJduxE5m6Zfb9enXYZHdJ5BXpSOaRI0d06NChfDXzZaZ4ytDqhLEaNniw0+55RevcNQBQkt111112Gz58uN1GjRqlESNGhOybgFmjRvBrFQGgNDhzJtuYTHbb5+lR7/tgjvaI5n/rbgeUIaWjXDZ1oZ7y/0Df+ZQW73bXFYLUhVOs5xmhF5NS3SWRlKpFU/xey+B7lEh6BVCETGA0o5L5aaVhVl0AZYO5HCA6OlqDBg2y20033WRfVx+qf8MNNygzM9PdO4imA/REYqISrDauT317UYMbJtr9hMRJ6t/YXgSUKUVaLjt79mx7kgiv/HXNmjW65JJLVLNmzaB9U17bp08fNWnSxO4Hk7E6QX95IUkHa3TVqOeHqK277MkP6+nPD/VSA2ezyMlYrTkTXtBnp7KeL3JMwByr+TtbasCjD6lnTfe5jrr9iL8YoOShXDYyciuXBZCFctlzo7DLZefOnesrfzWVduvWrVPnzp2D9vfu3WtflxlOuez2eeM0ZeEeO2Q+bqfLFH064zG9sqqGek90A6cZ+XxiofY0vEGPTOqvn919AlXreIcevftaBV4OnpI0Q5MSVmXdf9g9jnPovI7lnY+3d0PfeTnHTda1Q9to/Rzr/ALWG9mPX00d7pioEdfW8b2mdO95UpI087EErSnXUUMn3q1r62zXm+Oe0PvpXj/rdZSz92mhjXm8T+4pIAJKXbmsKTWoVq2a7y/f5q9I/n8xD+yba35yLU+wQlnSB1bAVA11GZoV+KLbD9OkkXX14Vj/EUG3uWWtzmhk1vIRT72vrMHPgFJYuzkjihlb1mtTapRaXHW+Fges85iQe7/fvmNecVeagGrOyVda641auvunrtCGrVLUJfH6hQmU0S3UprX1Kcz8Thu+LsShWQAAgDLkxIkTWr9+vd2++eYbHTt2LFvf3KqpUJjw9ZwX4PyZwDbVHv3867AOIe8t7B/MnjEjpY/2Uf1d72rSI/OVVZUb6lj+gdeMsj6qXvV3adH0mfrMV5xn9edsULxZb45t+gnOsU3AnHmgl/O89r5HtGreG3775oMVIF/wD8qBQr5PKCmKNGT+9NNP9mild281c2+5wH6+uKFMNS5XfOCQYnR7DZ1qfQhmjbL/WiIz0mk+FM8PUQMrYD4wb6u1aLT9AZwxqouiN7+hKb6geVzJ+61PTFRLDZg8Vf2b2wttx/fvt0JtprYs3aO2k73jH1bSbKdE1xtZPe0e++kBzXV42Ww9/X5BQmK0GsXmMp0hAAAA8s2U+HuDGmaAI7BfOKyQ98abWhMyWeUlRZutL77paqhrersjnE276tcdrBi5a53W5HXtZ8om63uz9eQN26qdPSzYVJe3rS8d2aqvN2clxQY3DHNGEpu2UxtT/eseu+mAKXrON7JaXbH1rOc9sl/JR+wF+bBdbybkFiDP9n1CcVCkIfOCCy6w763WrVs3u5my2MB+fmTsTLYCX36l6qv1Zriwpbr/ykmm0e1vVFcrSGZ+t17/9c+CUXGKC1qiGqUWN9/mlK/6Rhv3KTk1Q1vWb7RHVuPbOseuc2W8mlmh9Pv1X/uNlIZQKU6x9sCldx4Z2plcgDuXAwAAIKQKFSqoYcOGdjMlxVFRUdn6ppou0o6ufEMLVpVTh95d5Fy5mV9pSt53FskrLVnJZncz8ulW2wUrrQ3JjC7e7VXq3edXcps/+95J0Pt7Gqpz7+Ajtmf/PqE4KNEX40Q3is1Rp56njJ3KM7e520TVi5UZBA1PpvXB/9YZAdVhJU13P4Rj52mbs0HeottrwC1dVDtzs+aNN/sX1uRCAAAAZVfRl8vu0qeLTJnrAA1sX9BbMrmjhwVVPVaxZndzjaNd8uq1Gc51laFUi1Nste16c7p7jaWpFEx8VkPMCGp+HVmpxUnmmtVh6hPnLssmEu8TioOSXS7rjvzp8Fqt97smMlfRjZRXBap33eXF8ZflmDioUlycFWwztT85MPxFWR/8xoqNMydUQ11G+394EzUrzEmIzPWkTq27abN0VxfreFGXqM1l4ewNAACAvJyTctlqHdVvUM6JfMIXo5ZtmquqFcQ+X/SZU823fZk+XJVuHbqHuuY1M05MK7VpbgXDPEprd7+b4Nx2ZfsabTADndXjVD8wg3qltwVhhdwh3kxCwZz1+4TioEhDpilNaNWqlT3DrGnVq1dX69ats/XzJbq9buhmLpg8rKQ5fvepTF2oadkm8vFXR1fEm9rYzVrykbNHxup3tGyrFQ079VTPBm7Ja4hgF90iXq2sD9rhteuc50v9RB8mpSqqZU9d3zZaLeJbWx+Kw1boDTf15sI9tnNe7jIAAACclaIvl22o3qOdWVXPRkyXkRrZp76OrHzZmWTSf0ZXd5vQYtR55L3OZD+PuRV3po30n/hHatC+rtab9WZmVyvwDb3XzOzaVL8d1kf1j6x0JrG8b74ympnAm53vvO5LcK6ptLf3u1eo73ihROZ9wrlXpLcwmTVrlnr06OG7Jcny5cvVrFkz1a7tfCwC+2b77t27q2nTpnY/FN9tTNy+PWGPd8uPoLccMbPHTshWimomAZo25FJ3+Sl1Gf28Btsbu7cV2WpGJ91l5r6cfmWwUS0HaZzfSKWZudZMLJQlSi0GPaoHOic75xK0AtZsc7d+sfZZ67ncRRbnvJyzBsAtTCKFW5gA4SlptzBZtmyZ+0j6/PPPVbVqVcXHx7tLpK5du7qPirfCvIXJoUOH9Oyzz6pNmzZ2/+TJk/ay2NjYoH1Tibdr1y6NHz/e7pdW3sy11X23XzlbQW7fgmKhKG5hUuT3yUxOTrb/emSYD/H555/vu4l3YN/cp+hPf/pTrvfJLA2cULrTCaK9GLIEckPIjAxCJhCekhQyMzIydPvtt7u9nMyt4l599VW3V7wVZsg012Nu2LDB7YXHTF7pH9ZLI0Jm2VHq7pN52223adSoURo+fLjdzOO77rorZP/BBx9Uo0aN3L0BAAAQrs6dO9sN2VWsWFEdO3bMVyvtAROItCINmaZkw7uoOtxWGFNIAwAAlGbmGsPf//73djOPgbyY6z2fT0yM0CimYa4BnamEREYxyyLqpIqBOn3GWR/AlyiVBSLk+LoEjXlsoXa5fQAoa0z1mJnjwrQbb7zRXQoARYOQCaDUMOHy7n636umtFRSro/rkiX661Qqb+9z1AFAWmPLO6667zu3JftyiRQu3BwCFj5AJoNSo1HaYZi54WTdlrNBXG5boRN8Fen1iH9Vz1wNAaWeuNzShsnLlrImK4uLi1KVLF7cHAIWPkAmg1HBGMu/Q29FX6oo23VXxPUYyAZQtZubUZ555Rr/5zW+ytZdeesndAgAKX5HewgQAzlY4tzAxYXP827EaPbGPGrrLAk2YMEEbN250e5FnbhXw8MMPq2XL4nmrlcK8hcnMmTNl/b/F7YXHzCxeo0YNtwcUHyXtPpkvvvii+0j65ptv7El/GjbM+k1oPmslQWHewgQo60rdfTIB4GyVlPtkLl++3L43cHENmoUZMh955BEdP37c7YVn0qRJqlSpktsrS9bp1Xun65PzO+uux/6g9tsTNWb6UtX97bN6qG+Muw3OpZIWMv3NmTNHMTEx6tu3r7uk5CBkAoWn1N0nEwDKik6dOtn3+zXhCRGyzgpggwdrmNfG/l2rjzqrSq62un1IN9VI/VQv3mW9JitgHq7TWb++joAJACi5CJkAUEjatGmj888/3+2VLSZcT5061W7du3fXU089FbIfzgjm7vf/qhEmgDX/rf6amKgEcy+3X6Xq33NXqeTnzMGa5r4mu039g9pXcdcBAFACETIBAMXcOi39YJMy1Vz9/thX3hhfg14PatIfOqjK7vf1zJ2DNWzKe0qx15gSVDPaOUULnQUmpTrbeKOgvm3NAOm91rKxmrPKjaveiKlvm91a/Nc7s/b1O64dfk3/E/9R1qz1OY7tnYc7CuvsP1hPvec7m5znDgBACUPIBABE1M8//6wPPvhA7733nt1OnjyZo58v69Zr3Y/Wz+ZtdEVBqkhNsHviDW1u5I6Cju6mGlvf1NN/D2cU1ATMJ7Su9SRnlHHyILWM2qoFf8sKqZLVn7NH1z/rHtv0s633WAHyWes8Mt1uDua5ZusT81oBFJqMjAy98cYb+WrvvvuuuzeAcBRpyJw1a5bGjh2br7Z9+3Z3bwBASXDeeeepR48e9mQjplWoUCFHPz9279uvkLksDLu/3qDvrAM0a3OlMwraNl5ta0oHN63X1jxTZgP1fPClrEl4GtRTrKnuPZisH/z2bfbbP6qP2cQ9trZu0FcBKXNd4iu5Bsjd77+udzadzSsFEI7Dhw9r5cqV+Wpmpt4ya/s8PTp4sO6d+ZkO2t1xGjb4Ec3/1lkNBMNIZoFlaHXCWLc0ymr3vKJ17hoAQOQ0qBenKPdxQaQe2GeH1G1v3uf+zp4eJOyl6rMZdznrzbWf7lJbtgmHgu0bhh2v69WlP6rZr3qrZbAX8+NS/eutTYru3FudTEgFUKycOZPtZgwhOQHM+32RFcxKtKYDNLhPfR1Z+bLut17TlIV7VK1jD3Vt7K4HgigdITN1oZ7y+0APu/MpLd7trisEqQunWM8zQi8mpbpLIi1Vi6Y4r2XMK9mja8bqBPsD7r3WwPUAcK5FvFy2Tl3VM8EsyOhgOOrUrWeH1Ga/fTZrcp0cE+zU0bUjX3SW2yWvLlNqO9t/wqHRui6cEFgnVnG++YysALvoP/Yx/tA1+O3Btn20SJurdNaggc1V0V0GoHCYycaqVq2qESNG2G3IkCG65pprQvZvu+02ZWbmVWWQok9n3G0HsAY3THR/zzyr35x5X3M/K6zvi0Wn6YAp7mty2nN3X6va7jogmCIPmebD6s0o2L9/f40bNy5kv0mTJu5eodmha+w8bavRVaPc//Bn/KmuPn/tfRVKzsxYrXeXbpX8ns9uzw9RW3eTs2IH5rGabz1FIPNa//JCkk53HW0/59MDmuvwsukETQDFSqTLZdWgl359lV2Dmv1ax3WJeiKM6yobXNZGl1gpc9uGFUGuk8wn7/rQANve/JszUY+3vnasLso2Q2z2SYtyskLu7wYyqyxQBMx9fKtVq2Z/zzStUaNGql27dsh+bGxs3rNgb1+mD1elSw1v0JD+3hBfjDqPnKIR19ZRStIM3TN4sCZ4NaZuCeqwR+bLqzr1tvEGEnzbarveHGctGzlTXl71Rkx926QkaebdWftmHdcJv6af5D/K6luf89jeeTijsO7+/uWxQc4dCFTCRzJTlfRBkvUBqKEuQ7NCXnT7YZo0sq4+HOt+kPybW9bqjEZmLR/xlH8oDSiFtds9SrR2zNiyXptSo9TiqvO1OGCdJ+RooxVQ55hz8pXWeiOWWfunrlhvB+bBVoDMLkNb1m+0X2t8W+eV1rkyXs2sn4fXrqNUF0Cp1nbwc3p8UCtFbX1TD3q/X/9xSr0HdpAvl/nWeSWtVii9b6zm7L9W9w93Jvvx7Wu1+8OZ+McKuL+72e95p+9R4/Y5hzKbWenw4/vMeuc+l3eN8g+UZpR0lHPNZgjNfvuQhnYgYQJFxQTN5cuX2+3rr7/W0aNHs/VPnTrlbhme7WvWaY/1s0HbdipIFakJdpMSVqm6Owo6rk997X53umaFMwpqAuZjHypujDPw8ddhHVR117t6xf+iSaufuKGdHnGPbfrZ1nusAPmCdR5WXA7OPNdzC+3XCuSmSEPmiRMn7A+vVzJ18ODBHP18SV2hDWbEr8blVvByFvlEt9fQqdaHbdYoXVvH6nsjj88PUQMrYD4wb6u1yBkRnDGqi6I3v6EpvqB5XMn7rQ91VEsNmDxV/f3y3vH9+62gl6ktS/eo7WTv+IeVNNsp0Q0+2jhbT78f3rhqnT7j7HNs7fazeOdUT7Hm9RiV4rIeA0Ax8sgjj/gmcFuyZIkeeuihkH3zZS8c5pYls8zvca955a5WELz/Jb/lbhvVzS8MBt6L0mrPmNuf2Kues/pTs0Ket+04Jyhmf95xunuUtX3gvSwb/y7r+H7rchzbO1d3G+/YvomF1Fa3P+c8T26hFMDZMRUVzZo1s9sll1ySo58/KdqbfMR9XBAp2mx9oU1XQ7Vp50TUpu3aqr6OaNv6zXlf0xnTRXfPnCRvADWmfqxMYf6R/Xv89m2o3sP62wHYOba0e92agJHI7XozIbcAmaJP33hTa0ImUCBLkYbMihUrqlOnTr6SKVOKENjPj4ydyXl/8HJI1VfrrWRqBcjuv3KSaXT7G9XVCpKZ363Xf/2zYFSc4hq4j7OJUoubb1NPsy66hdq0tpJe5j4lp4YabczU9+u/LpzyXQAoZiZNmuS77CHclmcpGgBEUPny5e3vnaZVqVLF/o7q3zfrwxejC2ODX28dnjQl7zPJbZcWPeZWWzwRJOwdWelUxFnrzbWf/rJNOBRs3zDseydB7+9pqM69O6iqu8zf0ZVvaMGqcurQu4sdUoHclOhy2ehGsfm/6Dhjp5LzSqbuNlH1YhX+QGGm9QviW2e0UYeVNN39oJvrRZ0NAJQB5v5rKSkpdktNTbVnJPT6ppn1AIBzK9LlstVj69nBLOfoYDiqK7ae2buhek90KyLclm2CnWodnSo9a7ld8uoypbYz/CccerRPWCGwWlys9cwuK8AuTjLHGKY+ce6ybHbp00WrVK7jAA3MVsYBBFeyy2W9ctHDa7U+3IsSoxspNo9k6l13eXH8ZQocyKwUF2d92DO1PzmwRj7K+gXRWLFx5oRqqMvo7L8kZj3UK8ex8qeSc2x7xNRddHy//Th/YRhAYZo3b57+/Oc/223MmDE6duyYr2/asmXL3C1R2HKUqhaCnOWuAEqCyJbLmorVXrrGJLuAax23z5sSxnWVMWrZprkVUndpw5r8R9RA3vWh2e3SogRnoh5vfbW4+tkHa7JNWhSEFXL7DWJWWYSnRJfLmusub+hmLpg8rKQ5fvepTF2oadkm8vFXR1fEm9rYzVrykbNHxup3tMxMGNupp3o2cEteoy5Rm8tyxsLoFvFqZSU632Q7qZ/ow6RURbXsqevbRqtFfGvrw3fYCr2Rnoon57HtSYKscBssDAMoHszvNgBA8RLZclmjqX475VkN6VBVu999zFe6OvPAtRpoTw7i8K3zSlqtUDpp5ExtaT1SI+3JfrL2HTZ4ZFgT/8R0GaR+fs87ZUOc2uUYymyodnXXaJJZb9/n8g7d4x8ozSjpvc41m8E1VO/RdzvznABhKJeWlpbt7rIjXp+smbePV43os6ktD27WrFn2NPZmOmjDjGKavxh54TKwb7bv3r27mjZtavdD8Sbb8Y2Dmgl7Hn3IuWbSzOg64QV9dqqrRvluM2Jmj52Q7T6XZhKgaUMudZefUpfRz2uwvbGZAdbcUsSMTrrLzG1G/Mpgo1oO0ji/kUozc62ZWChLlFoMelQPdE52ziXo7wtnm2E/vxqwr+Hu36tBwLGzlgNlxeS3X9LVTdqq3UUt3SU5HV+XoPFvx2r0xD7W/xaL1pw5c+zKDOPyyy/Xo48+qieeeEJr1661lw0dOrRYBM9fT/+Tlk/4p84rV6KvmgAK3a/+OkyvDp2iKlGV3SUlh/l9FBMTUyL/2PVN8k699tUiTb/1QXdJ5Bw6dEh//etfdfHFF9t9c29fUy5rbmsSrG/u7Zuenq7x48fb/cgxtw95Qu+nWwFvYmEFOHMLksf0yqoa6j0xa3IglG3HTmTqltn369Vhk90lkVfkIXPHjh1uLzzDhw/PM2SWdE5w3ElgBMKQW8g04fL+Jz5WzICeitpygS48b54W/zxMz1phs567TWHzQmbDhg01atQo+49qJmC+8MILsn7fEjKBEoaQeW4UZsg011vu3LnT7YXHjGya+2dGFiET50ZRhMwi/XYxYsSIoLMK5tZKe8AEEDmV2g7TzAUv66aMFfpqwxKd6LtArxdhwPR33XXX+ao2zIim6QMAzj0TGM3v5/y0yAdMoHTjT9gASg0zknl3vzv0dvSVuqJNd1V8r59ufWyh9rnri0qbNm3UpUsXt+cwIdMrzQIAwLmOM1EJMwrzWscYdR45UwmJjGKiaBVpuSwAnK1IXZM5YcIEbdy40e2dnejoaD388MNq2bKlXZ72xRdfqH79nBPI79mzRzfffDPlskAJQrnsuVGY5bJAWVfqrskEgLMVTsgsambSstmzZ9tB01x3vnDhQnu5uUemuTVTnTpZf6Lu06cPIRMoQQiZ5wYhE/+/vXuBj6q893//5abBIESIJmgULAgJFBKJeKnSGLTIRaVWSzmKBmgPlvgXiqmKULBaQ1GLbEDDi57uQNjYg2z3PsXKtSpm0xaVIgSrXJQtFBCiAw3ISKhcznrWrDWZmWRygZUxl8/79XqaPOs+E0Pnm9+znoX60+TuyQSApsg8islMUvbMM8/YH+ZM4DTN3Ffetm3bYN+0xvhhDwAAoC4ImQDgAXMfZqtWrZweAABA80XIBAAAAAB4hpAJAAAAAPAMIRMAAAAA4BlCJgAAAADAM4RMAAAAAIBnCJkAAABoNr788suwR0vVpi1ZssTZG0BtxDRkFhQUKC8vr07tk08+cfYGAAAAzs3Ro0ftz5d1aZ9//rmzN4DaoJJ51vzaVJinsTk5gTZxkbY4awAAANB0nDlzxvmuel8Uz9NE97Oh06a/+r/OWqD5iGnIbNGihS688EJ17NjRbu3atVNCQkLUfuvWre19auRboZmhv9APztTqfc66euBbMcM6T65eKvY5S7zm08oZgdfyyKLK0TVwfms9wRZo0OLj4+X3+51eLOzWH6b8SHffPVH/8dHXzjIA9avh/t5dcMEFMf43qHFo27at/Xk0NzfXbqNHj9ZNN90UtT9q1CiVl5c7e0fzhf5n3v/R44V/U4c7nlRhUZHdpgy7TPv++JR+9uJ6HXK2BJqDmIZM81eg+++/X1OnTrXb4MGD7V/eaP0uXbrU+Jcj/6ZCPZq3TDsTsjXB+YWeN+4S/XnJKtVLzvRv0h/f2iGFnM9uc0Yrw9nknNiBOU+vWqeoLBA+H1tW5UoADdBll12m119/3enVo3cLNOru2fryez9Uz9bOMgD1qwH/3v3zn//UX/7yF/vfIIQ7fvy42rdvr27dutnNfN7s1KlT1H5SUpIdTKv1yTr96W9fSpffodH3fMtZKHUfMVZDrB/B0Y1rtO5/3UrnL/Tq28s0LVggsfpOsbNSJfQXr4o6KBqjmIdM85egr776ym6nT5/WiRMnwvp141PxmmIdUoKyxlSEvPjMsXrm4Uv0p7yQX1K3OdW/YDXQabkzQ0NpxFBYu01UkbWjf3uJPvLFKfU7rbQ6Yp3LDr4h+warkVZAXWiuKViBdCuWFfv73i2xA3POiJ6BBaF872rrDvNaR6iHswhAw/bUU09p7dq1evXVV/Xhhx960v71r385Rw9xXa6W/Ncc3X8lCROImTr83u3cubPK3+f6aFu3btWTTz6pQYMG2RU5VGaC5oYNG+z2wQcf6NixY2H9kydPOlvWzifvb9F+62tKRj9VREyjg5I6X2h9PaLP97sj4PZq5cKtSn+ySIXThuky0y8MD5MpbjX0mXsijgc0DjENmV9//bU++ugjvfPOO3Y7cuSI/Y9haL9O7NBlfU24WumRZcT4TI2ZZf1yFkzQgESr71Ye54xWihUwTTUwIXtSoPI5IUvx25ZqRjBoHlfpQesfgrg0jcifpXtC8t7xgwetUFuu7W/tV0a+e/wyFc8PDNE1AfOXc4t1yjn2c1ZYLFs3X8+tql1dNXHYFPsaezv9MInDNLlojnK+7fQBNHgXXXSRHTQ//vhjvfLKK540hr8Bjc+KFSuq/H2uj2b+qDVkyBDdfvvtztkRKS4uTunp6XZLS0vTeeedF9b33lEdLD3qfG9C5FjZBc/u/dTXFJv3btH7lCzRhMQ0ZJpf4H79+mngwIF2Mx++Ivt14d9Tehbj2316r8RKplaAHHRrIJnGZ96pbCtIln9aor+HZsG4ZCWnON+HiVPq90dpsFkXn6q+va0UW35ApT6/tpd8aFdW0zMCx068Ll09rFC6u+SD+hm+C6DBM/+2PfHEE3r66ac9aXX9txLAN2/SpElV/j7XVzMhE9GZOT/MPaummTlAzGfU0L5p3mqv5KT2zvdA09eoh8vGd0lSJ+f7WvPvUWlNydTZJq5zkkwRtHbKVXrgfwMVUJWpeLYzXNbcLxrYAAAAAA2A18NlOyR1lhkUu2/L+xH3UB6xPh9+aX3toEsuq+ZTZftkkUHRlDTu4bJtrV9I8/tatlklIfdEViu+i5JqSKbufZdd0/sospDZNjnZCrblOlgaObNsnJI6f0tJyfbYXGVNKqqYFMhqBZOHVDoWAAAAYq9Nmzbq0aOH3a688spK/bq6OGuIbrKHvRZr9Xr3M6KZcfbftGp/yPBYx74/FgYm+/nkfW01N3N2SFZ1GRRobBr1cFlz3+UdA80Nk2UqXhjyOA/fCr0QNpFPqERdm27Gxm7T2jcCe/g3vaZ1ZsLYGwZrcIoz5DXuSvXtUzkWxqemq5f1j0DZ5i2B8/ne1p+KfYpLG6xbMuKVmt7bCqFlVuitbeoFAABALJnhsGYGWdPMI/TOP//8sH7dh8t21w9n/Eajrzmjv/3OnTzy51r0txa65iez9HRowrSkZF6ikqesbX61Qvvb99eYnzHBD5qWFkeOHAl7Rkjuy/l68YGpSoj3vmY/f/58XX/99fbU0Mb7779v/7XIDZeR/SVLlmjYsGH29NHVcSfbCY6CNRP2TJscuGfSzOg6fa7Wn8zWhOBjRszssdPDnnNpJgF6YfRVzvKTypo0Rzn2xmYGWPNIEVOddJaZx4yEDIONSxupKSGVSjNzbfhjRuKUOnKaHvtuaeBaIougtsA2Y08vruIRJc7+/UvCzuuKPD/QlOUvX6Abu2Wo3xX1MTHD2TOT8YwfP16LFy92lsSYeZTCc2/quNMNSNGY52fp9m9V/rD0vdnjtGH679WyRUz/1gg0Orc+O1aLx8xQu7gLnCUh6vh7h9r7uHSPlry3UrPve9xZ4p3Dhw/r2WefVdeuXe2+uV3LDJc1jzWpqm9G4n355Zf24/XOlXlEyTPOszQjgycQK1+dKNe98x/V4rH5zhLvxTRkmtC4Z88epyd7vHurVq3sm6+r6hvmAbhuKG2qAqF0TyBIDiEqAtUhZHqDkAnUTrUhE/WmPkOm+bwZ+nm0Nkxl04vPo4RMNASxCJkx/XRhAqP5K5DbzDOcfvGLX0Ttm9bUAyYAAABixwRGM0quLo3Po0Dd8CdsAAAAIAYuznpYc4qKqGKiySNkNgCJw6aosGgBQ2UBAAAANHqETAAAAACAZwiZAAAAAADPEDIBAAAAAJ4hZAIAAAAAPEPIBAAAAAB4hpAJAAAAAPAMIRMAAAAA4BlCJgAAAADAMzENmV9++aUOHz5cp3by5ElnbwAAAABAQxfTkPkf//Efys/Pr1PbvXu3szcAAAAAoKFjuOxZ82tTYZ7G5uQE2sRF2uKsAQAAAIDmKqYhs0WLFrrwwgvVsWNHu7Vr104JCQlR+61bt7b3qZFvhWa6Yc+0B2dq9T5nXT3wrZhhnSdXLxX7nCVe82nljMBreWRReHQNnNt9rQ/quVX1+EIBAAAAoI5iGjLPnDmj+++/X1OnTrXb4MGDlZubG7XfpUsXe5/q+DcV6tG8ZdqZkK0JRUUqtNq8cZfoz0tWqV7il3+T/vjWDinkfHabM1oZzibnxA7MeXrVOkUkEzBnfDE0cL5ZI9RD5dq+9HkVUUIFAAAA0EDEPGSWl5frq6++stvp06d14sSJsH7d+FS8pliHlKCsMRUhLz5zrJ55+BL9Kc+t+IU0Z1hreEUwR7kzQ0NpxFBYu020w5x/e4k+8sUp9TuttDpincsOviH7BquRVkBdaK4pOLTWrVhW7O97t8QOzDkjegYWhEgcNkUvjHZeZeJ16mtvUq7SA1QzAQAAADQMMQ2ZZqbYXbt2qaSkxG7Hjh3TJ598EtavE9+72moqfglXKz2yjBifqTGzilRYMEEDEq2+W3mcM1opVsB8bNkOa9GkQOVzQpbity3VjGDQPK7Sgz4pLk0j8mfpnpC8d/zgQSvUlmv7W/uVke8ev0zF8wNDdE3A/OXcYp1yjv2cFRbL1s2v9bBWEyTNNfZ2+jWLU1LnFOd7AAAAAPhmxTRktmnTRr1799YNN9xgt/bt21fq14V/T6kV+OrKp/dKrGRqBchBtwaSaXzmncq2gmT5pyX6e2gWjEtWcpX5LU6p3x+lwWZdfKr69rZSbPkBlfr82l7yoV1ZTc8IHDvxunR7WOvukg88Hb7rW/Fbe0htXNpg3RIZsAEAAADgG9Koh8vGd0lSJ+f7WvPvUWlNydTZJq5zkkwRtHbMsNX/DVRAVabi2c5wWXO/aGADz5hq6bPLAveFjps8RNQxAQAAADQUMQ2ZX3/9tT766CO98847djty5Ig+/PDDsH6dtE1WkkmBZZtVEnJPZLXiuyiphmTq3nfZNb1PpQDXNjnZCrblOlgaObOsGbb6LSUl22NzlTWpqGJSIKsVeBQG3eG4h8zwX68mGwIAAAAAj8Q0ZJ533nnq16+fBg4caLeLLrqoUr9O4jN1x0Bzw2SZiheGPKfSt0IvhE3kEypR16absbHbtPaNwB7+Ta9pnSkM3jBYg1OcIa9xV6pvn8qxMD41Xb2sHFm2eUvgfL639adinzNsNV6p6b2tEFpmhd7apt46sF7XPAImAAAAgAYspiHTPPPy6NGjOnz4sN38fr/Kysqi9s1EQTU9J9NMlGMm7ulUtk5z3Rldp36gXqOiVw4Th03UQ1mJKls3297+YWeinhdGX6VNhdP1UvFJZY2fHLjnMpKZUOiJEerhni9vmf6RNlJTnEqlmdn2cXuyn8CxAy3ieZbBa3UfVWKG1wa2cWe9NRMTBTY1xzHrdmrTa28Fht6Gvlarhc+MCwAAAADfnBZHjhwJexBl7sv5evGBqUqIr9skPLWxZMkS7dmzx+kFZptt2bKl3arqG6NGjbKfl9mUmWD52LI9Sh05TY8N8WJQLdB05S9foBu7ZajfFWnOkobB/JFs/PjxWrx4sbOkYfve7HHaMP33atkipn9rBBqdW58dq8VjZqhd3AXOEsTCx6V7tOS9lZp93+POEgBe+epEue6d/6gWj813lngvpp8uTGCcOnVqsD355JOaNm1a1L5pTT1gAgAAAEBTwp+wAQAAAACeIWQ2AOa+0sKiBQyVBQAAANDoETIBAAAAAJ4hZAIAAAAAPEPIBAAAAAB4JqaPMAGAc8UjTLzBI0yA2uERJt8M8wiT+wunOj0AXuuR1KVeH2FCyATQqBAyvUHIBGqHkAkAdcenCwAAAACAZwiZAAAAAADPEDIBAAAAAJ6Jacjcv3+/du3aVad2/PhxZ28AAAAAQEMX05C5fPlyFRQU1KmZYAoAAACggdq1TD9/5P/VzrDpRNGcMVwWAAAAQN2ZcHnP3Zr03hmltJA2z/mh7p5E2ESMQ2aLFi102WWXqXv37nZLTk5W165do/bbtm1r7xOdTytn5GhsTnjLnblK+5wt6sy3QjMjjjc2Z6KKtjjrAQAAAEjdRug3r/6X/k+rjfrz7le1L+MV/dfs/0s9qvv4jmYhpiHzzJkzGj58uP0sOdNuuukm3XvvvVH7l156qb1PzRKUNalIhUWBVjB5iFKcNWctIVsTzPEKJmhAYpmKZxM0AQAAgCCnkvniqf66qes9StnyIyqZsMU0ZJ4+fVpHjx7VoUOH7Pb111/ryJEjYX0v+DcV6lFTfXw7tCp5liExPlV9eyda35Sr9ECgPupbMSOkyvmgnlsVUjcNq4QGzulu/8iiwAUE+hX7hR8vshLr16bCvLD14eesvN49T837AgAAAGfJqWTOvraF9lnB8uqJ/0klE7aYh8wvvvhC+/bts9uJEyfk8/nC+t4pU/HCtepsKpyzRqiH3V+kcy1GmkA4/YOr9bRdNZ2le3qWa/sflmi1yW0mYOYt0063CjprkA5Y59x3820aYOXUsg2rtXrnJv3xrR1Swg0aNCTFPt5jy3YoIXuSXYWdNyFL8duWakYwaB5X6UGfFJemEflFem5ET3tpgAmR0/VS8TGljsy39zfry9bNDgmaFmffStcLAAAAnCsTNl8gXKJCTENm69at1a1bN6Wnp9utXbt2lfpeSsgeo5wM65vE69TXZLOyzSqpa8r0va0/FZuQd6X69klR4rApIcNx2yop2UqP5QdUam3ie7dEOxWn1MG3ypzW2liT54xWRnym7hhoXUD5Ni3Ln6v1Pncbn94rsQKnFQIH3WrvofjMO5VtNv20RH83QdC/R6WHrK9xyUqOHAPs366tH1ondgKrkegG2s1bogfqqo4FAAAAAB5oksNlPVG2TnPN8FJTmTSVwGmTNdgEM/8mLcxzh57m6iUTQG1+7bHTYNXc8GdzQ6EbIKtz/KAdYOM6J8ndPchZVyMTbqea683TqztCQjAAAAAAeCymIfPUqVPau3evdu7cabfjx4/bw2RD+/UqrrOSKiW1KNwhr6YtcAKmmc12zlytP+YOPy3QQ1nuAePVJamT831lvrfXaL0bCK0Au9gMZ43vomp2sfn3lOqQ4tQ1vU/lyYzaJtfu9QSHy5rrbaftS59nEiMAAAAA9SKmIbNNmzbq3bu3brjhBru1b9++Ut9LZesWBsKU711t3WF9dYaJBiYGOsdHnRjucFVH4nXp6qFy7S75IHBcU/V8apG2+Fbod8vMfZhWcLXvD7WuzdyfuS9R16YHhtGufSOQ+vybXtM6+5bNwVaw9al4TbEOOUN1K3EnJSrboLXuJEJ2mKVaCQAAAOCbEdOQaZ55uX//fu3atctuZhKgf/zjH1H75eXlNTwns3oJmd10YHbIkNdHR59j8ErU0HFWSHSHn+b+Vvu69FGwGJk4TA87E/dMN8Npcxer5fAf6tRrb1Xcq5l4s75nqp9OsEwcNtGuhprJeswQ3IfnFutU9iS9MDpFK2eY4a3WcYPDXXPsSYKsBdq+dKoeWfSxMsc+EZjMx+oH1u9R6shpesy5R9MW3N8M7zWTBD0auFcVAAAAADzW4siRI2FPssl9OV8vPjBVCfHeVhWN5cuX67PPPnN6su/BbNWqlVq2DGTdyL5x55136rLLLnN6tWMqlb8MhrXGmqZ8gZBZmq0JZvIgZ6nNmcX280b9+oCzk798gW7slqF+V6Q5SxoGv99vP9938eLFzpKG7Xuzx2nD9N+rZYuY/q0RaHRufXasFo+ZoXZxFzhLAAA1iemni+HDh9sfwtw2YcIEPfTQQ1H7ptU1YAIAAACInd27dysvL8/pATEOmQAAAACApq1Jhsz4zLF6vqiokQ8lTdTQKUUqjBwqa5jnbzb61wcAAACgKaKSCQAAAADwDCETAAAAAOAZQiYAAAAAwDOETAAAAACAZwiZAAAAAADPEDIBAAAAAJ4hZAIAAAAAPEPIBAAAAAB4JqYhc/v27dq4cWOd2pdffunsDQAAAABo6GIaMt966y0tXbq0Tq20tNTZGwAAAADQ0DFcFgAAAADgmZiGzBYtWig1NVX9+/e3W9euXdW3b9+o/QsvvNDeJzqfVs7I0diciSra4i5aoZk51rKJi+QuAgAAAADERkxD5pkzZzRw4ECNHDnSbtdcc41uv/32qP1LLrnE3qcufO+WaKf1NeHqDGUEFgEAAAAAYiSmIfPUqVP6/PPPtXfvXrudOHFCX3zxRVj/3Pj0XskO62uC0jPciOlWO932oJ5btc9ZZ/Fv0sK80PVWe3CmVodsEsq/qVCPhmy3fG1IP6Q9ssjUUf3aVJgXsjxQcQ07Rkh7ZNEGZ/uQymwId7/AsY0qKrkAAAAA8A2KeSXTzBZ7+PBhu3399dc6evRoWP9c+De9pnVWxoxLG6xb7IxpQlieXt2RoKxJRSosKtBDWe20femvKoLm8YMq9Zl9Rurpolm6p2dgcVVMyPvl3GL57W2LNG/cJdr4fmdNNN9PyFIna5uE7EnWeYr0wuirrMA4XS+3vN/uFxZM0IDEMhUvXKSPM8fq+Sr36Wufp3ZMgP219dqcLgAAAAA0AC2OHDkSNh419+V8vfjAVCXEt3eWeKegoEC33XabunXrZvc3bNigHj16qFMnE7Uq9832gwYNUvfu3e1+ZW6IdLoWExanTB6iFNMx92fmLdM/qll2kRMcT1lB74XRKYHj7UnTiGmTNdjewWVC3XS9VHzSCqxzlBMxFtcNoIHjVDVQ17nWkGNX3qf25/hVn/ft7w/Za0yIrrw90BTlL1+gG7tlqN8Vac6Sb87rr7+uFStW2N+bP6IdOnRIiYmJdt8YNmyYfQtAQ3RXwc90ffd0XdAmzlkCoCqvbXlbi8fmq3OHit9tAOF2796tefPmadasWc4SNHcxDZnmPz5z32VKSiC97dq1S8nJyYqPjw/2+/TpcxYh0wlZKYEAuTMhWxPmjNZVIZXHaCEzbsUMPbZsj1JHTtNjQ+KqCZkR56pNyHTOZe4RDYqrTcj0BbZ1uME5GIi/M1R9dq7UxouH6junV+qtKNcENEUNKWQuXLjQDpou80eynTsrfuPHjBnTYEPm3/d/on+dOrfRI0Bz0fvSbjq/9XlOD0AkQiYixTRkzp07155dNikpye6b+zM7dOig888/P9jv16/f2YfMDDekHQuExv4lNVQyv6tSs/27FzvBr3K1sUIdK5nmXs/pc7X+ZCDwZpxVJTP89Tx0yVp7e7t6aYfVn+j04ujBF2iKGmrIvOyyy+z/c83Ly9P+/fvtZQ05ZAIA4BVCJiLF9J7M1q1b20Nl09PT7dauXbtK/XMTr9T03uqkcm1f/Ya2JF6nvj2l8m2r9aY9MY4V2l57SzuVoOsGW6HT97b+VOxT3JXp+nZYoKyKe+wylWxxZtmxAusLM1cpyhxB4Xzvaqtn90/GKfX7oyJCMIBvinnc0ujRo3XeeefpBz/4gbMUAACgeYppyDTPvNyxY4c2btxoN/NXj61bt0btm0mCqn9OZmXxmXcq20zeU7bZCoOJGjrRmXBntpmFNbeiSugOrbU2Ld+2VNPtGV5NVdBeoGVTK8/YGp85Vo+P6KmydbPt2WDHTv1AvUY5FdJI8ZkacW+WOpWt01yzbd5atcusZlahMKHX61NC9ng9NqTiLJF9AN+sm2++WZmZmcHvs7Ky7O8BAACao5gOl33zzTftR5a4zGyyrVq1UsuWgawb2TfMczXN8zI95wyb/Tz0HkqHz75Ps5QhqEAD1NCGy5o/jE2YMEHf+ta3nKVSSUmJ5syZo7vuuovhsgCAJo/hsogU00rmLbfcopEjRwbb/fffr3vvvTdq37R6CZgA4BHz/F8z8uKVV14Jtu3btwcnNAMAAGhuYhoyAaCpMZP8hAZMt7mT/wAAADQ3MR0uCwDnqiENl/X7/frqq6/s783XX/ziF3rhhRfsvnHBBRdQ0QQANHkMl0UkKpkAcJZMgLz44ovtlpiYaE9U5vZNI2ACAIDmiJAJAAAAAPAMIRMAAAAA4BlCJgAAAADAM4RMAAAAAIBnCJkAAAAAAM8QMgEAAAAAniFkAgAAAAA8E9OQuXHjRq1Zs6ZO7fDhw87eAAAAAICGLuYhc+3atXVqhEwAAAAAaDwYLgsAAAAA8ExMQ2aLFi3Uv39/DRo0yG69evXSgAEDovY7duxo7xOdTytn5GhszkQVbXEWWfybCvVoTo5yZ67SPmcZAAAAAKD+xTRknjlzxg6Zt912m93cUBmtf9FFF9n7AAAAAAAah5iGzJMnT2rv3r3auXOn3Y4fP659+/aF9euHX5sK8zQ2x1Q9wyufbtXzkUVuKTSyOur2rTZxkdyt3P3G5jyo51a59dI6nMe/SQvzrG0enKnVzu4Vx3RayPl8K2aEHDfQKq658r6VzhM8lnuNznVXWl9xrsrvidNCrrkS3wrNdLczr3+Dc/zgMqc556vyut1rClluN2ufdyLfx1C1ei0AAAAA6lMzuCfThKrpernl/SosKlJhwQQNSCxT8cKKIFLBbPtrvbrD6Rr+PSo95Hxftlkl9k5+bS/5UIHF5TpY6rOXmfO8VHxSWZOs8xTN0j09rfPMryaQhTBh65dzi+VPG6mnzXXOGqEeZes0NyQwSQnOsQv0UFaiytYttEOsve/ilrrP7Bexrq7MsZ5dFvoGmICZp1f3pGlEvvP+tdumZc9X8f6ZgJm3TDsTsjXBfg2DdGDpB7p6lrNforWNu27OaF0V7bo/ztSYKPv0sU9UO5VfCwAAAID6FtOQ2bp1a11++eXq0aOH3dq2bauUlJSw/tmxwtzsiorXw1ZYc3OhFK/MsbP0wugMp9tFSZ2sr+UHdTAi/Pk3vaKlxSYwhjh+UCZDxn0rU9+2wmnJFpPqtmvrh8eUOvRW9XA2CyyzNky4Wun2qRJ1bXpP6zyfausHNaVMN7Qm6LrBQ5RiFiXerO9Zoasi2FYhrrOSrE3iM8fqeSuABV5hvLoEXqBKD9Qi3Ybyb9Ky34e+dxbfu9pq5bS4K9P1bXNh8anq27vq6/K9W6KdilPq4FsD15I4TJOD11WZZ9ddlapeCwAAAIB610SGy7oVvkCbNyFLJq4EhQ3hzAuvVLpO7LBDiT9tqAZa2TBSXJf+yrLCVdnmLXpne4k+8sUpKamjva784AHtc8KoTPXROddjVVTRytbNDlxH7lytD+bZ4yo9GBFuq+SG6Vy9ZIXhhBsGa7CdSMOHs1Z13orrCuxb2QntfOX3Wn8sTYNvrXgD/HtK7aBWvm2pple7v197giXf2qrFdUcRfB9NqzR8t+rXAgAAAKD+Nf3hsuY+vV+HDOG0h7E660KU/XWlHUruHHWLAtExIBCy4pScdLlS03urU9kGvf5fH+qQqVj2T7YrieUHSuVrG/g+OLQz2BbosSF2ErQlZE8KLHeHgtraKik52KlGRZh+bkRPK2jN13OrdjpDfMPXVRK8rsCw1ErK/qrVxceU+v1RGhjyBsR3SbIDe5w7jDfY5ignrETpViJryx2aXMN1R+G+j/YfFMq36bUlITMJR3ktAAAAAOpfExkuWwfO8M/K4uxQEqgMVjh+8GBwyGV8arp6JZbrs/0+JVydoQx36G1gZdRhpDWLDwRYlend1U5Y8r2tPxX7rHA3WLdEG29aJZ/eK6l9RTBUXNr3dW9IILYlXqe+VvYr/7REf69hFGvidenqoXLtLvkg8BpMwH+qqntfq3L2112VKl8LAAAAgHoX05Bpnnm5ceNGrVmzxm4fffSR1q9fH7X/z3/+s4bnZNZCfKZG3JulTu5w0by1apdZuWKWkD0+rOIYLk5Jna11wVCZoPSMkORn399p7v18IjDZT8j9odXOxBrC3J/4+IieFcNS85bpH2kjNWWyc4+mreLYZmhp4Jp7KPNH9wYmM7LX5emNdpkV9
Ссылка
Юлия Калиниченко
22.09.2023 17:11:44
Добрый день! скажите, пожалуйста, где может быть ошибка, когда в сводной таблице на один столбец даты не ложится сумма из Выписки и Остатков? создается 2 столбца Сумма по полю. Заранее спасибо!

[IMG]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAA4wAAAJUCAYAAABe0KhUAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAANN5SURBVHhe7N0JXNVV/j/+l+YC4oLKpmJWKqImkEuNTYpLKS5Z89VRa2xcpsZxT2kxTc1KM0vNDf/NFEpjjZH+2tyyUtHKzFzAVKBMUVEQVBARzO3/OedzPnfjXrgXwcvyej4e58E9n+1+7nXGfHHen3OqZGdn3wQRERERERGRjarqJxEREREREZEVBkYiIiIiIiKyi4GRiIiIiIiI7GJgJCIiIiIiIrsYGImIiIiIiMguBkYiIiIiIiKyi4GRiIiIiIiI7GJgJCIiIiIiIrsYGImIiIiIiMguBkYiIiIiIiKyi4GRiIiIiIiI7GJgJCIiIiIiIrsYGImIiIiIiMguBkYiIiIiIiKyi4GRiIiIiIiI7GJgJCIiIiIiIrsYGImIiIiIiMguBkYiIiIiIiKyi4GRiIiIiIiI7GJgJCIiIiIiIrsYGImIiIiIiMguBkYiIiIiIiKyi4GRiIiIiIiI7KqSnZ19U70mIqJK5k9vDFOviMhdfnxptXpFRFT2MDASEVViIjAefuML1SOi263NSwMYGImoTGNJKhEREREREdnFwEhERERERER2MTASERERERGRXQyMREREREREZBcDIxEREREREdnFwEhERERERER2MTASERERERGRXQyMREREREREZBcX7iciqsQKW7g/MjJSvXLeggUL1CsicgYX7ieiso4jjERERERERGQXAyMREd0mWzHtpQFo89J8bFFb8MN8OcLSZtVWtYGIiIjKEgZGIiJySJSYGq179+6F9otjS/J38ufjQT3kTyIiIipbGBiJiMhNtmJ7kvj5ELo9KDdojFFIo03Af46qXca+BashT9NsWaUfN+0H2/NUE8fKUUztOj+sxiDTPsvrmq9TYN9Ry3NEU6OjtttNI6RJ+M8Ci+PEli8nyGMGfblV7bNt2rHG9eyNtHIUloiI3IiBkSqsQ4cO4eOPP3bYxH4iKtz69etNzZm+K5K+/BSfaT/bPPgYesktIvS9o217CO+88QUOv/EWJvukYNF71uHOvh6YK895Fo+Lrs9gfCr6kcPQSu7XrvPlbvR+Wtv29GC0Ef3P9OApwuK/G74lJ//RzzfvM2n1rNr/AnqJcPdeLA4b2x59SPsw72iB0OoMO5rgmUhxDfG5RN/4nNo15X4iIqKyh4GRKiwRCGNjYwu0HTt2yJ8MjERF69+/v6k503fOd3j2pQH4yw8pWlh8C2sf1SMdfvjZJkC2wjOdtTCmBbivDhcVxorW5sHxeKa59qJ5J/QWgS1zN3ZoQbTXiC/M96CFurvlvtPau9qXdHg3Dms/TWW0D3aUIfVw8h7rkElERFQBMDBSpVG/fn2MHTsWM2fOVFuIyD3UyNqjD+HwD8+bSi2Tzp2UP4uUGYu/qHLOZ0sioVmVlz6PRZlquwMp5/Qo+dmXxjliVNSWHorFfhGMnZb0jrqmaBaTAxEREbkJAyNVeE2bNsWwYcPw1ltv4eGHH0bVqvyfPZGzbEtOi+q75MHH9NLMpE9lyWmrhk317UUxyk219o4xMFgsTdGs+VZME+Wlpmsa5aKONWvYTP58/FH9HkzNVP4qGOWmX+DTB/XjnWKUucqyWS10WjyvSURE5A5cuL8S+O6777BkyRJcv35dbak8atSogTlz5qB5c1GHpsvIyMDo0aNVr/IZOXKki+WDVJEVtXC/5eynIhRa/m/Htm97fEGWzyjqz+2JCWHkCJwISiNgs19MICNG/Iy+Ol+EOxXOxPOHYpRRhLe5cuKcgsfISWO+FLOxNsPkp5fiGahnEOUxjRFjebzxfKJxD5bPK45QJaj2tpnY3rP5M5rLbwseU+Calv2gn/X7t/t+VN6J0WQu3E9EZRkDYwW3a9curFy5ErNmzUKTJk3U1spBPKcoJrcRI4zh4eHo1q0bGjRogLNnz+Jf//oXhgwZgsGDB6ujK4fU1FT5v4XHH3+coZEkdwfGAttMgc1g59hiBsY2rcTkNN+pa1tc1xQohWZ4XDvps6Sm1vdjG9asztHpgRC3FhjFa4PxGYz3YmCskBgYiaisY2CswE6cOIFXX30Vs2fPrnRhUTACo+HOO+/EqFGj0KhRIznCWBkDoyBC48svvyyb5cgrVU5FBUZXFXc9xlJlBEbLCXaIyggGRiIq6xgYKzBjWQkRGisj28BoaN26NY4cOVJpA6MgJv4Rn79t27ZqC1VWhQXGCoOBkcowBkYiKus4+0cFJsJAZQ2Lgvj8IhDatnbt2smfDEtERERERIXjCCNRJcQRRjJUihFGojKMI4xEVNZxhJGIiIiIiIjsYmAkIiIiIiIiuxgYK7C8A9GYMnsDTqo+ERERERGRKxgYKyARFMcP/BvmJ1WHPy5h+2sD8TctOJ5R+4mIiIiIiJzBwFgBeYaNwrJ17+Gx3N34KWELrvRfhw9n9UMjtZ+IiIiIiMgZDIwVkD7C+DQ+93oA94f0Qs31HGEkIiIiIiLXMTBWQPoI44d4odVVpKM2us3gCCMREREREbmOgbECE8FxoRYUm6o+ERERERGRKxgYiYiIiIiIyC4GRiIiIiIiIrKLgZGIiIiIiIjsYmAkqqTy8vLUK6pw/jiEDyYOxMChL+PzFLWNiIiIqBgYGIkqoT59+uDf//43UlNT1RaqKHK/noeBf/8faj3+GJqobURERETFVSU7O/umek1ElciuXbuwcuVKhIaGqi1U3owbN069KuiPQx/gudeS0fPN1/FYM7XRjj+9MQyH3/hC9UrW+fPn1SvnNWjQQL0iqhzavDQAP760WvWIiMoeBkaiSuzIkSNIS0tTPSpvunfvrl4VVBYCY2RkpHrlvAULFqhXRJUDAyMRlXUOA+OOs78g40q26hGRO3X1uxe+NeupHlHRGBiJygcGRiIq6/gMIxERlRpRYmo0Ly+vQvtF245lw4dj1PAliFNbsH2J1te2LdmuNpAQt0R8T8OxzPJrSf4YL4vvatrH+FVtIiIiKgoDIxERlZrp06eb2v33319ovzjiEvbKn+1DusmfREREVLKcKkkdGtQDntVrytdEdHvsSj2ExKwT8jVLUslVZaUk9bXXXlM9YOvWrejRo4fq6f3+/furnn584SWpYoRxJfahA4bHTER4gb7lMYYmiJg+F4ODxGu1r0lfvDR3CFpqW8RIXIyWOduPHAmstDxPEcf2SscbK9MQMTIUCSs34rS+w+K65uvoLPaJUb05xjmCulfb7R1GInqiCL3JiJ02B5tTzZ/p14+n4Y2NqWjcdyRC4ldq++QZFiw/v878uWIw3sjSxnva+fw6O/dtuq+C1zSfa/H+Fp+rcd/peH2I/gU5/z7G53fiOxQvxQjzStOFdRb3XOBcp75n833fDixJJaKyjiOMREQViFxWY+BAPDHzc6RePYIPpujrMf6UoQ64zX788UdTs9e/Fb9+vEUGvMZ9I1RYsgyQMYiOmY6IJqnYPGcaYpPlAYXohvHynJFoL7oiVIm+ClaAdp2V8QiZrm2b3heNRX+VXtopwtDX/tO1c43zzftMRFCR+7VwYhmSxLaRHYC9K/Hyx0XdZGMMniuuIT6X6Buf0zosOsup+1ZEmDIHPiEZ6ab5svbioCp9/XV/vCmcnU7XX+lhUQRA497Fn4lFWXFhjO/K+POQ97kXMZZlyRoRYsXneKmv9sVo36UsxZXnpuMReZ7NPiIichoDIxFRBeL1yFSsW7fOuq15Hff7qgNuMzGiaDR7/eIRgWF4wdGg7Qk2ATIIg3tpYUwLQgn7i0yMRWrcd4Q+4hV0H0JEYEuNh7hs+MQYixGpxvCT+9ItRsSsGaHKVEbbLUSG1NPx+0v82cJ9K/VnGWWzGqVz4b614BWjfdfWTuOs2NSkA9pr5+1LkAkN++PFn0lfPXRL23FQBM0mobhPvlUQ7gsVb2QOmYUxfVe9jODeDb1F8Cv0/Cbwa6z9CBqC1y3CdEv/APkzLf3W/7dARFSZMDASEVGpuXz5sqnZ6xePGlkb2QGnN84xTXjzq3nIq3CpG/GGClHWo2bFJEayjFA2XJQ5qu0OnE7XDzCHOTulsCoUi/0iGBeXMfImmxwZteDUfacjdpU+whchsretgBD0FgFwbwLikvcjQbtGgL+/vi8tHb8mp0P+qVh853Y/z96Vdu/D+K6KYnyX8todeunBXiNGN/Xras22dFUqme+ZiKgiY2AkIqJSY1uCatu/Jd0i9NLMvVtkyakxglQkU3ljDIbbC0FOC4B/0HYssyqZNMpFHWvsrx9gFeZEM5W/Cka5qSqlLHFO3vfejfrzhCOGQMVAnQqCjf0bo+V9oVoQ3YuvV4nRwA5o181itDLIX/uWNBbfudFMz1YKppJd6/swvquimL5Li/Jeo4zWal8Bpf09ExGVfwyMRERUamxLUG37t8Yob0zF5s3bzaWdGzer59uSEbtFjCp1wCMlMInJ6Y2r9Gch1Ugamvhbj9gJxr5C6AHLKOMsGcZIWrGfzyvkvk2luJZOW5SuqhLd06lidC8E4dqfizm7d0M7WRWsl++6yvRdbTGerdyOr8RIoBZAe1sGTicYM+o65zd8Ml18py9j7VHgaOx0+f3O/ETr/BaLGWJU8uVP8Ls6moioImNgJCKiUnP+/HlTy8/PL7RfHC2H9NKflxMlkWLiGll2aZQZWs+CeasadwhAwhztuvJZQO26ckRQe08xcmWUXM6JR0CHIkaqxLN1aiTMVC6ptaInvSlJTt53h5GFzhga4C/2mQOi9fImaRCPC4ZPNCa6MX9Wq7U0C2N8V6aSVutZbg2m8l5RdqruueWQEXK00tgXo/2ZmZ+tJCIiZ3FZDaIyistq0O1QmstqzJkzR73SXb16FdWrV1e9gn2huOsxliq1dMPtXm6BKgcuq0FEZR0DI1EZxcBIt0NpBsYKg4GRShEDIxGVdbcUGKOionD06FHVc86YMWPQokUL1SMiRxgY6XZgYHQCAyOVIgZGIirr+AwjERFRYbpNlLNoMiwSEVFlVMYCYwY+WTFA/rbNsvX8pOAKVeWX+TMW/FyXsPvjZyrwZyciIiIiovLklgPj2LFjsWDBAtkGDRqEadOmOew3b95cnVWUhnjmyS9w+I33MftO4My+NzFu60m1rxw79zn+9dI/MEuvMrQhguSTGHngIro/slyWiInP/6/MpVh0UB1CRERERER0G5XxklRfdGsZol4LxgjcSDshyhi5U/tkODOP1JnarFn4f6e1K8WvQB+tbx7BszlfsLqG2p67B2/N0/pz/g25opNxjG1ftfvf/RJG1M3Yvwc7avfHOz0tP5PuUvxaRGtBsvZdwzC1R1O11Rd/HbMSk9upLhERERER0W10S4Hx2rVr2LVrF9avXy/buXPnCu1fvHhRnemsDGz/NUH7WQstfI0Q5Zradz2Dr8Ro3cszMNLhnCEiiE6zHvkTwe/t92XA+684/7nHkfSFCoUWZAiEJ7p37oMO4pwl+9Brghgd/AJxWjC8dHw15qnRUd+HX8fh6f/EfbJn6RIOJe5DinadTi3DULxPSkREREREVLJuKTBWq1YNnTt3Rv/+/WVr2LBhof26deuqM4tyDv/5SIzQ6eWbte/6PwwqxVG2S/H/xSsH0lVPZxUExYaGj+H/08KefG2iAm2NYPQM1mKeOGb2bPxfY32vp28TNEMeEs9l6BscysOJ89bvT0RERERE5G5ltCTVeIbxC/w0tA8aHv8Pehsln5IRKPV2SxPDXD2MFZs24dxdgzHmTrUNl/D7uSIC3KX1eEoE2vP98V9TSLSetOb+NZuQIg8uiifubOCvXhMREREREZUNZbwkFajdoiN6iFLSP1KRclrfZg6UH2FlmL+aFOeM2ueaMwdjsTLvPkx9tDcC1DbtXXFPwyICnCxVfR+zG2jBUT0XmfHNPKtJa0TYbaYOL5zxfnnY8+sB0zOPRERERERE7lRGS1LNLv32M7Zma5GqcUd0UqWeBYlnHBup167yRPfwp01lpAbf+zqhq2WAE5PdLLV9htEXfR7UQuEf+7H8+4JLZOjPJTrHt/Nj8hlLy2ce9RHLFzhLKhERERERuUUZLUk1l5yKss5zdz2DdaMftZgMxthvLEPxarFnEm3U/kUsN81KaqHhY3jbKIcVJaavR6FaN9tnGM0joGd++Rw720zC7DvzsO3rcfLeJpxtiV4WE+1kfPOy/Ezh34qJfMRyIa9o/SH6kiFenfD8VLGMiHG+/vmmVR3KWVKJiIiIiMgtqmRnZ99Ur63sOPsLMq5ky9dDg3rAs3pN+dpSVFQUjh49qnrOGTNmDFq0aKF6ROTIrtRDSMzSp+7t6ncvfGs6nOaXqNj+9MYwWUJPRO4hfkH840urVY+IqOy5pcBIRKWHgZFuBwZGIvdiYCSisq6MlqQSERERERGRuzEwEhERERERkV0MjERERERERGQXAyMRERERERHZxcBIREREREREdjEwEhERERERkV0MjERERERERGQXAyMRERERERHZxcBIREREREREdjEwEhERERERkV0MjERERERERGRXlezs7JvqtZUdZ39BxpVs+XpoUA94Vq8pXxPR7bEr9RASs07I11397oVvzXryNVFJ+tMbw/DDy6tVj4hutwdfH4YfX+L/B4mo7GJgJCqjGBjpdhj74Rz1iojcJepv09UrIqKyh4GRqIxiYCQiIiIid+MzjERERERERGSXWwNjTk4Ozp8/71K7du2aOpuIiIiIiIhKk1tLUqOionD06FHVc86YMWPQokUL1SOquFiSSkRERETuxpJUIiIiIiIissutgbFKlSqoU6cOGjRoIFvt2rXh7e3tsF+tWjV5TpFy92Jl5HCMGm7RJq3CAbWbiIiIiIiIiub2ktTevXujefPmsr9r1y4EBQWhYcOGdvvi+F69ehVakpq7NxqvLInDOe/umLh4BMLExswNmBcZi2SP1hg8YyoiAuWhRGUaS1KJiIiIyN3cOsJ48+ZN5Ofn4/Lly7LduHEDV65cseq7JhNxX2lhEd4IH6nCouDTD08PbgXkH8GWbw6YRiCnrNqOjXPNo5BTVqkxyAIjlJMQw+FJIiIiIiKqZNwaGK9evYrDhw/jxx9/lC07OxuHDh2y6rskczcSkrSf3vch1JQWdZ4BARDjlPlpZ3BK34SsbSvxTePJiI5ZgEFanhR9q2AoRiljYrT9izHc5npEREREREQVnVsDY40aNdC+fXv06NFDtvr16xfol7T8M+nIVK9FIPz7CJEEfXB/qJYYkYX4AxxKJCIiIiIiEipYSWrRPBr5a/GQiIiIiIiIilKxSlI9A+Av0mDWfsTbDBTmpaXhnPbTI6ARHM9544EAeQEiIiIiIiKqWCWpXh3waA+9tHT35k2mZxXFzKlvxiZZlKAqWdvwgZzoJhM/xYuHHz3g34hTqBIREREREQluDYxiTcWLFy/i/PnzsuXm5iIrK8th/9q1a0Wuw+jTbxqWTgyH15E1mKlmOZ2wJA65rYfiVWOZDYN3B9xzepF2TCTWJnkgeOjznNyGiIiIiIhIces6jKtXr0ZKSorqQQbCO+64wxQKbfvCsGHD0KxZM9UrJrFsxswl2HnNYq1GojKG6zASERERkbu5NTC6DQMjlQMMjERERETkbm4tSSUiIiIiIqKyq3IGRq8OGLkgBtEcXSQiIiIiInKII4xERERERERkFwMjERERERER2cXASERERERERHYxMBIREREREZFdDIxERERERERkFwMjERERERER2cXASERERERERHYxMBIREREREZFdVbKzs2+q11Z2nP0FGVey5euhQT3gWb2mfF2SUlNTkZ+fr3rOady4MTw9PVWPqOLalXoIiVkn5OuufvfCt2Y9+ZqIiIiI6HZxa2CMiorC0aNHVc85Y8aMQYsWLVSPqOJiYCQiIiIid2NJKhEREREREdnl1hHGFStWIC8vz1RieunSJXh4eKBatWp2+6KEdeTIkWjevLnsO5S5AfMiY5Gsuibe3TFx8QiEqS5RWcYRRiIiIiJyN7eOMN68eROPPfaYLDMV7aGHHsKTTz7psC+eXxTnOMuj9VC8GhOD6AWDEaS2ERERERERkXPcGhhv3LiBixcv4ty5c7JdvXoV2dnZVv3iyE1Jxzntp0dAIwTqmwoSo5DDh2OUamPnbcIpZGLjXPM2Uxs9D5tPOTqHiIiIiIioYnJrYLx+/TpOnjyJ5ORk2UR56qlTp6z6xZGXliYDo0Mi+E0/iLA5MYiOicH8wa2Qf+QzfLQpH32niW0LMKiVdpxHawwWx7w7FREejs5hZCQiIiIioorJrYGxevXqaNu2LTp37ixb3bp1C/Rdl4uUdDm+iAB/H32TLZ9+mCpCoBp+9AwIQEPkIy09U99gT3HOISIiIiIiKscqYElqHtLTtBDncTdC2jkqSM3F3uhIU2nphCVxhY9ISsU5h4iIiIiIqPyqeCWpmbuRkKT99AhAgIO8mLlhMZbHXULw0DmyvHTpxHA0VPscKc45RERERERE5VkFK0nNxd4vtiIZHgiOeNjJ5TNykRh/yMXRwuKcQ0REREREVL64NTBWqVJFrq149OhR2TIyMnDixAmH/fz8fHmOfaJkdCaWx4lnCvORuGa6qXx0lLEmY9Y2LBk9Dz+H/hODWhnHjMX7J5vhXgePOxp8+rl+DhERERERUXnm1oX7P//8c5w+fVr1gD/++EOOOhqh0LYvDBgwAE2aNFE9Syow7vbF4BnmyWnMitpPVLZw4X4iIiIicje3BsaSxcBIFQsDIxERERG5m1tLUomIiIiIiKjsqkAjjEQVC0cYiYiIiMjdOMJIREREREREdnGEkaiM4ggj3S5nsjPxl6hnVY+ISlOjer74dOwi1SMiKvsYGInKKAZGul1EYHx1/bv4cMybagsRlYar164h4u3RDIxEVK6wJJWIiIiIiIjsYmAkIiIiIiIiuxgYiYiIiIiIyC4GRiIiIiIiIrKLgZGIiIiIiIjscmtgTE1NxdGjR11qeXl56mwiIiIiIiIqTW5dViMqKkqGQFeMGTMGLVq0UD2iiovLatDtwmU1iG4PLqtBROURS1KJiIiIiIjILreOMK5YsUKWmHp6esr+pUuX4OHhgWrVqtntixLWkSNHonnz5rJfUCY2zo3E2iRvhE9ejOFhYtMGzIuMRbJ3d0xcPAJiE1F5wBFGul0KG2E8f/485syZo3rOadCgAaZPn656RGTgCCMRlUduHWG8efMmHnvsMVlmKtpDDz2EJ5980mG/cePG8hxXZO6OR7L20/u+MIZFIiIiIiIiF7g1MN64cQMXL17EuXPnZLt69Sqys7Ot+rcmEz/FJ2k/vREaZsRFMQo5HKOGG2005m86Zb1v9DxsVpsyN8yVx01Ztd3mPNXEsQc3YJ64zmdbsDLS2Gd5XfN1CuzL3WtxjmiTEHPAzvZJqyA2azuwNzrSfJzYsjcaz2vHjJ33Gb6W+yzOk818LBGR22V8imdeGoA2b7yH/WpT+tfT0Ebb1mud+MsqHbFR2n5xjE2z3v8PLD4kT7d7TSIiIrp1bg+MGRkZOHXqlGxXrlxBZmamVf9W5O79Atu0vOjROgI9ZV60LFmNQXRMFMaF10bimteswp193ug7TZyzAINaaV2P1hg8R+u/OxURjcT+fCR+ug4ZD89BdNREdPHR+p+tlsFThMWZB+/DqzHG+eZ9JqJkVu5fjOEttbA4cwl2XlPbFgxGUNY2/HveJhR+lzXRetQC9bl8tL7xOVV5LhFRMYgS0wULFsj22muvoW/fvg77xStFTUfcr79oP33RL9jyLytfjB72BQ6/YW5bBtr/yyz9wB58r/0MDOqI+/RNREREVALcGhjFs4niecTQ0FDZateuXaBfPFmIWzQcE5bEIbf1UEyb2geBYnPmbiRYBUgvdBjQA0Fa2Dsef7CIMFY0j9aP48k+2jt5BSOkrRbY8o8h4eAp+PSbhijjHuAJ/wCx7wzSM+WGAnIT43FY22cqo/V5ACFaSM0/Fo9fbvUmiYjKmowf8PVJ7WfdzujaVt/kGkeBk4iIiG5VBS1JVSNrCwbjziNrMFOVc+ampOOcfkDh8o8gdrpezvlCrChpvUVW5aVjsTzOQVJU8tLS5H1mbVukzhGjovo+Mz0Ui/0iGDv1uYiIikFUe6xfv162rVu3ysnKCutfu3ZNnemMHOz6dgO+Ry08/KeIYo0O5uxfh2gtcNa9+/8wsFiBk4iIiBxxa2C8fv06Tp48ieTkZNnEPzpEKapl/5b4dMMjojQzaxe2bDoFr2b+aKh2FcooN42JwfzBov60uDzg38gDGxcvwc5LxjWNclHHPAMC5H16d58s78HURPmrPkypMcpNY7B0Yrhzn4uIqBhq1qyJ/v37y9ajRw85s3VhfWNm6yJd/AJ/e+lv+Ef8JTzc620s6W76C07JwLurLZ9htHhmUdL3PxC7GVl3j8baf/ZTlRxERERUUtwaGKtXr462bduic+fOstWtW7dA/9Z4ITi0rRam8pG4+RscMEo7j2zGt3ISmFzs/WIrkrXw9UCEUTJafPlHPsNH4lnI3EQkHMrU8mIj+NtmQ2NfIbyCQ9FG5Nz9B9REN0REFVDdAfjwjS+wrcc9+GbLWDWhjSWLZxinjMSfRUD85BV8dkbtNvZr+9odexe9OOENERFRiXNrYKxSpYpcW/Ho0aOyiQlwTpw44bCfn58vz3GFV4cB6C4GCbP2I/6AD/pOEhPSGOWcojz0mnnNxlvkcU9bVPtmOkaNXYKdmd4IHyNGBLX3/OdgBBllrmP/jVPN2hU+IujVASNf0ie6WSJLUvU2tshJb4iISl7plqQC/p0fw/C6wKmDn1mEQRu+D+KRptrPKyeRcl7fZOL7MEaF+gEXv8HKbfxbkoiIqCS5deH+zz//HKdPn1Y9yGcW77jjDlStqudY274wYMAANGnSRPXKiMwNmBcZixOWE+wQ3SIu3E+3S1EL969YscI0++nly5exa9cu9OzZ027f9ni7xBIYC1fiezHC+NLTuE88x7hmMv4RfxaBHV/FloGNEBv1DF45KUYQ38ck8Vyi1TmP4leb/Tn7o/DX2M04YbomUdnDhfuJqDxy6wij5aL9ok2cOBHjxo1z2BetzIVFIiK6RXXQuWc//Fl7dSr5Z4uyUotnGK0CZkF17huIUWIE8uIu7LB6zpGIiIhuhVtHGCsMjjBSKeAII90uRY0wzpkzR/WcI9ZtLN56jEQVG0cYiag8YmAkKqMYGOl2KSwwElHJYWAkovLIrSWpREREREREVHYxMBIREREREZFdDIxERERERERkFwMjERERERER2cXASERERERERHYxMBIREREREZFdDIxERERERERkFwMjERERERER2eXWwJiYmIg9e/a41HJyctTZREREREREVJqqZGdn31Svrew4+wsyrmTL10ODesCzek35uiRFRUXh6NGjquecMWPGoEWLFqpHVHHtSj2ExKwT8nVXv3vhW7OefE1U0s5kZ+LV9e/iwzFvqi1EVBquXruGiLdH49Oxi9QWIqKyjyWpREREREREZJdbA2OVKlUQHByMTp06yXbXXXchJCTEYb9OnTryHMcysXHucIwaPgkxB9QmTe7eaDw/fDjGztuEU2obERERERERFc6tgfHmzZvo0aMHhg4dKlvHjh3Rv39/h30/Pz95DhEREREREZU+twbG69ev4+zZszh58qRsV65cQUZGhlW/dORib3QkRg0Xo5E2I5K5e7Ey0thuMSppbJ+0CvqhxjVGY/4mNW6ZuQHzTNc0n5u5Ya7sT1mlziww4un4foxjjXNN9zF6HjZrJxfYb2+U1cF92TLu07ZZHl/wGIvPb/Pd6d+V7Wczmro/B/dm+x3Zfk7bvvV9WdwTEREREREVm9tHGEUozMvLk+3GjRsF+iVPBJiZ+LDqU4iOiUF01ER08clC3EoRbrSwteJrNJqsbY+JwrhwH+Qf+QwfORM+RPCZfhBhc8S5MZg/uJWT5+r3szzuGsLl+y7AoFba/azQA6FrxLXewNok1RXEfUXG4kTroXhVu6+lE8PhdWQNFpoCpi0PBA+dIz+DOLah2qrLRUr6Oe2nt3av+vdjIsLizA9Q9Sn988tzs7bhg1W/osOoBabvUz9XHLMYwwMd35tXhwHo3grIPxaPXwp8D5mI+yoO57RrhYaFybA48+B98hr695ePxM9WF+P7IyIiIiIiS24NjNWqVUPTpk0RFBQkm6enJwIDA636xaMFrkXmUasJS0S4MHjJALNwRJjqNoO/SEX5aUg75YO+z01FRKC+S+cB/0ZWG+zz6Yep75rP9QwI0MJWPtLSM/UNjuQmIuGQdoz3fVr4ERt8cH+oTEpIOOha4snd+zHWxFm/X+bueCRrn+Gu0HYQt+YVHIo2Wm7L2n9AjZQWg0cj+FtkRcmrA0Yu0EKg6Wv1l2EzP+2M3dFMofB7K+R7yNyNBC0Ue7SOQE/t/Xz6TUPU1D7yGto3D/8A7SL5Z1DUV09EpU/84u/8+fMutaysLHU2ERERuVsFLUk1RrEsRrvUHsmqDDLSekTOVFY5Fsu18OXdfaQpBElZ27BEnqfvN7MuvbQMqXp4dCAvTQ82pusOxwuxljeky9q2SL/22CXYaS8IXUlC7EdxyG3dFz20nKUzRgTzkbhmeuHnOyUP6WnayR4BCLCToa3KQiNjtTBYmKLvTQTB+YObyf3G9ym/BzUqOc0IiValsLZ/LkTkTiL8zZkzx6W2fPlydTYRERG5m9tLUsVC/MZvla9evYqLFy9a9UucCBdvaGHGuzsmmkoY1T5BjpTpQVOUlYqAYn4+UGM6z7okM3PDYi2oXLJbzunVYQiGascaoc9qxNMzQB+tM13XaO/ihT7mVObdfbK+XZbQqo0Wsn7YiJ2XWmPAsJ5ooLZp74xmcvjUXGZqaotHwDIHO0WN7HnfF1bgXPFM4Zta0DXd54LBCFL77Cvq3vQA/kJsugz/xvcpr69d+84jazBTPiOZiY2LtaCpffbBshzYplSWiIiIiIiKze0lqc2bN0doaKhstWvXLtAvdSoE6bTw8XZxnh20lYvE+EMFymCNQGQ14ukVjJC2WsDJ2o/4YteIClrwenyYTTkt4PNAqBbc8nE8/qDD0lBn6SWk+nODRdGPLVyh95a5HV+LkUJTqa4Fn254RIRCe9+ZUeJLRGVG1apV0aBBA9nq168v/2531Pf29lZnFeLsl3hDVBRM/gAJpk1z5C/kIj+IV1uIiIioJLg1MIo1FZOSkrBnzx7Zjh8/joSEBId9MRpZ+DqMTvDqgMFP6hOyyBLQyC2o3cEYYvRB3xHtcGC6Xt4oSkM9Wg/FFON5x0L49PunPtmKLK8ci/dPNsO9Tg10iTD5kj7RjcVzl8YsqM7y7j7GakTSxKcfJqjJZGYa19aa1aipEy5smKt9HykIHvq8dYmuYjuK+sKW2mhvOXJrTyH3ZjzfGBzxsJ2RUC8Eh7bVQncWdm/eg5B/DkZQ/hHEij+3sf/GqWbtHJcAE9FtJ0Lg9OnTZZsyZQq6du3qsD9u3Dh1livO4qcE8SuqBggLDdU3ERERUYmokp2dbXdhwx1nf0HGlWz5emhQD3hWrylfl6Rvv/1WPrNoECWod9xxh/xttL2+INZtFOsxElV0u1IPITHrhHzd1e9e+NasJ18TlbQz2Zl4df27+HDMm2pLyRGPF0RFRclgKOTn52Pfvn148MEHTf0DBw7Iv9sFcfyKFStkeHRIjDA+vxa/NuiJZxf9HSG2fctj5Akaz7YYMuMF9G6id3P2vIfZy3bivN6VPNo+gekvREAdYiEHP783C1E79boRj7Z/weMNdmCN6ps1QPcpi/DUPXsQPWsZvjN2y/v6C/6wuIaZds6YJ3E1Vjv+psX9mxjvfVO/tsjD9j4vlQtXr11DxNuj8enYRWoLEVHZ59YRxp49e5oW5RftqaeewpNPPumwLxrDIhFR+SJ++ffjjz/KJsKimNDMsn9rtED1xTYtGHqiTe+e1mFRBCrxKMCy8Xio1iF8/Np8fJUqT0JeWroWFrVznpiL6LcGoaW+2Q4jsF3Wj41ZhlENfkJCYKR8PbaLqGcQQVE8cmCExY9Qfbj+CMLi8V3Q4Py3iPngd3R8eqH9c9rKN3JOjnb9eRZBmIiIqJS5NTASEVHFV6NGDTmCKJoYWfTw8LDqiwnQikULYu8MH6/C3Aw8F6GPDZ7dnWAdIOt0Qv/uQVpK/B0HD4rEmIMTcpZmT/g3KjieaCUnEQmHtWMbPIhe8vp1tOA31/ReBWjvNWqhGgkUXbXEUF7aGaisegu08Prx/8wjl0RERLcBAyMREZUqEQgvX74smyhBte0X+9l0NYI4b1BTHP7fNDXhjREGC5OHNHGMZyP4FfWsuVj6yMWAZkzAI5tlWWxRZAA2nuf+F97ebB0x8xM/xhoRjvs+XMiIKBERUcliYCQiqqjOf48lzwzEwFELEWd+XPy2K92SVMCvWy881BC48MNX+Cq1Du6US/YUIicFZ7UQ6HFPCO4tYoBRLn1UxOUsiWcj569NRv2eU2RJauHlrjYsS2gb5uHwZx+aSmi1P0zs2rgTl9s+jie6OzGTLJVfZeT/t0REBgZGIqIKKGXtCxj43G40/0s4zGuzukeplaQa6gQjpI2W6vIOYcu38fB7IEQLaVrg+upbfdmNnD1Yvy3ZVFZ6dvsWfHfOE/eEtLMzwY0N49rn9yNerdhx9su3Coz+OaKXx5YQz7Z47G/2JuWhiqIs/f+WiMjg1llSicgxzpLquu+++w6pqbf+pFh54uXlhf79+6teQee/X4IX37+GYW9OQbiv2mijtGdJXb58uWm5jLy8PDmq+Oc//9luX/tvEj766CPXZkm1s+1u21lQ1faAL+dg6tpCVom1vKbJWayf8zz+nzrNPJuqnRlMTdtUHWuDDmjvsxeHqxdyjpjIxnJWVUnNuBpq53jOklpuOTtLalH/v83NzcX69etVj6hsEOvq9urVS/WoImFgJCqjGBhdI/7xtGXLFlPwqCzKemDMysqSgdEgRhOvX7+OatWq2e0L9erVw/jx41WvZInnC6euzbQIeAYVCjMZwqj0MDBSRfb999/jvvvuw8iRI9UWqigYGInKKAZG5xlhcfbs2fI3nGTm7sBY1jAwkjuVVGAkKosuXLiAWbNmoWPHjvj73/+utlJFwGcYiajc27BhA5577jmGRSIiIjcR/w0W/y3etWuX2kIVBQMjEVUIYiIVoqL4PTpdXyzfanRR8EP/6TGI5ugiEVGx3bhxA7Vq1VI9qigYGImIiIiIiMgutwbGPXv24KuvvnKpiRn3iIiocHJ6/oED8czCOJzP/h5L/qWv65aUow4gojKH/78lorLIrZPeREVF4ejRo6rnnDFjxqBFixaqR1RxcdIb54m/F8SEN35+fmoLuaIyTXpD5E7OTnpDVF4dP34cS5cuxYIFC9QWqggqZklq5gbMGz4co4w2eh42n1L7iIiIiIiIyCluDYxVqlRBp06d5CKforVp0wZdunRx2G/QoIE8pzC5e6PxfGQskr27Y2JMDKK1tvSffvhu9SYwMxIRERERETnPrYFRLNgsAmPv3r1lMwKio76Yrlec41gm4r6Kwzl4I3zkCISprV4dRuH1qZ2QMFeMOE5CzAG1Qzt+o9gmRyDVazEiOWkVjENkAJUjlaMxf5MeOTM3zFWjlxbXyt2LlZH6+WPnmcOp+VjraxAREREREZV1bg2M165dw8mTJ5GcnCxbXl4eTp06ZdV3SeZuJCRpP73vQ6iRFk18cH9oK+1nFuIPqJSnjve4OxT31k9B+jl9M7L2a8eIF7lIjD+kBVAhH2npmXJbivlA07VyE+NxWOzW5J9J16KoHhZnHrwPr8qRzgUY1CofiZ+tZnksERERERGVC2XuGcaaNWvC09NTtqpVXbu93JR0Fe7s8+nWG118RB48IEcQM3fHIxkeuCu0HQLz0iDyoMc9HXCvjwqCuYlIOHQJwX0fRpB+CU0e0tPkgWjfzkddSw+Wua37oofIpIpPv2mImtoHgbLnCf8A7c3zz8j3ISIiIiIiKuvcGhirVauGpk2bIigoSDYREn19feU20UR4dIVXM380VK/t8gpGSFuZGLVAmImf4uXwIkLa6ZFO8GjWCeHaMSII/ihHDT3g799A7stPO2N+DtKjGTp2b4uG4lq7RLDMhEeAP+SR+WlIEwdalKmOGj4Wy+OYFImochGVJGI2bFdaSkqKOpuIiIjcrWKVpHoGwF/Lg+aSUlteCA7VQh6ysDt2IbYZ5ahaXtRHJz0Q4N9UPyZrF9avO4Rzory1k35dWWqaq5euejTyR2BwKNr4aNf6cp0WLL0RGtbJYhQxExsXL8HOS60xeI4oSY3CuHBxc0RElcfFixflEkqutNWrV6uziYiIyN3KXEnqLfHqgEdlTWgW4laaJ64Ry2wsVBPReHUYgO7aIfmpqXJynAci9JLRvLQ0UzmrlwyC+Tidmgnv+8IQ5tUM/sbQpSpdldSIpbyWfG7SC81MB9qQ5a0cYSQiIiIiovKjzJWkBgYGWvVdJZ4bXDoxHA2ztmGJMTvp9INoM8x4ltCY/EZTYHIcD/g30o4yBUQxamhxgCg1PaO/9AhopF3PHBBlsJSvhHykn8lH338ORlD+EcRO1+5h7L9xqlm7wktmiYgqIPF3fYsWLWS755574Ofn57DfrFkzdVYhzn6JN8Tf7ZM/QILaBOTg5/emaH/n/wtvb05V24iIiOhWVcnOzra7TsWOs78g40q2fD00qAc8q7v2PKEzVqxYIZfKEE0Q5agNGzY0BUXb/s8//4yhQ4eiefPmsl9cYqmMV5bE4Xr3yVg4osB0qkRlwq7UQ0jMOiFfd/W7F74168nXVNCYMWMwe/ZsGTzIdWeyM/Hq+nfx4Zg31ZaSc/78efl3/fTp02X/8uXL2LVrF3r27Gm3b3u8XSIwPr8WvzboiWcX/R0hcqMIjLMQtfMy2jwxA89FNJFbicqSq9euIeLt0fh07CK1hahiOX78OJYuXYoFCxaoLVQRuHWEsWPHjqawKAQEBMDDw0P1CvZtjy8eY6kM8bwinykkIiptN27cwLlz52TLysoq0K9SpYo6soTl7EH0FFVpYjUiaYxGTsZ/4+WGgqOWRl9rkR8YBxnnadv/NR9fiYFM4z0KXNtipNP2Puy9r2WzHDl14TPk7HkPz2nHjJ2/GanOfEa5aY752oWOzp7F+jnGceI7+dH8XVg19X42n0u/J+trmJr4LpNtv0dL6jzjO9dYf1YiIipNbg2Mlov2i9avXz9EREQ47IvWoIE+Y2mxGc8S2syOSkREpeP69eumycyOHTuGq1evWvVLhQhasz5C9eFi0rEYLB7fBQ3Of4sYU/izII6dtxa/qq6QY7FM04X98XqIydH++3FYbc07g7POPJYu72MZvrvcFkPmint5C/8XdB7bFloEOU39nlMK3qcrn6Eodj6jCItT155EmyfmatdfhrFdauHw/962ui+dCGzP4/8lN0D3Kfpn6H7yYxzptFCdJx62MPYtwlONtLA48wjay88bg3mDgpB/6DP8b/NV9J9ufAfaKZ7qO/n/XkDvRvKNnKOF0WXLduK86hIRUemqWJPeOMOrA0Yu0P4D9e5URDAvEhGVuurVq6Nz586y3XfffXLJJMv+zZt2n4womhae3jGNVI1H1E6LlXjrdMKohVp4CVVdtexSXtoZmxGpHPz88f/wncWpQl5auhZIPHFPh3u1kLYf8SK/iaWWtOAX8bB5Zd6iyHO0a9d/sDd6yypZP4T30oKfdvUD4qJ2eaKRn48Ln6Eo9j7jWfyUkKy91T1o107cWB20Cm1j/77O7sZB7VCPtr3RQ96Lnxb8zPdVgN+jeEmEQFUV7CmXnMrDGacSdlG08Pof6+BLRESlq/IFRiIiuq1KrSRVPMMYo49imUe6zKzKLcUzj2q7pfzEj7FGPPfY92G0VNvMPNHs/m5o01CEqB+RFH8Y58XyTd5iXx7Sz1jENlN4tQ6uevAs2oVvF8r7nCRGzho8iF7qGcyiP4MYrdT3y3PVVkt2P2NOCs6K28w7hI+nFX6+5Wirc4xy2MKva5fVLwEKlshmb/2PHOns3FeEbiIiuh0YGImIqFS5oyRVPOM2f22yqdQz+q1BdgLheezauBOX2z6OJ7rLFKjk4IRYcNezEfyaBiOkTUNc+OELfHb4HOrfF4r29kbMTOHVOrjqo2tFs7pPLTT9f/M341enPoNRCqpKVtVWMwefsU4z+InbNMpC5b3rbcHfrYcOjZFNZ539comafEiUujq6LweM73HZeDzUMA+HP/vQ9NyiCLebvxHfxwgMvUdtIyKiUsfASEREparUSlJdcHZ3gv0yRi0wPfa3CFjPqZqHNBEYJVWqmZeK0+caICw01KUAVUes66sdfOGHr1TwOYu4LTtxXnvfXj0d1XTa5/AzFMXuZ/TD/SFB2kf9HQcPFlHg6vcA2mmH5v+egF/koWIE8VU7zzrak6OPzKreLdMC5XCbQEtERKWLgZGIiEqVGFE8evSobGLKdbF0hqN+SkqKOuvW1Ok0BEO7NDSVek7dWgftCzx62ADdx5iftSvAMwCNtH2mgNjgPmh50cSpZwnFc4hTB6GlqfTzefy/k20xZIb1+xr3KctOtVD0rxci0NKpz1AUx5/R79GJaqKbafp7y2Y9GY/OD/0njsdDtYzPMB7/q/GYw2cY/R59Bv8XlKeuOx7Rp+9CW2cTtlGSOn4ZvtMCutW9i9HQ54xlVIiI6HZx6zqMROQY12F0HtdhvDWluQ5jTk4OVq9erXqQo4kiQNaoUcNuX6hTpw6GDRumekQVB9dhpIqO6zBWTAyMRGUUA6PzGBhvTWkGRiIyY2Ckio6BsWJiSSoRERERERHZxcBIREREREREdjEwEhERERERkV1uDYzffvst1qxZ41I7e/asOpuIiIiIiIhKk1sDY1JSEvbs2eNSu3jxojq7rMnF3uhI89Tkk1bhgNpDRERERERUHlXMktTMDZhnWlNKa6PnYfMpta8UZG6Yq73PWCyPy1RbStht/jxERERERESCWwNjlSpV0LNnTwwdOlS2jh07on///g77Ysp8cU5hcvdG4/nIWCR7d8fEmBhEa23pP/3w3epNKJWMlbsXX25NAizeT7bFIxCmDrklIixqn+dE66F41bj2u1MREaj2ExERERERlRK3BkaxYHOrVq3QqVMn2e666y6EhIQ47IvFnMU5jmUi7qs4nIM3wkeaA5tXh1F4fYIfvo60GKUzmiod1UcJzdvHzrMMmDblprJNQox2Ym5iPA5neiD4wTuw2WafQYZYi3OnrFI7tbC5UtyTqXw1ExvnWp6vve8XW5Hs0RoDhvUBMyIREREREd1Obg2M165dw9GjRxEfHy/bpUuXCvRdkrkbCUnaT+/7EGo7vOfVASMXxCA6aiK6+Gh9Y0Rw8QgEamHxhdgkbdNkfURyYji8jqzBXFNozEN6WiagBbfBcxZgUCu5UcpLS9MCaj4St6YibI5x/SzErdDLRkVYfGVJHK6ra88f3ApZ21Zg/iYnxjtzE5FwSJS5XsR3i8yB0zrMEhERERERlQ63l6SKUcMGDRrIVr16ddStW9eq74rclHQtvLkqEz/FaylTC4O9HtZTpleHAeiuhcL8Y/H4xTKZeQQgwO4wnweCHx+ml4l6BSOkrZZI888gPTMXifGH5IhnaJh+bZ8HQhGkBczj8QddCH118dBkUY4ahXHhPsg/8hk+ciZwEhERERER3QK3BsY77rhDPpfYtGlT2WrWrAlfX1+rviu8mvmjoXrttNwUpBeVMtUxHo38IQYnnZOP9DO/6yOTyEKcMUIonq/UDygGLwSHttU+Yz7S0ktpgh0iIiIiIie9+eabGDhwoGyRkZE4fvy4qS/aTz/9pI6k8qpilaR6BsBfJLqs/Yi3eIawUF7N4F9EyjSeU7wrtF2B5wg9AwIcBDgP+De6B/4Bsv4V4XKE0NyipvKZRCIiIiIq/5o3b47u3bsXaA0bujyUQ2VQhSpJFc8pPtpDPGCYhbiVFusgZm7AQofP/fng/lBRf3oEW77Rz8jd+wW2iYlPO0cgIlCVlXrcjZB2BSOeV3Ao2miZMGv/Af39Mrfj67hMeLSOQM8wY0QwSwuwziZYC6by1mNIOCju3jypj1HiSkRERETkTvXr18fIkSMxYcIEU/vTn/6EvLw8dQSVZxWqJFXw6TdNTlrTMGsblqhJYkZNP4g2hcwy6tNvknw2MGvbInn8BDVJzcIRLbE3eiaWx11D+BgHS1mIyXReGowg4/3UEhjT1AiimKH1RTnRjX5tvY22nvTGdK+RWCsm7ZElrOKYC+gw6iUMapWPxDXT1X4xWrkYw5kXiYiIiKgM+Pnnn7F9+3bVA65cuSL7ly9fVluoPKuSnZ1td52KHWd/QcaVbPl6aFAPeFZ3PbwVZcWKFahWrZocZRQyMjLkCKMRFG37iYmJeOqpp+Swd0Umlvh4ITYFwUNn4IU+LFytrHalHkJi1gn5uqvfvfCtWU++poLGjBmD2bNny19AkevOZGfi1fXv4sMxb6otRFQarl67hoi3R+PTsYvUFqLyTzzDKJ5TvOeeezBp0iQ56PPVV1/h3XfflftffPFF3H///fI1lU9uHWEUtc1hYWEyAIomhq7btGnjsN+vXz/+g5CIiIiIqIz5/fffsWHDBly/fh2bNm1SW6kicGtgDA4ONi3K72wzRiOJiIiIiKjs+PbbbxEdHY0TJ/QKKaoY3BoYyT7xHGZ0zLssRyUiIiKicoOjixUTAyMRERERERWLeEZx3bp1si1YsAB33XWXqS8an18s/xgYiYiIiIiIyC4GRiIiIiIiIrKLgZGIyp20tDRs27bN1PLz8/Hjjz+a+keOHFFHEhEREdGtYGAkonJHBMJly5aZ2sWLFxETE2Pqi1naiIiIiOjWuXXhfiJyjAv3OyZGET/44ANMmTIFd9xxh9qqE4sFV69eHePHj1dbqChi4f6/RD2rekRUmhrV8+XC/VRhHT9+HEuXLpWT31DFwcBIVEYxMDomAqMYSXz66afRt29ftRWIj4/HkiVLEBYWxsBIRER0mzEwVkwsSSWicmv79u04deqU6gFxcXG4cOGC6hERERHRrWJgJKJy67fffjMtEHz06FEZIImIiIio5Li1JFVMTJGRkaF6zunRowf8/PxUj6jiYkmqY0ZJqiCeYXznnXcQFRVlmh21e/fuLEklIiK6zViSWjG5dYQxKSkJe/bscamJ2RDLplzsjY7EqOHD9TZpFQ6oPURUeq5fv45XXnmFS2kQERERlQK3jjCKEQFRRuaKMWPGoEWLFqrnQOYGzIuMRbLqwqM1Bs+YiohA1S9hmRvm4oXYJNVTvLtj4uIRCFPdYsndi5Uzl2BnpuqbeCB46Ay80KeUPhCVCRxhdEyEw61bt6qe9l3t2iUnuvH09JT9Vq1a4eGHH5avydqvZ1OQk39Z9YjIWUH+zVC7Zi3VIyJ7OMJYMbk1MK5YsQJt27ZFkyZNZP/QoUNo2rQp6tata7f/+eef47HHHkPz5s1l357cvdF4ZUkczlkENrHtja8b4V9T+6DEI5YR6q6VQEAsUiY2zo3E2iRvhE9ejOGl+2bkZgyMzhO/SJo9ezbL1Z0w9sM58KnbAL61vdUWIirK1sSfMKPfP9H+ztZqCxHZw8BYMbl9hLF3796mAChGCYKCgtCwYUO7fXF8r169ChlhLCRQORqtU8Ey0GaU0KP1UEwzBUxRbjoTy+MsT9bfY9B1EVB3w7fvQ7ix8Rs1qmn9/qYQq3e1t5yMhSO0nQXCZuGB0LhOrtW9UUXFwOg8BkbnicC47O/T4e2l/yKOiIo25/N38efmYQyMREVgYKyY3PoM49WrV+UoogiGoonnE237LsncjQSR+bzvQ6jt6JtXB4xcEIPoqIno4qP1RVCM0foWYVEEuWht29KJ4fA6sgZz522CPmF/HtLTtLAoSlvnLMCgVnKjlJeWpgXBfCRuTUXYHOP6WYhbMQ+btZONkHddXXv+4FbI2rYC8zeZlwJwTibivhKh0xsPRDAsEhERERFR6XNrYBSzG4qSUzGKKJp4/igwMNCq74rclHTTKJ7zMvFTvJYytTDY62E9ZXp1GIDuWijMPxaPXyxznUcAAuwmNQ8EPz5Mf0bSKxghbbVEmn8G6Zm5SIw/JENeaJh+bZ8HQhGkBczj8QdVGHVSYWGYiIiIiIioFLg1MFatWlU+nyhKTkWrXr066tWrZ9V3hVczf+jFqy7ITUF6USlTHePRyB9icNI5+Ug/87s+MoksxC1Ss6daTsbjtFzs/WKrdp4WTCMeLuXnJImIiIiIiHQVqyTVMwD+ItFl7Ue8s2taeDWDfxEpMzcxHoczPXBXaLsCpaCeAQFaSM1HWrrtw5Ee8G90D/wDZP0rwifHyJJUo0W58gxi5nZ8LZ6f9LgbIe1YjEpERERERLdHhSpJFc8pPtpDPGCYhbiVFusgZm7AQtPziLZ8cH+oqD89gi3f6Gfk7v0C25K0mNc5AhGBqqzUQVjzCg5FGy0TZu0/oL+fCncerSPQM8wLwaFttUCZpQXY4q/KmLk7Xo5K6vejbyMiIiIiIiptFaokVfDpN01OWtMwaxuWGIvoTz+INsMcj+j59JuEceE+yNq2SB4/QU1Ss3BESzU76jWEj3GwjqOYTOelwQgy3i8yFicsZjH16jAKL8qJbvRr62209aQ3pnsVM6TKDYhbpI7J3Ysvt8qHF03PQRIREREREd0Obl+HMS8vzzSSmJOTI19Xq1bNbj81NRUjR44sdB3GiiBTztqawsX5Kzkuq+E8LqvhPC6rQeS6OVxWg8gpXFajYnJrYBQBMD8/X/Wc07hxY9dLVcsZBkYSGBidx8DovMICY2JiovxFnSuCg4NRp04d1SOqmBgYiZzDwFgxubUktUmTJnK00JVW0cMiEZG7bN26FWvWrHGppaenq7OJiIioInJrYCT7xHOY0THvcnSRiIiIiIjcioGRiIikKlWqyBLTTp06yXbPPfcgJCTEYV+UoopzipT5Gf750gC0sW1z/4N96hAiIiIqmxgYiYhIunnzJnr06IGhQ4fK1r59e/Tv399hXzwzKs5xVp27R2PLG1/gcOQoPKS2ERERUdnGwEhERNKNGzdw9uxZnDx5UrYrV64gIyPDYf/q1avqzMLlnDoNMX1TvQaNHS5vZDsK+cC/N+AU0hEbZTEiabRZr+Cz047OISIiopLEwEhERJIYLRSzpJ4/f142EQgvXrzosH/t2jV1ZuEuZ6TKwOiQCH5LD6DvhC9w+I0vsK1HO+Qc+y/e3HYVg8eKbf/BK02142q0x1xxzOxX8HgNR+cwMhIREZUkBkYiIpLuuOMOORt1aGiobLVr1y6079ys1Tk4dv6s9rMWWjX01TfZ8nkc/xYhsLHereXbBHfiMpLOZegb7CnOOUREROQyBkYiIpJKpyT1Mk6cSwdqBKNnK0cFqTn48eNnzKWlH28ufERSKs45RERE5CoGRiIikkqlJDVzF745qf2s2QR3qtFAW+lfz8OoAzno2StKlpfuHhKBO9U+R4pzDhEREbmOgZGIiKSSL0nNwY/fbsB3qIWenfugvdpauBwcStrv4mhhcc4hIiIiZzAwEhGRJNZUTEpKwp49e2Q7fvw4EhISHPbFaKTjdRhFyegUjDqQrr2+jG+3jDWVj7ZZEK2FSHHIlxg26xXsajsRrzQ1jvkbJp1tiV71xAGO+T/i+jlERETkuirZ2dl2F9HacfYXZFzJlq+HBvWAZ/Wa8nVJ+vzzz3H6tJgb3XkDBgxAkyZNVI+o4tqVegiJWfqYSVe/e+Fbk/8admTMmDGYPXu2XBeQCjf2wzlY9vfp8Paqq7aYffvtt/IZRcP169dRtWpVUyi07Qti3Ub737sKjIebYO5o8+Q0ZkXtJyo75nz+Lv7cPAzt72ytthCRPeIXi0uXLsWCBQvUFqoI3BoYo6KicPToUdVzjviHYYsWLVSvLMnF3uiZWB6XqXe9u2Pi4hEI03tELmNgdB4Do/MKC4wli4GRKg4GRiKqzCpmSWrmBswbPhyjjDZ6HjaX4tJcmRvmau8z1hwWS1LuXqyMtPgsw0dj/iauM0ZERERERKXPrSOMK1asQNu2bU0lpocOHULTpk1Rt67+m2/bvihhfeyxx+SkC47k7o3GK0vicM5ihE9se+PrRvjX1D5wNKl7sYlAN3MJdl4rjRHFTGycG4m1Ka0xeMZURASqfpI3wicvxnAOX1ZoHGF0HkcYnXf7RhiJKg6OMBJRZebWEUYxhbsIiyIAiubr64s777zTYd/Dw0Oe41gm4r7SwiK0QDXSHN68OozC6xP88LXVSJ1qk1bhgHaMPkpo3j523iaYx/FEuWmk1f5RwychRjsxNzEehzM9EPzgHdhss88gAuvzFudOWaV2GqOH6h70gGhxfm4K0s/JHYon/AN81GsiIiIiIqLS5dbAKNb0EqOIu3btkk2s72Xbd0nmbiQkaT+970Oo7eibVweMXBCD6KiJ6CIylxiBjNH6i0cgUAuLL8QmaZsmI1rbtnRiOLyOrMFcU2jMQ3paJuDRGoPnLMCgVnKjlJeWpgXUfCRuTUXYHOP6WYhboZfBGiOe19W15w9uhaxtK5wrK/UKRkhb7WbzjyD2tXmI/e9iWfbq0ToCPTm6SERERERlydFYPDflf0gubHyHyh23BsZq1arJkUPLNb7EhDaWfVfkpqRr4c1VmfgpXkuZWhjs9bCewrw6DEB3LRTmH4vHL5a5ziMAAXZrWj0Q/PgwRIh9ppB3BumZuUiMPyRHPEPD9Gv7PBCKIC1gHo8/aDGC6YgXOoxaIEOmCI2bv9Hvc8CwUiitJSIiIiIqDhEUBw3E5J9uIrAKsH/xXzFwMoNjReHWwCimZhdlprVq1ZJNTNdes2ZNq74rvJr5o6F67bQCZZ92qGM8GvnD+YLQfKSf+V0fmUQW4hapktTIWCTrBzhBL1F9ITYFwUPnyJHPhmK0cbp1ySsRERERkds0H4y3167D+Dv24Lvja3Eq7GOsW/QEghwt1UvlSsUqSfUMgL9IdFn7Ee9soPJqBv8iUqbxnOJdoe0KjOx5BgRoITUfaem2M6R6wL/RPeqZQzFJTYwsSTValDMT8KgSW4/Wj+PJPoHyWcwXxWijFkDjDzAxEhEREVEZoEYYl13vhIfuGoTAA0M4wliBuDUw3nHHHXIW1KCgINk8PT0RGBho1XeJVwc82kMPVHErjYlkNJkbsNBqEhtLPrg/VC/53PKNfkbu3i+wTQtq3p0jEBGoyko97kZIu4IRzys4FG20TJi1/4D+fpnb8bXpOUMvBIe21QLlrQW8/DPp0ONoLlLkcKgHAmQyJiIiIiJyMzXCuOj+KjilhcT7Jn3CEcYKxK2BUZSciiUzGjZsKFv16tVRr149q76rfPpN00s3s7ZhiTEz6fSDaFPIc38+/SZhXLgPsrYtksdPUJPULBzRUi3Gfw3hY8SyFuoES2IynZcGI8h4v8hYnGg9FNPUCKIxKmhcW282ayma7lUsmSE3IG6RdsyeUEyw+ixircdLCB46Ay/0KXJ8koiIiIjo9hHBcSGDYkXj9nUY8/LyTCOJOTk58rWYDMdePzU1FSNHjpQT5VRkYokP/blFBsPKjOswOo/rMDqP6zASuY7rMBJRZebWEcYBAwbIhfh79eol28CBA9G3b1+HfREWGzdurM4mIiIiIiKi0uTWwGi5aL+zzeXnGomIiIiIiKhY3BoYyT7xHGZ0zLssRyUiIiIiIrdiYCQiIiIiIiK7GBiJiIiIiIjILgZGIiIqEYmJidizZ49LTcyGTURERGWXW5fVICLHuKyG87ishvNKc1mNqKgoHD16VPWcI/7sWrRooXpEZROX1XCfX9NT8FT0dNUjopIW5N8MH4yao3r2MTASlVEMjM5jYHQeAyOR6xgY3UcExtU/bcSiv72othBRSbl8JR9Prni+yMDIklQiIioRVapUQXBwMDp16iTbXXfdhZCQEIf9OnXqyHOKdHY93hg+HKNs27MxiFeHEBERUelgYCQiohJx8+ZN9OjRA0OHDpWtY8eO6N+/v8O+GBEW5zjLo+0TeC0mBtFv/RUt1TYiIiIqXQyMRBVA3oFoTJm9ASdVn8gdrl+/jrNnz+LkyZOyXblyBRkZGVb94rh0Ih3ntZ+e/o3QRN9UkM0o5Nj5m5GKs9gwx2JE0mij5+OrU47OISIiIksMjETlmAiK4wf+DfOTqsMfl7D9tYH4mxYcz6j9lYlTpY0V1nl8v/QZDBw4CgvjMtS220+MFopQmJeXJ9uNGzcK9IvjcloazqnXdongN+Mw2s+JQXRMDOb9NQj5hz7FR5v/QL/pYttbGBikHefRFkPEMe++gN41HJ0jkiQREREZ3BoYV69ejTlz5rjUUlJS1NlE5Bk2CsvWvYfHcnfjp4QtuNJ/HT6c1Q+N1P7KYNeuXcjNzUWtWrXUlkomZR1eHPgcdt/9f+jWQG1zk2rVqqFp06YICgqSzdPTE4GBgVZ9113CiXQRFz0Q4N9Q32TLrz9eEiEwUO/WCghAQ+QjTZ7nQHHOISIiqoTcOktqxZpRLxd7o2dieVym3vXujomLRyBM7xG5zJlZUsUI4/OvfQvfwRHwSKyBxlVjsfnGKLxtJzQeP35cBquKJDU1Vf7i6aWXXkLr1vZnLzxx4kSFWetPTBrj5eWlejbOf4+lL76Pq8PexJRwX7WxoNKcJXXp0qXyOUUREgXx93uAFsSMexb9du3aoWFDPfiJ/wb06tWriL/TRVnp81h3oi2GzFABT4woPv8Jfq3fA5PeGY5QLVT+/P5MRO2wDnv1e0zBguGh2is71yjyHCIzzpLqPpwllaj0ODtLasUMjJkbMC8yFsmqC4/WGDxjKiLUb5JLWuaGuXghNkn1lBILjJnYODcSa02X90b45MUYziRa4bmyrIYIjtM/98dkLSg2VdtsrVy5EseOHVO9iuOJJ55wGBbF6OP777+Pxo0bqy3l26hRo2RotKsMBMYlS5bIWVL9/f1lXzzPWK9ePdSsqf/3Q/Tbt2/vWmAsEA4Lbmu0fg6mfnICrZ+Ygee1v+gv/fw+Zi/dgRuFBMazRZ5DZMbA6D4MjESlp1wExhUrVuBPf/oTmjVrJvv79u3D3Xffjfr169vti5GEfv36oXnz5rJvT+7eaLyyJA7nLAKb2PbG143wr6l9UOKZMXcvVs5cgp3XSmNEUYXFFBV466v3ulS6AZjKBq7DeGtEWBQhedasWWjSxOFUKRVHGQiMIgD27t3b9He0+DMQpahGQLTtFx0YjVHAXFOwkwoNjN6mkcPCRhitA6O9c4jMGBjdh4GRqPSUi3UYxQQJdevWRYMGDWQTZUve3t4O++L5mMKnYM9E3FdaWBSjcCPN4c2rwyi8PsEPX0dazJJntEmrcEA7RowSWm4fO28TzFMfiHLTSKv9o4ZPQox2Ym5iPA5neiD4wTuw2WafQQTW5y3OnbJK7RRhU9yTugc9IFqcn7kbCUmAx92huFf8O8krGCFtfYD8Y0g4yIkZiArzwQcf4LnnnqscYbGMEBMPJSUlYc+ePbKJMuiEhASHfVEq7HiyIsuS0Xwc+d9009+ho0RYFIdc2IrFo+djf9gzGBhkHDMO0afuQlsHjzsa/Pq7fg4RlS3isYTIyEiX2sKFC9XZROQstwbGP/74Q44ibt26VbYLFy4U6LtEBSx434dQ26E+rw4YuSAG0VET0UXLXLJkVKzntXgEAlVJqXf3yXK2vKUTw+F1ZA3mmkJjHtLTMvXS1jkLMKiV3Cjlydn78pG4NRVhYrY9ef0sxK2YBzHZnjHieV1de/7gVsjatgLzNxUn8HmhmaNJH4ioAPELJ7p9xOjhxYsX5aMGol27dg1nzpxx2BfVJWLx/kIZM5uKv6+t2nKM7Wr8feinZkPVW9SsiYhcGGMxUqj2W0xyU/Q5REREJLg1MNaoUUM+zyIWehZNlJ7a9l2Rm5Je+NTrdmXip3gxjNcavR7WU6ZXhwHoroXC/GPx+MUy13kEIMBuGagHgh8fppeImkYBzyA9MxeJ8YfkiGdomH5tnwdCEaQFzOPxBy1GMB3wDIC/HFA07iMXKZzBj4jKqJ49e5oW5RftqaeewpNPPumwL5pYvJ+IqKzJ2PUWwl8agDYWbegG1+bdKAvsfQ7Run+wXfsXsOFXvL/Qcv9wzPjRvJfIrYGxpHk184fL42+5KSgyg6ljPBr5QwxOOicf6Wd+10cmkYW4RaqUynIynqJ4dcDgJ8PRMP8IYqeL88eaZ2ElIhLkshoDMfCZhdh+PhvfL/mXXI9x+ff8u4KIKj4xqdmCBQtkE8+sP/bYYw77oiS1aBn4OubvCP9iJxo9tAiH3/hCts8evAsJ3022CVrlR4j6LHEDusDqKfdzWzH9tUgsyLgHz4/WP+vh54bjxver8O15dQxVehWrJFWNyCFrP+ItniEslFczFFXlaTyneFdouwKT5nia1u6y/evDA/6N7oF/gKx/Rfhkc+mTLH9ycgIe8fzlW6bzojAuXLuex90IaefM2USVx/79+zFz5kxTy8rKwqJFi0z9Tz/9VB1ZwTQbiDfXrcM6qxaNcX92/tdbZVNtdPzHQpsyUktF7SciKoZjW/DvxCzA7wm83s88yWLQoxMQqSWt9COf4cvj+jar0bvX38a38R/ir6ZROnMzQmbylxMttqtRvGOOz9ktjzdG+/Qga3ueOcDa7FcuZJ7U9tRHy4b2J85L/uEzfHpZBMoJGGlMwt2wB+ZEPoeebl7bl8oOtwbG6tWro02bNnKmVNHE9Ott27a16rvEqwMe7SEeMMxC3EpjIhlN5gYstJrExpIP7g8V9adHsOUb/YzcvV9gW5IW8zpHICJQlZU6CGlewaFoo/27LGv/Af39Mrfj67hMeLSOQM8wLwSHttUCZZYWYJ1NsIVQ19bvS20jIkkExJMnT8pJVEQTz9OJsnfxWuwTkyMQEVHFkpeXh/Xr18u2Y8cO+Rx1YX0xWFGY5F9245D2MyTofljP3+yNOxuK5+Iv4Pe0TBkWB32xE1VbT8EOMXLX8yZWxDfBCjFC988haKsd6a/2bft7N5zXwt/oC/8n+4ffWKCFzwtY980qfFvvb/jEwTlWD2adO4jtJ0SQjcDwPxX8hWDyl69hkgi6VjKQct52m6VfsfNXkX7vQe+2jlcgIHJrYBT/kPPw8ECtWrVkq1q1qlyvy7LvKp9+0+SkNQ2ztmGJMaPe9INoM8zxiJ5Pv0ly5C5r2yJ5/AQ1Sc3CES3VYvzXED7GwTIWYjKdlwYjyHi/yFicaD0U09QIohghfFFOdKNfW2+jrSe9Md2rsd6iKGEVxxxUs6aqpl37rLwv2xl9iEioXbs2hg0bhldffdXUpk6dWmHWYSQiImuenp7o37+/bF27dpWz7xfWF79IvDUX8Ou54ziQfFCLY/fg7127yceVfDs/j7VayHNU2xH06BIZAvX9KnzmnsKJi3JDkTKS9+I7MRJYIMhqjn2I6T+oYU8rWThxTgTG+rhHVrzZOHcSv+eq10SFcHtg/O9//4s5c+bI9tVXX8l1uRz1U1JS5DlFsS7j1Nq7FmHPmC3Vas1EL3QYtcB8vNb0UGZst1wo3wd9p4ljLLb59MNUi3Nty01FiLW8dnTMu3ihj3aEcS9W+/SZVHX11XuZG8MikWOnT59GXFyc6ulEXyzhQEREdOtEeedNFcRcIJ8VNEpO/2FnNNCRC1j3+SiEf/ELuj4WjTUWZbK6U1j56cc45NcXk4NtZgY3AqHfA+hilJtaatgU93ip10SFcGtgFCMBEydOxJgxY2QTr8eNG+ew/+KLL5oW+ScisscyINoLkEREVHGUdElqfZ+mclKYhOSf8Ju+SbEcrbtLlac661e8H/MOPq3SFUufFyWp72OxbbhzqD4GakExbsC92KEFR9uZWtOPxGKlmLDmLwNhmwmNUUn/ho1g/92MMtvf8dWh8jcDLN0+bg2MYv0tY1F+Z5tYvJ+IyJHLly/LiV+E+Ph4JCc7PS8xEVExncf3S5+RMxQvjMtQ2+h2KOmSVN/Oj+PvIjGe3YwY0+QxYkKZ17BA+6PVJ4fxRVhQOy1YWgStYx9itLMzqBrPI7rAuK+E/Z8WmL3UasIak1/xxa6dVmWzBfnika695bOTCd8txUpTVasWcFe8zVlSycStgZHs00tYVdkqEblMhMRNmzbho48+UluIiEqJXNrmOey++//QjbNKVgAt8Y8pYgTwpiwFNZeQVpEjfUZJqHhm8T9qqQ15zIdnMLi/o2CmXfMvQ9A2dwcmvKUd+3YMzjcNsV7eokgt0aWllgq1a/xnl3k0UEySs6xAmeoxvL9QLJUhXv+Ot941SmEHyOVCxOb0IwvRddH/8Nvdf8Mnzz2Lv9SyPO51HL9vBGdJJZMq2dnZN9VrKzvO/oKMK9ny9dCgHvCsXlO+JqLbY1fqISRmnZCvu/rdC9+aLs4aXMls27YNy5YtU72CunfvjvHjx6te5TX2wzlY9vfp8Paqq7YQUVHmfP4u/tw8DO3vbK222HH+eyx98X1cHfYmpoTbjwLHjx9Hbu7tm2VETB7YunUh91wO/JqegtU/bcSiv72otpiJ2a8XLlyoes5p0qQJpkyZonoVlViIXwuMVZ7AF5OfKDhJTpH7qbK4fCUfT654Hh+MmqO22MfASFRGMTC6RqzbKp5ZNIh/RIwcORL16+sTk3t7e8t/KFR2DIxEriupwLhy5UocO3ZM9UpfWloaOnfuLP8uLK8KC4zkCAMjOYeBkaicY2C8NWKirNmzZ8PPz09tIaE0A2NxRk/uuusueHlxmj4q20oqMN5u4hdps2bNwn333VduQyMDY3EwMJJznA2MfIaRqALIOxCNKbM34KTqE7mDCIyHDx92qd3O8rxbcSXle6xbuRpbDl1QW8idchI2IoZ/HkUSFRbiF2dihlCqTMRzmF/gsMMwWNR+ImsMjETlmAiK4wf+DfOTqsMfl7D9tYH4mxYcz6j9lZ0z67ZSOZCTgE0rV2oBwabF7sIpdUjpykHyoWRcqu6LJo3ri/SI7z/R3n/1V7DKK8Z93rb7qrzq3B0IP1xF5qnTcHE1vErHKMsnIiouBkaicswzbBSWrXsPj+Xuxk8JW3Cl/zp8OKsfGqn9ldWuXbvkyFWtWrXUFrodREAXJaZt2rSRrXHjxmjZsqXDvihFdSXUV298Px4bORLDB3XQwsJtlHMMp9K19/cNRBOH//bOwcGde3FW9aiU1bkbgf7A1YxTSOUgIxFRqeIzjERllDPPMIoRxudf+xa+gyPgkVgDjavGYvONUXjbTmi83bPzuYuYNW/16tV46aWXyv3sgKWhNJ9h3L59O9q2bQtfX/35rd9//x3+/v6mZxRt++J4ERyLes5UlIOu35qMG8GP4K+dA/WRvLVaOPMKRs/BnSEXIDK2yTP0cNm39504uXEt9mlhz0r1xujYrzfaVrN3TtsCC1wXeH8xwvjFVvx2RV2n/hWkfP8Ftidf0k9Q9+Vb5Hny4vo2dapk3J+9/RafWZRl/r+959Ho/n7o1baWuocrql9f7Vcf3vK7MrG4b8v3tPguaxn3bnms5IVWjwzGn4wLWn3/5n1W9yBVV/dXDQfFn8152+/QfP+Fv6ex76b1fZSSQp9hFMtqTPnIZpH3eugxZT7G/dn+Igu328CBA03r05Y3fIaRqPRw0huics6VSW9EcJz+uT8ma0Gxqdpm63bPzudOTzzxBMOiA6UZGLdu3YrAwEDUq6f/b1VMuFG7dm1Ur17d1G/atKnLgdEIHabwYhsYRf/zM7hTBR7rICUTkE04kRct4hyzAvtsgl+Li3owvFK/Pmpqn/GSK4FRfZYLlgHXuM9a6vibFp/TdGxb3GF5Xy0uWh1bz+Y7E59hc26ICn8G9b3IPGcEOeugqYfoFsi2Cmc236cRvC3/PDblotUDN7Df4vNbf49FBUY9AP9UtbP1d2d8F9q9FfZnVtKcmvSmDGNgJCJ7GBiJyjnOkkqloTQDo1gLs1mzZqZnpjIyMlC3bl3UrKn/90P0xdImrgVGOyNPKjhZjTBaKDAiaC8w2ih4jsHOSJZl8HskGFk7VJDp44WDFvflTGC0ft96VvdpBFFHn+POk+bAFF77sMPrOMxSphDWDHfWTsGZO8yhNbFOOzROO4iUutq2brVxqJCw1vn6LrvBzQielqHV+cBoe9MF/wwd/5mVPAZG92FgJCo95WKW1KioKERGRrrUfvvNuuiDiIjKBvE8Yp06dWRgFK1atWoF+q77AxezRcmkmnDGLhE2PjFNhrNGCxFGEaNjxTnH1lWcjf8Jv13yQqsHCwZXw+XEr/X3+UgLXTZv8kd2tva+1VGvbsGlRfR9Fuev1AKTbXmtdg9nfvpMu/9jqHP/43pwunIeF12oPq9ezx9Bgf7684CnxPOa2v3U0Z//vZp9EZf+yMZFcSO5ifhWfV/mMtM/cD7H/pvVCemL/+vgb7p/8zlOEr8YUO9n/7MTEdHtwElvSkwu9kZHYtTw4XqbtAoH1B4iosrgxo0bsuw0PT1dtj/++KNA32VqwhnUqIt6DvJiTsK3amTqcQwfORJDewShttrnSHHOKeBqBk6kXkKt4AcLfYZOjLCJ9xj+ZA+0sHqTK3rYchCGa9SrJ+/JdL7RhlmOGopS0se1+78bOVpw/GTXKaBmA9jJnwWpIFi9bj00EbOOap/nt5+TcFbcT7Om+jX+uIjsy/VQV9yIGDm1vI+Rw9CrrT8a1HHwZldSkJCk/eGJ5yMfHynDo9PE6OdmNVor32sQ2rtwOhERlZyKGRgzN2CeEdxEGz0Pm0txjvPMDXO19xmL5XGZaktJy8TGufpnmbLKOobm7o3G8xaf1XY/EVH5dQUpCVqAEaGobbDDETxrV5B26rSLo4WFnVNTBSIx0mlnOk4t0HQubjlkThIOJ19yOPtqzYBABGhB7fLJk0Uu01GzWQiCtEB1+eghHLpQB3fpU4gi9bR+z6J8c4MIkxaunM/BZfVan3X0KrIuGPdTA3XrqXRbIwCBjbXXudp92LmRAktciLC3fhd+TzuFNBFIC51d1knGLw4sFDY6S0REJcftgXHs2LFYsGCBbIMGDcK0adMc9ps3b67OckwGqMhYJHt3x8SYGERrbek//fDd6k2lsy5W7l58uTUJsHg/2RaPQJg65JbI8BuJtdpb2BKf9ZUlcbjefbJ8z/mDWyFr2yKGRiJyi6pVq8rSUzETqmg1atQo0Hee8UybiHF62aVemqg18ZygOESUSK7+CieadkF7Lezox3yE7y80hMg3hakT4vw5+kjfVWTb1nmKkbNHHJeiFipXPYepvbx6+id8bll2efU0fv4sFj9mNMOfIzrAz6IUVLSPvjpkZ+1BIySexuHEU9rn64luQTVN39ua3VURajfYGoHLCIjV4RPY2DxT7NVs5OTWRLM/R2jfVy6Svjbfh2kdyjoh6NEjCDWNz/HRbtwRdi9yxdqVttezJT+ruN5HVn/Wn+y7Ax3vD0Jt47OvTYRHM8shRjU6K+/7VtMoEREVxq2T3ohnGHv37m0KgmLttKCgIDRs2NBuXxzfq1cvtGjRQvYLEiNxIlx5I3zyYgy3TGxasFs5cwl22g4CiqCnhbvADXPxQqw5lXm0HoppU/uofwiIctOZNiOI+nsMui5C22749n0INzZ+g2SLfcb7G8HunN7V3nIyFo7Qdhr3dE2/hzA79y9GL1/Y0hjDe51GjHZ/pnNN93TN/F4iXBphuaQCK7kNJ72h0lCak97ExcXJtS+N9S+zsrLkBDfGLKm2/ZSUFHTq1Mm0DIc1FRiP1XUwcUtR+0uQzeykDsOPK9Q1L9mZsEWfHObSbVkuoqxxfiKboicyKkmc9MZ9OOkNUekpF5PeXLlyRYbC9evXy3bu3LkCfZdk7kaCyHze9yHUNi15dcDIBTGIjpqILmJZJGNE0CIsijAmRyQnhsPryBrMnWeMSuYhPU0Lix6tMXjOAgxqJTdKeWlpWhDMR+LWVITNMa6fhbgVehms/VHAFZi/ybnxTp9+0+Q9tlV9M+OeGsHfWObJM8D8mojoNhMzpBphURAzpBrhULDt2x5fZnGR+LJHlaiWSLkrEREVyq2BUUy13rlzZ/Tv3182MZJo23dFbkq6aRTPeZn4KV5LmVoY7PWwnjK9OgxAdy0U5h+Lxy+Wuc4jAAF2f+HpgeDHhyFC7PMKRkhbLbXln0F6Zi4S4w9p9+StBVj92j4PhCJIC5jH4w+WToksEZGb3HXXXXLhfqO1a9eu0L5oxhIbZVsdBLUNQm1V7knul3PsFM7CC/do/xsqkRFfIiJyqEJNeuPVzB+uRUxNbgrSi0qZ6hiPRv5wfgAvH+lnftdHAZGFuEVqYhpRMqofQEREDonn5v5qMyOopaL2l6yazf6MgSNHltx6f3VC0MfB9cRyFMNHVr5yVMHZ77kyf0dERLdbxSpJNUoys/Yj3tl5X7yawb+IlJmbGI/DmR64K7RdgckNPAMCtJCaj7R024cjPeDf6B74B4gbEs8kqslwVIsyPR9ZXJ76teVIptqUlyZfuxZsiYiIiCofsRTQ+fPnXWriWWyiyqZClaSK5xQf7SEeMMxC3EqLdRAzN2Ch6XlEWz64P1TUnx7Blm/0M3L3foFtYuLTzhGICFRlpR53I6RdwYjnFRyKNlo6y9p/QH+/zO34Oi4THq0j0DPMC8GhbbVAmaUF2JKeubTgtTN3xyNZC6r2gi0RERERmZ05cwZz5sxxqUVHR6uziSqPClWSKohJYsSkNQ2ztmGJsT7h9INoM8zxiJ5Pv0kYF+4jl6QQx09Qk9QsHNHSPBPpmKn6M4q2xGQ6Lw1GkPF+kbE4YTHDqleHUXhRLXdhrJU4avho60lvTPdqLJ8hSlj1Y/Q1HoebZnDVr6Pvs732C7EpCB46Ay/0YVwkIiIiIqJb5/ZlNY4ePap6zhkzZkwhy2pUDHIpDYa/So/LalBpKM1lNYgqKi6r4T6luayGKDF944034O2tT5108+ZNXL161bRmrG1flLCK9WanT58u+4X5LXYa5m5IVT2zwEdn4dVB96gekXs5u6yGWwMj2cfASAIDI5UGBkYi1zEwuk9pBsbU1FR8/PHHmDJliuxfvHgRBw4cQNeuXe32T58+jTVr1piOL4weGHPQ8elZGNvFxxQgGRipLCkX6zASEREREbmLGEW8fPmybNeuXcMff/xh1RfNdRk4nX5R+1kPfk0cT0MoQqT5caUJiNqZKTZihmmbuT27bKdcOs7uOUSljIGxDJKL9ce8y9FFclregWhMmb0BJ1WfiIiIipaXl4cff/xRtn379skZ/C37xZON9DM56rV9IvgtO9sHb8nZ82egT5OL+Dl2DXZ6D8ZrYtuMfmiiHVe309PymHfGd8EFR+cwM1IpY2AkKsdEUBw/8G+Yn1Qd/riE7a8NxN+04HhG7SciIiLHatWqhR49esh2//33o06dOlb9atWqqSNdkJEKOcBYNwD+Dqr/WwyeK0Ogvh5APfg3qgNcTNPPc6A45xCVBAZGonLMM2wUlq17D4/l7sZPCVtwpf86fDirHxqp/URERORYqZSkZqcjPUfLi630pdfsyojDsvFGaelzWPVz4SOSUnHOISoBnPSGqIxyZtIbMcL4/GvfwndwBDwSa6Bx1VhsvjEKb9sJjcePH0dubq7qVUzBwcG44447VI/sKc1Jb7799ltkZGSonnPEb/H9/PxUj6hs4qQ37lPak96sXLkSDz74oOyLWVBFSaqnp6epL2ZFFX9PCc5OemNvghvrbTfwybTXsCmnE0bOGo8uPhnYsXS2FgC90XfW65CniGcZX9uAnE5PY4YcVfyt6HOIXMRZUonKOVdmSRXBcfrn/pisBcWmapst8R/FY8eOqV7Fk5OTgyZNmmDy5MkMjYUozcBYkZdKuvTz+5i99Cf4PTEDz9tdlLcMOrsebzz/CU62fQLTX4iQz0NR8TAwuk+5myVVjALOjsa+Kkaw0zcXGhhvqnNymjofGO2dQ+QiBkaico7Larjm+vXrWLRokXzN0OhYuQyMKvj8qrom9Xtg0jvDEaq6pecsNsx5HutOtMWQGS+gd6DqJ4t9HmhtGyIv/YzomUvxnZjSEPXRfco7eKr0b9IO2/tWm8llDIzuU9rrMC5fvhzjxo2T/UuXLuHw4cPy2UV7fe3fzPjoo48cr8NohMUiKkXFRDYzIs7gHS0Q6is11kWrDo1weu9ldHEYGM3bHJ5D5CIGRqJyjoHRdSI0Pvfcc3j66afRtm1btZUslWZgXLFiBZo1awZfX1/Z/+233xAQEIDatWvb7W/duhWDBg1C8+bNZd8h25EyI0DersBo+/5GIMxtgsZeqTh9w/o+zq6fg6lf5ur7zrkzMKp7+eREwVBLLmFgdJ/SDIxZWVkyMBrE84zivyPGRDe2faFevXoYP3686tlQgfG3YIuQZ6mo/US3GddhJKJKR4wqiudNvLy81Ba6ncQ/rlq1aoVOnTrJdtdddyEkJMRhX8xGKM4pyqUT6Tiv/fT0b+S4rFKEOtPaZMMxdv5mpMoRNvM2Uxs9H1+dcnROQY7f3xsh9wUBF/YjIV5t0t5zT3wyPJqHItj2X4OFvt8l/Pz+lIL7RDidYj5HtmdjIN5OlMk+r/UjY9SbG9dX+4VaWkBviHykpcvhTiKy4O3tLUcLjfbyyy9j1qxZDvuiOQyLRBUYAyMREZUIMZugKEmNj4+XTZRz2faL43Jamlyw2iERlGYcRvs5Ym2yGMz7axDyD32Kjzb/gX7Txba3MFDLdfBoiyHimHdfQO8ajs4RSdKa/v4eCPAvOB5QLzQULXEBBw4Yoe0nJCR74O6Q1qivb9GJe1SjlGKNtSUTusLr0P+wUIY9ERZnImpHLlo/MUe7n+UY1XCHdi8J2LBYjGSq+14+AQ+5OCRR+05/NNB+5qWfsRuGiYiIisLASEREJUKM7opy1MDAQNlq1qwJHx8fq77rLuGEHB2zH9gkv/54SYRAVXHp1Kia0+cY7++JgEZ2Sjob3I8QOch4AFokxs9fbsWvHs0Rcm+AOkB39qd4/Kp9hrtD7pWjlLWDQ9Fa+zjyvEuJSDikvUf9B9FLlo3WRsd/zMXzD/2BWx4YrBUA8bXln04H1/YmKmW+4Ri/TF9k3+7fVkXtJyqj3BoYxQQJkZGRLjXxDAwREZU9IjDWrVsXDRs2lK169eryeR/LvusuIz1NS00yhDl6Bs+6nHPi0h2Fj0hKxTnHHj90ChWJ8Qds+ewHGfw8mofA+laN0JmPI/+brr/nOGNSHM3lNPvBsHZHjHp1Ah7yOoSPp9ucQ0REdJtwhLHE5GJvdKTpHx+jJq3CAbWHiKgyKJWSVFniqf309EeAg7x4dv1ii3JOvdyzqN/eF+ccR/zuF2WpWhj89EMt0JlHEc1q4045OipmVNXfz9TEZDlqFNCes9u/kiGxfo8pxSpJJSIiulVuDYxVqlSRkx40aNBANjFznngA2VFfzFIlzilS5gbMM4KbaKPnwc5jKSUmc8Nc7X3GYnlcaRX8ZGLjXP2zTFlVMIbq78+QSkTuZft3uhhRFCOOln3XqBJPEbQiejo5G+olJMYfcnG0sLBzjLCXh7QzDv5D4qeXpUoORkKNUHks4ZeCzxLWDkZIW+09LCbPObv+Lby1OUFOoCOW5ggLK+Y0q2r00qOxP9RycERERC5xa2AUs+M99dRTppmnIiIiMHbsWId9MV17UTPq5e6NxvORsUj27o6J6je4S//ph+9Wb0KpZMbcvfhyaxJg8X6yLR6BMHXILZHhNxJrtbcoSA+SL8Ta3UlEdFuJWWr9/PzQtGlT2cQzi+KZRsu+84yJYESMsyjlFM1Yk/HCViwePR/7w57BwCDjmHGIPnUXRP4qjF9/588p+plIVZaqKViOqvj1xwQ10c0M43NoTZ/hVDyzOFW7nwvYtlDf/srhdnjcZw+2y7x4H0IKyYsXti7Ur2fzvYiZYJ2aYZYqnIyMDBw6dMjUBMu+2E9E5Cy3rsMo1r7p1q0b7r77btnfv3+/fC1GFY1+cHCwfPZFEM889urVq5BFnkWAEuHKG+GTF2O4ZWLTgt3KmUuw03YQUAQ9LdwFbphrFbw8Wg/FtKl9oP93X5SbzrQZQdTfY9D1aLyyZDd8+z6EGxu/gVzHWe0z3l+E2FeWxJl+e+3dfTIWjtB2Gvd0Tb+HMDv3L0YPX9jSGMN7nUaMdn+mcwURJiO3oNHIXjizUoXkkgqq5HZch7F4xLPOEyZMkEs4UEGlvQ6jqAQRo4yC+EepGGE0gqJtPzExUf7S0P46jCow/hTgYNH5ovaXIIsZTuU6jGpz2WS9WP99B7gOY0kob+swxsbG4uOPP1a9goYMGYLBgwerXtlWmuswElV25WIdxqtXr+Lw4cP48ccfZdPCq/zNl2XfJZm7kSAyn/d9CLVNTV4dMHJBDKKjJqKLqMsxRgQtwqIIY3JEcmI4vI6swdx5xqhkHtLTtLDo0RqD5yzAoFZyo5Qnp1vPR+LWVISJac/l9bMQt0IvgzXC4nV17fmDWyFr2wrM3+TceKdPv2nyHu0uQe7TD1NjtGB5r+oTEblR9+7dERYWJgOgaH/605/Qpk0bh/1+/frJEckyT5Wc5h9NwC+lUqpSWvQ1IQufMIgqqjvvvFP+8sy2tW5dPkIvEZUdbg2MNWrUQPv27dGjRw/Z6tevX6DvityU9GLMcpeJn+K1lKmFwV4P6ynTq8MAdNdCYf6xeOt/HHgEOJh0wQPBjw+D/OWtl3gWRUuk+WeQnpmrnovx1gKsfm2fB0IRpAXM4/EHS6dElojITURFiLEov7PNGI0s2/wQ3rsrGuYfwpZvjSXxy4Hz+oRB9R/sXbojsFQmnT9/Xo7oi1/kGE30T548qY4gInKO259hzM/Px+XLl2W7ceMGrly5YtV3hVczf9dnuctNKXqdK3WMRyNXJg3IR/qZ3/WRSWQhbpF6ZkU8X6kfQEREDonn+hbqi+zbDTtF7S9ZtTv+A2/FxGDB8GJOPnPb+KHf9Bj9ewnpj5fKxT1TaRCzEm/fvl3OXiyIn6JfrNmKiahSq1glqZ4B8BeJLms/4p2dLtSrmcPpzA25ifE4nOmBu0LbqWcazTxNkyHYPhzpAf9G98A/QNa/Inyy9h9wUQKrWpTp+UgiIiKikvf999/Lf08Jv/76q+yTmbEUkCstJSVFnU1UeVSoklTxnOKjPcQDhlmIW2mxxETmBiw0PY9oywf3h4r60yPY8o1+Ru7eL7AtSYt5nSMQEajKSj3uRki7ghHPKzgUbbRMmLX/gP5+mdvxdVwmPFpHoGeYF4JD22qBMksLsFzwgoiIiG6v//73v/jjjz8QHR2ttpAhPT1dTqjoSlu3bp06m6jycGtgFGt2Xbx4UdbZi5abm4usrCyHffGboKLWYRSTxIhJaxpmbcMSNW35qOkH0WaY4xE9n36TMC7cB1nbFsnjJ6hJahaOaKlmR72G8DFT9WcUbYnJdF4ajCDj/SJjccJihlWvDqPwopzoRr+23kZbT3pjuldj+QxRwqofY6yxaMzgql9HnW+sN2mUuarrjHUYjomIiKgyEbMTz5w5U46OEREVh1uX1Vi9erXV0L4IhGIdLyMU2vaFYcOGyfUYKzK5lEZsCoKHzsALfVi4WllxWY3i4bIahRtbistqEFVU5W1ZjW3btslmEI/7tG1rnm/dmASnPCjNZTXEYMSbb75p+u+FmDtDPOMpJgey1xePUuXk5Mi1wYvyW+w0zN2QqnpA3U5PY8b4Lq7PtUFUipxdVsOtgZHsY2AkgYGxeBgYC8fASOS68hYYbQ0cOLDcllKWZmBMTU2V61VOmTJF9kXV24EDB9C1a1e7/dOnT2PNmjWm4+3LwI6ls7Hq5xwEPjoLrw66R21bhF/CpmCsXNuNqGwoF+swEhERERG5i6hmO3funGxiNFHM1m/ZF/td8ts2fK2FRTR9FCNkWBR80XXCXIxttBUzxKNEL6/F72oPfouV255dthPn1GvxKNLMtcYRImyOl9tGTViGnXKOxd/wyTT9OMtrZcQtxSR5/gRE6QdqLI61ugaR8xgYyyC5WH/MuxxdJCIiIipFosw0OTlZtmPHjhXou+q3fQcgClEDw9rDiIsmLdojpIn28+QB7FMpTz++LoJCW+NGajou6ptx6sA+PQhmHEZCkhZAhYtpSBcHZKTqPwXTtTJwJCEJ+pEXkSYPEGFxMTL6LNBn6Z/RD00u7sG6NVo4lccROYeBkYiIiIgqJU9PT3Tu3Fm2du3aoXbt2lb9atWqqSOdkYHTpiRnTwt0690RdXASCTLl/Yb9B7R4WbcV2rX2QXb6GS3w1UWrDq1QRwXBjMMJ+LVKJ0SEi6SpZKcjXUuGdYM7IKiOupYMllXQsW84zEe2wF/nLjWXwdbzh38dkTvT4eLCdVTJMTASERERUaVUsiWpvmjsX/jz4b5tQtBSC21yBPG3fUiQeVFfok1XD83//GftGBEE9+qjhvUC4F9b7MvG2VRzPWndln/Gg63qyGvtE8Eypx789AO1UJgqRxHNZapaey4a+9RgJZErGBiJiIiIqFIq6ZLUev6NoOVBc0mpLd82CNFCHk7GITp6h6kctaExOllXC4fN9GNOxa3DlqQcWd7aRl5XLzXNkKWrdRHg3wytQ8RoZBz+31dasGwahvZtLUYRf4vFkuifUaXT03hLlKS+PQrtxc0RuYiBkYiIiIgqpZItSdXyYHgfPCSfU/wSq0wT1wC/xc5VE9H4omufrmiiRb7TqWJynHBEyJLRbKSfMYb/fPUgeDEVp3OaIqT9PfBt4q9FRJ1euqrTRyz1a8nnJn2bwNEgpyxv5QgjFQMDIxERERFVOiIsiqUzjh49KptYG1yUojrqp6enIy8vT53tiHhu8G2M6FgHp76cbZqddNnZLhhiPEtoTH6jKTA5Tr0ANNEOMwVEMWpocYAoNdWfP6wHP/1AFRD1YGmSnYZU78EY3k+Lpnvew/PaPby49hJaitFNIhdxHUaiMorrMBYP12Es3Fiuw0jkMq7D6D6luQ6jWIR/9erVqgfcvHlTlqTWqFHDbl+oU6cOhg0bpnrFZazV6I2+s16HafUNotuM6zASERERETkgwt+YMWNMbezYsZg0aZLDvmi3HhY1xlIZ4nlF/u6OygEGRiIiIiKi28R4ltB6dlSissutgVGUApw/f96l5tr0xkREREREZYdv+AQsjonBO+O7oKHaRlSWuTUw/ve//8WcOXNcasePH1dnExERERERUWliSWqJycXe6EjTbFijJq3CAbWHiIiIiIioPHJrYKxSpYp84LhBgwayibVvvL29HfbFWjjinCJlbsA8I7iJNnoeNp9S+0pB5oa52vuMxfI4sb5OacjExrn6Z5myyjqG6u9tfNbRmL+pFD8oERERERFVKm4NjGK64qeeegrTp0+XLSIiQs5I5ajfrFkzeU5hcvdG4/nIWCR7d8fEmBhEa23pP/3w3epNKJUolbsXX25NAizeT7bFIxCmDrklMvxGYq32FrZEWJyb0Vd/vwWDEYR8JK55CzEc2iQiIiIiohLg1nUYly9fjm7duuHuu++W/f3798vXYlTR6AcHB6NhQ/2R4KioKPTq1QstWrSQ/YLESJwIV94In7wYwy0TmxbsVs5cgp22g4Ai6GnhLlALXy/EmlOZR+uhmDa1DwJlT5SbzrQZQdTfY9D1aLyyZDd8+z6EGxu/QbLFPuP9RYh9ZUkczuld7S0nY+EIbadxT9f0ewizc/8iFL6wpTGG9zqNGO3+TOcWYJzrgeChM/BCH/3OqfziOozFw3UYCyfWYXyx/z/QtEGA2kJERXnlsxV4PLQb12F0g9Jch5GosnN2HUa3BsbFixfLgOjr6yv7Fy9ehKenJ6pXr27qd+zY0fnAKEbjjNFFRyN8BUKaCmUWYcwIeLmm0KjCWEprDJ7xNG58YA51/VJV0PQQ+6Yior66/iW93yVdv9Z1dW39vVL0UNc1vcjAaLC9x4IKCctULjEwFg8DY+He+XY1ktNSVI+InDX5kWFo6ddM9coXBkYisqdcBEYRAHv37o3mzZvL/q5duxAUFGQKiLb9ogKjaSTPpcBoGQa1wCcH5my3qX66OKc/TlsEMz0wqgAoR/WM0chr2v65uHef8VqFOBVqT4gwOsEPX5dQYDT2W4+MUnnGwFg8DIxERNYYGInIHmcDo9ufYczPz8fly5dlu3HjBq5cuWLVd4VXM3/X17PJTUG6USvqiDrGo5E/nF9fNR/pZ35HepooY81C3CI1MY0YAdUPKDEiKL8pRjm1oPxPhkWqZMRSOzNnzjS1tLQ0+cslo79y5Up1JBERERG5yq2B8erVqzh8+DB+/PFH2bKzs3Ho0CGrvks8A+AvEl3WfsQ7O/GLVzP4F5EycxPjcTjTA3eFtisQxjwDArSQmo+0dNuHIz3g3+ge+AeIGxIjhhYT4mgtqoSCnVOjqkQV2NmzZ+XfG0YL0P4/efToUVNf7CciIrJ17do1+d8LV1pKCkv6qfJxa2CsUaMG2rdvjx49eshWv379An2XeHXAoz1aaS+yELfSYh3EzA1YOM/RLKk+uD9UOyf/CLZ8o5+Ru/cLbBMDdp0jEBGYi8T4QzjncTdC2hWMeF7BoWijZcKs/Qf098vcjq/jMuHROgI9w7wQHNpWC5RZWoAthalLtc+1lGGRyOSOO+6QJaldu3ZVW4iIiOxLT0+XFSmutPJa2kt0K9waGMWaimJim/Pnz8uWm5uLrKwsh33xm6Ci1mH06TcNSyeGo2HWNiwx1iecfhBthjke0fPpNwnjwn2QtW2RPH6CaZKalubnEccYzzfa0ELqyJcGI8h4P+P5RDWC6NVhFF4c3Mp0bbvrJZruVTy/KDcgbpF+jHg2UZwjJ9aRh4rriH3J2PvFVr281fKzam2sw3BMVLE98cQTaNKkiXw22t/fX20lIiIiouJy66Q3q1evthraF4GwatWqstnrC8OGDZPrMVZkVjOpcnmMSouT3jjnp59+wptvvol27dph4sSJpkmyPv74Y9nuv/9+vPgiJ0sgosqLk97YJwYjxH8/jEnSxNwZly5dQt26de32xaNUOTk5cm1wh36LxYzXNiC16aN4+fVBuEdumoa5G1IR+OgsvDpIbCEqG8rFpDci/BmL8os2a9YszJgxw2FftIoeFomoeMSarkZYFMLDw+U6rkRERPbk5eXJapQxY8bI9tRTT6Fz584O+4MGDZLLv7nmN+w/kKr9bIqQ9gyLVD65dYSR7OMIIwkcYXSOGGFctmwZhg8fLp9htBQfHy9nYuYIo2MzPl+Oc5eyVI+ICvPaY+PQsLa36pUfHGG0LzU1FR9++CH+8Y9/yL6YqV9Mlibm0zD6iYmJcl4N4fTp01izZg2mTJki+3bZjjDaGXE0HSNP0NTthJGzxqOLmoo/I24pXo/+GTl6V6rb6WnMGN/FzmoAGdixdDZW/awfXbfTYDxycxPWqb5ZU/Sd9ToG1YnDstnR2GfslvcVjlMW1zDTzpn4CNJWasd7W9y/ifHe3vq19eHUgp+XyqxysQ4jETnGwOgcoyTVEZakFu4vUc9i1TNzUMfDS20hInuGvzcd8/9vMhrVc36BrbKCgdE+ERg/+OAD9O3bV/bFo1AZGRlo1KiRqS9m7C9+YDSCWBV0fHoWxopEaBuoMlSAq2IOjXoJa45+TqOt8vgcu4HRCGzG9W9q/UX4JWyKem0T5uR7fY2AKXrfCKb1TKWydgKgcX/OBEbLMMrAWC6Ui5JUIqJb1bZtW7z66qumJpbVGDt2rKk/ZMgQdSTZc+nKZTRp4A9vr7psbGyFtNz8XNSpWUv9P4cqipo1ayI0NFS2li1bolatWlb9atWqqSNddPJLvD78OeuwqPlt3wGkoi469u6mhynfcER0bQJcTMLBI2KJtgycTr+o/awHvyZF/HIi4zASkrR01lS7hry+L7pOmGt6rwK09xq/TAVB0W3ir92J9tZpqShqSfKiaeFxzSfmkUuqUBgYiahc8/LykqHRaB4eHmjevLmpb0xmQEREZEuMIp47d042McGNKEO17Iv9xSJG2GJiMK1fHfz8XiRmrv1d22iEwcJkI/2MlrrqBsBfn2vHsex0pLsY0MTopWnWfsuy2KLIAGzMyD8BUTut1x+/tGcN1olw3DccWvylCoaBkYiIiIgqJTHzaXJysmzHjh0r0L9VLbr3Rvs6wKm4jdiZ6YvGRaXAjFSITFm3lb7Od6Hq+cNfu7azRAnqUjVba7QWZqNn9HM+3KkAHP32KO3zXMTPsWu0z6P24SR2bPwZVToNxpAOtdU2qkgYGImIiIioUhKznoqZUEUTyzPVrl3bql/sklSDbxuEtNJS3cU9+Hr772jRPkwLaVrg+mo7xJijeEZw845UU1npb9u+wr6cuggKbW1nghsbxrVPHsA+eTExgji3wOifI3p5bAmp2wkDh9qblIcqAgZGIiIiIrrNzuO7JVOwaIdz4aY0iLB48eJFHD16VDaxNrgoRXXUT09Pl0txuMYXXft0lSN5pw7sw+8tBmPiqI6oY5R4PmeeUOaGWq9RS5eyjNWybPTinvfw/Mtr9ZBpIp5ZfBZ9mpzExtl6ueiys10wxMEzjL7hQzGwYx2c+nK2PHZuQgDaOzvEaHm/OU3Rd7J5Vlct7dr0qaLhLKlEZRRnSS2eyMhITJgwgc8uOumRRf/ErpkfoWoV/v6QqDAPvzkKH4yci9oe5W/im7I1S2q2FhQjsehAWwz+cw5O126CM7Hfo9Gk+ZjctWDiKM1ZUsUi/KtXr1Y94ObNm7IktUaNGnb7Qp06deQ64qVBnx21qnmGUpPf8Mm017CpKmcepZLFWVKJiIiISM4evX79etVzt3p4aOJ7WPd2J6Tvisd3u2tj9Lpou2GxtInwZyzKL5qYYXvSpEkO+6KVVlgkKssYGImIiIgqsNdffx1btmzB559/LtcZvF1NlHMWJEYYn8bA5/bAv3MoHnrgEt4dOMqtpalEVDi3lqSKBVPz8/NVzzmNGzeWNedEFR1LUouHJamuKawkddmyZXLRaleMGzcO3t7eqkdUcZTnklThwoULmD9/PrKystSW0tewYUMZVu0TzzC+jj1h0wodXSzNklSiys7ZklS3BsaoqCj5ELErRDlAixYtVI+o4mJgLB4GRtcUFhhffvlllyd4EP84rJy/1NuHRXNfwX+q9sHKCWPwwLF/4+EP16N5z/fx7sO+6hgqz8p7YCyvGBiJSg+fYSQiorLpFy1MvTQAbYw2bwV256p95VZ7TB7QH42zN2Hk69pn0sLi6Xp9MKozwyIREZVvbh1hXLFihfzttfHb6EuXLsHDw8O05o1tX5Swjhw5Es2bN5f9gjKxcW4k1iapruLReiimTe2DQNV3SeYGzIuMRbLq6rwRPnkxhoepLlEp4Ahj8XCE0TWFjTDOmTMHTz75JOrV0/+3t2PHDjz44IOmv5Nt+8uXL5clqQ0aNJB9e05unYVBX+9Hzp3/wPYxj8FPbZuc0Q+rhtwPLvlMZRVHGN2DI4xEpadcjDCK6Yofe+wx08xTDz30kPzHiaO+eH5RnFM0EehiEB2jt6jihkVL3t0xUVwvaiK6+GQhbtEkxBxQ+4iIKiDxCz0xu6IIgKKJX+7Vr1/fYf/KlStFlKPuw9oftbCIdpg9WA+LQtMes7FWhMXT6zF+1gC0WfE5zso9osxTjEJOxyfG3BnGMcbopOlYYO/akdq2Z/DWgUv6BmMk03TMSXz67hDzuRbXFaH1AdH/wXL007y/wLWN+1Cjo/r5AzD6mwx9v717JyIiKofcGhhv3LghF0wVs2iJJta6ERMsWPZLQu7eaDw/XAt42zdgnlh0VLZiBj6vYIS0FQ9n5yP9zCm5KXPDXHVN0UZj/iZ9uyRGKG3e0zh+yir9BvS++Tzr6w3H2HmbYL5iLvZGq8VcTc3yPQvuN96n6HOJiMzE39FiFHHr1q2yXbt2DXFxcQ77169fV2c68MvP2JCj/bzzfoQ31De5RIS0d/+NrQH/wPY3vsDhv/VH4xPvY/jHP0HFuEKIsPgcNjdfhsPi3An/RI8aBzEr1hw4Aa3/ZQpGP6euLfpW+w1aGFyl3ccfqluAeK838R/xWYmIiMo5twdGMe3yqVOnZBO/nc7MzLTql5wsxK3cgkZi5HHBYATJ/irc6iChCHczD96HV+Vo5gIMapWPxM9WY7PIYEY5qzE6uaAXzmjveapbb3TRMmfWrs3YnLwXX25NArw7o1efQHm9F2KT4N19shwdXToxHF5H1mCuKTTmIT0tU9TZYvCcGMwf3Epu1YlAOBPL4y4heOgceb7Yn7VtkUVo1KhzC9wvEZGFKlWqoFOnTvjTn/4kW82aNdG+fXuH/apVC/9PysmzqbiVDHUycQ/2aCGtS8sH9dHJezuiXx0g5dheHCryGcim+Mvoj80T0DRujObiSYvs0zhmcW6Xns/iryLMqmvjxE+Isxkh3Lt2aaFh8OTW9zDvuGuTBREREZVVbg2M4rkX8TxiaGiobLVr1y7QL0ne3Ufqzx36PIAQkbOy9iPe1cSYuR1fx4nAdjdC2gXCp980i5JXT/gHaEkw/wzStUMyd8cjGR4IjngY8nFHn36YungEwrw64NEe2g3kH0HsnCXYmWkck4mf4rXwqAW6Xg/rD0h6dRiA7uLQY/H4RYS63BSki3+8eAQgwLbONjcRCYe0N1bhU/Axwun+A47Dsb1rEVGlJwKjKDGtVauWbGIEUSx07agvji9MU78mEBmsuM6ePyED585v/6FKRl+xE9zSsfLjJ/X9YuIZtVWymmzH3rlOOBmNF/eeQ5dOg9Gjhtpm6eJXeDNuPxqEDcaTt/JhiYiIyohKUZJaIrK2YYko4RQjhmKEbsZURIiQlbsXKyON8s6xWC7CpJSLFJns7DOCnGQEPCMMFiYvTYZRj0b+ME43UfuKJILqdHG/YoIgi0BLRGShxEtSGzRGsAhZdkbtnOHX4E4ZOLv0fF8vKzXa1DF4wEs/BvDHyCEf6dtlWakiylk/0QKkmGxHnvcKnnEm0NULxJ0e6rUIoz98I6/x2p/srzW5c08stnr2wSv928B0S0REROWYWwOj+MfFyZMnkZycLJuYYEGUolr2S5VHI/gXSF0OGGWlor2rwqKYlXXxEuy8ZJR4RmFcuHFBLzTzd/yQTub2r7DTCHdaGP1AlIx6NUMhp0i5Kek4Bw/cFdqu4EQ+ngHOfR5TSaq439pIXPMWJ/AhogJKuiQVjftjZDvxl5zNs4G//BsjnHgOsWlwJ3TSAufOX3+w81yhi4znKW3s/PYdfZIaY3+9xrjbKvlZT9hTkBZYI56yCLBEVFaJR5/27NnjUouPj1dnE1Uebg2M1atXR9u2bdG5c2fZ6tatW6BfkrK2rdSDUeZuJIilN1Qppj4pju3kMsVglIQqPg+EIgj5OB5/UL+uGI2cvQoHMjfgvVjx3KIWQuXzlNq9iecZT/ng/lC9VHXLN3qCy937BbbJRxwjtJCaibiv4nBOlcMWYEzIk7ULW4wJdGQw5SgiEbmupEtShQ6DVuKrR+5DnRPvo5tRHrr+Osb0t1hSw7TPKBvVAubbz+Cts92w7K/6RDemc7XWx5lJb7Sw+mK4xft+mIL7WxX8DV2XVvXw7ttiv76O4sq/W4ZDMXr5kv6MowNdes7F82FcHISoPBDzZqxZs8al9u2336qziSoPt6/DKAJikyZNZP/QoUNo2rSpKSja9j///HO5DEfR6zBar5MoAuErS+JwvUMH+O3dq6+paFFWauzPtbdeo+XENeL5Q7XZxGqdRg/c3aElLu49iXvV+xvX1quvxH3Nxb37jIlpZuCFPvXVRDWZcqKbhSNamvoGfXug3TUmLdk/TguL8n3EpzImxbGsW7XcT2UJ12EsHq7D6Jqi1mEUZanGyKF4TEA8e24EQ9t+VlYWXnrpJbnERkkSS1o8tbeaFtYWlVoYM9aHDOv5vnliHCILXIfRPUpzHUaxvvfChQtVzzni36xTpkxRPaLyzdl1GN0aGEUAPH3aPCWB+MfHHXfcYfWPE8u+MGDAAFPAdJYpMMpAVV7H2VQYTrcTXFVoPVuuPx/ZYmAsHgZG1xQWGEUAFIHRFd7e3kWXprqIgZHKAgZG9yjNwHj+/Hm8/fbbCAkJkX3x704xh4ZYf9Ze/48//pCPUk2fPl327fotFjNe24DUpo/i5dcH4R65MQM7ls7Gqp+roOPTszDWNIkFkXuVi4X7LRftF23ixIkYN26cw75oroZFIiIqHhH+jEX5nW0lHRaJiEqLmCvDx8cHQ4cOlU38u1Q8l+2o//DDD8syfaLKhv9lJyKiMk0893j4jf+U6rOBTXvMxu43vuDoIlElI0YRxaihaGJt8Pz8fKu+mA26VGTEYdl4Y5Z9rb28Fr/rO7Bj6Xht28tYq2/QRy0tjzH6WptpOsg4T9s+YZl5YkUX3icjbikmacc8u2ynepTK4pqqmd/vN3wyzbxdbxb3XODcgu9jupZxj+q+C+w3vZed70Q18z0X9FvsNNNx4vPvU9c3bVNNfz/7923ck+Xxos1cu7fA92jJqc9SDlSKwOjVYRTeiokp5+WaPug7LQbR9p6jFOs7lvvPR0RERHR73bx5U440iiZmTbXtlwoRkGZ/jYAp+uz7b47qiDonv8Qq+4kDy97ZgFTVFTJS03FRvT51YJ8eADMOIyFJTf18MQ3p4gD5PtHY5/0oXhaz/M/ohyba+ywpJFyZieBklNEukPc5rV8TnPpytkX40YjSW3Htt0ehfZ2T2BgtAql+7jeNpuirC1jtc5W41jvYZPkFqLLfnE5Py3/fi+/v5p73sNjO9yfC4twNqQh8dJb+GUL24bOMfliszhOrKxn7Xh1Ux+F954RPcHDOnfJ9nGPns5QTHGEkIiIiotvsPL5bMgWLdlhOxHf71ahRA0FBQbIFBgbKklPLvpjYq1i0YPa6aSTqOS14Wazj4xuO8ctexyD9AUf4NvGHmN7xYlqqTZDTAsaaT7DPZgmg7PQzyNHOaNWhlRY0D2CflpMyDifg1yqdEBFufnRLbtPODQxrrz9L2aI9QrTdF5Picbior90IoE3DEaGeuWzRvbcWoCxCqh11A/xRD77oOmGZFqZMHxD+4gNmpyHVxT/ujLg1WGf53Wl+23dAC9B1ERTaGmLSat82IWhp975+w/4DWjqr2wmPdNPvpcXgueb7KqDk7tsee5+lvGBgJCIiIqLbJFsLik9j4KgYpHp5A2c+xwsDR7ktOJZaSaox8ibb2xjRUYxLmVmVSYpJctR2S5f2iIBRBR37hqPgDB710PzPf9aC0kkk7NuLIwlJyKkXAH9ZuZ+Ns1rC0YOlFqS+nK3e6zU7o1snsXG2fh8vRv8sj5ey05HuTLYxgvFz0VqwbYqH+naRIc66ZNTe+1rclzxXbbSUswcff/IzqnTqiy6mLyADp+Xw6UX8/F5k4ednpOojra5w4r7tM3+PohUokbX7WcoPBkYiIiIiuk3q4aGJ72Hd252Qvise3+2ujdHrojG5q3tmDhUzQYvZUkUzZoa27JcG8VzbUosySVkqqvaZncSOjSJgDMaQDpbPb6vAVFcLh83aIKRVHZyKW4ctSTlyJLGNfyPU0cJUmnZMPfnaXD5pakvHwzxRa1P0naVvN8otpXr+8LfOuPaZgvEM9GmihaZFy7AzWZXRWu1Tx1sw3Zcs/VQbLZzavhH7qnTCwKEdzOv0wheN5bBfXVOprKmZZqVVjBFCZxnlv0Xct33G96j/cuDinlh8bHqQ1NFnKT8YGImIiIgqoAsXLshRMnc1sSRFQWqE8bk98O8cioceuIR33TjCWLNmTYSGhsrWsmVL1KpVy6pf7JJUF+gllnbUFQFDjdiZZCP9jDGc5ovWIa1Q52IqTuc0RUj7e0zlrXKvw1JNJ/jqYRQn47BZBZ/ftn2FfTlaUOvdzTqYFeW3fUhweqTOkvZeg4dahFtdi/ZhWsC+iOT4I0U8i9kC94Vpie9iEg4e0T+DCOtvOjvbTLHv2x77n6W8YGAkIiIiqmB27dqFSZMmYebMmW5rixYtUndjSY0wRg9Hk9wsoNFjmO+mEUbxvKIYRdyzZ49sBw4ckKWojvrJyclyMpxb5Rs+FAM71jGVZM5NCED7AiNZTdF3suVIoI16AWii7TMFxKZh0PKiiXweUjwr+aw+0Y35ecrCZxQ1E8/zPYs+Tcyln3M35BRcR9J0bVG+qe45KBxD/qpP5CP3vZYA/w5OD9WZBD462f6alS0GY6Ka6OZ59ZlEs5qMR2kxeDJGdLxp+gwvft0If3X0DKP2fRX/vo2SVP15Vdt7d/hZygm3LtxPRI5x4f7i4cL9rils4X4iMitPC/eLsLhy5UrMmjWr3K9fXZoL9+fm5uLLL79UPX3GVPFMo5gIx15f8PLywqOPPqp6ROVbuVi4n4iIiIhKlhjZqwhhsbSJ8Gcsyi/aE088gb///e8O+6IxLFJlxMBIREREVIFcv36dYZGISoxbA2NiYqKpLtzZlpPjzBy/REREREREdKvcGhi3bt2KNWvWuNTS09PV2URERERERFSaWJJKRBWKeCZFTGRQuR3HZ9OGYODASfjv4atqGxFVVLt378by5ctNrUqVKlZ9sZ+IqLjcGhjFX2jBwcHo1KmTbGJWw5CQEIf9OnXqyHMcy8TGuWJK20mIOWBs2oB5YmrcSatgbCKiiks8t7Np0yb5DE+ltDsKwwYuQs4jf0Wr0l8+jIjKgJSUFFm1ZbQGDRpY9cV+IqLicuuyGlFRUejduzeaN28u+2Ia6KCgIDRsqC9RatsXx/fq1QstWrSQ/YJEYIzE2iRvhE9ejOFhIi/OxQuxSfDuPhkLR2gbiMoJLqtRPCIoGmt/9enTR/6sqMSi0pbTvVs5/hmmvbgNrWe9jafaVFcbC+KyGkTOKcvLasTGxuLjjz+Wr0WVxTvvvIMZM2YgLS1NbhsyZAgGDx4sX5c3pbmsBlFl5+yyGm4NjEuXLkXHjh0RGBgo+0ePHkVAQID8y87ot2vX7hYCY8EAaT5GnqDxQPDQGXihj34PyN2LlTOXYGem3pU8WmPwjKmIUIdYyt0bjVeWxOkLoGrHPTbQD999qPoW9MDaEnujZ2J5nHFx/b4GXbe4hgXv7v/C326s1Y6/ZnH/ZsZ7XzeFYXufl8orBsbiE6HxvffeQ2pqqtpSMU2ePBn169dXPRtlIDAuW7YM2n9jVM8548aNg7e3t+oRlR3lJTAOHz4cjz32mPyl+1tvvSW3MTASkT3lIjAuWbJElqT6+/vL/tmzZ1GvXj3UrKm/l+i3b9++2IHRCGK5rYdi2tQ+CCwQqHJVgLtkDo2ihDUyFifkOZ2QII5PsR8YjcBmXL++1n/j60b4l3ptHeb09/qw6lN63wim17pj4uIRkEc4OMe5wGgZRhkYKwIGRrolZSAwvvzyy8jLy1M957z++uvw9PRUvcrkAD54dhG239EV42b/Ax1+i8GURVvh99e3MbW/rzqG3Kk8BMYHH3wQEydOlJUHf/zxh/x31g8//MDASER2lYuF+6tVqybLUUNDQ2WrXbt2gX7xZCFu0XBMsAqLmszdSEgSA4ER6CnDlBc6DOiBIOTjePxBnNK25Kaky5E+j4BG+jkO5SIx/pB2rDceiNCv79VhFF433qsA7b1GLVBBUHSbwV/k4Pw0pIk3vkW5ez/GGtPIJRFRBXZAC1Pi2XSjRb6PvZf0XeVXGP4+oge8M3dg+TjtM2lhMcunKx7pxrBIzhHVWeHh4aYydfFT9I2qLSKi4nJrYBRlY2IU8eTJk7JduXIFGRkZVv3iESNsMYheMBh3HlmDmWrCGyMMFiYvLU07xgMB/j5qiyN5SE9zMaAZE/DIZlkWWxQ9ABv/OBo7b5MMtyZXkhD7kQjHfdGjldpGRFQGiBHDBQsWyCYqRObNm+ew78zI4qlNb2KsCFOt/oo3Y7S/57X26sOZ+PTjn1H+M+NwLFSfSbYF/0CH4v7elCodUcpdq1YtHDp0yNRE/+6771ZHEBEVj1sD482bN+VC/OfPn5ft6tWruHjxolX/lvh0wyPhWvDL2oUtm07Bq5k/9OJWR3KRkq5FSo+7EdKu8PFFwBP+AUWFSguiBPWNWCR7d8dE+Y+BBRjkdLhTATgmCuO0z5N/5DN8pH0eQ9YPG7HzUmsMGNYTDdQ2IqKK5wC2fnUY+WiFgc/0hzH2FtjnRbz+j46ofWoT3ho9HKPmrkeG3CPKPMUv2uZig75BJE79GOOXd6ZjxcDls9q2SKz8WUVPYyTTdMwpbH5ztPlci+vKICv62y1HP837C1zbuA81OqqfPxzz1pvupuC9ExVCPLMtJrqxbb/88os6gmyJkvmvvvrKpbZjxw51NlHlUUFLUg1eCA5tq4XEfCRu/gYHfB5AiBbS8o9sxrdyjY1c7P1iK5KNstLM7fg6LlPLi6G4t6i8aLp2FuIPqAU7Mjdgoe3onyOqPLZkeCD48WF2J+UhokpGLqsxEAMj/4uka6fw2Yyhcj3G9b9fUwfcPjdu3JD/wFq/fr1s4peAtn2XHIjHgQvaz1YhuL84lZoipL22BkeaqdHJyT3gnfQJ5r/vzOikCIuv4UDb1/XRvzlD0dojCev+Yw6cgNZfmYqeb6tri77VfoMWBt/W7iNfdQsQ77UC28VnJXLC/fffj/Hjx5uaYNkX+6kgMTixZcsWl9rPP/+sziaqPNwaGMWaiklJSdizZ49sx48fR0JCgsO+GI0sfB3Ggrw6DEB3MZKXtV8Ldj7oO2kiuvgYJZ5jzRPKBOqT3SRrh+aLMlb522FVNpp/BLHTLdZ2VMQziy8OboWsbYu0Y7Xjpx9Em2EOnmH06oDBT4ajYdY2LBHHRm5B7Q7ODjFa3m8mvLuPMc/qqrHtE1El9sBYrF63Duus2mL0v+f2L8pYtWpVuXRS//79ZatevXqBvitOnUmDw4zlhFMHE3BMu0BQyAP66GRYKMLqA+cOxyOpyMQYiIgX3zVPQBPYCP6igvZcOk5YnBv012fQTxyiro2kBPxkkxgPxKwqNAye2vQhvjh8K5+UKhuxbnX37t1NTbDsi/10m/wWixny35CWbQKirKbfJypf3BoYxRqLogRVLJ8h2rVr13DmzBmH/WbNmsnF+x3TAuE0UbppOUOozTYtuI1cIPpGs55NVCx/Yd6nt/laKHTEp98087HvmmdSFWHyLW2baZIbjbFNP34xxk/Uzi30HH2iHNP1VTP2Fzze3ucnIqoYAhsFwEO9Lo7Ms2dk4Ez+5Dn1j7hFdoJbJnYuHafvF89Kqq2S1WQ79s51wtEP8cHWCwh6uC9a2/swF7bif58dhlfXvujsYMUUoorhPL5bMgWLdrgvSInnpkUTz1OLJiYJatWqlcN+165dnZ/5uemjeNn0b7elGNvFhceYiMoYtwbGnj17YujQoab21FNP4cknn3TYF83Pz0+dTUREZVmJl6T6+KGRCFl2Ru2c4ePXSAbOoL++bfoFnGxWk8v4oMuE5fp2WVaqiHLWFZaT7UxGN2cCnY8/Akxz+WhhdOMP8hr/6F5XbbOW/M1GHKndFUOHtELJL2ZFpes4Pps2RJaA//fwLc7BUKFla0HxaQwcFYNUL+3/YWc+xwsDR7klOIrw16BBA1n5IFq3bt3kcm+O+p06dSrmsj8Z2LF0PEa9vBZxsdPUL520pvV/N/ZZjUIa217G2r1xWDZeHW/VtH2/a4faHdHU2oRlpjXFf7N8zyJGOzPilmKS5XW09uyynaZJI233z5Q3IXfo9yk/k9xQ8HMZxxjnG8can8Gmb3pfy35x3sf4rgrbV9g5Vn7DJ9MsjzOaE+/v4M/K+JzWf07W37u7uTUwEhFRxVXSJakI7INHHpR1ntbPBh6IwWtOPIcY2C4Ed2uJMTlht/nc4jKep7SR/Ml/9ElqjP0N/XGn1eP41hP2FKQF1ieGcHbU8kY+O7wIOY/8Fa1uf/W3FbFgf/36ZXl4uh4emvge1r3dCem74vHd7toYvS4ak7u6ZwROrFeZnJws26lTp2SItOyLarcSc/JLxCS0lyOP0/o1kf1Va3PQOqQV6uAikuOP6AEh4zASknKApmFof6c802LEcgb6aKfaqtvpaVl1Fv32KLS3KMYTIWTZ2T76PnnuRfwcu8YUJm1lp59BDuqi49MLED2jHyzfSoTF16N/Rr1HZ8lfqonPcOrLRYUGUBMRomZHY5+3+hzi2trnXyJCUYvueKSjdtMnD2BfgZCmBcJNO5Cq3VNQaOsiJq/UGO9TpZOqKBSf+SQ2zrYJgKbv83UMquPkOZbqGse+jRHi3g2FvX/VwXjN+Ozaocaf2Tvju+CC9uc0d0MqAtV3++aojri55z28VkZCIwOjwacfpmp/QJYlpAa97JRlnkRE7hY2/B28OrQNPJI+wYvGb2L/ew19h3SEKWOZ9hllo1rAfC4SK9O64Pkx+kQ3pnO19rwzk95oYfWJxy3ed1Eq7ulQ8B/lQVrS+/Y5sV9fR3HcRMtwKEYvJ+rPODoQ9NepGNmRabHckc8OL8ZTdxedFs+dOyeXECuNFhcXh5UrV2L27Nnq3Qq6cOGC3XNLo4nPWpAaYXxuD/w7h+KhBy7hXTeNMApibgyjNLVmzZoF+iWrKfqOGoR7tFct2ofJ0HDqwD7khPfBQ1rnYlI8DmtfQ8bhBPyq5cXAsPby2FvRYvBcGUj0oFUP/o20cHMxDekX5QYbGTgtd9SDXxPbAJ+BIwlJWphsipD2+l3pn8Ei6BaiwGdq0R4hps/sq0LzSSTYJkZTeA5HhBNlvab3Ce8L/fAW6Na7o/1rK8U5x5HiXes37D+QKkPoI93079bX5n8T7lYlOzv7pnptZcfZX5BxJVu+HhrUA57VWRxDdDvtSj2ExKwT8nVXv3vhW7OefE1Ukh75/9u7E+iqykPt4w8oEAQhYjBBkotWZC5BgVrvFSJqkUG0LRRYlRbI8mqlgiJOBQFFQBwYVVhabzB+1g9S+VYVmbQVA225yiABkbFVhECAqGFICRX02+8eTk7O2Sc5CZnz/631LvLu+eyA5sk7zb1bG6a8qfr1yv/3h48//nj0431cZt3GsnX5iswsabHggwussPZkhYUxsyzGzCWf6T9+8XzhxDioVW55JlWvj56ppjEXuVt8fPEnTXx0rTpOfV6/6uTfgm7+XfgHqfMXExOjhx56SK1bmygSzrQ+Llq0qNIW87/00kvtf9P+zBjG6drYbWKxrYt7j+zXGx+v1Nw7H3W3lB+zFMnSpUv14IMP2nUzr8bWrVvtsYp+9UOHDmnJkiWB432ZbodPrVC2acGa7oRDK0Zo3QtP6rVNsRowdbqGmI0hx31ntzCdVI+7xqrL1gWFx3qtX6Zlzr6e6RL5lFZlW+HT7P/Ouc7JnndpsgmGwS1cU+9Tr+/duhViCrnnOg8XxL32SffcvOBrt9IH9n3dQ4OYlrLJw77T/w27j2FaK6eq7+E5dgtaGNNSZ+5l/RXwWjDDLhH8Lr3PV8J9TEvdNPcDBreMTks5EPI+nVbYYs8p8qJC3lGc972tF939zTb3ex/xe2b/cwi9j32pcvevMwX65aKH9XrqDHeLP1oYAQAVInjR/mhLeYdFoLox/y5MaKuIMnfu3GLDoml9fPrpp33PrYgSOSwaLXTDuDlV1hXVU6ldUn00S4iX+XWw11q3KeM1ved1Rw3OKWVihY65bhDx6z4Z6li23fLYrH2yOoV9W9zWSTtsmmsVlsIWTEugq2fRezWPbyVT87pcBsoLThgyoe3RtD1qH9QV1u6yabrY5i3X9KAxmbYS7lMaZTknkjJdq2VrxfsPa682CIwAAAC1nAmTU6dOjRgoURkOaGWaM1nLvi1bZdrbmiW0dsKWN47vRLYOnWymHrfe6LZOliOve2cE+9au0Rbr3v5jBYvpNhqFlp266mrr45kuuGFnH8vU6nWmS2Z7/bBjSFJtmaJ+ve2+mdq+s+S+mYH7ZK50A+Y+fbhmk04GdfcMVZZzIinbtdrqmm7mM27U+x86b+dY5ir91XolTtfWs1o7zwyhSNXC9dLZD+bZwyn++yW74izXl/qS/mqfWTEIjACAWs2Me0xLn12hYwMT+z+qhenpdEdFtXXu3DnCoo+GDRvay7yZkpiYaPdyCK5feGF5zmKUpGsv26Lp1g/4ptuiaUG7P9Dd0QtkFr/gVCZt9YvUgWptBZHFE6xQ8dBbym/n3iOE1y3TSi3a9OoEZ4y36TJrtmx8VQ8//pZOpozVWHuimycDY8BLmnU1wAp+9z3gTHRjPr93vpkJdG/YuL+iAq2vaz4MD5uhvPt4n3lkFN06y3JOJGW8Vtuh4+2WUu/dPurbHbbqMIYRqKYYw4jKUJFjGIHapLzGMFaVwYMHa9myZW6t5qjIMYxff/215syZo169etn1M2fOKCcnx173269eUFCgTz/9VJMmTbLr0fMZw+gndGybu7kyOIGxvs/zuWPp6geNI0StwRhGAACAymAvqzFYgyf8H+0+e1B/mjzcXo/x3X9W7Pg3nB/TmuiFRcO0Nga3wobWzaRCwceXt7BuqkA1QWAEAAA4H/ayGsvsFrzCMl+3/aCKF2VEsUxg9BblN6Vfv34aOHBgxLopvd0ZU8vfPmdphaBlK4DqgsAIAAAAVJiW6j32RdmLxEfMgm31i5lm1s/ijqk4Zr1G/3u7z0V31DqtSgPjxo0btWbNmlIV098cAAAAAFDxqjwwvvfee6UqBEYAAAAAqBx0SQUAAAAA+KrSwFivXj317NlTffv2tUunTp3s2aci1Vu0aGGfE1muVs40a57cr/St7iZL/uY0PTxypMbMWqWD7jYAAAAAQPGqNDB+//33dmD0Zp7yAmKk+iWXXGKfAwAAAACoeFUaGM+ePasDBw5oz549djl9+rQOHjxYpF4x8rU5bYJSR5rWyKItkl5r5IOveU2Uoa2WXt0q978m7yjvvNSR9+jZVV47Zinuk79ZiydYx9wzS6vd0wuv6Zag++WumBl0XacUPnP4uWH3CVzLe0b3ucP2F94r/J24JeiZw+Su0CzvOPP5N7jXD2xzi3s/3+f2nilou12sc/439D0Gi+qzAAAAAIikDo5hNAFpiv5Q/1dKS09X2sJx6hWXp8zFhaGikDn2ab21260a+ft15Cv367xPlGWflK9dWTvkbC5QzpFce5u5z0uZZ5Uy3kyTPFtD2lv3WVRMuApigtMTCzKV33G4ppnnnD1U7fLWakFQ+JFi3Wsv1G9T4pS3drEdSO1zX6+vO815IftKy1zrmYzgF2DC4gS9tb+jhs5w31/Tncp4zuf9mbA4IUN7YvtonP0Z+urwku26ZrZ7Xpx1jLdv/ihdHem593bX6Ajn/NC+UXTCPwsAAACA4lRpYLzwwguVlJSkdu3a2cUsoJqYmFikXjZWMJtb2BI11gpeXsaTmqh76mzNGdXNrbZR/KXWnwU5ygkJcvmbl2pJpgl/QU7nyOTBmB90VxcraGZtNQltl7btOKUOA25RO/cwZ5t1YOw1SrZvFacfJbe37vO5tm0vKTF6ATRW1/Xrr0SzKe5G/cQKUIUh1UdMK8VbhzTpnqrnrDDlfMImauN8QB05HEVSDZa/WRlvBr87S+5H2mZlrpgrk9XFPFiTDura2f+5cj/K0h7FqEO/W5xniRuoxwLPFa7cntuP32cBAAAAUKxa2iXVa3lzygvjUmSiR0CRbpITirYges7stgNGfscBusnKeaFi2vRUihWU8j7Zqv/dlaXPcmMUH9/C3leQc1gH3WAp0yro3usRn9atvLVznecYs0DrA9n0tI7khARVX14wHqOXrGAbe30/9bPTZdEuo373LXwu59xwZ7Rn6Ztaf6qj+t1S+ALy9x+xQ1fBziWaUuz5+dofaIqNVhTPHUHgPZoS1kXW/7MAAAAAKF7d65JqxrU9HdRN0u4q6u4Lkvf3lXbAuH3EzXJioMMJTDFKiE9Sh+TOujRvg95dtkNfmZbEngl2C1/B4SPKbex8Heg+GSgv65H+dqqzxfYZ72z3ulvaGis+IVApRmEwfnZoeys0LdKzq/a43WiL7gsTeC6n62eYvL9rdeYpdfjpCN0U9AKatIm3w3eM11U2UOZrZJGmQ6+FMFpe998SnjsC7z3avxwo2Kl33giaETfCZwEAAHVXfn6+lixZUqqyfPly92yg7qilXVJLwe1iGS7GDhhOi12h0zk5gW6NTTokq1NcgQ5l5yr2mm7q5nVvdXZG7KpZsiZOGFWePlrtBp/cD/V+Zq4V1Prp5kh9On3l6uOs6FvqgsV0/Kl+GRRubXHXqauV4wo+z9KnJfQUjbsuWe1UoC+ytjufwYT1J/3Givop+3P78f0sAACgzsrLy9PGjRtLVfbu3eueDdQdVRoYzZqK5h/fmjVr7PLZZ59p/fr1EevffPNNCeswRqFJdw39ZYou9bpkTnhPTbuHt2TF9rm3SEtgUTGKb2XtCwTEWCV3C0px9nhIM1byd85EN0HjKYudUTSIGc/36ND2hV0/J2Toy47DNfExd0yjrfDapvum88zt1H3YL52JfOx9E/Tnpt0Lx1ZGK7aP7i5yL0+cBtzvTnQzyf1MphSZjMcVN1Bjx6WoifcZxryu+ndEGsNova/zeG6vS6o9XjX02SN+FgAAgOgVu7zbvgxN9n4uCiuP661/uscBNUy948eP+/7NX3f0Ux07c9z+eni7m9S4QSP76/JkwuLXX3/t1pwxjRdccEEgFIbWDbNuo1nAH6jtNmTv0K68L+2ve1/WRS0bNbe/BsrTT+berQ1T3lT9enVvhAJQGrc8k6rXR89U05iL3C01y+DBg7Vs2TK3VnPsPbJfb3y8UnPvfNTdUn7Mz6Dz5s3ToEGD7LqZO+PLL79U+/ZOQ0Jo3XRh/dvf/qZJkybZ9eLsy5iomSuylThoqqYN+YG7Fahe/nWmQL9c9LBeT53hbvFXpYERQGQERlQGAiMQHQJj1ajIwJidna2lS5fqwQcftOsnTpzQ1q1b1bt3b9/6oUOH7HGM3vHFCQ+Mx7TuhSf12qZYDZg6XfYm0yL51AplJw3S49OH6Dv3nFDNet6lyff1KjqBo+VY5guanrZJJ9263Os4ly7pWt7zeGcnBZ7Lue4R9RrdVVmLrecL2W8UvX4z9bhrqsaYyTjcz3TSu8+xTL34ZJq21Oup0VPvU6+4ffrjxKe06qRXL/wc9exzOmhHCe/JfQSUg2gDIz8hAAAAoE46c+aMsrKy7GLGJ/7rX/8qUje93SqECVLzvDAWzISv2fZEfs+k9tDF7tZQwSHrOTP54OSBan1guaY//pYKe75GulZweDUTDU5W/9YHtHLui0Ez9lv1xduUbPaba5t6mnNtExZfPNrfua997gltylgSdG4pWGFwQXDoDRXxPaEyERgBAABQJ9WvX98e6mRKbGxsWL1iWIFtyR+1JWJKKskx7dy22wpZSbphgNvy2LaPftLDioQHtmpLSWMlj32mbbutmyd107V2c11bXdOttXRit7bvLEx9iYNSnRa+tteqq7Xbu3bboTM1L9Di2Vzxraz7nsjRkRP2hlLYpz+mFRcGz/c9obwQGAEAAFAnNWjQwJ6x35SWLVsqJiamSN3M6F/eTm1comWb6qnHgBSZHFZ6x3Xk8HmkqONHdMScblok3Ul5/LqvRmRa/e7zJvN5KKhba+kcfidNq7KT1HuAf0vq+b8nlBcCIwAAAOqkyu+SekDrVpqupEM1rHtTd1tpua16ZdU8XvHmdDMm0O5W6pUXnHGIkTRLUHyzffrjXHdM4mxzzvMaZVo2S+vERq3ONGM8UzUwwd1WRHm8J5QXAiMAAADqpCrpktqspwYPD5/EJnot1bFre11shaq/rlzvrA++b63e33TSuvSt6lPSrDAtO6lreyvkldB99eDyNGcpkH1btM00QDZPUOvQPOl1by0LK7CO8mbR8XPe7wnlhVlSgWqKWVJRGX628AH9uG2yLmoQ424B4OedrR/aMwm2al5MC0w1xiyp4arnLKknAzOOFp09NDw4hc6EGjybqrOvuGu5s5UG90S1ApqZubTDDufY5t276/vNm50xhu4+uwHSe26zXc3UvnsrHdr8L/Uyn+u74H2hzEyro/T9q8ySWl2wrAZQwxEYURk+zd6nf5/71q0BKE7ny69SowsburWahcAYzqzD+Pzzz6tr1652/dtvv7W3xcfH+9b//e9/68CBA1Gtw1iTeQGuebmtIekTllEtEBiBGo7ACAAoLwTGcGb84rZt29xadBo2bKjk5GS3VjsRGOsO1mEEAAAAImjUqJF69uxZqlLbwyLgh8AIAAAAwNYyZazmp6eXU+ui0VK9x76otHRaF2uqKg2MGzdu1Jo1a0pVTF9yAAAAAEDFq/LA+N5775WqEBgBAAAAoHLUsi6puVo5c6RSRxYtY2at0kH3CAAAAABAdKo0MNarV88eQNy3b1+7dOrUSb169YpYN4uomnNKFquU8elKS3fKwsf6K9HdAwAAAACITpUuq7Fw4ULdeuutuuqqq+z6hg0b1K5dO116qbM0aWjdHG+CY9u2be16ONPCOEFv7TaBcb5GdnO25m9O0xMLstRldF8dXpyhPfZW55gh58y+TOV3HK6JbrB0js/UuT6/0Z3fvaWXMnPtM4LF9hmvOaMS3fu5GwNi1GH4ZD3S37pa7grNmuDd09oTdJ8w+Zu1eMoCrQ++XUxHDZ38mPo5D1Z0f2wfjZs/St2Ur81pU6znPBv43N5nKPxc3jGBk91jQ9+ZW9/v3Te4PlYt3yvtfbx3Zb4ZkfZdXcw5ReWumKlHMsJeeNB7jXSPCN8r7/3GFP0+Bb/3wr8PzjN5z+A9Y9FnCvrenyeW1QAAlBeW1QAQqkYsq3H27Fl7AdQ9e/bY5fTp0zp48GCRevnJU+bi99TKtDzOHqp2dv017e2QrE5xUsHnWfrU7rear11ZO/SVFaiSuzkLuTrhymmtfHZoe3dbEBMuZpj9C/XbFOtiHhMWJ21XN3ufc27Bzj/pzVUROsieztERK+eY8DMtfbaGBN/KC4tnrZBoWk7NZ8hbq1ei6m4bHCjNs5hrW59/0SytPhinlFtTdKn1PrK2bnWPL5S/+R2ttbJQzJXJ6lJiBvLuc8oKTTMCnzlv7Vw9+FrwtQvfZ2FYLOmcYCaUOce+MM48u6e4+x/UgIneZ7cO9b5nLweFRRPArXPSFo5Tr6Y7lfGUeT/OlQvl6uMs80I6qu8tTlicsv0a6/vlXbtAu/70hs95AABUnh07dmjp0qWBYgTXzX4AiEaVd0k1a+A0btzYLvXr1w+rl6fYPqOdVse469TVhIa8T5S1t7sG3WRVCj7Xtu3WT/n5u7Rth5XaYq+xAqN9WtnFDdRjJpC4QatxQoIVbgqUY1Khj/z9R6ygamWRhFZhLZD5u7L0mf1Y3WQ/lvsZCoNuMcI+U5x+lFz4mZu4oTnvk60qGtEKw/N1/SK0igYL3Od69XVb2OJuvFW9fK/tKss5kZTxWrkfZWmPCaH9bnHebZOQvxPBcj/StqAAHTdwYlCX58aKT7BuVnDYDv5ATfFp9j5t+XInhVLny5mz/3b/VdR8JhBmZGQEillwPrhOYAQQrTrUJbWwS2HYcYlOC9OXHYdr/E8O65XAsV7rV2EXzKLdEd1ujoHum8EtXKZb4iVuvWh6KL675X733Jgi1+6R5d8V0+k66XUVDU8pdlfNu77TG8HdLQOCuk/6dYe1Bb/L8O6eniL3CXSVtQS3jM7/hc6FvE+7FbbYc9xtrqLvKDHwvbW7xJZ4f7MttMtt6PfMiX7B9/ntZe/Z9zBh3ijy/fN9b0X//pUVXVJRWX62cLx+3LarLmoQ424B6p53tn5od8tq1TzO3VKzmVDotSxecMEFmjVrlp544gnl5+fb24YNG6ahQ4faX1dndEkFKk60XVKrNDAuWLBAXbt21eWXX27XTXdUEw5N66JXT05OrrjAGDpOb3eMLm/dVIeyvUDjhYmyBcbU7173DTeFzxHMPfejlkWfyb12ryNRnBtpbOHYy/R+hABmc0ObCcwTH+upbYH7ekE0NACX4j4lBUa/cFjWwFji/c220O99+DVD7+MFRvvd35Yd4V0Ff/+DPt95IDCispjAuPqhl9XgwgvdLUDdc+eiRzXltntqZWC84447NHLkSK1atUq///3v7W0ERgA1YgxjZctbu1jppl+i261QMQlKsPOBN46vwAqLuYrp2E83n+cP++G87p0R5H6o9zOte0cYKxi522gUmnRQ1872ycoKO9kKOe98YHfJvCL5hyHdTpuo++03qZ31Xr7I2l7yWMnAfTboPXecZu6Ha7Q+N6i7Z6iynBNJGa8Vd12y/Rl3rf6z826tkLn8A+svSFDX1oC4G/WTlDgV7Fytv4S+S69LLAAA1YT5xfygQYPsr6+77jq7DodpbV2yZEmpyvLly92zgbqjSgPjhRdeqKSkJLvbqSmmZTExMbFIvTzFdr9Kh+eOVKrptmi6cj5c2HrlBTLTTTM8OJVN3MC7nUlQlkxS6sgx+p8DbdTFvkeIoJlUC3Yu0RR7/cgJzoyeBTuVMel+pe/trtG/cya6WVDqNSat4Jf6O2eiG/P5vfPvmaXVe8LH/RXhjZX0C0hhvPt4n3lkWMtduLKcE0kZrxU3UGPN5Dneux3j37rpaKIOyZ3tSYI+Wr1RXe+2vif298ic94oOtvlh0CQ8AABUrRtvvNFelswwf6akpNhfQ8rLy9PGjRtLVfbu3eueXQfty9Bk6+ekB15cbzeA7MuYaP2s9bje+qezG7VXlXZJXbRokS655BK7GH5dUoPrmzZt0vDhwwNjHqNVfFdQT3hXxUrjBsajPs/ndI08Ui5dHFGz0CUVlYUuqUDt7JKamZmpKVOm2GMYg82bN89uaazrXVKzs7M1Z84ctxYdM4xqwoQJbi0yE6Zmrsh2a1Kznndp8n29avwvlWvr56qrakSX1B49egTCopGQkKCYmMJJF0LroceXq7BuqgAAADVXTk6OxowZo3vuuadI2blzp3tE3WYaJC6++GL7HZkyatQo3XDDDRHrI0aMUEFBgXt2JMe07oX77FCVOGiqvcRXWvrz+vn3q7Q0fGbBGqft0JnuZ3LKPMJinVClgbFnz572LKleGThwoPr16xexborXraK8OUsrqHDZCgAAgBqqc+fOdguiV4zgutlf15n1vps1a2b3XDOlTZs2ds+2SPX4+PiSh0vtW6v3N52UkgZp1JAfuBtbqvfYmRrTK07HMl/Q/SNHaorXj9Pt5pn6+FvyenZ6x3hDiALHap/+ONHaNvbFwOzsTrfQoGOOZerF+wrPLbyuE2RNPdM9p+j+8Gt7z+F0QXXPD+6C6vPsqJ3qxKQ3Tbqn6rl0s0h85Cho1tMzvykp7pgKY9ZrjHBv57nojgoAAKJnAqGZCdUrRnCdwOgwodEs42bK9u3bderUqSL1s2fPukdGZ9+WrTIdNhO7XSsvLpaGCWnT0zapuds6OXFgax1cPlcLo2mdNGHxyfeV8KDT+vdMag9dfGC5XgseZGjV07ddq8fda5t6kf0eKwwusJ7Dir7+zL3mrbA/K2q/OhEYAQAAgFANGjQITLZ45ZVXhtVL55gOHTnhfl0Wx7Rz224rpCWp67VO3Gx7bTe11gntydoZeaZ9T8sU3ffidHkNmy1bx6uZ9eeJnOygc5M0IHWIHWada0sHt24JaSHcpz+mFRcGj2ndkj9qS8Q0idqGwAgAiCgrK8t3psDiypkzZ9yzAaB6MzP2m26npjRt2lSNGjUqUjf7o9dSl8ebiFZWx3XksElhB7TySbfL6FM+we3ERi2e4OwPnoDG8LqoRjw3CoffSdOq7CT1HtBDF7vbgp3auETLNtVTjwEpduBE7UdgBABE9O677/quRVZcMWubAUBNUN5dUpvHt7JDVnirXTSaK76VOTtJA6YWTixjSpHJZZr11OjZzna7W6nLdGd9IXiynckDowp0zRLirTu7rDC6OtNcI1UDE9xtRRzQupWbVK/nUA3r3tTdhtqOwAgAAIA6qXy7pJpeof11g0lpIWMD92XMjGIcYkt17NreCpwHtG1L6eNmKG88ZVEHtDLNmaTG298soXXRmU6LTNjjwwqsg4czO2pdQmAEABQrOTnZntXaFDNr4LXXXhuxbrpzReXYn/XotNvV6XdBZf5SfeHuBoDKUL5dUo22+sXM5zWqx8U6uPzJQPfQF4/20rBehWt8BvZ53UatgDl97Iva1XmsxtoT3RSemzpybFST3rRMGa7BQfeduS1B14Y1MSbp2su2aLrZvyLbXkfx/uBwaFovH3DGOPpL0oDx9ynoo6AOqNKF+wFExsL9qCzFLdw/Y8YM3XvvvYEljf7yl7/o+uuv10UXXeRbDz3ez5G/zdKQd/+urxLu1Mr7h+kKs3Hf6/rZ/7yl3U37aOFvx+vGWPtQoNLUtoX7Qw0ePFjLli1zazVHRS7c//XXX+uZZ57RFVfY/xXSd999Z3dJNUtt+NW//fZbnTx5UpMmTbLr5ccsafGUVp20wtrUigpjZlmMJ/XaplgNmFo4MQ7qthqxcD8AoHozPzAdPnxYBw4csMu5c+dKrBdvl97eYIVFXa3Hfu6GRaPtrzXzx0nSqbV69e9fBFogR6z8QK88X9gKOWKl2wYZ1kI5Qa8fcHYBQDRMELz77rvVt29fu5i1v4cMGRKxbtYHN4v3A3UNgREAENH333+vvLw8+zfxppgAWVzdHF+sfR9rlZnfPeFH6m3lw2At4pLsMTGHvz6gr51N2rJ+ntZ1WqDPnn5WD1g7t6x/oWgwNK2UT79j7Z+tX4dcDwCKY7qbeovyR1tMN3ygriEwAgAiuuCCC9SxY0d7HKMpZkKI4uqlH+8T7vBXhxRYycwKhNMHmHbIDup1tUmEe/XedkY6AqhNzLjHdKW9UJFjA1uq99gXlZZOd1SUXpUGRjP2xW9K9uLK0aNH3bMBABWt/LuklqzVpZfb
Ссылка
Юлия Калиниченко
22.09.2023 17:17:26
Добрый день! в третий раз пишу комментарий ), скрин не прикладывается, представление диаграммы в Power Pivot.
Возможно укажете на ошибку, при построении сводной таблицы не удается совместить суммы из 2хтаблиц (Выписка и Остатки) по датам, таблица строит 2 отдельных столбца для каждой даты. Заранее спасибо.
Ссылка
Екатерина Шишкова
23.11.2023 14:06:53
Николай, огромное спасибо что делитесь такими крутыми задачами в Power Pivot, я поискала на ютубе и в сети подобные материалы, и ваш пример по решению (и выстраиванию связей самое главное) - самый исчерпывающий.

Будет круто если вы на своем портале расскажете нам и покажете побольше примеров задач с использованием Power Pivot. Мне инструмент кажется довольно перспективным, но многие о нем вообще не знают. То же самое и про сервис Power Bi.

Еще я полазила в надстройках, которые предлагает нам Excel, и нашла вот такие: Inquire, MC Power Map. Возможно, они также представляют интерес для аналитиков
:)
Ссылка
Екатерина Шишкова
23.11.2023 14:07:57
Николай, огромное спасибо что делитесь такими крутыми задачами в Power Pivot, я поискала на ютубе и в сети подобные материалы, и ваш пример по решению (и выстраиванию связей самое главное) - самый исчерпывающий.

Будет круто если вы на своем портале расскажете нам и покажете побольше примеров задач с использованием Power Pivot. Мне инструмент кажется довольно перспективным, но многие о нем вообще не знают. То же самое и про сервис Power Bi.

Еще я полазила в надстройках, которые предлагает нам Excel, и нашла вот такие: Inquire, MC Power Map. Возможно, они также представляют интерес для аналитиков :)
Ссылка
Наверх