Решение системы уравнений в Excel
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином "поведенческая экономика", т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется "Думай медленно - решай быстро" (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений - несознательной автоматической реакции - приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет "10 центов!" :) Но весьма скоро, я уверен, вы сообразите, что на самом деле всё не так примитивно и для получения ответа нужно решить простую систему уравнений (здесь b - это бита, а m - это мяч):
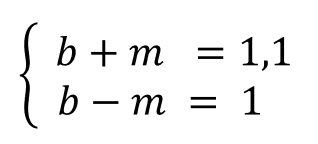
Конечно можно "тряхнуть стариной" и решить всё вручную на бумажке через подстановку переменных - как-то так:
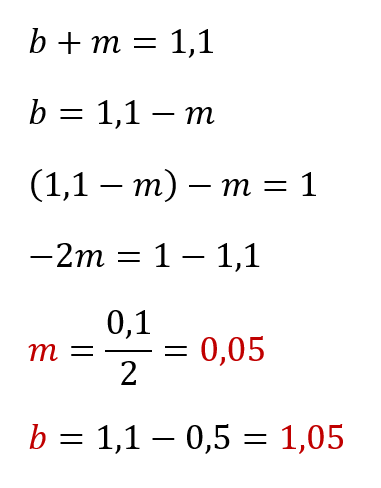
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel - универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо - прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае - размером 2х2, в общем случае - может быть и больше).
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
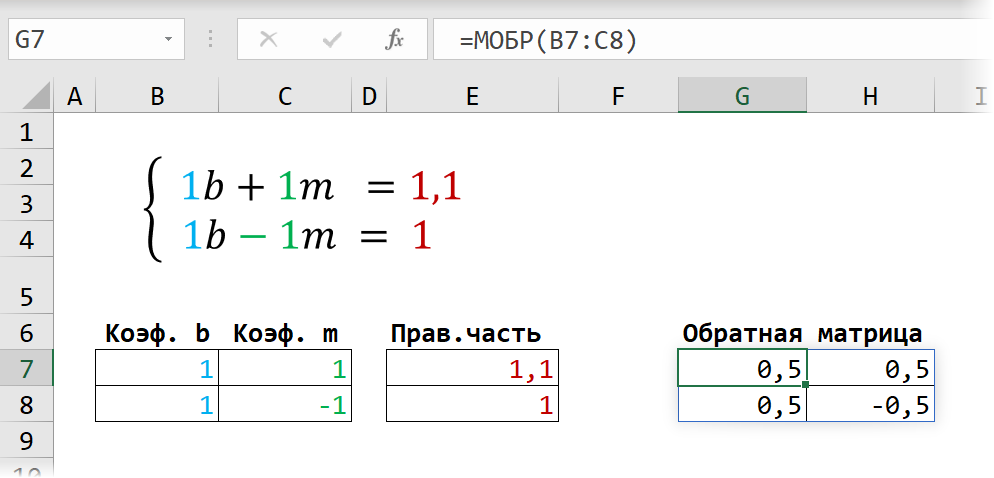
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) - сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов - G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
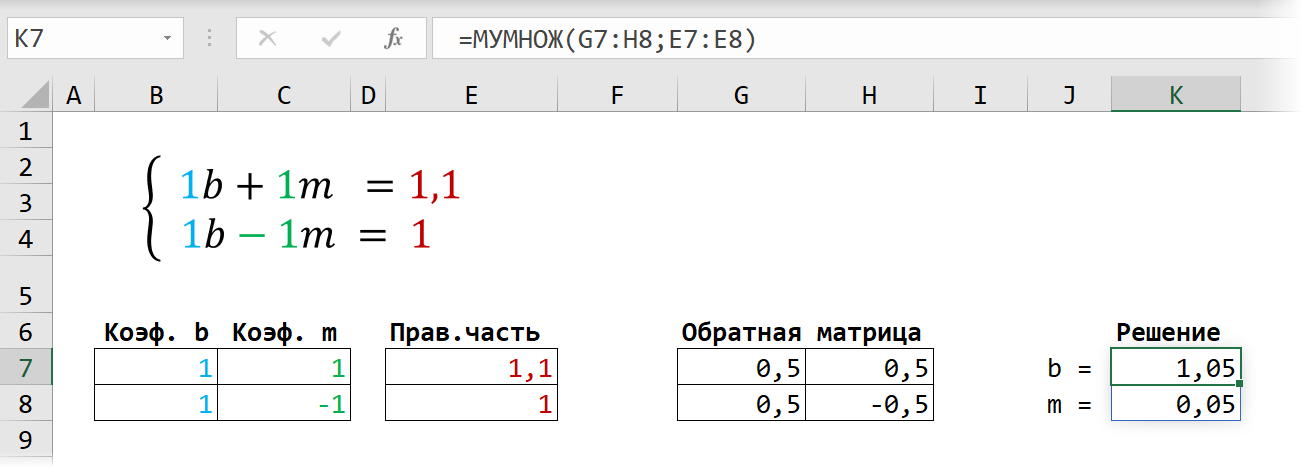
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
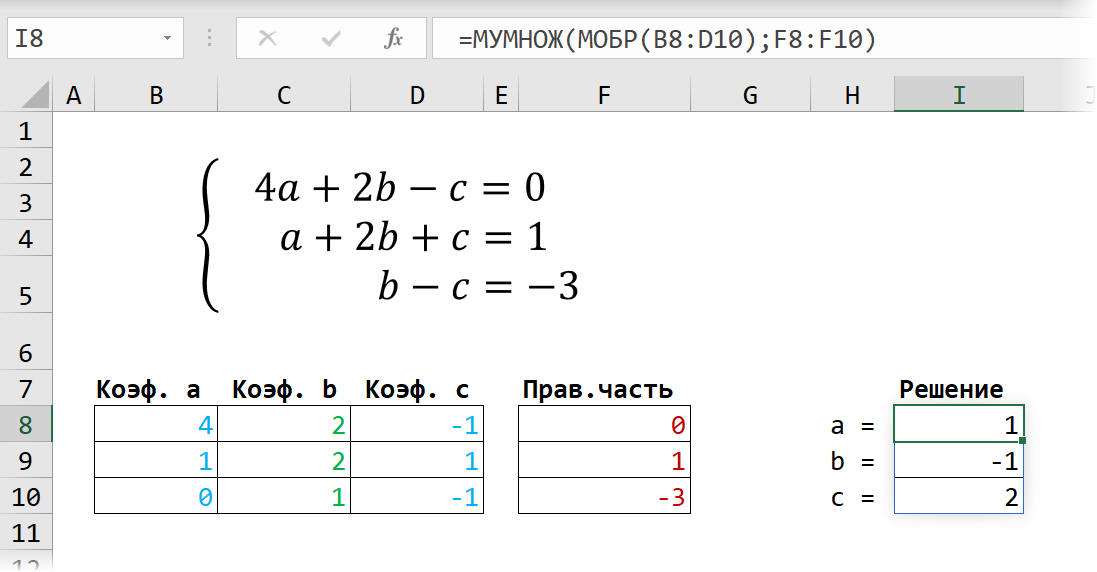
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем - через подбор.
Способ 2. Подбор надстройкой "Поиск решения" (Solver)
Принципиально другой способ решения подобных задач - это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл - Параметры - Надстройки - Перейти (File - Options - Add-ins - Go to) или на вкладке Разработчик - Надстройки (Developer - Add-ins).
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
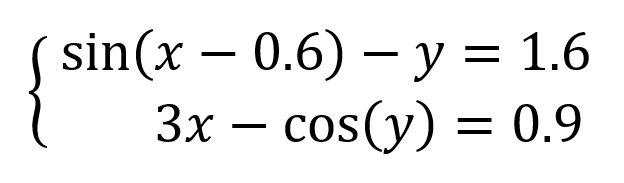
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы - роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, - для этого выделите диапазон C9:C10 и выберите команду Формулы - Создать из выделенного - Слева (Formulas - Create from selection - Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные - Поиск решения (Data - Solver) и вводим в появившемся диалоговом окне следующие параметры:
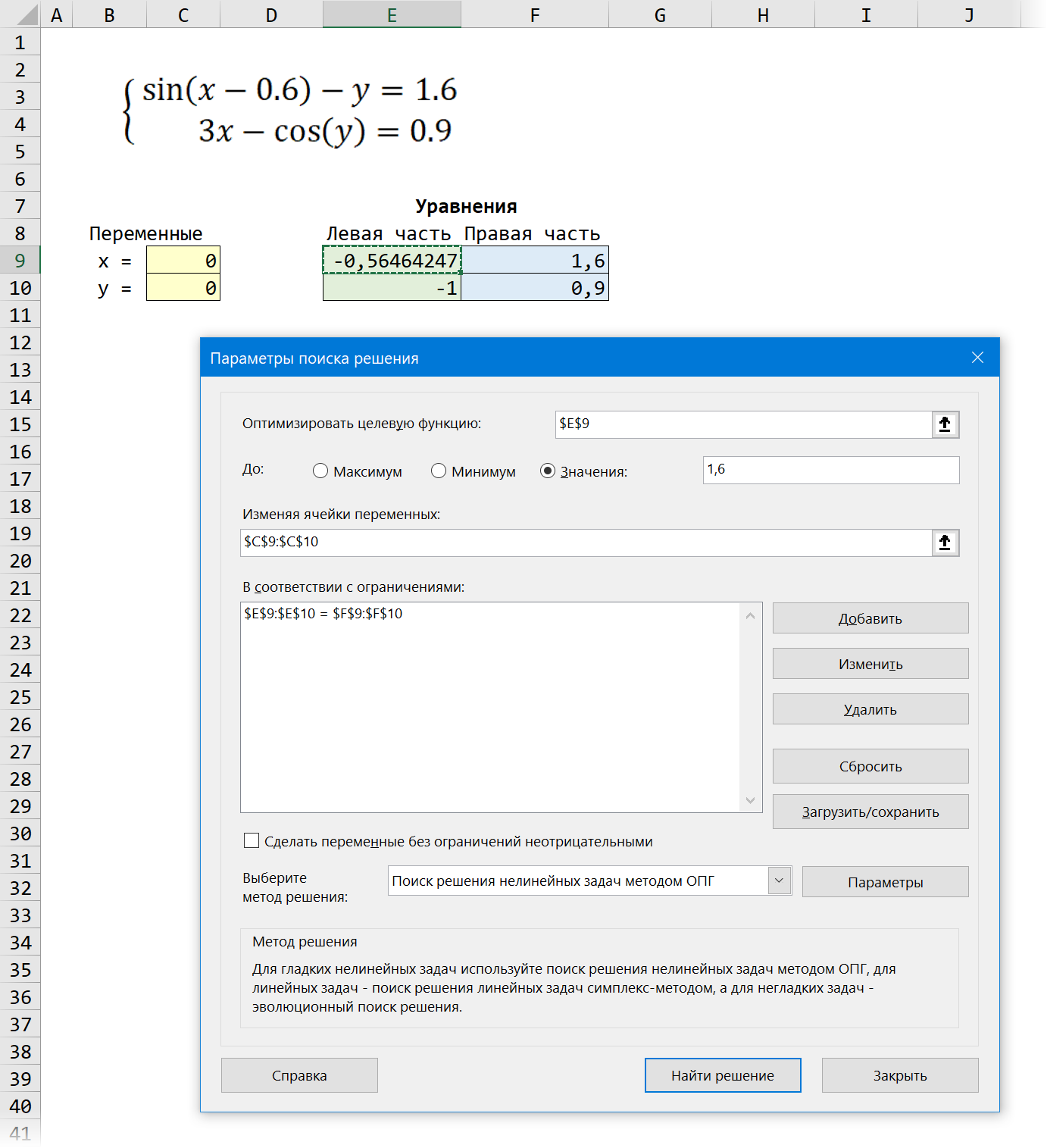
- Оптимизировать целевую функцию (Set target cell) - любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) - жёлтые ячейки с текущими значениями переменных, которыми мы "играем".
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару - это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
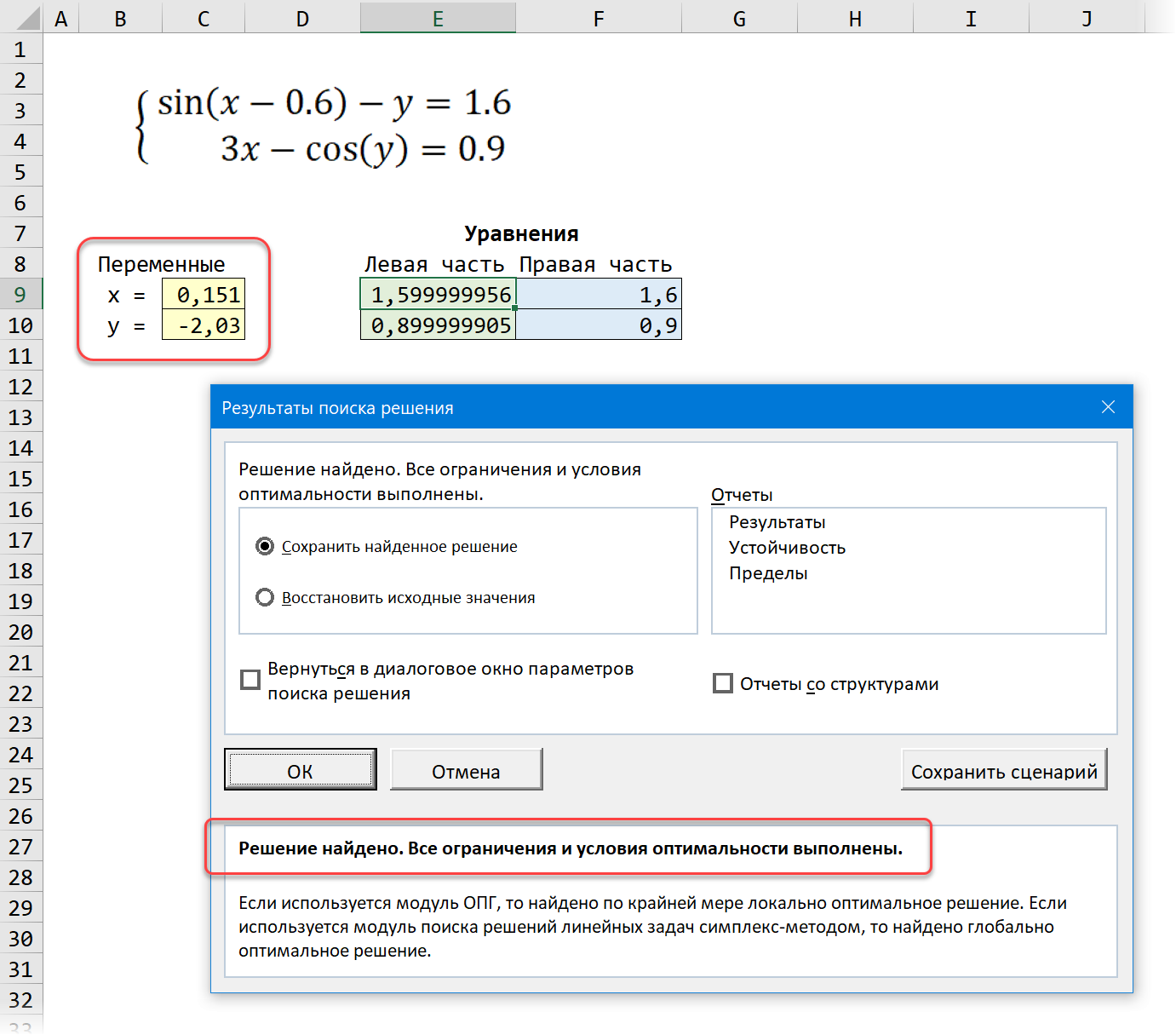
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).


