Расчет средневзвешенного значения в Excel
Основная идея
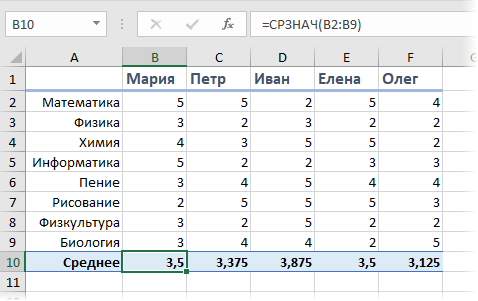
Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:
Свободное место, допустим, только одно, и наша задача - выбрать достойного.
Первое, что обычно приходит в голову - это рассчитать классический средний балл с помощью стандартной функции Excel СРЗНАЧ (AVERAGE).
На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется "Программирование", а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень. Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.
Средневзвешенное - это среднее с учетом различной ценности (веса, важности) каждого из элементов.
В бизнесе средневзвешенное часто используется в таких задачах, как:
- оценка портфеля акций, когда у каждой из них своя ценность/рисковость
- оценка прогресса по проекту, когда у задач не равный вес и важность
- оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности
- и т.д.
Расчет средневзвешенного формулами
Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:
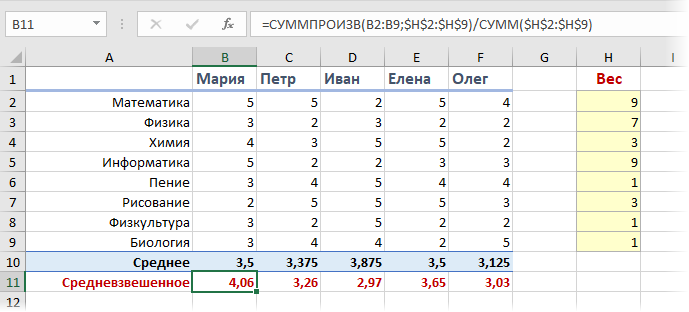
Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в двух указанных диапазонах - оценки абитурента и вес каждого предмета - а затем суммирует все полученные произведения. Потом полученная сумма делится на сумму всех баллов важности, чтобы усреднить результат. Вот и вся премудрость.
Так что берем Машу, а Иван пусть поступает в институт физкультуры ;)
Расчет средневзвешенного в сводной таблице
Поднимем ставки и усложним задачу. Допустим, что теперь нам нужно подсчитать средневзвешенное, но не в обычной, а в сводной таблице. Предположим, что у нас есть вот такая таблица с данными по продажам:
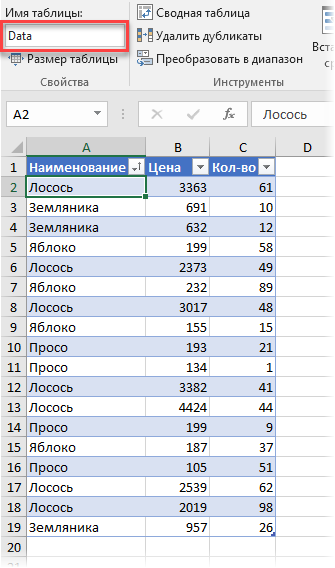
Обратите внимание, что я преобразовал ее в "умную" таблицу с помощью команды Главная - Форматировать как таблицу (Home - Format as Table) и дал ей на вкладке Конструктор (Design) имя Data.
Заметьте, что цена на один и тот же товар может различаться. Наша задача: рассчитать средневзвешенные цены для каждого товара. Следуя той же логике, что и в предыдущем пункте, например, для земляники, которая продавалась 3 раза, это должно быть:
=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33
То есть мы суммируем стоимости всех сделок (цена каждой сделки умножается на количество по сделке) и потом делим получившееся число на общее количество этого товара.
Правда, с реализацией этой нехитрой логики именно в сводной таблице нас ждет небольшой облом. Если вы работали со сводными раньше, то, наверное, помните, что можно легко переключить поле значений сводной в нужную нам функцию, щелкнув по нему правой кнопкой мыши и выбрав команду Итоги по (Summarize Values By):
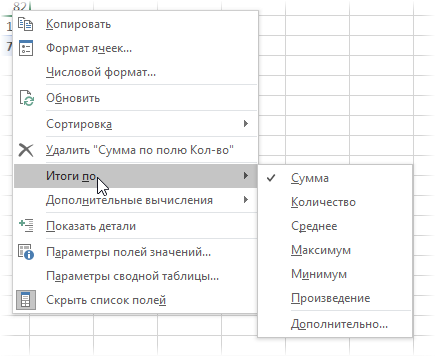
В этом списке есть среднее, но нет средневзвешенного :(
Можно частично решить проблему, если добавить в исходную таблицу вспомогательный столбец, где будет считаться стоимость каждой сделки:
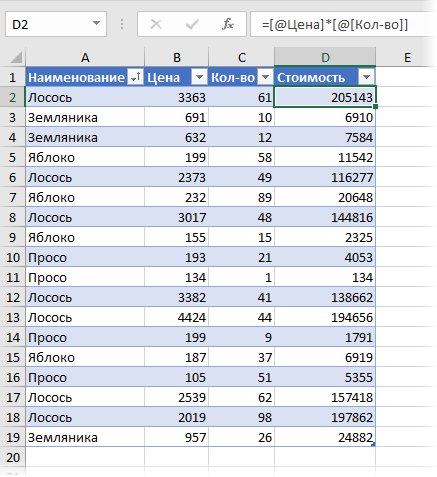
Теперь можно рядом закинуть в область значений стоимость и количество - и мы получим почти то, что требуется:
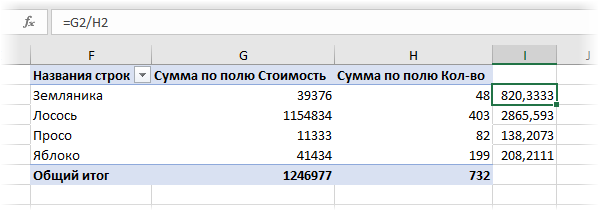
Останется поделить одно на другое, но сделать это, вроде бы, простое математическое действие внутри сводной не так просто. Придется либо добавлять в сводную вычисляемое поле (вкладка Анализ - Поля, элементы, наборы - Вычисляемое поле), либо считать обычной формулой в соседних ячейках или привлекать функцию ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GET.PIVOT.DATA), о которой я уже писал. А если завтра изменятся размеры сводной (ассортимент товаров), то все эти формулы придется вручную корректировать.
В общем, как-то все неудобно, трудоемко и нагоняет тоску. Да еще и дополнительный столбец в исходных данных нужно руками делать. Но красивое решение есть.
Расчет средневзвешенного в сводной таблице с помощью Power Pivot и языка DAX
Если у вас Excel 2013-2016, то в него встроен супермощный инструмент для анализа данных - надстройка Power Pivot, по сравнению с которой сводные таблицы с их возможностями - как счеты против калькулятора. Если у вас Excel 2010, то эту надстройку можно совершенно бесплатно скачать с сайта Microsoft и тоже себе установить. С помощью Power Pivot расчет средневзвешенного (и других невозможных в обычных сводных штук) очень сильно упрощается.
1. Для начала, загрузим нашу таблицу в Power Pivot. Это можно сделать на вкладке Power Pivot кнопкой Добавить в модель данных (Add to Data Model). Откроется окно Power Pivot и в нем появится наша таблица.
2. Затем щелкните мышью в строку формул и введите туда формулу для расчета средневзвешенного:
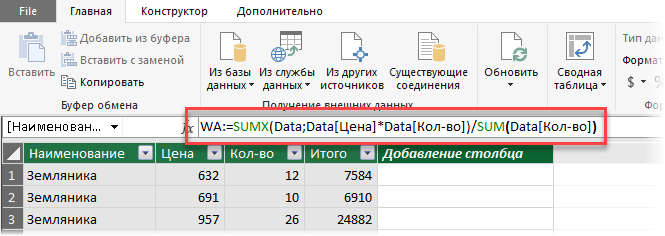
Несколько нюансов по формуле:
- В Power Pivot есть свой встроенный язык с набором функций, инструментов и определенным синтаксисом, который называется DAX. Так что можно сказать, что эта формула - на языке DAX.
- Здесь WA - это название вычисляемого поля (в Power Pivot они еще называются меры), которое вы придумываете сами (я называл WA, имея ввиду Weighted Average - "средневзвешенное" по-английски).
- Обратите внимание, что после WA идет не равно, как в обычном Excel, а двоеточие и равно.
- При вводе формулы будут выпадать подсказки - используйте их.
- После завершения ввода формулы нужно нажать Enter, как и в обычном Excel.
3. Теперь строим сводную. Для этого в окне Power Pivot выберите на вкладке Главная - Сводная таблица (Home - Pivot Table). Вы автоматически вернетесь в окно Excel и увидите привычный интерфейс построения сводной таблицы и список полей на панели справа. Осталось закинуть поле Наименование в область строк, а нашу созданную формулой меру WA в область значений - и задача решена:
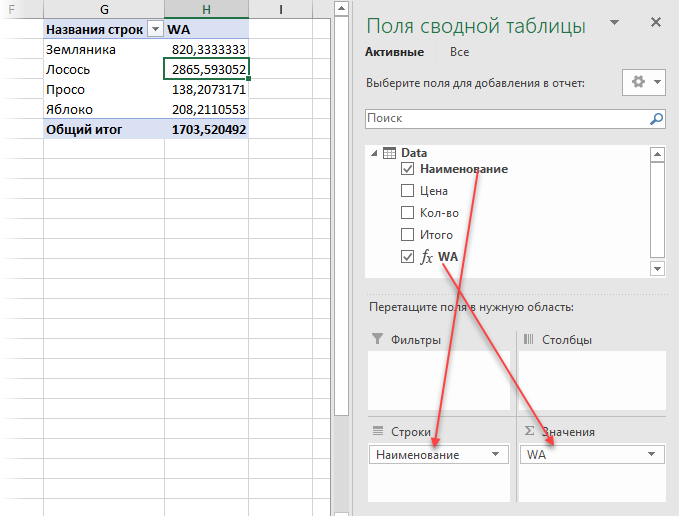
Вот так - красиво и изящно.
Общая мораль: если вы много и часто работаете со сводными таблицами и вам их возможности "тесноваты" - копайте в сторону Power Pivot и DAX - и будет вам счастье!
Ссылки по теме
- Что умеет функция СУММПРОИЗВ на самом деле
- Зачем нужна функция ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ
- Настройка вычислений в сводных таблицах

Стоимость/Количество
64xExcel 16.0.8431.2153
Присоединяюсь: Обычная сводная таблица эту задачу решает через вычисляемое поле:
Отличная статья! Не знал что такая вещь есть пока не посмотрел. Вот если бы Вам еще написать бы книгу по DAX или Power Query, думаю что такие книги были бы бесценными для русскоязычного читателя. Например "Готовые решения DAX - бери и пользуйся" ну аналогично Вашей книге по формулам.
касаемо Pivota
Можно вызвать редактор мер и сразу писать функцию, что очень удобно, подсвечивается синтаксис, вставка функций пишет описание всех функций на русском, можно поменять формат
*глюк экселя, если зайти через выбор полей, то не подсвечивается синтаксис
Умная таблица тоже разумеется при этом называется называется по-русски Дата.
Спасибо.
WA:=SUMX(Дата;Дата[Кол-во]*Дата[Цена])/sum(Дата[Кол-во]) Не работает
WA:=SUMX(Data;Data[Кол-во]*Data[Цена])/sum(Data [Кол-во]) Работает
WA:=SUMX('Дата';'Дата'[Кол-во]*'Дата'[Цена])/sum('Дата'[Кол-во])WA:= DIVIDE( SUMX( 'Дата'; 'Дата'[Кол-во]*'Дата'[Цена] ); SUM('Дата'[Кол-во]) )[IMG]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABDcAAAH1CAYAAADiVRXPAAAgAElEQVR4Aey9eZRVRbY3SHev9f3T/3avr9+r96rX12v1193rq3pVigo4ooyilpQiDqUik8yQE9agWM4+fZYDWqVWleVTEUdQyCQBEQEVQcQRyMw7nvnce3MiE3CEzF+/394n7j2ZMufoo3KtWOfmGSL23rFjR+xf7IgYUmhux0OPPIFVNethubleT45fQMYOJF83aJTfvGd7+e+V1Vc09AVfvZFn1isg67Qh7bYiaXlwAh+Bpylr+SIj18nBcXNIey1Iuc1w/TZYdoCsnYEfOrC88Hty7A3aBmseva4jXoispALSXgGWWxB5U+6eE8Jz87DtPNJ2ARm/GWmvCW6uCZZjw3Yt+EEOWSeE47TA8dqQdHJIeAHsII+MG8BxmF8I13XheK7kbblN+r7TJOX1lqxJh8mr1+V0ONtQlB35V9mJTnsqO9cJpb3b+SZk3FB03A8a4Xo5OJYLzwtEdpbfCH7HazLjit4fyUYY/nrzSlsUl9fhbFNvltdreRXln4PltEhyXF/0zHV9sQ1J30MiCGAX2tBgFZANWpB1m0SnWRe0zV4uD35n2y4cO4TnNSFlh8gEeaQCH+nAlTZCukWfpa5zg8729Lf+Z72cyJK6S7lQ3z3XhuPZSPs5pGgbwoLISZ6zzws8pBzajUa4bmNkD3q/3z1eHYvr/fF+85/pPSeywayvtB+Kraa95m/Wr+sUELgtyNjsgwtSrwnHgxvSrvuwnQB+UEDW8uQal40Z98Tvncq/+7t9HkvW0n69yM65eemD2IZpOx07AMcAebcNTpb1HootTLJP5/jV8Yr1b8phv2GSuTfQ175s32wnDtuCFyDjNyIdtCJh7YXltuv43vPlGcc+gWPDtx0ZT2WdRmlLKZF5z2wf7Wqxv/bYfnNodXdi1R8uBHbPAvbcgM6664C66+TaUX8dmDrrrgf2XC9X/h6ohN2/Queea9GRvA6HEteiY8+vgLob0bn7eqD+RnTWXwPUXQPsvgHYPQUddVNwsP56ud9ZP1l4GijatdwblOY91xdl3Fl3Azp3z8bKhy9Ei/OR9Iu0o6wbJvVZdLzY4/ZB/0fqvWS7JU+nRX0m9sG+j5znw7c8ZKxmZLy9sIMmZF31S3tMw+HGxidwL95G4zayz+nyQqkb2rNU0IoGt0nG5J7jwnZCHYeHjUjbnoxVXI5fbB+2n4P8tnrWdk+Uv7icjufbIX0NbnSvrLTlS+fQ/T6JPVHij4fBwf1OAVm3BbbPxsbfHnw/RDqdFRmRdioZFSmZCWUgnbbyCEI2TAcZxx50DkZfy7vXdSQyjuqUF9TJdjmo1YbPAY40ZK9ZwI2ETSedjrmHXC6QQQ55Zodtea1iNGk4U7YPy1cArwhucNAkDiLBDU0EU3pLZvE21etyOoKxVmCoK7hBfgQYckJx4tJOgGyYh+XnxGBmsh5yQR7ZrC3/p50cMi6fN4IAKI0teaGt6C3ZHC0fDo7i8ioOlo7A89Hy6u9nKn92MtQndbgURFPnLB3mkQ4aUZ8N4YZ7FaSzc2JDUmkHXr4ZDRlb9DgM8wJu0OlmfYjDJ+CG/3dw4zC6QOeIDi9tRxEMdRTEFHCDgwYCUK46SlkCd34Ar1BAfdIq2vj+1pl4eXG9j98/VX6zzdAGs75Yn+KwCbih/9uW1p0bNBdtFPtqJwiRth0BaglwmO+M7eCVtuxUkePx8DkQ/dMx6WIf7SuwwTrzCVAQ5A0ioCKTF3CDkxVWPifvyhhW+nIFkI9ZxmFsR39906ft2wtlvEqgh3Yw47fC8fcLyC6Oo+eLM0SgiOMlgkacKGJfpRMaPXeOtP1GDvPhwI26G4H6XxVTZ8OvwIT6G4C6G/TK3wOVGqZI2QcbrgMTGqYUgQ0kYrST1j0EO27CoYbofsO1EV8DSD8BGAJF9YYmghw3AXvm4I1HLho4cMNtkolITjBkPA+B4yLPvtpuRorAh2NAlp7rYE/bcryNxm1kT/M91vfss2jrCFYk2Cbz7QLWE4ykLeSEJAF6+Z0JdDKGdtALxS/1/eZ+7d/icjoWb3ze5+AGBcMK45VOiwE3WHj3ijxR4o+HwcH+Dh1nOryUCwdNAnJwkBU2IpX1RIkCvyCdLjteL3L8xKmhwziAHedAlN3bOsIGzsZ6WHCDnXHkYGecRgE32CnTGDDCJptJSQQCASga0QTBKK8ZllUQwEocdnbwErGhswoKbnCml1EbP/DIDbbhKHpAEHn+H/FEcCOwQ1hpnelK5xykQlsiAly3GaHXiNCPgJ0ocoPRAnQIGL0hEQUh5dP3nQ9tU1yv+H9/lNsbZejsY04GjiY6yPJ8BSY8dvAa8UUA1fFbxNZQpxlxRD1mpBFn3TgY9XxGHuTAqDHHb9I8CLbKLLZGBQmAEkVusO57g4feyiPen8Trs7fy754PZZ8KNPLLI2BE/WX0lBfqLL9XQMLRmY7AC5H3FKymDXEKzQp8eH2v393pjv/fH3KKlzfofkc6bOx/0Y4JaEUQUEFYzl4RBPG8vWLfrSBAxnOk3cT1zox1aL/i9wcd3/1gV7vzHJfHYNI72nuJJnRDBNHsZCqXQ4MXwPea4NkFiZbNOIxEoE4Q/A2KYP1g7i/6VM60c7YjgK3tMQqwoGMf2sDAQ9Z3xSHyvBYBDmWSw8lLZCDbGWXZXUdO9H/TXmlzmfh/i4nc2DMbqJ8CNFxfSgQMmAgqSOLvAUwEBRqm4FDDDUpPcgY690zBoeSNOJi4AR2JqXq/3vAwpXRvIOkulq3gjMiQIJLcnwrUze1XcMPoTVEfInCDkzscp3iOjxwjhbIEnVvhhM2ik+a7gbzG22jcRvY1TQLIM4o0DJCw6d+0RhGI9D8LAm6QniBoQZBvRzKbQ9L1JRKGPo9jq+/a13Sa/ONyMveOdu0XcIPG34Ro0nmhwHbVpb5n2E6U+KMx9kN4Jsplc+mCB4+OnJ8XZ4PAhu1yVoioWbMmgh9E2ZxAnJIGK4hmDXveQfwQZGVo7G0dkTogwOHqDCwHuSyL9znTIAMZO5BZOxrE4qxNJo2874kzSNCOg10rV0AiQ8e4HWm7WaI46Gh2ATc4ux6l3ozaIM1xw9jbcjLy734VB7cYFkiwgxFITRLOTYcvHzRLJJIXWkh7abiFvXCCNjQ02DIQMXJntAvRdMqyv2c8aZ+6yysuy+48D5b/u0QOuL4sfaK+sU7MTDQjwRzL14En64UAqRfAsl2xNw12E7L5fTp7aanNYeih6CZDjWVGWweOZvAo/Eeg1mCRBemI11n3+uwLOkXOgXb2Cm5o2G2pXkJ4AQf4toCgXPJDUJNL3BoYmSQDr4G13/0hp76Qfa/lWdRjjeAwg2PaMOkLbBdeoAAV+97QycPOaBvL5KJZfw4A8y3SN1AHaU+Y+tuO9ZpM+gj46O/2eTzyMPXFSSMu9yW4S9C3zvfB5XyO4yDPaCsuT5UBPaM1A1nel4jGDMdTzkC906ftm23H9yWKiaBu4BYQhm3IOnkBNgj+sT3J/xwXBE0CmnPZYzrDZz0Hx017Zd9Ee8z/m52PsPrhi4C6ORGAEQEDievRkbhRUhdwQ8AOA3r093UKkJoGpKfJkhMCG0jMwpf1M/F1eg4OJWZ25aHBgBsR6EGAZqDpJ6CRIB3XKy2JaUVwg3WhUdB9uyzFtC/Wv4nGo/3m0lqJtHZz8AmoWYxW0EgtTjywrzbfDtQ13kbjNrLP6SHow77NtmVMyLEhQQ4uvWe0i+1z6Z1O2DZkG5HyW2DnObnLibDIj+mjvuJwvMfldLjn3e/1ObhhZmB5pWPIDv/z3Qlsfm/798JyT5T47sz84P4n2mz7MmNK2TAMiB0BneodH2zAqJEjcMbZE/BJHVE0LkfRGQbOINAZ5AzgD47nHjaG3taRo4Ebsn8BQ7cYfURDyQEOQ1f9EPfcfjtGnHkGzhx+Hn429Cyc9vOf4IEHHkA63IcG/wDccJ/UpRhbrk2VREMaDaKjNYi9WX9xw9jbcjoinRGwYZbxmHD8rNuqkSmWhZxvocnO4v7bf49/GToMp587Bj8fcRFmLbxFEPSkxT1KuC8Hl1+5YiMYtWQA0SOW3UNdMvmyTrvLKy5L895gu1In2RExOsNEARlQg4O9wM2gNfsJHrxtEUaMOAdDzx6Nn51xNs4Ydi4mXvUr7EqFSPhfYY/TLoN1dmhc0sKoDu4xwPw1aQhnSYf1fwG2eqkOekO28TrrXp+9kf/h8hAZyNpV7ezZvs3eDI6XRc79FHfdtlDsxGnDxuCMs0bhtDNH4vRzRuMvy19XB3oAZdhfcjqc7AbDPQ5uzQBXbXW0LjyKQKOjy6imtOPD9300uSn8+1N/xGnDR+J/DL8QPx92AYYOPx+nDzsPa99+V+wZbZnsWcOldgNYt4Ot7IFon0eVQdR3CV1eqywRlj2H/LzsmxU0FRDaX2DXR5txwXkX4awRIzFs+Nk47ayzcc7oK7Fjlw9GdMb5Yl9y1DL7WR/6tH0TUHA9OI6FvJPCX//0JwwdMQ476jRyjXvIcWIn47iYMWM+7rj7IenjGcER5pqjyY2eOZdssyJvjqV9bbt0qN985CKgfi6QmA6kbvp+Sk4FTEpFv/v9ehOQmYLvGgi6TAVSM4DMDByqm4UX/vWn+M2U/wWHUrOVdtJKXniN8yP/DxT9RoYEaG4CkjdEtE0H6udJ5AbrguOGvtpzg3krsKXjFfa/ZqmSTDJQJ0L1k7g86q4ld2PypGuxJ+0iw+X9pzK44XI5OCdcLLQ4e/D8X/6Iy66bh4/SrbL/o++n8Zc//zvOOnssVm38CHWMSmebz2bBpeV+jmP8nrXfE/n+RG1Zn4MbNPZ0UnhlJ0BgY8v7H2Lj5q1dOgUyeaLEn4hgBuW7USgdkTAOogTo4H4Fro2//fkxzJ41DRdfdi3+9uJaJB1tiBI5EIXzp62eI9+DUi5HaTC9qSPsGOmUi4GMRW6IwZOBj4ahskHLOmtujpt14doO7l1yKyZf8Us1km6AzWvfxLnDhuLp5bXYkW6DFbRreH8UBWI6YeMwUu7mXm/VQXyQ1ZtyOhZ95IMz15RlOvBliQ43yWVHE7gpBNk6/GLUOEz+xbWoS3qoc3JIhc245ff34Pf3PSTAhtl3I9/UJiCon+u/9XzdwY3BNkA9kvyl8xZwg3vwxJLsARGiYKfwpbUNf1hyMy6fdB0+STUhm2sFwdEZM+fgrBEXYeX6T5HOdyLpt2i4oe/JZrkEoWXgHttkNw5u0Kn/O7hRcoxLdURASMEfz82gxfkQD95ZhksnT8PHmQPIeO1IMbzTKcgyNtqD0rf9N1AwZfannTBlDpartJ9orw3SRDsmSSLrdMkgI8m4BEHsv51Gq/MZnn/qIfxi8lTsTLWCkU8EM5hYl7RjvJr/Bwuvg4GOgeqfjsY799bgmEqiDYNWmdVlZJvnOUin6nD3nYtx7rlnYN36d9TGRlFxjz35Ii6/aqZEYRm+2G+YdLQy+/NZX7dvys/3LLRYX+CFPz+Osy66Ah/UtSBp0xHizHgaSSuFmdMX4r77lmp0Mje7jvaT66ksimOoCNxgfkVwIzEPSHYFNzrTN4EJBDIGOAkt1k04mL4ByETARf2N6EiV4c/3nIPFU/43fJdeGAEHfD4zopn03wikb4zAhIHnBemp6ExF4EZ6BtAwHysevUjqIg5uSH2zrqJJvp7Xv/pApXG17j3GMbsBPbjvlex/Z/u4//Y7MenyK7EraSNhNrI/ir/RU/qO5/t4GzW25Hi+64132E/5noO92R148a9/wIVX3Iyd9rcSbbq+ZiV+fuY5ePr5VagP9iGTa5ftEbjEh+NDAvi9QcPx5hGX0/F80+fghggh6wmQsbs+LREbb296XwCO7jOzJ0r88TA4qN/hjF+oG4lmMpbs48BZ7kw2gek3z8Nfn3sRd9x+J2bdPE9mFTJBG7K5ZnDH7sHWifaXnHtTR9gxmogDGlsZnEZrrdU4cmZGNw0jwkkeue8Jw1TvX3Ibrr7yCnyeduEUmpBL7MTsG6/ClLK78FkeSPs0BHqCQskpNDPt0QkKvRCWGZd73DD2ppziZXT/LY4c16LbXIqSk5M1UqErs9fcdXmv+wWee+LfcO75l2HnLjrQB+BwV3XXQcp3BDk2jgAdA4lgitard7cP3cvurf/ZluLy4v+9lXdf5kNwgfthMLEcXe6kG9WyPgpWFvszH+CB2+ZhwnVzsc36Fnu4NMV3kLN24+apN2D6vDvwufMdEl6L5GMHDlKZNAguySa50Qy2aSsCBEbAxqkObpTApYIAQ5ylZNQdbYosybKzaE1vxwO/r8SFk+fhfasDCW9v0eb7+YEFNqgzcb3vS10djHkbcIPRTjoA17D2UjvSdcd8zsGxayWx392OV595EGMvvxGfOQdhFb5Eg5WTyCe5Rqc+GZCjNOjuf+BqsMl8IPqno8uAe2PpSThst4zMIY2cXGpxPsdLzz6Bn424CNXv7ULKaxVAkqA8Z3ydLJco6R46cb6OXl7/60Bft2/uRcMx6z57B1548gH89PyJ2FK3H2lvvy6rzqeQdpKYMW0R7r3rcTk9SvYp4qSSOXWrB87l4cCNRvcjiRoAwQ062pmpoPPNa0dWEzJcCsJn0wYskZaD2evxXeZXgEX6pkl0Rkfqt3jy3nFYNOW/4ZvMLXqftJokNBMQuSHia+B46ExNj+Q3FR2pGxQ4Ip0N8/H6IxcWwQ2xqaaeexXc0DYl0ZIyUWA2Vie4wU39eQoW7XOTTDbee9sSXDdpMurtAPVcdjvAkwu0F/E22t+2hPUSOFm0Wtvx3J//FRdfNxcfZfbDTmZxxYTxmLroN/g02CdLlxPpQJaeuRyfczP12MRAf9i9uJyOp7w+BzdYWQQ4CGy8s+UDidjY9O42EODo7kScKPHHw+Bgf4cOAndeD4IcfDuDvL0HH+94D+ePn4SddS421KzEmPOHY+duB/X+lzLDynVk5ItrQAc7f71NX2/qiHHY6IzEwQ0ZzAryyxmdQJwRhlIS6GA9uek07rv1t7h20i9RZ/ng0YAt1m7Muela/OaBp/EpZ8LdFj15IjrKl3JQZ6g0sysAijH4vXCNG8belNOR6pD8yOCdDnMM3DBHh4ZOFk2JrZg09hzc9eCz2OX9x/5e1r5optOB5dsy+8/lKMYJ4Ewp+ZB9THpBJkeiPX7/hw5uyLpnCf0kWFfQurCbkBfn+n08dHcVLrhyHj5wgETQDtdJo8X+GJtrX8fQcyZixdsJNPhtcqJN2snIOkwCS3FwQ04NMlFOEbhhQJW4LAfyd3/rv9gMszeDxz1MuI8MT0QiuFEQcOlL+yM8sGQRRl87H+9bh5AK2oszSv09ODhc3fSHnThcuYPhnhmgUY+7gxu0Z7I/ihzpGyJleyiEFvZn38OrT9+PS6+ZjQ8z36DObSseES7HLEdLufQ0CLOsa+BBrEEh79h4ZTDonfZdLbC8ZjnNg+HZ7OM9N4u9mW1YMOUKTFl4Jz52O5BwmsVRSoWNEnElm7uLPSwBFrQ/cRs0GGTe53L2cwi9NPZb27D8T/fjjNGT8E5dG5LuXj0iNkgi6SQwY3o57r7nT0jxUIFQZWY20++JnI4KbqTmA5mZQHaapE5rGjrsaeiwpqMzOzN6xt/TgewAXEmPOwUH7RuUxjTpnIXvEr/Bk/96Oebf9N/xdfa3QivpjdOM7E3QNG3g6BeZka7pgE2QY0ok65uB5AKsfGwUCDTRtvYbuOG0RGUpuMGIeEZu8NhhjvPuX3I7rp34S3yRstHAfd7+Dm4gdC20Wjuw/JmHcOnkm7Az0YzZMxfilxMn4+NsHrvz+5H0mvU4WB69bOtJKuw/e9J2T/TbE7VlPQY3ZIDADZbIqK9M88owTjqE/P3Jrnps3vohNr77Ad55bxve3rJVfvOdOIMnSnz82x/sbz8vAycCHJ6dwl7rUzz/9KO4+No5+DjTgiD1OX457jz8+aW1+DQ4JDOsjCLgTtPc2OoHy/dJOq69qSPHA24wsoazE9Rl/ubmr4Fl4f7bfodfXTkRu5N1sAsh3lq1GhecPRIrN32IXeEBCf+3LM6m09jqbuEy0x2Fy/VFvcUHVr0ppyPRaoANhvSazos8MtEZztsZJN5/A5eefxqeXvYWPg8h4W1JOhOOIxtgCs0mPNDXk1LYCRHc6A5+HomOnt7/oYIb5Juyp5PNmUeGC9KpJsBB4MzzUmi1P8B9v1+Ei39Vie0EN+w25D0bzdZOfLrtbYy4cDL+uGwLdtvN4AaJdujKMdMqe+Yd5c8jkWODeeMY9lT2vfl9f+s/aTd6T/lzpoinJiWlX2sCwb192Q/w6J3zccnk6/BRmqHaurY/kTuA3X677JnSmzI40bz6w06cKE399b7qcMle0WZJfToEa2m3m2SZXcK3YYchQieFA8kP8drTf8CEyTOww/5aQEEuMSKwwaucphU0wewjZEDb/uJpMJczEO3zaPJg3XDpHSMH2Xa5gTvHVpxkSn24BhPOPQ1Pv/A2dnsQ0DL0krIRMx2iBrcZaW6eOQico6Px2Jftm+0nE3AZdQYHMh/h1acewtBzL8EHDc1IB60i06yXQdq1ccP0ctz1wF9AcIgnLsjxsLH+5Gg8HO0Zx3DSV0XjDv5u8nbKkgikFwHZm9XxtmYA1gx0OJpg3QxNM9Bp67N+vzrTcdCdioPudHRkSM9cofe7zK/x+P2XYP60/xtf278T+jrtm4t0CpAwGOi3KbuILoIbzowI5JgJyn7Fo6OPCG70ll004FYxcqMbuEGwkpPBPBGOY6L7bluC66+cJOBGMtdyyoMbPOXIdSxZbvniU/fj6quuwYLFd2HoyInYuseXyXTKVuykb07ea5E219/+54nash6DG3T6uGGLGDpuvhhoKGfS8uT+x1/U4b3tOwXQIKhhwA3+5jdxw3WixMe//SH+Fv4JCDESw+fJEjZaUtuwaOpk/PaePyERfo0w/QXmTrsaV8+9FTv9TtmwUnf25nGOXcGhH6IMTpTm3tSRI4EbUi9R5AaNoywdYhiWrWe1NwUB7vntYlww/HScde5w/OzMoTj7jDMw8RdXYrfbgl1BO+oyOXihDpDpIKox13WARLLJd28PjPp78Cg8RbxRloYv8sb/CW5kPlyFCef9FE8uW4vPAiBV2Cdr2Lkpq8Wjjr28rFNn9AYdA0Z5megNLlE5Uf04mfdJQ1yvZLB0kuDbyZR/8t+w/X8f3KCDJgCTn0Crux333r4Qo66ciw+SB5F29yG0benMdu/cgjPPuwJPvfQ+Urn9sokej+/Luo7Uy+EjN9Rms41IhNMgklN/6z/rTfXeAD+hABvJaP8Fghtt6ffx0JKb8fPh5+Bfzr0YPzvtPAwddhGmLLodX/htfwc3Blh/4mCsbHonofIG3Cgg5XvIhE4EbmTwdeYTvPrUw/jpOePxfw6/FP9y9licPuJCXDbpelmeQhvGJSlevlU2T+ytQfzJ24iuY6yBzGcg2uex+OXYlYBGynIl6sINmhE4NpJbV2PiRSPw1LJ38IUHuL6Hu39fhbPPPls2Zf7JiItw/ZyKQeEcHY3HeL92tPdO5pn0ASFtYAbtyZ147cmHcdo54/B/nTkWPxt+AU478wz87IyfY+iIETh9xMVYct+Tss+BnLhg+cixr+9h++f30l/HwI2C95E41siUAdasyOmeCTgzccjTBIf3mfT+QFw73Zn4zpmGg+4MwJ8PZOcKvR3urXjigUuwcMZ/x9fOreh0Z0kSGvmu0Eza5wwoD6S/C20EN5is2UCmAiuWjimBG1Ffqcu9CSj3zvjX6E8R3ChOtGnkBveEYfvmshTuaXj3727FtVdehT1Z7+/LUiIfJAw8tFkf4+Un78c5w4bj58NHScTa7uBLpINmkR/BjbTdJFGKjIKhvYiP90/GfpzoNydqy3oMblBxZLOtqJMw0Rop28cX9Slsen97EdgwkRu8MvHbOIMnSnz82x/ib+kcnEDCpogsuk4GW978K8ae9f/gnc0fI+W0g7MFf33mSfyPkVfhlS0pcZo5SxgwfN/yusjvhyiDE6W5N3WEhlFno0vLUnQwWjodgstSjIFkJ8rNxrgs5YHbf4erL78Me5JZAaYCZw/mzZ4qiOf7u5vgN36DTCaQGR8adD3Voilyhgy40bsDz/4ePJoOileVJfkp7V3C8N7MttW45Jyf4Mnl6/GRfVBmrh3LFZma700INzcoIrjBE1O4LEKOR+7h4Od49OuHC26onnLWkYmdjc448/SUgkRutLnbcC/33Li2DNtTh5Dx9usRxskP8cmOd3DB+Gvx+tt7UO/tlb18vBzPLufRsTyWV/ORyJAukRu6tOrv4AYHaDrzT9mzDRhnlr8J7u13uCxlAcZPno4d2a+QdrlhLk+pySOR00mB49HRvnqnN+1pX9HYl/nSBtE+67IrjdwQfZdlKdwYNC/RG2nXldOHvsx+gheW/ismXDcH2+yvpN3QbrHeGa3hcjbQYRSrghx9SfsPLe/+7p+OKR/2y24WVqAgOyN1mMJMFulttRgz/Od44sVN+CiEbj5oZyRiluD7nff+K2bNXzTox1992b7ZdrikK/BtHMh+hleffBRDL7gMW+oKcBr3Sz/i5V00ZNOYNrMKS+55Aim/KYr2yMHO6lGTx6yno4wBaGfj4AZpIrix8rExgFUOOHMB92ZN3s3o8DXBmw1NNwPewCWCLZ3BLCCcI1EQsOfj6+zv8Pi9o7Fw+n/DV95tOOTP/T6N7mxA0sDRrnKLy3Gmypkyz1YWwQ3aV9YTE39rn8m+svfGvwQ3aIM52aPRlApucPzODaFZFqPd7/jd7bh20jXYlfaQCJsHBTgZb6NxG9mTdnE838pYJWiBlU2jPb0Nrzx5NyZefYPsMXTO+Zfj3gf+iPqwBclCK2y/Db7fJsdlc7JXAKNerL/joTcup+N5v8fgBpedENCg8jAZpnc1pCVKw57B0DEAACAASURBVAAZjNgwv831VAc3WEEiAz8nZzGzk3jw9gpccOZPMJxHBg4diTPPOg2nnXU6/t/h4/DbB/8GO1c6hYNrFo+nkv8zvXOiCn4s3tUpMWCDGkjqsRpj3fCVnScHrjQ8Aiw5Nu6/PdpzI6OhrIH1KT7a9jaGjb4Kjz63QTbO5J4oPFqTGw3yuE4mky/pYjnHou9EnscNY2/L6Uh0mHav4dzsXEoyJLiRq3sXkyecjyUPPYvd+f9YJmo3I/RzSGSy4jjo93q6AJ0CDhwJcBypvL643x3cYBlxWfZFmb2SZ3SiD8EIM2AguKEAB0+qyaA5+z4euKsMo6+cje3pDtnoLfB8FOzPsbH2dZx+7nh8sKcRqWCvbhDFPWa45M3jEYesB40OE+AkCtvXOu59/e2pTOJ11h/6b4ANXkk72wBlwzZO0JTHI37pfYy7fzcPY6+eh+1Wp240LJtC+7L2vLdtwInKsD/kdKI09ef7OiDW+iotu9I6ZD0yAtVtbJEBcuhl0Z7+EC//+RGMv2Y2Psh+haTfpssafN09nkscmBoynkRv9Ccvg72s/m6fx5QH260sOfIFkLLdVjhWIwq2g/yeD3DV+AswZeHd2OkDDVxm4esR2TwG8fd33IVZ8+aLs3bMco7inPf1t33Zvmm7CG7YVgpf2V/gxScewpkXXYHNdU1o4LIuN0TGTcEJbUydugD3PfCUgBsJL5D94sJAJ3t6IgO20cOBG4wagF0BuPMAf5Ykgggdkuag058HeHw2R8EFf9bAXHNzgNwcfGtPFeAF+QocdG/H0w+OQ/mMH+Nr/1YcJPAR0WmuytPNRb74v4Ak/XklTf68Im3wCbTMUrnaVQJuEGgy4IbUcx+AG2YMqbZcj4Kl7glonaNd9uBxqwTLx3133o+Jl1+FOplg4OSCjm96ooM9/TbeRuM2sqf5Hut78p6QSTAHB7IfYsVfH8K4q26S0x6f+esynHfOSKzatB2fclm90wYrk0eY4ybMgfSLBPCPVUZvPo/L6Xjy7TG4YZahMFKDv5k+3d3QBcggsNE9goMAh0R5xAz/iRJ/PAwO9ne44U2ukIeTTcBK1+PSSybirnsfRkM6kHOE6UyHYYhbb7sdE6+6FnV2sw6ofF33NNj56236eltHjgVuZHlMnMPopCZxuhktE7oO7lnya1wzSY+Cpc63eAl89uEW2VBr6fJ3wKNQOVh2XVdmMEqRG7p5nQEBelM+ccPY23I6Ep3Gqc663EugVWa+DN+Bm0CT9wnuXFKBcb+ci0/TncgGX8omrQxlDUJHlvyY9elcmsKoDYIbqawn0RtHKrc37/9QwQ3jRFPeZnNKhtYHFk+vUXCj0duGO+9eiAsnz8HH3PPEa5dzypsyu7Fg2vWYW3Yb6jzdMIqdFSNmCMoR3NATH0pRTCzPOPA6oOhdcK6nddrv+m/2z+GATY7iZaQLlwnlBNTMu3VoTW7CQ3eUYcJ15djU8LWclsLZpITjyyZnfwc3BlKHOLAtLesiSFjUQYmGCuU0DR5fTXvtO2m02R9i2V8ewugrb8YO95D2xdFx99Q/grO0XYw647WYX2ycc6re6/f2eSyZ84h3X2d2U4xSC9rh2HnkrAz2up/jhT//G84aPhrVGz6Dnd8vy478fDu4dOW3d96NGfMX9voERW/rRl+PA2i/eBTsAecLLH/6MZxGcKOhDSl7PzxuFO4nkXYbMG3KbNx3z1I4+TYko6Wolt3zPePi4AbBJ9KTd3eIYw2nUpd7BLMBpnA2OsO5khDMhybzf/9fEcxVQCM3G525mUAj6ZyL77wleOreUaia/mN8E/4GB/Oz0BkqvUJ/jpEeM6OkPPE7PuvvK+mSckPKd5bKmUts7Cq8/thoiaLpS3DDjEPMle2HOmHaUZp7bjiu7JXnOSHuWHIfrrpqCnanPNFDfmfeHahrvI3GbWRf00PeOW50vSz2WZ9j2R8fxrhr5mKncwBWNomZN10ne+h8nNiLtNUqcuWyZZ5ySDo9T8c6fU2nyT8uJ3PvaNcegxtFpYo2E/1sT0KAjPXvvFsENAhkmL02zG/+//fIjZweNWplEFr12LhuDU4fPha1mz6TzckIfHB/jXQyg01v1eDcc4Zh5VsfYLezDxm/VULHj1a5/xmfnaiCH1UGMvOtCK/qsQltMzN3ochfDY5ucCnghh/gvttvxRW/uAT1aVuQ4ZyVxuwZ0zHuqmn4ONsKK6Qx0EgPGncFN3TjRwJWAm5EA+uj0hgz1Md6L24Ye1VOR6Ih2peEAAejUojuMmpANrV0XbheCr73OSy7AaPGXovLr5yP3ckQiayDfD6P3/7217jr3gcFOKIjTXAj38SwfV+OIj0Wv731vDu4ITNBR+J5EN1nJ242EOVGlkx6jzPResRXwfsQt98xD2Mnz8T7DW1I+q2wHQ8LZ0zH+cOH48PPknKCSsLmbuKN0mFxSQr1U5cLhdExp1FoabQngYJzAz8wiOtAv+s/dcEAHN3ADUZrhW499jsf4sHbyzDmipn4xO1AJtwrM8C0Bxm/ecBnjvrFTgyiNhPXF9HxYhgzl3UpuCEDXom48wXccMN26WsZidZmf4YX/vIoxkyeje3Zr1Bv6T5BxmbQdvE3QUICHV3LG1ztpb9pG5D2eQzdY38ugG5hn5wIwJMAuOdGztkFP/sF5syYi7OHj0Ht+nelfxLb6Dfiljvvx9T5FQPefo9Vh33evv08fM9BU/IzLHv6jzjtwl9i8+5mWf7o2CGc0ELaqsPsmfPxwP1LUZ/NIxO2aLTTMermWLzxedGRlSgcBTdyXgRuuFVAsECWfDA6gqkjP08Scry/AMjNG7gUzgPyCzTiomU2vgun4xsukcnfgWfuPx+3TP+v+DZ/Cw4VZkPozS1AR5488H+TyNfA8dAhNLF80kGAYw4QLgScxf0Obhh9UJ2IIojDvOwhFjgucv8RzTFlyhzcPHdxtAH04Ig+jbfRuI08Hv3vyTvq84Sw7BRaM7uw/JmnpF/blt6LXN6Fm92DsRMmY9qc25Cx9yLlNkq0aSYXymEWtsVl9/3Xp8XldDx89xjcMMtQeCWwQfBiw+b35XQUcyqKufJZHNyQQURMOCdK/PEwONjfIbLo+y4avRTuXrIEl0++GZ+lol18PR++1wQv68NL78all4zFbQ8sxZ7gADLeXjh+/yJng0GWvaojxjGRULmcrL8rhrZJaDlRTbP0R0POJbzNtnHP72/F2cNOx7ARwzF02Nk4a9i5mHjlddiTzSEtDgzD+k2UBvPmpqI5eI4LGlrOGAog0IthcXHD2KtyirXRLjog8tNlNyI3pxWutQ+upbvIpwOeM56F7aTlhJlZU6fjzKFnYdjZF+D0sy7ArIW3FHer5/cEOOgccLBJXnjtUt6R6Ojh/R8suCFRGlyG0oRkGKIhx+UpETDBcEPXRqP1Ef7t7jKcedbZOH3EKJx2xgjR15lzKsTR5o7/DTzKt7BXAA0O7un00bYwL9Yhj5oVJ56DSYc2R2e7u9vv/qiro5XR7/ovS8ui8FdHw2FJnyxT4Wk1bhZN2T248zflOG3EaPzk7HH4l6HDcNpZI3Da2aNw5wNPDLhz1C92ooft82h13tNnuj6bThJtdRzc0H1sEmlH+1mpTxvN2RSe/+tfMZqnpTjtsPLtMtCjk8wNvmmzmBh91l/2q6cy6K/vB6J9Ho03DswlyjDqaxJZ9leNCBtbkM5mZFyWTWewacPbOOv0oRg+7EwMG3Ymfn7mcFxy9Sx8muSafUZr9d8A/0TL6sv2Lf2DH4qs9gc+nv/TUzjr/Euw9QvuqUUQPdBjxa0srp8yA/f/2xNIuc06cefle+W0v6JzFQM3QvdDrHx8LOAtVkc7PxeIUmdhPpiQXwjkFgJ5/h6gJOVX4JA7B2iOUksVvvN/jRcfHYbfTP8v+K6wGIca4/TPVfpz8wGmgaI9KreTcmxcoPItzAEKBDoWAe4teK2fIzfYNkqR2LqJf8LxkHFsTBg9FkN/ehrOu+ASfFLnCLjBgxwGwxgm3kbjNvJE2/rJvM/9BHO5AGF2F5758+O4ePLN2OV/hYaMI6eovFVTi7OGno1nXlwtJx3udvQobE5OEgSmvE+m3JP5Ji6n4/l+SKGlDQ898gSqqzfobF1kqGk04imeGRXCJO65wd+f705gy/sfFo953bh5K5jeeY9HwG7HO1s+KG4sun7L+wJydFWsAlbVkAaz6UxXVK2ktOpkmpnDIh3RLLzQHK19NjTrYFMH6V3LNMhvKU/zTdFoyppz8/wwnVjkIBfpiN43gyaTH68mpJu/9X2u+czBDwN42SRC15PZ77S3XxsdQ2OtHHwnj9DJwLHTErGR8PYi67bIxnRaRzrANg5IvMzuv4UukU83Xoyj362j7i4vQ7vJ1+iI+T9+jT/rLp/ie0coV2fVjNxLV+qp4cHkb66aZ+ld+f8w+Zv3VaeMvpmNjqL18zH9F4Pj6yke3HE54PFnVlrCMR3Hks0x0zaP32wVZ50RCHSYmVgWeYmDGzyyk2HscXCjRJO+r/pteNG6MjLUpSCxOiePsn+LtkW+VzIEJholqu9u8lD6uuffte2ZujLll+qG7cfXfUXIp9Mi4IZj7xPeeKY9OxDuO5Jz0withOg4w1GzwV4knGaRgwFImT+X+FDe35v1NHRHvBqaSvQbWfGq/MRlerT3WE/VNeuL9o//Sx6mzKgOyXeXdt2NFn5TKieSd0RLkSY6wd3umWfxMkuyNvkY/uLRAoXikZVyBGmoy1O0fppkf5iCsxv57BfwrCx8L4+s5cjx3JR9g98me21wkzeCS7KJqMPoIjpmZv+kbu0iBm50oftoPB3Hs3hdGf0yQKMpx8jE6H/pShlRb0r1tmrNulhURUwfTN/QpW6NjE/8Kn2LAUK5kWS0ppg0M0KLx+76tiUzlUkeuxbqMb08KjERnTRk+BuIa8lOnDjvQm+sDZg65H1TV+aeuR6JR/O+ea7/U/cMXar/1InivVjZ+p1pIyUbYPL7/lXfLbbnbvogQAePBw0LuowuyGt7yroI7BANYTt2h22ytIhOHIEN9ie0HQQ2CNJ2tWHdaetKo9FlQ+fh5WFkceSryDkC2sgb81N5mfKP8G03/g0dpcikI3x3xLbdlT+hwykNhI+od0egw+iPuRbpO4HyD/eNHEnKvjPrIchzb5UQySiKkO97nicgcWA5Mpj3A1vA3oRzAAnnKxmHHS7fE753BL6NLSzld/R67C6frnI2336/D+J3powu+hLRFbfFcYcmRdAv14ggbSHgBvccAwVtYouFFgJ93MMsbJRlPU7QphMabCeyt1lJJ0z55mp4idNmnplr8Rnp9BWYzzkfYeXjo4GgSh1tOtySFqCzURMKi6BpgTrnhZO80rFnipUh/5v73a8sR8qaF4EC5UChAp2FOTjUNAeHCmXoKPwGnYU70Fm4HR2NFehoYhlzJXU2LgJTkXaTXzxPoceUY+jr9r+hS76LPTvh/xeV+BcaCbiUAd6vBdzIex+X7DV1LNY/mjrsybW7nYz7idJXhHnZbJ2+VV6ONG2Wfpcnfqiel/S+J3T05Nt4G+1vcIP+jOM4CNwUPN+S8eAuay/cQrsce82T9fLcY8NtQZ3fjkzhS4ngsCxLIrbitqAnMjieb+NyOp73h7S0tuEPDy/FqjfeQhjuEwORdnyEQaNGDHDfADMDHSkmNxFikoGdn8Pnexrw/nsfYtM77wuI8c57H2Dzlq3YtHkrNmzajk3v7cSmTduwcfM2bHx/B9Zu3orN2z+CoGo8poeDUq8Zq9e8I8f1cOf/bFhAOtpYkAJ0XVv3L+DgmhuciHNYkFBs0uJ4+tyzczKTqTOMOhCS2ccgi3SYjeiOnBQO5GUgoHlyRlINquGZil96xo6m1Hi0oZpBENcuccde0ubQybObJG8zaOFAg/dIFxudvG9k6Pkyo0+nV3dt71ZONFDW56Td0BnNPIiDacvGlUrf941IcRBOukiHOGIlB5mzszJDa8AcU9fRLsTmfRoEs76f98zMhyh59A3LkjqL6Y6RD+tN5CxOHkPeXSlXjZTWl/x2Wcc8K517ObSIfvC7VSvXo+DtRWg3RyH5cRpy8q7u/9Aicla+GF0QgRZRnXP9HZOpJ4aRc3MxJnHYKR85UtPQpLJSnum4uNFmoV1ny3Uwot9KnRv9ima7+T0bpg7SmbcOOKi3orsyIG1S8EpmhXSWnN9Qz1MBkx/NqLtwQo2cYLkMc8+ETXLqBZ07llUCUVimzk6qzqo8qG/yHnXS49GHmkp1rHXJb+N1KHXj6Do8o3PUS0ZtMLGuWLbUnbQbBUHMu3HjxLw1/9LeEdLWREdUl8UmSASBRhFQtipf0qfAiuW0FqMKjOzZvrVN6XvSdhyzNwI3R9JdtFevWg+fS70ITAUFOfbX43G1Ep6ueyoIeCPtmjLjs9JGnuTHlMmr8BcDXA0/Rt9Is5GF/C5+w/bgSl1rHRi9VdtRLNf35R3VNyPraKfwSOfIN6MHmKSeRZ5RmycYUKwj0yZpswxd5r3v66qWWbKh5PdkksmH15PRf4kMagyR5Lp52fy0Cb4cL+hj5epVsMNS1AllLLrAje7Yh7Du/JJdiOvjyfzW+uw6UGJdEeCQOovavMnbtH/z/0Bd31i9tgjExqMNzG8660dMfk72LJA25DbCk6ROC0FNJs/NwaeTGCU6NKWkecteL9zvhRuUSeK3OWTCQK50WrjZozhObKPyTg5WEEj7NeW7bjNctxW21yxLrOQ70i9tnHQRoGiUZN4x/xt6+Y7QylOxvEAmHzgBQZp5UhZ54Ts8Ii8VshzlV3mKypB7+ptlq/z4rkmNRRqZF98RXkOWp0dik0cmLhWT/W/CPNIcqBdlxBNZmHiPiXVBOTfCd5q1f3RUDiIvr1n6UMNvvE6Fdt+T404NH1ouaaOMg4gHlZ3kUeRR5RGXLZ8b+Wp0qQLWLJP/EzjViSwu9VT+TJ48uUQS61yeqRyNHoVOXiZ7tAwjH5WByNrUtehCY0k/utR96Tt+o7Rr3Rh5smxTN7xSppSt7ZO+AJbHSLd2oZEyM2V3rROjz7wehsao7pUG1TetF/1OaBA+qNeG5rgOqYyYN78jndoGI9q9PFZW10Z6wuVTrbAs7UcC6pHtF9sD98cgH6Rf9UXbkfAaBDK2YPvjO3JiXFTHpr2W9KZZ2qq2RZWZyNEzPKkeCs1Ru9LnlE9JXuRXdVnbo3mHfKosTX7aflKWK/vc2HYzCvaneOOJMYBP4GAh0EQggREGZehs1oSmCvkfTXx+8qmzeT7AJGXMA5rmo7N5IQ61aNLyFqL4ntDBb+bpvcYyoLGiSMOhljIcaq5AZ9NioLEyotGUsRCdTZWSpMzmeVHZpL+Up5RFnor8Gv40H9KnPJcVyz1ZGRTzaoxo4d4bTbcAbhVeXzoGvvOJREnwRClGCThBqHtgROMl9pt92fcJgNFtHKZ9b9+WeyI8rV7zlkT5advPy+Qev++vyD8dh+qyTMpGJ2J1Esb4/ua+eabfHBmYPBH+j/YuZUC58Fpdu0Fk011OR/p+SNjciIcefQxvrXsP2WweDU4I7mZMw0fnzwxMjAGXQQcHHoF2rDwqTY7LzAaygRAdAxpIGiMaKJ6Na3PzS25SR5AkbBTnixuqcRdyKp8TNotT8sbqDTK7SOeLjpzQIY4RO21bAAAOUOPghnEACG4w5N8T512dFzOAFOcpyCLr25GDpk5AccAfHQEmA/QoPFUdXFaeAVOMQ2ScLXVu1PmhM6JLDxTY4L4D6igYp415G3CDg3nyx8E5r3yHzjcVRhzuLmCSmXnh4Nw4wOqQslKVZtKkTm7RUYocRlPxUoa8r+ALvzMOv1yj4ySFX/JcBCpKDjjzUhCChkEduPigns+EL4JNES/kh78pHzrOpcYRATCRkyZ1JTOZhl91jOm0EGXVs5ULqF2zEa7ViEzal86PMhGAxVVgSHWDgIiG1St4YpwY0mzqPjr+T06XaFKgwuexrhFIJM5mCYgydUS+i7KL6s3IWOpDnFatH1MXUkeSX+T0FgEOdRz5nXHu1NirnCgrKS/KkzQouGF0hpsl2dJZcCBEntl+rVwjaDDZ3nhPj8lSedPZkj0/ovpVcEoNPeuAs/hMrC/qgAGv4nWvdUXwiW0ipgeRU23AN5FLBETKb+HbvK96ofx21wWjX5Gs+Z3IOgI2RI8jR17aaxjZhBg9kcOt4AbLUidTHNsIaKK+8pgwdro1NW8jm1Vjbe4xyoFRJ9RfYwdMe1OAyESDGSMfgaVFekvllr43dBsQoQSEiYwF7HOL7azUbkugpAFV1HYYWUUAhehKWLQLQrsAe5HuR8+71gefqaxNeyp9p/kbW2q+U5Ao4qUH4AbzZZ4no/+UTYOjgLUAT7KJbwF+kEPNurVIu7bYVulj6JRK36Cb3vY2uGHk8kO7csBAmhlpwGs82iD++4h8RRtvsl2wrbEejb2nDeFv9gHxfk10K7KBzNfoluqCgsnSNwYl4Jv1S/CyaNeL9iAOdkYTEQJeql6p3SjZGrHdBmiO9Ja6r32TzmiLLjpmsEdbG7PnURiuodnkr3yoHTV9Ivks8aptrGjPTZsxIGm8H4yAZtptpVcnQxid1b1c0sZkxhFaB6VNhUkX60G+i/o+Y3OFL9Ih9qrb+EFOvaLd1eU5aue79kfKZ1fZluyrvksgIx6Jx0EqN+Ssrt0Y9R0l2yO8dilP65AyNP2W6pHaTKVJ39H+ObLxXfoH1UHV31IdFOtLbCPrTe0n82EiLUqP1j/1j2O7Yj8k/R6/ifomc+02bjL1o7pt+jHKTHXFfK/9DOk39lbrrGhni+8rncqP1j3LELoMgFus0xCr160T3aBzSR49LmfmJATHkj4jS5UW/s+yyTv1jhui66SS1r+0O+qPAWyj8YzRR6EhotHIzlxL9VSSv6FZy9f+U/MyfEf2JJogo15LfcTGoCYP+h9B2Cj0ZzI5tAa78eojI4FwsTrvAj7QoS8DwYODBBBaDMhhHP2TuxJI6GyhYz9HAA7+T2DjYOvCLuUcaonea5wPNBIA0feKdBDkaFJAhN8yDwEOovcJZghQIuBGhXzf2TKnBJoIuKH56ncETSJ+Ww1vsedNLK9n4AbLIZ3fEtjYXwk0RxEguXIg/B1efXQMwuAzAYIbbE/8Qp6SF4QErHh6ieqc0eVT8UrbyAkGTiaYjahPRTkciWcBM9nmnVCi0dl/cKxCeZlnR/p2iLu/CfctfRgrV6/R3b0bW5Ft3iuheTwhgmF6h0uMtmBK2HyuqDFnzTgDkuTZwrIpnW6axnzEeEsIPzfp0nWpaYuzbqFEaWQyATh7mgubwfWrWdeDwxBeEwlBIxc5sMZoylUG62b2ngBCqwyCZAaaG+zRkBdnW3Umm4Y6blR1wEEjHzkrJooh6vhodMXgR7PsFKaJCCBgIr/lmUZrlAbquhmfcUJIr24AqN+nAzcCOEp06eDNRHZoNIgOTkodY7ED4vGiUSdEQy8dc2y2vEulS6fLcthptUaDJO1ItfMxnW3XzlOfmXslZ6Y4GJAIC+4RQqfYRNKo0Yo7SuRBNj2M3lH5ceZbZ5Bl8CoDDPJpBimhzJLI7rw5Hynfw+s1tUhybXShSfIznapxwr83aCjOnGo5Sqc67yzb4hFHEoGgx8IJGBI5g6wLqfdoF26RcTTb3UVmxQGSkWGproqDw2jQZvTO0Em5MOn9aCDBgW601wF1suQcMH8dwJsjPzlQZDvkTIlEHnAw6RWwevXbMnhkPtQz5i8DGkY2OdEgJtABvLYrHeSYQQx1hzJlCHZo0fk0jjuBODodtuRr2oXyEUV0SfvRwbLRQcOvys0MWulwmignrXdtSzqglPoxjkjklDMfafds53wWzcCzbkhDSa+iyAPWjcheIyK0nZT4p05x1nTFmnVwcwTUAk2cYWb0msiAstCBmX4fgT7Uw+JgvHvdm2cKrHGgGI8o4mDU1InkHYFA0oYJKokjznanzh55NgM8/ha5xvSuqKcS3UJwRAfpRv5G7iyTZRt56WDdbBpqIsdUf5mH8leqD37HPM2gu0s7KA7AY7I4yj1Dw8nqPwFkzkByoCS/nb3Ipumoh1hV+5YM6mUWMpoBJ9huZvZlhpUz/0eLTDgFnq14k5EbXHLXJHbE9OuprOnDSw6J0aHSNepz6PxHEwSio3Sooygwvmt0Vx2ouCOjuk0dpK0pOq7UmWJkDdsPQ2fZ95h+W/sH1U3jlDPfqC8p9u9RZJWvdk4ASXGOSvZH25KCuuwblFa1fWwroqNR3672Jmo/sX6W78iysCCK3izaKpZrnEaVFcdBjPojv/osssEC0hsHTuXCfLUPVZunfa7WB2mTthw5e2L7ovZKPmnThd/v2YFS22b+4rCzn4smWdTuaNQj8zR2SsumPdJ7RbsiZWqd6r2SvjB/zrLzKEbaEk6E8TfHkytW18ppeWqndPzDMYC0Y4tjNoJZBKuj8kQfdDJI6DJ2hfxFNo/9kpEJ9Y/9h8rY6BzrILJNMdsmNlDkqHkxP+qB6EaxXH5LG6y6SrqNzDTPWFki82jMaPYsitpBnJ6iDKPxpOh5UV/Ufhu9135N+RMeo3pV+em7hg+WYeT2+urV4lRy0pHjdB7vzTbOZTg8RYL9uMpNdYy8UHbJQCc5tF1Sl1SGJu9SuSoXU562SaN7pfpiviYZnVL91PZdlEVRn0wb1bJVDqoPUnZxjO5LNEDKsuXKKJi8/xFeWToaKNwKtFShY28FOtrKJB1sK8N37WU42L4QHW0LgdYyoKUHicDB3gVA60J07tU8WVbn3gp0tlYBLYuFBi1jAdCyAGDkRPNidLYuFto695YBzUzMax462hbgYFuFPNN3+R1prIilMqWd9JMGPm82z6v0NyNA9irfRT7l/Yri857xXgbK81B7Ob5pmgO0LVKaWy6gdwAAIABJREFUmhcD+SV47Y8XI5f7WCIrpb3Yjhwlms44sLKcOG+JIpI08uhU7IvprNeuf0cmFejAG8edV/5/KsokzjNlwET7sG7DZvltTiGLv3e430OC9hY8+NgDWFvzAlrzn8G2P4DjbENj8Cn87HYUvI+7pEb3I2j6FI3up2gOP5PjHpsdvU/Dwt2KG92P0ex/KoamEOxAi78Nzc57aHK3osXbgb3up2hxP4Fvb0VL4RM02Tuxac3rcC2GoLbL3hJ1NqM8vkTS/Ropd5848nTmUx7Xuh6QlHYOIC3P9oG/U8638v6eYB/qZe3fAVj2AWQdfr9PnjV4XyLltYLHf/GceqbS/y1oCHifSctKevvQ4GsiHSyfz/heQ9Akv5Oe0sMTI0zie3ynPmyR9e3Mh3TwOcvW71vlGWkyqd4/AElBqVx+Szq5Tl5o8b5Evf816r1v5Wroo6xK8qKc9mnyWpVXl+V8HfHDY7kOSDLvmf9Znt5Tvsx9yl3kLPWidcP86v0vZaNTlTt3HjflUrZKc73UidYL5Scpql+lmWVpPdMR5J4UXJeeClqxy84jlW/HK2s3o6GwH3W5duzyW2WTG5aVdtskiW5QP6Jk6p10N/gHIhp53ScybnAPIul+q++bOqFORHLhN5St6InowQGpJz4X+VCPJEVlUseiuiryaHgVfTL6q+9pfUb6Z3QyaCrqoGxYxuUWolfU8S+Rdr6GZX2NrP01ks4BZMNvkci2I5Vtl6NWE3Yb3ljzETL+12gIVE8pH8tW/SPdqi+qxwKQRfmbdqX1oN84FtvQl8hKW2O7aUIyyCEZFEr66LehPmB9xNtFS1E2Wj9Gp8z1ALLMV/LWOqQspW1JezO6Gck6audK45daR2ynlJdpG9ImS+1a23ervMM2XWw/Qmcrkrk27HIa8dr69+UZ9cYKv0Kd24Z6e6+0V8pNbIe3D3tC8qm6Ju3Y1L20M6VT7YnKVnlpK9oxaeNGn3zmo3ZL7dyXQgO/p6yZjB5qfVBuLMPoXpvubeJR7koXy1O7pvZLdJH6GCXWNRPLoCyMfFRPWiP7xHKpIyW9lPeMXkvbLtHBZ6TvZK6m3rQNRbQfp/5TJzPZNqSyLXCDb9CQaYOd+w7Z4Gu8vHqD7MrPHb4Z/WU6yeLgXkD7CMgioCVRTqfY1QllBj3FPtdrBvcNonwYaekwMYy9CObq0qcu/0f7XwgIKZEV0ZIf2WNInTuCpfyGTrQ6KOr8EuwjmGCccgMiGhDVOEt0gNSxigD2ogMfzfrFQGN+Y8BZ40SqQ0UgQB0u/b/kgCtQo/sf6eaQEYAfOYgK0jQVJxHEgYxOhxK7SfmIM6gOIXlSng0wQEdTHW2WbcANpa8EAhowMy4j8kOwSJIsp6JzZ+QZyTE28WJkaRxMvarja5xRkavwxu8JlOtkh0TrCbijEQrkgbwX3y+Cr8ZJVZ5E5gIYmP8Nr7zqvj0EjVO2L4mRu2knwOq1G3X5nyxxpkOtkTmB1YTAIuCtk1QqO4JHYdTnaASo1puWQd5MvSg9JbCK7xGkYB0p4KH0C1/8LgKH+Jz0ymQAlyNGchanTCJs1YmP6xXlrXlGspRvtE5VftSNCHiQNhDXLbMsMFpiHU2gdOVLJ/dIi+Qjy+gImsfpNvVx+OvqtW8JoESQiXLXZZdNsgeQ1IVMsHGDc8ODysrog0yIRICOkS15Nrqmcov0JAa4GACG78Ujjoyc+VzfMUs7mUeUj2nHRfvCZadxfYh02vcl8pKykYnQIEDa8ZFzP8ErS38B5O9HR+M9+K75Thxq+n3X1HwrOppuBRqX9CwV9PsO5t+8BN+1LJErCr8H8ncC+XuAwt2Q/wm2FH6noIvcvwf8TuhgPnze9Dt0NP9O8uAzmPtCJ7836fdAI1NEP8uTdCdQYLn6v+ZvnplvYv/zG5PHSVw7m+/Awcbbgfa7cajxNtknRPgNH8QLD18G1/4QGc8R4EmW+dquRAzJMis76pdP1f7XDWQp1Ssr3hQ7xAhigh3JrCP/y35Pp+K4JKYPlIef51LGAJQTo0ll3zI3h0TGPuq4bcjexnY89dAdePkPN+L1h8dg5ePnYuXjZ+PNR89DzaOj8ebDTGOx+g9jsZq/HxmJNx4diTce0WerHx6JVQ+dizcfOh9vPHwhVj52IVYuvQBvPnY+Viw9B688NgKvPXYuVi0dieqlo/DGIxfJezUPj8LqP5yH1UvPw+sPjUD1Y+Ow7KGbULtyI1ZWJ7B8TR2eX1uHvzHVNuDZ2gY8V7sHz639FM+u/RzPrkni2TVZPLcmiefWNOC5NXV6rUnLs7+t3SPvLa/5HC9Xf45la3bh+TV75H35lnnVfo7n1+wqPtPffPfTKPF5HZ6vaZC0rKYOy2r2SJK8JI9deHbtLjxby/Lr5H19r0HKe3bdJ/jb+p342zp9h/kxD5ZVSvw/ol94IT+aTNldr0k8X0O+NVE2xfJrknixugHLq+uwvHqP/F5W01Ckm7SxrGdrKZ8S3aY8kXHtLpW10FSnv4XXPZEsWD75Iy8mP62rZ9ZFdbaWZTBp3envkoyUPv7PetQ61PxIax1erNb00poGLK9J4JX1GTy/Wuvi32tYj3V44a2E6AfzLsq8piS3ZdVJLF+dxovVmr/SsAfUDU11eK4mLbJkfT5PfTA6IXWt9U66zH2th6TUbfH96BvJI6YvRqaG9/g1rtPUgxcjvTK6wXpgfrxvZEE6VM9L/C5bl8HfVtfjpbUpvLY+jedWfYHl65N4rjqF56uz2m7WUJYNWL6aslX5PLuG7SQteib8RXVp9NvUq/Kg+mbqnHSxPS1bw7aiiTw8Z/Qm0hXDg7wv/JXq1fCkuql1bsqM82n45ZU6W9JPU57qquFB64D6UWpDkkcX/eWzSJaU7/oknuHzdQ14YU0Cz67ag+fWp/D8Btaz0e89eGbdHvxlXR2o45QFaVd9aAB1bVl1WtLzNZRrsovuszyTl/Ji2kVXOpX+kk0y8tcr8zC2g3XwOV5c8wmW1X6i7bm2QXWFsqZ9Eb1U20LdY7m0CUxG1uYq+riGtkOToZ/PVSdVH7VOeS/in3IUXT3xa4mXk9X/OrxYuxvL19fj2ZpdeH59A/62ph5/q/4Mr274CC+teQcrajfhzTUbwD1oqmuY1kvi/6vW1KK6xiQ+4+9T58oNulasegur17+HN2s24Y3azVi1ZjNer96IFavelivvr1yzSZ53v/IZZftmzUa8Wf0u3qx+Hytr3tX3eX/NBvm9smZz9PxdyUfyrNksz1bU8p0NqK7eiJrVm1C9ejNWVW/Gm/ymZqOEopJO5s+8V9RuxMra9fI+v5GyWb81zIPXjVhVXaJXaWY+fLZer/J8M4Qu8iBJaSy9r/nwnRWUSa3Sq/koX7zP9yWRH0lKp+a5EW+uWa8yEvm8q/QJLaS99K3ya2jZJDyQD8oinvQ9lY/QVrtJdFzp3hTlr/yybMoqnkSmxXxZH3G6ma+hwfwmD6xjLZPfr1zDZPSCv1UHeL/0XN97o/YdvLpqLd5cuxHVb23GK2/Wyu/XVr+F16s3gPUvOlBDPjehpnqDpCLPUt4GvLp2I15ZtzGqM6MjpFXlaN4vlb9J6yPSXdFP0TnlR2Wr3ws/Rg7CG+vX8Kh8GPmKLAy/Xeo7klf0TORVrfVNmkx5op9Cs2kTpTZj5Kc8medaR1pupEsRz1JXLE/amaGzdGU+bN9r1lEvNmBV7dtgfVDur63aiNeqaR83apuK5MQ2pO2KstlcbGdsm+SB77++VstQOrXOmb/SoXJfRd6rTfugPnZtl/KtkSN1SfTL1CfzVH0zeiZ2pcbYDy2TeVBmb6zbiDdq38bK6vUCmm1Y+xpeemQKXv/DBLz62C8E6Hj9sQlY8egErHzkUkmrHhmPNx8dh5WPjseKx04u8ds3H7lU0opHL8WrSyfg1cfHYcVj41D98HhUP8zyfoHXH7s0KmMcViwdhRVLx2CloeXR8Vj5KL8ZL/SRzteXjsfKx/jOOPB/zXcMXn+c/tUoefbq0vFgKvIV8cFv5fuIN/n/sQlS3puPqAxOlt/u35H/6qWXYeW/XYzXHhyD1aT94bFgOdWP/BKv/mEqNtYuR21tLWpWr0F19Rqsql6NFatWY/XaDVhZvTbql0+tfjc+zlhdvRbr1m/AqtW1WLvuLaypfQs1a9ailvJ5Y9UpNR6Jy8WMw2rYh72xSuRRu3a9yIlXyo3yMu8d7jqkLWzH3/6wBF/vfhSoXwgkpgMN1wPJmUDdzUD9XL2/ZxFQtxBomB2l+UD9fKBhjqbEAkDSXKBhFtBwM9AwA0jPQGeCv+cDiTKgYZG+VzdX82+YBqTnAbvnY8XDV2H+3DtwzbzlmLzoJUwsX47Lq16WdEXlK7iycjmurHoOVzBVvoIrKlbgyorXcGXFy/qscrne5zO+W/k8ri7XxN9XVC3Tdytekd9XVD2PSRXLMLliWfF7/p5c8TwmVzwn10kVL2NS+SuSJpe/jMnly+V9/uazKyv57TJcUfmyJNLC+5PLXsGkiuWYeMszkqRsoWm53Ocz5sXyNfG3lsVvTZJ7UZ4m38llr2FSuSaWR15N/qTr6jKm5VGK8iLdUWLZQnMV6V5elElJjkqT8qXvGjrlnQryprK4ulzlZd41cjBXfb9UPyLv8uW4buEruHaRypXvkCZ9xnyjvMuWY9KCF3FtxWuYtGA5ril/FVdVvIqrq17H5QtewKSqlzCxajkmVkUyL3854oVX8v0arl24Alcvop5QJwwdUX1H8iYvpH9SJetd9UFlZerxZXkmz4U2lrdMdJH3JAn9pTqkzrBMw7/Kg/r5stA7UXRU+S6WVdQp5qNJZaEyYV6mrrU+lmNi+UuYVPkqJi1ahkllqs/89qqK10VHrpD28QquLmNS/kUO5StwZfkK0WuVjdJK/lmnfJc8kM7LqyLZUU6s+/JXpI7kvXLKTJOhKa6zhv/u/DB/bUPUL9XB+Hf6TOXD5+R7YtUyTFzMdsz0nLRvPjPflfRbaVfboPVQfIftku05alPXVL6KK8tfwpVVL+HyshdxVeUrklje5eUsQ+m7fPEyXL5YdY22p9g+jW0oe030zbRNyt3UcUnvtE6Vn0gPquJ2I7ItFapT1EmVX0mXRMbUuchOXV3xDCZXPqt6Ual1fG2Z5qP1oXUm9rPiZVxbtgzXLdL6Ne2MZbCOJ1a+hqsXvSa6wvdNu9K6Iu1q60hXSdYqH9av1sXxX1UnTF5GH1RHu+sLaf2+/i/DNWz/C/8dv6x8QWzgJNZf2TN4csVWHADwLYBOxP469X/eO9XTIUA26UzazUhYLUg5THs1SsHfJ8eN839z/7BXt1mOd0w57UjZ+5F02pF09+qpUQ4jL1vk/6SzX55nbD7Tcvgs4TeCp8jwftZqR8beL4nvMx+NtGkE8+e9er8FCa9Z3y/m1YKsXUqaP99vF35IN+9leDqT3SLfCr1Oe3Sf9/guk8qB9JB30sDTyZiUr2bJp8iXq+9J/vzGVj6LcnNJewsy1gFJxfsiV+Up4bZHZais+I7IifxFqSR7Q6fyZ+Rd5NF8Qz547KbXiISfl2uScmMEhsh6v8jb8EjehLaoPk25lJmkSB5Kf/Su0Q1+E8mt+zXpcGlyqxz/mXQYPaFLaXmUPaO1WJdMSr8usWR0gebDciiTFtT7zVL3pIt6orqismDdZS3ysz+qs0jnXNaZ6pqpX+VT65t5lOjVvPhc61bL1f9ZD3y+N5Ij65S0xXTe6E4X+bWrvhX1T/VQeGV+oisHRK/jsleaoufUUaPnRTmTHrYTo78qP6HbY503F/mWKGirGemsRrDxGeWe8Q8g7X0pbYT6Z/hW/WiBbWnSdtNSlHeC0bSekWmknzH+RB8dbcOkkXyZPEttL64/KnfTHkU2zC/WHsmXaX+SX1wHvHY02E2qJ04TGqwCcOhb4LsMhv1oCH7+T0Pws38egtP/aQiG/mgIhv7jEJzxD0NwFtM/6n2+czLp9B9pXsyPvyWPfx6Cof80BMP+YQiG/R9aZpe847Tw+38svUM6+a7kG93/2T8NwU9+PAQ//fEQ/OzHSi954bs/jd6Xb8jDP+t9wy/fM8+E9x/1jN8ufER0nv6/D8HZPxqC4T8agtP+6xCcwTL+YQjwzW7gOxf/ZcgQdLKj7Sh1xOx3DgL4pgPg71O5H+7ohJxgx+vBQ5041KHyMNdTWTaGd8qF8klnLJGPkQ3vm3cOdx3S1vot/vjgLfg6+RCQnA1Y04DU1UD6OiB9PTrTN6EzNR1IzIrSdCA5FUgw8f4MdKZm4WB6Nr5LzcKhxEy5h8RsIDkHSBHYuBnYM1OSAB0ETpJRPskpQGoG0LAQrzx+HW5c+Aguq3gXF1e8i1Hlm3BR5SaMqtyIi8s2YkLZBlxcvjZK63Fx+XpcXLaheH9cxVqMrViPsRUbSvfLNmBc+QZctHgtRlWtxYSy9bhkEb9dC74/rny9PB9XvhGa+P762LONGFe2SZO8o/mRHk36/9jyzWAyefAZyx21uAajq2qK9DBv0tiVn1p5znuXLNyESxZuljRhkeYxtlJpJc2XLNqASxZtxMWLNgtN5HV05VqMrqrF2MraokxYNhNlxsTffNfwyd+l/3mfcmDSMlU+zFNlRJkxlehnvutxSVkNJpTX4OJylr0WpJn08WrK5nsTylhvtRhXqe/K80WbSu+V10o++h75rZXEPC+rfFvyuqTsHYxZtAEXL96My6o2Yfyit4QH5SPigTpQqXog/EsZpfojTaSPcp6waJPInfVBGRpeRaeEh01FeRl5is6V891a/SYmUyO7kiyNTCNdFd01v/Wq9bJRdEd1aFNUL/qc9JIeo0+q36U8Llm8ERdXrceY8tWYcMtaXFy1DmPLazG+rBYTKt4q0k+6qe/Ux1FVtVKPJm/SYNoZ6+qyRWtx2UIt86KqjRi5WHVMyyatm6K6LdHB/KW+Y/VPuimTsRVMqm+jKzaCSe+Z+9omTD0aHbps4UahgzSRduo425LqOvWypM9Gx6g/8j71mO02atcqww2qb0XdXI9LKzZg/EJtX5f++m2Mr1yHSyrXYXz5Kly6eI3oIPVidCXrcoPozS8WbAJpY1skz8U6FF0gn6pP1CmxMZFdYh58xntGf0ZVUrbGXrE9rZUk9RXZCvmmvGQDyR/bBdMlZdruKFOxk1IP2mZFxuWbMbpiM0ZVbBaZM3/Wr9aN2lPyd1HVBpAWI0faSibyJnoS6c/YyhowmfZu6DzZa1F2kf2kbqkeHFv/SStt0i8q3sZlizdifNk6/GLR27hi4Qo89dpOfG3GU+z5zOAq6gU70YFOGWLFgI9T7CdFQWeAS7GywZdIOK1osCKH3m6T/43zfKRryekwjp4CHHSI6Vzzeb1HR/xACdywuaeXOvQEK+oJHHAJlv0VUjadvQOod79BvftV0Tmio8T7u/127A74vjpQ6mSWQAXJJwJSSg5T3JHU/MWxNI6j0GPojsCPiA7SLzxGeRonkFfm39XJjIMYkbMsoAx5+0b4S7j7Icn5CgnnGzlOtN49gDp/r6R6T59TPurI6ZUOJeXEd3kEKfMQAMj+SmVnHPkiuKIOq3xHQIgObCQzAwSoTA2wYpziuOPJ3+rIGkdeASyVoZQv/MWAFoJSkvRexmuX5aL1Fp1qXb5Wn6WeKT0G2BGHnI43ARmCGR7l0Y6iPFwDThlwgyCSyjVlf4WsdUDBDVvlV+ftF70zzjCdZdJFnaL8MpZ+o/woIMXncsSrS6c8kjuBJ/5vdFPAupYiMFGsT1Mf0XdGLwlMmN9GH7VuI/5FD7icWsEoXqVtsD04Coipjmk+pE/aifWN8CAARwSqCX8eZaZ5Uz6pdDu4rNT194MgZr1DXdiPBOVkfdlFL/kd5U2ZONm9cATw3BvpTtRuyF8EyhiZSDksy7QZkZfK0PCqdBobEemPyJRt/ivhSduusROxOhAbonZE6+IAstmvYGe/Ev4oHy/8VttjsE8cIXS04//7p/8VObsBrpOG6yY1ORZcSWm5z2MwHcc76eTaDkxyuKegq/ny6OAcjxe2M/DtDGzHA4+M5rt+LCktFvit7fKq9PhWCNfihvCeLOvgM0lRPsyrRLcDx81Ist1MMR+WxfxYhk8ZOGl9j3T2kG9Tti4nDOFwzxM7jdBLwrd3A4f2Ax1fYcj//D9pL0vn/dtD6KRnig4c7DhUBDZOsW73e+ymUqnivYMHCfsAHR2U09//4hIwcuoUtCz+5PC/hwSNLXj6iV/jQOKuCGS4XoGNzK/QYf0KB63rcDB7I0CAQ0CJqUDyxlJKMfLiZnyXmY3vMrOADMGRaUDDTI3cSDB6YxaQmgMkZ0kkh74zFZ0ENtJT0UGgpH4Blj92Ha4pewKjyj/AheUf4KJbduK8xdtx/uLtGF2xHePKt2FMxTaMrtyKMZVbMK5iC8aVb5U0puI9jK58DxdWvYdRVe/Ju+PL+N0OXFi5A+fdsg3n3/Ie+N74cj7fijEVWzGqkmmb5M8y+Fvv6TO9x/vdn+k3Qk/Fdowu34lRFTv1W9JQuR0XVm3DyMVbcOFi0rkN48uUdubPfEcLL0o38xlTvgPjF2kaV7ZDeL2waqvwNLpqM8ZVbMb48i0YX6bfXyhl6HOWMapqi8iG8mHZTFJGhf7m/8qH4UflIzxGcqO8+D/lO7pyS1E+pJ8yM7IReklz9B7fpfyVT60r/Ua/G1f+HsZUbsaoxe8InaNYTvknwrPkVblZnjMPlkF+mC4q34JxVdswZhHrbhtG3/IRzq/4ABeVUQdKfAhdwr/KYeRi6gLrmHI1fO7AuLLtoF5QzvxN+fA9fZ9lq8z4jPUh9RiVo/W1VfSLeia6Vmny1ryUDq1T8sK6MIn6Rv1jou6qzm4F63Fk5U6MrPwEI6t2aL1Rx+Vdpd/QofoQ5VmxTdqK5F+1GWMWb8FIOom//gBjqt7FmKr3I32O9K5qC0beshkXLn5H2w/rRNrANpxftUPK5v8Tyt7DhEXa1thuzv01edb6FZ0jz0If9bDUDihr6q3RXX0WyVBkvBUjq7ZHyegkdbWUKH/mw7ZCGpiod6IXkcz5vrbT7drmKthWtqo9MHKlbIr6oXkKfaLH/F/ly7z/f/beOz6qOl8fPzRRwYrdXdfdVbe467rld+/eu9JbgBCqgl1QVCTJ9ARQsK6uWyzriiCCYqEECGkQanpP6OnTJzNpBEgvM5M8P573ZwbYcu9X3fvXurxeh0kyM2fOeZ/P5zPned7P+3lP0edhKvdpyMQkSx4mmLIw3ZKLyfoMNQdkPufLOJoRWwJuPD61D3UtwufAtYdbeDypMaDGlYyt0Hjgazh+xlnUXGWsZO4YwuuTiqt6Ta7EmeOYrwl/Lh+5lvGR44bXUI017rtQ4sy1jxvHF6+drB8GzuvQ+sD5Zs6WtTG8PnJOc90aE5d9/nPVHCpUc9ecJdfjb8d3eJx/2Ue1lhR+7fHP6zlFX4AIYxHG6/IkDjNMJZgduwdrth0XckNR+wEI5a/uq1RqBAEMwB9iPf7xl+O/+l9Jboj/SkgVQWKD2Vz6p1Q5WiW7ewGoKvB/8e8EGgRDYUCkACSBlQKGJAAEkNe1CWgk+KFqgJlcvka9V4GxMGgjwCH4LK/zo9LjFyDF97gciswgCUCCQ14vAFB9nhyXSwFXvp/7FyIidG4CnOR5RSjw9Yqc4LEqAMvzCYMwAkjuh4CPAFwBue4LCosQsaGIAu4jpLpwKUAaBrICnl3dIbKmVwFLxk3Im4vJjTYB8wKuGYNQNl3i5VJxJNivrOO+LpAbYYB5gYS5mCTitQmBwhBYvpgECF9LIaC8SkERJm3Cz50H5iFyiXGRTfYXJjIufiRwDf/ehlpXq8RXxsT5cdUDq1ttArRDyhWSGvw8NW54rh1yvoyJyv5TeaNUFAS0AqaFNOoNKTcUeObry70kjNQ45HvD15hxJ6lEcoNqmgvHymMmqcb4kmxQ40LGqEfFlM+Hj4/v4+eEx786D+4jNB6FbFLnEo5peJ/h18h7QuSGnHtImcHnwySWKH5EAaH2q8ZHL6xOP+xCcCgy4MJ4Zcx4bN2wOnvhdvQJCUCViqizvPRJ60IV/bnq+mQ/JN7C58LxxZ9dzja4nIrY45zj3xhvIVoYNxkHvefnhRAUoTEWjsXfPqpYh0iSvyU25BgUUSfkyUVrCMenGvucN+qzw+QGfZec7m5UW8+IFxxjLfAw2Ic7v32rKL/4N6UQUiSfHFeIMFHXIEQYhtYeFWMVB8bxf/s9fP1lPHi4lqm5yvdwvHA94XXncVfSp01IIDXWZE3iOLpoHeXP8neXHzUuvxqPIcJT7UOtJbxmjLkcnxCmYZIyTEaFPyM0JkPjUdYJzrfz5/q/n9//fv7dqHb1yHyqdnXB6u1CtfjDNKA/JMnQBg2T6xHkReEXDvrR38/v3n4EB/4N4BmRmpoaudUIg/ZgkMEDwo/yyzf0vzDJw9jYbDaEY8S/h3/+n0Kj1bf68P570eipfQGofUKpMWqfAqyLELQ/Ab/9UXkUBQbJjWqSG4vkeVQ/rn6ufQpB+1IEnUsRrH0EsD4I1DwqJEfQtggB+5MI2pYgSIWH/PykUoNYQ49UjFTEIOHthXhE/64CuWaCsGyMtuRgjCUfU+OKMEGXh0nmIkwyF2CiIUPAB2/uZ5iKBPzKzbYlG5MtmZhhyMHUmBxMNZVhkumw3OiPNSvgMsWSiymmItkmGvPAbYq5BBFxBJgFGEtQac7DJEOOAOgJxgIFlOMUqSKZUHOuHAcB9thlOYgwl2KymaTMAUyIywQ/a7ylKATQMxFlLsQ0Hn9sHiLiSjHemI0JAqRyMMVSiMmxBZhuOowpAuYK1efzeUuBAC4CLWahZ8VlY6Jur4CMcaYcATOMDcEKj53gjPsmYOH+J8bx73kYSzBnKZZzFVBgLsNEQzGmmMsUgAkhrls7AAAgAElEQVSDYUOxIpIsuRJjRSIUI8JSpECVWRELkwwF8j4FzFXMxhty5VwknqZQ/AhACDL1uUJUTCIJE5eP+3QEXScw0XxMwA1B3FgeN4G+sRijDXmYEFcs4D0M4qaYGNNi3GcqEBAfEV+MyaZSuXbjjZkYR8WOORcTdFkYH1cgwFGAloHjpRgT9eq1PH+SJby+BJmM8XgCaBlbRUKcEPQKaOJ7LSVybScZ1Pgbp1dxZZz5uqm6AgHIQkaYczAhBJJlnApZdjEBoEB4BFU+zKgbDmLq8nyM0edjrKlYYsHxMEVP9VKeAtEGgnjGq0jOKQycBeDrS2WMMzYEpYwVrw33MU6vzo9jgnEYz33G5yOCr4s+IHOE7yOZSFKLAJZgkZ9L5RTHOUHuhPhcTNaFztVSgolxxRitz8TkuHy5tgTcvL5TTAWYbOL4KcQEjk2OX0MxJnOMcSzG8xqrePNnqkUmWUKvsxTIOOV45TXhcU7WZ2IayccYRQ5OMXLfJaFxWyL7Hmc4ggnmw4iwFGBC7D5EWvIQYeI14PwkwagIOcZFrqmejyTaskMETz6mmQoxleBYl4up8aUyVybpQ+PWVIgpcUUYF5uLCAtJjSKZozLW4wswnvOS64klHxON6trz53GMgbk4tG5lYbIuHwTe/BwSIxNjSSKWnJ+vjJHMR1MeplvyMGVZHqbpSzEpvgijRXmRhwhjgRwrxyHnFMfxdFOujBXOGRIYPH4eW5jcJNE1Xp+FSWbOlSLMMOdisuGgECuMDef1+NhMTF6RjzHGDEwx58g21pQpr+GYiDAcRoT+GKbqjmCqifEvUESjEFskkb7ulo8Jxox/YvznCwk+2VIia+0ESxEm6goQadiL9xLK0RYqQQFvopgJ+RtyQ4ljv7k3WLzXFLAmYDQM9L78I2+Qy+t6BYDyJp7A86/An6cDlTSvre8UQMUbe6eDALUFroYeVEomvRPV7pBRLkkGV7vceJe7ei+QG/azcNtaYa89BVcDb+JPo5yZf18fKtghp1GBUTFV5vE42mDztqHa0yKG05WedtkvzZhpXE0Aa/N1oprHRvDt6pBj4GfzNZXWs7D7+PntcsMuQMDeDYfXjwo3jcBZZqHIFrerVcoGaNBcTkDm6USV7SxcNN91sL0fjVO7UO7qRiVNbz1nlCKGANPZLp9L814BWaHPp2E3P4fn6XGflRIBAl45D4KtcPmP6wzsThoEK3Pgk+4zqPEqwFNlV+CmxsdroBQT9roOOOyh8h8aZbtbFbivaxfVSI2vDTbnGQFkBCs0Cq91MUYt4Hvlc3ldHCTAOlHtUiSVAuv8PJX1V5l9RR5VO85AqTfaJdaMRbWTJU99qHZ0SnwrnTw+lkhQTXBWXRNPlxAgNV4/eCw8LpqM87NomE0VCD+fseL+aMzs8Lajys5j6kBtQ69cDwdNk1l2JcCzQ2Juq6NaoCP0nk61P4JPR5sakzzXkGqB4NXa2IcTzrMSL5pI81g4Zmn6fpKxq+uAzacItWpHi1xf+TySUiRWfGdRZT8lseS1kmN3t8tnVYfGHseFnUbVdaEyHIJ4D02822UMCeHoIvnYIbGvtLWHiAUFmBVBwbmoQDQJHBIgTlsf6miyb1djgMdd4TgLp6dDDMZtjhBJxLlIdUsDFVOdqHWq61TReBYnpZNSOzwEsDQuZ0mMt0eNB2cHnN5eiSGvi1wbb5fEvrJePVb7ulDh6VBG7O5OuOv7YHOqecPrafd2g+OV14XXk2OAcSIpYfOxdIlKng6Jl5XknoPXgKbb7UK28D2KRGPZUEtIKdCP737rdlmTSBYoVQoJIkU68PoIgXh+zCqSKEw+fJlHjjOa5FewwYBTrWE0qj/hbUVlfZj0VetB2Ljb7mwRc3jOJY5bxlL2I/NJkasutxr71Q6lMOI1YoxIHnCNcnq64KFaydaJGs4hTxfsMl/OynrgpsG+U8WoxnZWVC1ck+Q1HPfuTtlH+Fqq+frVz1+IVacftc4galxBMeZnTKm+kuT6AKANGioKDSE2+FUbIjj4ID/+T8j0G/T3sCLhG3TKX+tUSW58lX+at60B770Xgy7rC6rURBQXz4hKg+Uo/Y5FCNhYOvKklJj01y5Gv/WJEKlBBcejQPUT8Ft16KxeBjieBDxPoL/qIcD6BIL2xxBwPAGSHEEbSQ4+hggSKU1hicqzwMkY7HxrAR7Vvyugb7IpA5PMBzEpTsmlI4wZCnAZ8gSkTTVlINKUgVlUcEQfRISRAC4XAp5NLEPIwgySIPp8TNArID7ZUojxcTkKROsKVBbfUiTKABInY2NyhQAgEBSwaMxVxAfJA4JgqgsIZijxji8Q8DiFAMZM4JyrgMFyKg4yMNqcJwCdAFiAWiyPP08AlhAqcczY8vMKwX1EGNQ2LkZlRUnsjBGAoUATQcx0ZuX1B0XWP2l5LghABPDHZmMiASYz6jxnEhsGBT5HG3Mw1lQggJTgVsCLEA8FmGopVbEhgDTyc9V+BKBSiUE1AIkJ7ltIoByQUFAZ+UIQVEwwl8pG4oTnws8XYMv3c5+GPAFkM8x5ISl9ImaYEjHTsh9TdemYGpOGKAtLKHbK36PMuzHTuAczzGmItKQiUpeMeeZ0zDWkYFpsipwbiYtpywswLvaggCzGgOUE0y37BbATpDLuk+NyRH4foTsYArvFQmIQ+PL9PD8hgkJKGo4TOQ8zwVuuZPOVOoTZcgVgx+kJlovOv47AmEQElRiM7UReM8n4k8wJZ+wvqDsIsoUEEaVKBiLMh4TMm0AiY3kJplAhEZ2CmbpdmKtPxFxdMmbpUxFp2I0ZxlTMMCVJnCKNSYg0JiNKn44oXRqiYrdjtn47FsbvR0T0Hjkm7k+N2xxFbOlzERG7D9N0ezGLxIRBqT1IFEYZcjEzhqVOOaHzUc9NiMvBGEMWIuPKMCk6V8Y5QfzU5YUCmoUMMZH8KsDY2CxELD+M0fpcITI4hkkaEgxP0BM4K7XKOJ2KEa8PxyqPkUQMSQSOH16TcSxniafyJVuIGiEpdaWYEFOMCPNhIXEm6rPlcyfF7sUMwy7cvzwRM2M2Y45hByJ1uxAVlxaKVxJmGZIwR39hizImItKUiFlGjqs0TNdnYzrVD7EkOMpAcoPE3hhDDsaZsxBhzsSkZXsQZT4k5VBCZJAUtVC9kiUEgag/jFngtRyvV4QU98G1YZalBNNicjFNl4NIc6kQBVR7cc1SsaQaplTWGI7r6cYSTDMUY6xOkZRcI7iW8TOoZmJMue5MijkkZAjfO57qH32eEHFjdXkST5IH0+Jz1PzVUzHEOZ2h1jILSSmSO8VyHSbHqTWM50biioSUEKG6YkyOKUOE/iimGNWawTWCx6CIjbCS5qs98twZVyq6vu74n2FIwQxDEqbqEzHNmIS5y/dhVuwWvLelDF3Mfsi3YQAY4BYqaA19QzJ79E3+d4HcUDf84Rv/L/vIrF5lqHyEGd3z5IZkr7nPNumsVOFoQIWrEzZvQDqhsf6/xt4kQIhEg72RN8dUi5wRkEjSw9YQQBW7NHm6JIvsdXfDRYDmbES1uxk1vi6ccLIbGYmDM6i0n1Y373XdAjwJFlnyUu45K68Jg+pKRwcIKPkeWz1JD4I+BSSZjbZ7mBFVygkB/+wu5qBygJnUDtTWt6PcxfKJrlAmW6kDSDwQwDkaekMA7TRc9e1C9vC8SDoQNAoh4GoJgdR2KQMiYK20EyB1wFPXK0CJpITVpwgju42dw1g2RNBJcKKIAAI6Av4qxpIkBlU04cx2XZ8QCLW+Hpx0npXOTwTs9GBwuTtwwtoMez27bSlwxeMnySKeFgIAA6ipC0q5UrWjGSwrYSkJCR4BZq5TCni6FZhXJIgii/gzCQCSCnUNHXJ8PMYwyVEh58OSI3Z2C2V87arEh+9zeUjonIXV1irgjUQIP5MkCAktElsEvNwYT3djL07amwQMk+Dg9eR1FvKMfhPesyqrzE51Pp4zM9eKZFIkBkGvigNjIgCtTgF1+Ux2zyJZFupuRWLAXt8lZBPHH+NOwoD7dTawI99ZIVEIxKXrFDv8eUjokFxh2Y0iz6RDFsd6XZeM+wrH6ZDPzWlFenm6BOgzbuzcZfV2oNLRJOOq0k6ig4SKIpTCyg0eixoHVNj0wmZT5Rucn+H5Rb8NH303rI1w+JRqgyQQVVyVthaZd/YGoMIbQEVTJ465m4TUcNrahBTheZysbZFYEiiTUCKZWOk4JbG3eXtkLpzwKOKntr5byCF7U5+QC+U1LXD6qC4hcXEW5fYWAe9yDVxnQv4ZbXK8fJ7zkAQXu9qRBORnne+u5WbZE4kzxpjzsvE8ufGdb39PiDquUxcUFiEySK63UlWIoiakjhGgz3XrS/wu48hHYrRVurmQuBDysqETx0hseRVJ4WB3QulQdga1tiaQfJD98/qR6COx5zoDl7cVXpYU1TSFPr8HzrogqqyqMxnjJUSdvQluZxdcvL7unhAhy85WHYrsdJw+37GRc50kBhVAfC3XD1nfHG1w+nh8oRh8ifP9uzjxPVTgOFly5z9/fahiC3tpaNpg9RX7V4kFRWz8m9xQofk3ufHl7sK+MrnhbO3B2++tRIf1VeWDQXKDvhm1S5S6wvEkgrWPY4CqDvsSBB1Pwe9YhH6Wnzio9FgAVC8+59/zIrqtLyFY/Rz6yx8DnM+iv+YxDNgeQ9DxCAbsLHfhxhIXvu8JpQKhoSj9OU4uVeSG7gORXjO7OpVeC6ZkRFmSMDsmGXNi92OWOV9ltHX7ERm7G7NjUhGl24OplixMWp4nIOl8xtzIG31mq/MEfPKmndLrsXEFiIg7gim6YkwkoaEj2C0R0iRq+RH524ToHMlq8j0CZPQECYr0kGw3AV5cASbochQQtuRIFpKExcTlRUIoTF5eiukEyrEZmBqXh3EGPrJkoEAAoGRXQwoIqg0I1ggqJq8swn2WPIyLJ2GRj0mxOYikbD2a2eV8UX6QtJDPMqjsNpUfBICjl2XJuYQz+PyMSfEEzQRH2RInqgWYuZbPC4FJgnICflGpGPIV+CHYYemLLg8T4llikysAlmBtanwxxlBdYSDYKcJ0M9Uz2RJDlkZExOeLioLHHRmTgbm63Viz0401CfnYlJKDD7dn4uNdRdiYWIQPE3LxcWI2NiVm4pPt2fhoaxY+Sc7HhzuysGF7Pj5KKMT6hFKsTbJhumm3AN4JMQeldGCC/oAQJXN02zEnZgemRR/CTEuZXO9I4z7Mj92GB8xJmBJ/EKONLDPIF0DKLPV4jhkLSxIKhVyS8cCSH5Y3GTPEw0DiFHtIyB8CcaoBhNSJJdAslvE2bWXx+XiR2OC583pKOc1flcVcKG0i8J9ozsI0kjDLDoqaYIYlGxHRCVif3oB1Ow7js13F+GRHgWwbdhaA28adObKF/76Jr9lVgM8Ss/DJ9kys35yDj9PcmB67V8A55wKVO6I+MWXj/vg0zNBtE+JQVBmWdETFp2NB9C4sjE7FTHpUWHIxTndIlD/j4otF9cQSoqn6MjX3TDlqzpiKMSU2X649iTMCXapPZBNyKVSCo88SkolkJBVMkeZiGVcE/lLOQSWFEEpUnXDOhlQe5izcZ8rFaJZYsaxCXyIKqYkxmSDZOTt+P6JiPseHqTasScjFhh2Z+DQxD+u3cGwVY/2OAnyYqLaNjOP2wovimYcPd+Vh/a5CvJ9ciam6NCG+psWXYXxsthAGVGGNX5mNSSsOYIZlF2YbPsd8wwY8YE6QccbyG6pkeOwkHSI4X+MKZa5QKcV4cP7J2vLcPkw3ZGCKLgOTYul/oRRSQjgKUZonKo1x5kwZF6q0qEDGhShizGWiaKJai2QLiUQVM87RPCFjSMhQbTQzvhQTuVYY8zHFnImxMXtlTItCzJyj1CZxVDMptdikmEI5Dyo8IlYUYLThkOxfiBWuw+ZCNUcsJUIAT4ljmUuOrLckpoRUlnKbcBnWl3skyUeF3dcd/5u2F+DzxEJ8uisHHyflYP3ObPxlay6+2HMC6744gJ7zXAbLT1QJCm+oeOMV3r7JN1j/LLlBEkTJmxVg4E0zwbVku4XsaEG9rw5Ol0dUGMecQSEW2AbW5fRJu1mClqq6gIAhZsLLfT04xoymAAPelJ9BTS2znYp0sDpPCbhjlpmEgbTqdhNQqkwzgSKBZLg1OoGqAE+2kydxwBbLvh4BJFSVkEDg88x0S/bboUDoeVBl64LLC1jtSv1BpYi1qVsAoAKUJCxU1pmZWIkJ/QxCYJJZepYcMJNKoiaclaYCoMbGFrN8T4eQBsyWs8yF2VbGtVJIjE4hKU5a28Ujga2PXXXdop6Q9umh1tkn7PTj6IWdqhRHB2ptHUIMVLB8oMGv1DNs2exQZR0SAx6vs0MRJg6+PqSgIehy+VFh7ZJsPmNhb2iDo54kzFl8sX0ftu7ajU3bdmDzzlRs3rkbW3eEt3T5eRt/53PbkuQxITEdm7amYPOOvdi265AQAVSulDsV2eTxdcLlaoG0HnV44bW60OBqhI+SfWsnahqAI84ATtb1o6axX5ENbD3uPoUad4u0DydZJQCeBJetCzYPAVfoHAjEPF1y/CTCeF0Ikhl/gnWOGwHpzla5RrzOHMckEEjqcN/HbI2h8d4NEjTiTxMqT+HYovKD442EiM0TlBhyv1RLhOX7VHgQDFdYWbKjwK0Qe05K/JUihsfHa1xtJzmolDfh4xBzVpqwnlceqHIVzj2OPSnfoFdJiORyuZnhV74nMtbdbeKz46ypQb23ASc9fThB0sDhRp3bgzoqZFw9OOkFDnuAY55eGT8sYWEJCJVIBK8ExhzLYaUW48O5SLLSWh+UscjzoeKg0tYsxBbJOI4fzm3GlkonWSu8VDGcldfUuBqVVw+vV50i0kio1ToCsLkCqsTD2Yxq32mUk+QUpQDJDRIbzbDW1Z8ntL/z7duFrONcCis3SCqQ6BFiImQSTLKJv3/lRxID9nZYa1tQ5/Ch0VMPemU47Kfg9AVQ7ewDFTa8LlT4cH1jCU0tlWFSakKSplfmpM/lhau2Fm6XT9pyO3ledd047vajsvEcVHJT3XUK9oYmWOtbRAVT7qSSowMkT2R8iBpEjRnOWY5xKRW0tyqPGU9AiAiqZDg+qOhi/L7yeV8UL17/sPpPkcT0jmm+QG4M0lTpJ79swttf//jlkO2/8Kv+TW58uYv7lckN91k/3vnzC+is/a0iNcQ4dIkoNQaosLAvRn8NlRuLRJWhyI0n4a99HH1VJCueRUPJ05g3XkPsI9eiu8YA2GkmGjIMJZFBQoPEhpUbVR8hcoNeG+yoImUpz2DH2/fjEd0HIo9nxjDCeBC7q4F6ACkFwP3RSZhJAiA2A9Ef2OCkrLYNeCyOJnfpYJaZkmxm1llnTvk8M5c022O5AkHAWHOOlIxM1BUpbwBdPqKWl2HMsoMiq2cmmqUh08QTgqBFZe0lY6qjuoFSaqUeIRATQMNsrf4ApsTlqMwzyQGjAg+TY1TZAgEbAS03KhumxJVKSUVYFSGkR5yq1Wcpzq91mQKSqJiQzOqyXOUVYT4sSgoSFgQWJFx4bpNjWEpQgmlxxaD6Q0ovWBJiLhZyYjwz0mb+ToPWA5jKcgBmnPUZmL6SioVsjKUSgkAtrkgpGsTUlQoP+kAoIEpSQ543sLygCFPjjmC8Ll8y/jOoBqDKhQDPlCPkSaS+ADOjD+L+2ESsS6hAryxs/VLxzjI8f8gxWdXfhaTjAwp8EI7Iejiguh6s3VaIWaZkTDJmSunBNDMVBAeQVA2cBvBpciPmmbJCJQb7sN8GtPRDwP4kSxJGWzIlPlTpkBgS5QvLSKIzMN1UiggDyagSpYYxUTV0SOIVEZcrpNQYXYaoMUj2EJzy2pE4GCMeBbkC+CTjTR8Dfa4qdwj5xPB6UPESBrz0WuD1o8IoykyCoACTotMw37Id720/Kp0eAhd1dmCsuIUZcQaG0j86TvPv/aGvdD6/5vMMzI/bo8pDOFbN+fhNbDY2Fp1rhQ4g7WgQU037QSD90B9ycawbONMPvLmuSgwaWbbFcc0yp/v0eeLnMFF/GATB9Gzg/GNpBX1JWOpBkEpFD1UDnHdU81ABQ9BLdQhLcGaaszFDiByWVxVK/EQhFCozk/HJv+vz5BqN1WdiUnwBxsYVYWwcibQSTLSUyXjmmKdaY1rMdjxg2IiPdhaLv4LEJ6iCxjj0MD6hjhkSt9CXKx/YRYPPsaPGRymFovBg6Yl4S5C0o4nrigOYHJeItXkdqA6o2DUAyKvlmnMQc0g0xqgyIM7v0bGHMMakyFOSjywpIRlGBQ8VEzTCnU4C0aC8caR8i+oJIVCzRK1CNQvXCBIMjAHLclj2NCGWr1PzcALJM0uBqEpYTsWxRh+e6edLePIxzVCEaVR30KcnLhcRcSy/IyGaL2OW14sxJ6E3OZalJ0qBxhIYkphUk1CVQsJTlEjGTCH4ZO5TPRKfL2upIjdCHjAhPxGukV9m47ihMfLXHf8UXgz0KQaD45/Xn9d0/RfJ+Hx7hlxjNV/8Yh6qTEQvEBvquS/3xfqv+CrOA3Vj+vWUG+GsMQHDhcxxNyiNJ4CgIZ7PehRTxv8G2uCbsciyBiccndKhpd7lwrbPE6ANuQW33j0ZxbbTqGruQ5n9rJS5UJZOVQKzkS6fIiUIEpjFrrA2CUCqrWNJQpuSs3t7xEeAYJLgkOQHgSGz1OIf4vNLNp8gQFQevnbJppIEYWZZZPxupRAgQJZOHm6WfXSjtladj4M+Dp52HKcSgyDFw9KaLjjq+1BjJYDolCwswSoz4vws3vBTHUBVi3T5ICFEvwN3O9w0ebSfCUnaCWy71HN8H8Gym/vvAQkKZ8MAbJ5eONydsElZh1K2ECjzPHk8ooSggWRdr4AoKjz4NyERXK0Sk7CRJ2MpvguUqLs6RebO4ydYqqBCxt0Hp69f9ksAShKh0tko2f2E5APnv3fC30mcSxdvHFvh3zlF+V0m8zMIfL5993lARCWGKBhsp2S81Dtr0OCogm7J0xg1chQGayOhaaMw/cHlKLIGccTRiwp3jwBjKaOpb5XyIyldCJll8tys9k6464Jy/FQSSOmKuwtOXiuWPgkJQYVJu1yDGttplfkWsNgNZ2OPUmYIYaVUBkI0uLsEwLsalIGllFd4ulBuPQNXY0BAKEuaapx9qLGrMcDPtnsHBOxKbD2dcPn6JIPOMVVtJxnih8NLBVNIyeFQCh2qOUgacH5xfAih4uU5n4G9QXUUIjCXOcgyCfGnUMazjIPNflbUOqK88ShllNPTBN2ShzFU0/CE+U846utHQ70bufuTcc1V34Y2+Dv4Iu04jnmBcu8AWCJWbVcKAJKLYdNTzhMqZViKw+MiyUci7ZiVaoAeIdpIpnHsu11npByD2X8C9XD5DOcwCQ9nPcmdU7B6T0t5Ds1OGUMSfvQWcTkHUFOrylZY6lPla0VVgyJSpazLTeVGM+ye+lC5Qz9uu+1ickN5W3BdUuQGf1dkFIkA+fkrPnLtrHO14ZSvDe5qK/TPPItrhl+FodrlGKRdjVkPLMWR2k7UNAHHSILV90j5jdPrl3Wh3H5GqdPcp9Hs4ph/EIOHDoE2aDg0GfdX49a7fo0X3/oMlQ0BHGWMG86g0teCCpbVcZyRkKQSzXYWHOdUHlU6z8DaQFJPlR+RMGUcqbIggeuo74etKQgqa8RT6CuedzheQoqETYBDChqODXY7Ut+t/dC0f0xuyP3rv+KX6tc4p3+TG18uaF+Z3Gg83YY178Sht/rVUAvXZ6UrCktS2CklSPNQkhxO+nAsRqB6MfrpyWFfAtj12PvpLEz6bw2jx1yHp5f8BN2+VfDbH8eA9VFFYpxXgoS9OsLGpFSHPIP+2qeFIGH72M1/noeFpnflBpwgcJrpEDLsQDOA7KNBaR8aqcsScPDM+gpUs5VdCxD9fBqmGdMwIS5bERSsPzeWYqyhSLLAVG+QkBBzSmO2gADKvgWc8UZdn4HIOAXUKNMmISC+Acwsh0gBZnMJ/KWu21JyvoZdVArL88AyGdVVJQdTYnMlw02gFmE6jomxZVIvz7KF8XF5IPARmf2yAqnjJyEjpEu8Il8IvKevKJbMK0GCxGLFEakvHxerpOIkVng+zLBL+QezwfocAZ8skRDgZCpARGw2IqUUQgFrHq8oECg5p68Iu1foD5z3IKBSQVQHBOWGIozhfuOUFwNjI5ljE7O/VGfQe0GV8kRa8jFm6V5MjC/BmDhm7wuk/p+kyyxjLuYakrFmRwU6+lj+TkMhdfPDG55uPzsXqLJ48E6oH+jtU6/hz/4edXPEbHxE7A4BXTxXllOMi0/HXg/Q1Q9s2V6NWfp0UetELN+LfbWQ7O3WlApMj0/Cb0wsDSrDNP1hJfEniKds35QpChyWUIx5TvlWcMywxGmc+RB+HbNPeWGQkKIfC0slzEq5QnUNySieN8cGy1aY/RdVh5BMF/wdwhlukm8Eqnwk4cbxx1KMiPhDmBe3A2uTTqAjFB+2QGJ0wrlnv4A41eeBN4znwTsx3kBQXvnxroOINO2QfdJ3heNpSnwePi0A2vxAbvFpzNXvlbKu3yfb4AVw2AmZX1FxGRgdw3goNQAJDiEqYvPE24aEkhAWRuVZQ0XSWP1BIX845jguRc0Qq7wpSNpQIUT1gZQ0EfjSCyNs9hubLSVlVP5QoUTlAYkTgnWCc+6PCgMqIcQzx1IgJAJ9KaJM+6R177odZegkAUYXq5ArN025+QUbjpt4V4WkkfyZf2c3jW4M4KNdWZhjSkJkXImUvbDEY+IKGm3uQEmjIs5InnE7BeAMgIxiYMGSRMznHKeHhjFP5gZVWyxJo08Q/UXEm4bqDnqgmPLw3zEZ531wqBqi74uQk4aDUj5CgpFjYepKlorQPyYH06l+or8GVUCxJEvoO5OLsSwNoo+HpRSRphxMNxwUEoNzk3GfIrRcqd8AACAASURBVD4pyi+FhBQ/6z5jESasPI6xJD64jhkKxAskUlcq+6afzXgqz2IPCjEiZS0rWHpzCFPiWD6SIedJNQ1JJ/rAcH36OhvXNvFH+ZrjX64pFxDOkSCvqAJQmxMPYOMX2bImnJ8fMosuJI+43nD7Jv/j+YezbiIJD0nzv+zPKguqlAAEX1QOXOzB4XPWobk6BzMm/BLakJvxsGUtyr0B1Doa0GivQur2bdC0m3HzPTORa2vFUZZiNPTA09gLm6tFsrEsQajwdIEgj5l2lpGwjINgipljRSgwu65UB3yO2XiXECz0kGgXsC/gljX9zKQ7KO8+I8THUdtp8RlQtfxtIVKiS/k5eFphd7SLmSmJCYJQUap4uwVIEIgSXFBWfp50YHtOHh9f6+hEraNPSccJOJynpOxFSlz4nK0NXqpIapuE8CG4I3lSLS06FeHETDi9L6guIWEjag76hoRq6KtIvnj64PT2CEh3UL5PNYQAZlVmQoApREddr+yLWVueB0sKbI5TcDLT7GgVkkPKcgii6SnhbEeV2y/kimR42UrW24JPt2yXtbUnoAhF+Y7iHLxoo9mb9CMKdUXwD6g1l9P1023JUn4RLnVx1veKWsXnqoevJhvjfvUtDNWGQdOuhKYNhzbsGmjabXja9D7owUHCSjr7uEhihQwU6XHCshp6QTja4aVaRUp9SBipc6W6gSVGVFEwpiSlCHTd9DFwKC8Exq7KRmVFkwB3EhVCSEi2v0NINQJJGW8i9ydoPwM3lUYOjpE2ud7h8cYxQqBPsojAMlz2RFKLJThhVYMoamjUKR1MuoXIEqKDyhKWLRCceoKocKouQuJvwTKFUBadc5HEAYGnmFpSuUHiyt0Kt6iHlDkox5DLXQ/dEzOlTeeDprdQXDeAFmcl/vyKCdqQ6/FfkdHiocBjpqkv/WI4vlkuJAbELLthiVVIJSXKF6qFnCR+OmUOi8Io5J9CEs9Frx2baqErfjccpy6lMiJ5SaBPolHKaqhmcraLUsTl6AQ3e0hZRADPco+TJJRIVFLhwvFA7xu2enY3qnV9ALhNylKoylCKEhKA0iXHoUxxhaAMlaeoNS9cnvTlHvl5brsNjsqT+K9f/RyDtMHQSGwMugxDNA0003zY/GfkuVWJD8kflq7Re4eqC5tXEVzsOHLWVYqlj0+BNkSDdunVQm4MHjwSl2pDoWkj8Mq6vShrBsrc3agQtRfLuNpE4UNFmHS7ctFfplXIXBKGnAu11tC8Dq2ZnPMcj8ephhLykuPky53vP3zdRd2DuMYo76WWvyY3/urL9ptdCvqP7jf+TW78o6j8/d++MrnRdPoMPnjHFCI3WJIS8tuwLRJyQzw02NWk6mGAj86lgGMp/IcfgGffLMz6tYZNaxfh1TeewmNP3IMWq0l1V3GyVSxLT54BqkNKDusiKXUZsCpiQ1rIhsiNgeql+PzP88+TG5RzR1j2IcuuwMSBomY88PQHmMs2jaZ0PLsuDx4AdS3AUtNmzLKkSovIadGJ4s8QqUvFbCPbWu7DDN70L6dx5yHM1qVgbmw6ImIzpXSBLR+n6RIRpctAxDJ6d+zHNMseqeOebdkn7UJnxtGz45CoQ2ayFeKyZCUXjyvC5PgsjNOnYI4lFQ+YU3B/zE48EPoMtrQkkCOwi4rejVkxe1QWdHkeWDIxx7gPkTEHhRQRDw3zXkyP2w36AUQt24K5MUly7CQv6PdBxcXs+L24P34PIqO3YZ4lDbPjdouknnX1bKs4K3YXFlhSxYMgInYn5hvS5XNZ8kAjwSjTfsyyZOC+ZYcEkEaa0jDTlIJIUxZmGA8pjwLDLsxkq9RY1u1TrbIPc/X7MFd3AFNX5EhrULaCZL17pDlF1BTzec6m/RhvOCTg6Dc6qljYcaRIMvbTYrZhTeIJyd6wD3lfb780MOBNT29QkRsDRKM9wECP6l/MPsaB7qCQHYEg8NEOehekKZJJl4Op8bkYHb8H+7wEtkBCwhHMM+4Wr41x5iQccLF3NLB9+2FM028XZQ9VA9NjczDblI4ow3bMM+1AlH4nZhj2ip8JDRdZPhEZvVtiNdaUgSmreR7089iPSD3b0qp2ntMsacorxLgTM83p4mVB7wbpZkMyYPnhkGRfdZ4Jd5RRniXKUJJkifydWX62BI39TMgNAm96ILJ1Fp2BGac+9MOPgGwE71S98Gaxj0oX/u7vRbC/Bxt27sd0Q4IoH0hGiaLJkoHPCoLyuqI8OxbGJiBKvwtVbSHVy94GREUnSCkYs/zTYw9inumg+HpQLTPfkIqo6BTMYOvSULcMljdN0e9AlCkBc80sD0vBbEOaaiWrKxDPCCmPYslJfBnui2bJziEZ49MMu8TvYp4hGXPZwlh/QIxOCXYjDZlCvsxeloh50Yny2XOXZ8ocJOBnqRb3y+sxV7cF63cdQ7cAW2kWru6yOa76AvAPMHb9kLHFYAVUXBlPxrgLQXy0MxPTn9siColJOnpXFGFc3EF8XBrEmRCBtGZbMR40rcFD8euwJasR6UVBPKrfjrlLd2CePgWR+kREmVNkLHFOkRjjxvk215KOqfokcLzMNqUKKTNep0qdZsbtUeuPiePrIKabM2QNmhydLB4yESvyMV63H3P1SVgQm4w50QcQEZ0lJq+j4w5hmuWgtGOOXLYDs0275bUsMaOnDef1XHMaZuuS8IAxVYg/Ki9GU1kWx246/MwkzDem4P5laZiv59p3EJMt6ZhjTsQc/TZw3nKNmR6zC1HGJMxbmSzeFrxOyoz4nyM3SBR+3fEf6ion15bzJOjvR59/AFu2p2PDp1mi3OE1JsGhMkmhL8y/utn6+y/Rb8pf/m/IDXWTTQAhpRQhQ0OCLZIbrdYsRI39MbRLbsEC8xqcqOuBx9eCU44K7PhsI7Qh38bNP5+HHGcbTja0wumoh7vWA6ezScDqMY8fFQ0BOHyn4HR5hfSg6oHAkKCP2V0CRqfzFNyeBvHkoOLDwdIDeja4mL3vhcPRDIe9Dk5KuwmCmDFn6UgDcNLTA7uLvgINKHf0oJpZdkczPK5T8Dla4aUHBQEdfQ/s7IbSK++lIqPe3QiHtV7Aa3VdH2yuU3A46lHnaRXQTGBWZWuHrcmPowS/jm443X7J1It3Rk0D6uuapZWi09OA6sYeVBCU0MTT1STna2dZiPeMZFnL6wfEC8HjboLP2QSPtw+VVipBmmF3N6PcRl8QCCFE9QlbNlLyLgQGSQsv/QBa5Zyp4vC4fPB5mlTnEGbJrY3w0HuhrgPHPd2o9QKVNkUK0dyxytWAbYkp5wGk+PT2q+8ofk/99cYFt19Ijj5/ED2BAfQFgW0794jZKlU4LCGizwNNZqnmMT4RiZEEhpdci7c3JotB5EmbD4uWvY4l0a/DYfeFYqUIITEZraOJo1/KK2rtLahzt8g48ngIdtvhbgxI+QtVNGxvSjKjwh3ASXdAnnfam+EVdUG7qDKoJmjyNsNp94i/B8dIrTsgZJDVUSfqAKpe7L6gKrew18Ptqofb0SAAnsCeJTz0dSHhR68ZliCx7IYtVuknQvLO4TsLez1l/I2wORtlzLAMiwqNcm8/ToqvQjPcjiZU2aniAU44gUpPUBlMhroOXaygUuTGhW5CJDdIqtHQssKtyDte87jF0zBC07Ao/m2UeQfgrirFnTePgDb0Zrz04QFU2ntE9SFzpa5J4sm4ktw46Twt8/g4WxnTKLS2AU2+Drid9GZpht3XDvpzsMMRSzHoPyFKLhIJBOCOZtS5muCx1cNlaxZlR7mrFRX1flTWnxOQ+1g+0SzzwmdvgYdlLc5TcDZ0SkwqfAOo8gEn3DT9JWHH8gySG/SaaD7PYLMsxSGmtyzDUEa7JEPZMSisNOO69WXJ3L99ncvVKKSQ7skF0EhCXDoK76/fLsfOtqhLli3Dg+Y3cKz5HHQiOVXbLD419AIieUjll62uHzZbPVpdhTA+Mw3a0MF43PQCHA2tqK1yYMZv7sMw7VLcG/Ec8rzn4FSDHy4vy9wahWwSPw43zXmbYXM3wOdthtfbgqraU0KyeTwDcLhovNyG6voOWVOplLHXBVBpUwTY357Xl//9QkkLVSH8HOnG5Ap7blC5Mfhvsghh841vyrfs//s8/01u/L9jxFd8ZXLDd7YV779rRlfty2ISylKU8Kbav9JIdDFAzwzrg+irfTTU6YQKj6UYsOnRXvsa3nptDmKf/CmCrhcQrKZqg+TGk8pPo/aZ894bNBiloSiVIbL/msWqLKVyKTa/8wAe0n+gykosRZgStwf7rX7JlB4scuEpw3siQ5+tX4cVH+xCCzOpZ4AYy2eYbdmGt/c1oWEA6CAgGQAazwB/XnsCD0UnYrJuO0o7FVFienUPJut3I/KF/SjvUsqQZS/lYqFpP36XaIULQDuAA0WnsNCQhinRu/HMuf3UUsbef84/1QXMNqZgrIFKhVS8ussBjx9oDQKBfuBEVQ+eNG3G/ZYkjF+Rgqx2oD0IrFi1H1E61tvvQ2Uf4BsAlq06gEctmYgwpOLd/Wfg6Ydk7QnGyqt68dTKPZiu2y3AKNWqjrUlqOT07QPArsw63G/4DJPMKXh7Xxfqu4DOANAGwNMN/H59MR5Y9jlmmXbiRAdwNgDoVu7FDF2ugMnj7QCl9s+8VgICpJo+oPFcdjr2xTzMX3YAU8y7cLQPaOkDjC8lY7IhEZPjU/CnnTbU+1WcuvuBo8d7EB23DXNMqdIBRHwTmLE2FQupMjMuEe+nHEOXvx/9ve2y4AX8IaDpDyLAwIXBZ08Ar7z+hsjKGQeClm5/HzYkZgnYpsmnlOoYMjF++T7scQK9fiA97Tjm65MxliTMy1lIswG9nUD6rmohnKYTkOn34rcJbvigYsksfEGNH4tWJomB5+xzoO74GaCzD9A/r4D82Lh9qOgGvOeusf7lAjwYk4L39zjh7FfXgeSCtwV4a/1RPGrYg5nP7sNMmrBGq1asUgrA1rShdr0kNEiyqE11bSERRN+YucbtWLfzGHoZC0l3cVAFESTRExyQ9lBsEcXWWtwYN7+fgRxAfyAonomf7KBaJk0Ra3FFuE9/EGPiD+LTkn5RwZwsrcVC3VpsL2oXgO9rAR5bkYRI834h0KYb0/FRahMauhXxwbFUdqIdMSu3YK5lt4z7sSuz8FJqs6iqWgOqBITqmTMBwPj6XsxZxrIRZUpJlQEVAwTqu62Q2HOfNHzk2Ek85MVc0zZELk/HRH0y1h7qhLtL7ZMA9kRFJ5ZYtorvDo11afzKLh8R+r2YZ9yOvyQcBecCtT7B3j6gj+aRivDpG/Aj0O9XsWQtil/FjWRYd4jg+HhXAe4375bSJHbboGpn8opUlLVB3YxvO4wFhh2I0HPdSMOM5fswyZyGj4uCcv48F859rjkcw+U2YE78XkzSpYofiI/zh68B14ZOLDV8jAdM9Js4iKPtKh7RrxZi9tJ9mGNKwfE2CKmy9NU9+LVpF1alNct7SdTlFvTjIV0SJpr3YMmHR1AbUGtauQ94IHozoixUhe3HX/b5UNurrh9VLVVVASwzfY5Zy9JEETfVkoRPSjpFiXKWa9dZwLLyEyTktMp6wHIdEgM85pYBoKIOeDx2HRytat7EvFyAWc+FiLwvWYby96UqypOFipKvO/57gwAzyFRxcD4QbG3bno5NX+TI9VDKDY4MVb7CB9loMCoLzpf7Yv1XfBWHKw0kJevLzO9X3NRNsAIHzNhxXyQBROLt7pYyg9PVhzBv4k+gDRmFh0zvCmh2e7xosh9H2o5t0Abdhut/Nhe5BGD19Xj7eTO+e+lQDNYugTb0Blz/y1lYl5QDt7sGyVvXhTL6I6ENuhraoBuhX/UxKmzd8FSdxKzxv8IgyZgOxdDBV0AbdiueXv05jnuAFrcdb78Qg+uuGCYO/pp2NW764QSsSz6JCoLUyjJ875YboV1xL/Yd64Ojrgnuqkrced0PcNmgm3DoRBWOeU/h1mt/jqsG3YGikz7YvPVorCjAD2+4FtrIH+PASWbvfThSkIvJ943FcG2obIOGjoJ22Q+wu7JHyhNs9nacJOlR14a6Oh98tgoYn3oQlzJrO+R6XP/j0Sg6UoZnlzyCSzVNygeGDBkCbchIaJd8D7+IeByuqmP4wajLcc9dv8QnH+/E1dcQmA7Ft34yExtSbTjWSPBXjzpHKX7//NO4ZcSlGEoANnQkxi9YggJrN2rq++CoOo7bb70J2uU/RlZpE864rZj8m19AG3YTHol/H9XOAKzWDiGSxDTS1YzPd+5BL9lkqjA55wL87rl4C8p3Eb+Pgv6AfD9R1UGlYY8f2L5rv+oiQ5WKKA5Ow1fvgKfmGO64YhSGayPw+vok5Ht7cZIdXnyqfSnBpH5RFK7WNJUZ14ZiiGTLr8RPIo0o9EE8C95YacCokUMxeLDKnkcufBoFtg7Ql6SxphJ3XH8TtBE/wUFeL/o01Njw7Wt+hBGX3omMk/U4XteAtW/E40qOpaE34AHTezjuViqnlO1rceO16u//MXWJKG089U1w1Zbhjy8ZcdPIkWqMDh2OKQ8tQW4VDWi70dBYB3dNGXRPLcZQjaUHl+H2n/0KeSeP4KElj2LI0Esk889SEWbqtWHfx69nPwdHxTHcccMoDL/ybhw60odyD1DhCooyR4gdUR6o9sME7syuS+cdlk25uqUkhUQgDXjF1Nfjh9tWB8tjY3GNpmGJ7nkcdbXjySUPQRus4db/nImDtUEcc/XB03Baxs9vVz2NG0ders5r0EhMvv8p5No7ZYxRCeLzNuHt3z6P4Ryrl1BxMxJDtFtx+eU/we4KL0rOKOKJHhQsv/G6m+E7kY2FE+7GVZqGQVTnXHoTtMvuwJMrPsEJ9wDcdS64a0vw5vPLcf2Iy+XYtKHDMel+HXIre1DphaiKxNBYOrcocoMEkmLe+vGd274lSg6q01haxbiIsoCdlkJeKYrcCIP8r/bIsrvWykL84LpLoA2+FqvXpMDuPVeF7+iSEq5aXwNqGxtxotaG7153J35916+QsHEjRl15OTRtGL53zxh8mHwc1oZ+nLYVwbg4Atpll2KhaTVsDafhsHswdcxEDNJG4rdr9+KYtx8J276QOIsyhMqmYT+EcdUG2OtPocZ6DBFj75E1Y/jgy6Bp10EbdAcMz2/Esfp+HPF14KS3RQyZPVTThM1oheD5auceJoVE0cX9OP1wOPshLXqdZy9SbgyT6xHOJygT77CE9l/xW/Wrn5PVav/qb/oGvsNmc3yls9Z8Z7rw3p/j0Gl9UbwxaADKchTx22DrVyo5aPrJFq/2h6UtrHQ7sT6l/l79CAJWM9a9GYXoh78Pf60FsD+JAZqKUpVR84wQGdI1xfmQmIvyZ/HeCBuLssyl4hlse5vkxjppRUqJP8mNTHe/3IATCHGjLJxlKgSlJCAamwDd8s8w27wVRzoVqOdtK8Ehb3jPNACxlh2YvyIRR7uA1nM4Z+UrWzBL/wU+KWwXqflZALpVB7EwOhlbS+rFl4A4qOk0sDg+SUoqNpd2oaYD6OuBOBUTVEVY9uDVFBfqQsfCz+XNdZ//XBXPuXrF+dEfYeqq7SgNAF3n7rJfXPEFFur3igS+ulMBD/NL+/Hgc0nYltcn3iIEEzxPf4go8fAYVuzCnLjtOEHiInRLzuMj+KBp3u83FCIiLhnF3Yp8ISDkvQdLG0jwPGv+HAviE1DeCvT2Ai+s2o4H9PsRZUhFbaeKZ/RL+XjImILargGJsWn1Hjwem4otJZ1yfv5zYPqFl7cgMj4BLyW5BKzR0yB8zvyh1g48qNsmZpbM7LKMZ5KxSLozzDAn4N3EMsmiDgQ6EQz0yU0PwTk3gnfeIPEFr73yBpavXo34Vavk773d1CwMiOnodP0uVTYUmyfGlxNW7EeaXZFKSTuLxNuDyoKxK/ZhtxMY8AMpW45jgS5dfBreTKmX8+E1Z/wYz7MEfz7gkdiNmGvcBFs7EOgEXlqdJF1Kpi9PRU2nAnpxL2bhoaWJqOpQY5HXQXBTP1DXyFgn4UHdAUyPpiGuKj2hCkkUBzQklUw1yQ3VmlTakhpzxcySypo5xq1CbnT3hfwEWJ7T1w8SQX6JVQCBQEB+pxKfN5B+Anpei1610TiTHWfYjpTlEixDGrciCxvye2VOEOBzDtF/4+yZAbz11lbMi0nADEumZO0/LgwIOdYTVPOJc40g0XcaeCQ+ETPi9+K+5XvwYUkv2kIpcXp/kKggRxW3+jPcH5uEmaYMTGa3I8tBOX+qCU62qzhyf/zC49t5DVZtOIJphh34ojQoZTIkDLg/Zvq4z+YWxjYRM3Qk3JQ5bqT5IOYYErA28STa+oEeMly03Ojrh58ch38AvcEA/ME+IcgGJKYky6gWAnh+3YEBbNiRK115WPJFZcNkyyHMf3WfkJyBHuClVVtFeUUjWW4sKxu3Mg9rSgA3Yxg6j3ANjNUJROq24fNStU7x/MLrFStnWk4DT5gPYIF5D6rC82/1QTwcsxs7ctqEUOjsAcyvJmDyCyl4r7hHYsSL0NoELIv7HJHxO7C+rAs2Ehh+oMYxgMee2yjX/aN85VPEMhp+Lj+fIKT5NPBkfIp0k9lcdEZITMaZY5hY3+4CknPbZGxw7eA16gyqkq8KJ/Ck7gPUtffJuhK3ehcei94p8y3KkIzpxv1SxqKUSCylU5uYHlNtc954NGxAqh6lzOtrjn/OCaq+uv0B8Z/x+4Po6wtg6/Y0ITe4NvLcQuL5CxOVi7RcLK5e39x//1fkBkkR8ZRgltRzWsgNZqyZyW2tzcGs0XdCG3o1tGG3QRt0JQZrg3B5CLRrg27HjT+fj1x7C07abbj7uktwvaZhGEHe4KuhDfkebrs3ApXVJ5GyY6NI6YdoQzFIgPo10C67G58ll6KhohQ/vXFwSA7O5wdDG8Tnf46P91TCc7IMP7lBk/drgwggh0upzC2/WIii6jZ4qwpx100joF3xc6Qf6YHDUwdn5XHcddWPcO1ld2BfVQ1ynR58/9pf4OZB30fJkRrYPVZYnpiJK3isV/0K6ce7Jbt0O/ejDcYgbZg8N4QlFqP+C8nlAzhp7xZQQc8B+kTUu61Y9vg8ASyUsWtDroV2yXWYNDMSSxY/KO9nrOSYGcNLvof/mvE4GioKcc91QzBII4gZqeTsw/i6G6GN/CkOHG+U+vxnnrpflBCKJBmsXnfJZbjhnggUV5+Gt7oE37/hCmgj7kbO4VM4lrkbN16pQbvmLqSUs91nPzwumh62SamOo7EdmxJSESCxQaJYNqWaYhJCbQEhNUhsUFFF8p3fXbyH4Pfa5q1p4jfC8iApj6k7BZ/nOA5np+KW4bfi8qF3Yc+JZhScGhCFgJTHuNrgdPlgeWqugHKejwJ4w6ANvRE/i4pBiQ9YvPgpAXeqLEDDICE4hsv50u/FdzgX99x4DbQr7kH6URptevDM4scxXLsBl172Q+w+bkd5cwNMj87CtYz7kKtx4y9noIBZbu9pLHlyOn50x9W4bMT3MDZiqXhfOOqceO6phQpUytgdquI8fDhu+VkUymo74XMeR8yiaRhOAkvG3qUgWP/NjOl4IvpZIeU45gcPHgxt8JXQhv8A/zltERorS3D3qOG49LLbkHm4HSdY4lA3AKqElBpBgVKWW/wducESBNsZ6ZwhBpJulmR1o97ZgJWPT8B1PD8eyyWjhDz4/j0/xqdZNpQ2836oHQ5nLZ57KgqXDVIEm5AQg4ZAGzYC1/9sCrKt3VIiQnWQ/vGZuIax5qaxnOJ2XDrkbuyvqEduYxtONPiVcbCzV5GeJ/fiF9drsg6wjEMbxDF8C7Thv8CnqcfhcZUj9smZEtNLZF5o0IYNERLhjnunI7+8DRX0BKnzh5QboU4/YXJjIIDv3HbLeXKDxAYJjfMk7P8BueF1+lC5bwu+O0KDNvJOpFcN4LhjADXOHtgae1HpbYCjvgbWqjL85Lrv4mrtErV+DVbxFG+Nq36BjBOn0Oo8jJhHJkAbfrm6HkM4r9V6FqN7Hse9wMm6IJK3fixrwiUSZ77mdmiXfB9bU9JQW3sEP7r58tCawxIZlrd8B9olP8JHaUdwtMmPivpW2OvPStcWdk7i2v31CR5FGHEO04CYhq8kN/hdEFZKUtEi92Sh+72/Ijcky/DN/f4Nn/m/lRvhSPzvj1+Z3Khv8eP9d1aip3Y1YGX7VpIYj18gN6qfBsQ3g54Zj4kHR8C+SFrEiq+G7VH0VMdi3e9nYdkjIXKDqo0qEiI0C6V3xyJFitgfw4D9IcDGjUoQEiAsd1kk5EbCOwvwoOF9qd8mKJ5h2otDLgW2CUS7QllKEhzMhPKmnTfsuvgvMMu4A/Hrq7BsxVY88dyfoH99PZxnAX83sHp1kpQfHCawOgfAnn9pA9ZuKVIgIrQf06ocPBKTKow0gV9BZZ08/9q6I3jUuAW+VjL3bTjV2glfO7AgPkXk2ifOKrD25w93YknMKzC9tgbHXD2SoTC/tBWz47agrEOBhJdeWYeHoz/Fg4ZNcHb2CfB47qWDWLY6B2d6lOJkzfZKRMVuwuLf7YOLqoUAsGvXcSyI34yjbUBTK6A3voGnLG+i1NYt5MYf1tHXIBmWLxqwyLgZi6PfgemNj2E/TUAMxK3cgoXGnahoVYqE1S+twyPRG/Cw8SM42gNynste4PmnwNqhSBf9yzuxbnOtPEeyhcA5fvVWzFz5OYqZVacR49rNeDr6dVheXCsZO2bwY19mCctesP2qdJUxFEi7x2n6LfgguVwy7FRh+NGLrmCXgEx6btBQtC/QK6CdGWq9ZbmATyE+/P0I9A2AigS2P2V9P8sS2EJyXPxepDtVWUpSUhlmx2yT8qPxK/aIooOgLWnHcWmZGrHiII71KmXK2+vS8EzsH6B/7SMc8wblpiv+hU/xcNwXqGgB+nuA11Z/goXRH2OhZRMcXSqDbX4lGwuWpmL1R8fwpW2jKwAAIABJREFU6KrP8KDxXZheW4v61nZ0nVPUmF/eg4W6Q2KwOiFkIkoiI8KQKxuP+4I/Ac8hWzZ2NZlsPohZpi1Yu+so2kM3jf1E4QNAZ1efxIpgvauvV66rqDeCSvXi71VjPdgHbEzIQaRlN8YYVecXEirs/rKpoF9KWGhESnUO5xF/TkkqwMPP7cRs/QEsfH0/rCQWgsAnm0ukQ8ijb6TDE1RA+dNddXhAt1WMNj8u6ZFyoJSkIiw0r0c1yb9ekkKbMc+wBVNMOzDd+BlmGjdjjjEd8w07YW0F3OeIoWXL/4BnjK/jcI1P5sHKDRVY9FoGGvxqXn+4uRKPmr7A4t/ulPIzklSJO6sQpU+SEi2SZyxLmWfehg8Sj6D1HGlHRYsQPSzRCShipKe/Hz0Bv6heWApFTMuxpEpWFMmxYWeelFeRUKUJ6Dj9XkR/UCbkT/DcQH9x1ReYp9ur2sMaC4U0oqHvOHpQrNyN1xIrJa5lRW48EvuJtOR94ncHRVVxth9Yv+0Y5pkTsPjVPWgIAK0DwBdpp7Bg2UbUdCmSaemLSVi7xaEIHdpHBADz6k2YYd6KVIdaY04c88nxv79uD+bFfYLSHqC0sVfWo9MNgM6wCU+/sR/H/erart1xFHPMCXj05VTUh67fpj11iH15B5q7FGnxhw9z8bh+M95cV460ImCOLl3KzP6YeFJIjsyiNix6diMW6lKwwLIdlSGST8qASGgFgd05Htyv34JZ5gMYvzQDUy2HMSmuFKPZFSouX/xHSHKEPWeUj5Ay1P1nx79SdgWELO3t7ZbrvDlhNz7dlivHRn9Z9S9MaJCy4Sa0bPjJb+QjQ/NPe27QRJMmfZTI17UoQ8O6TlS5g3A7W9BWk415Y++CdskVokpgVnr4oCECaoZpg+Tm/JZ7FyCnth2Vvmbs3Po+6soPocldjvyMfNwy6lcYPvxuZBx1osLbBK/LLYaTzppi/PK+/4Q24gf4JO0wGssP4+fXD8fdP74Xx2vdcDhOYPTEsdBG/Bif7q5Evd2F3Vs+RIX1MKx1lTicux/fvuE2aCPvRdbh00KO3DVqGC678g4cKvXBXueEvaYS373iXlw1/Cc4UO1Asaced157D76l3YSqo2X43ZsqW62RYBjxS2Qda0PSlo0YNljD1T//NfZW2NFYdRR3XUvlxi+x99i5fJAnICUnNIR0uOtx+FAibrmCkvZvyXnQLHDtZ1vwpO55uOqa0Wo7jr+8/ryoNh6O+wOO1gVFjn7qaC7uuYEZ7VF40Pg6jjorkJmTjFuvHolLtKH40/ufIj2vHJeOuAXDLrkJf16bIv4ah7OTccPVJDluxuvvJ6C+Ih/33HgZhg3/FvJLfVj6+KMYMljDT2c8ifwGSCkEM9Gs1SdxxRKKrTuT5fuSgkESyPzX1dWlSPdAAH09vUJu9Af94q8VYCIjGJA1l0mnLTtSxGOEvif0GKHBZavrOHZ/tg7DtBsw5NJ7sK/iNIob/ThBE1mawdK3wtOFelcLTrls+Mtrz2H4YA1LzG/isGtA5P6HsnNwxdU3S0nLex9tF2BblpWGay8fDm3w7fjjB7tx6kQpfnLd5Rh89Y9x4Ngp/O7N10KZ8Fsx5LIfIb2qEkcanYj8zWTcqI3A/PsfhDbycmzcsxelXjeuvG0UfjN2DH5w03/il9+bgOrqamTmHcLIq26CNuQ6/GX9TrC8qDQrEdddQTB+O17/SzKO5abiuks1aFfcjA17ymBzNeGjjzdjseE16Vpxuq4Wf3ptFbSh1+Jhyzs4eo5MrvN04vTxfPziGk1AvniQDBoFbeQdePbFTSiro5cD26uyBehF5IYYRCowT6BJRZWUj9TRj6QTza5GLH9onJCIArCHjRKiaMjQS/HqhgyU1PGz7SjNScVVV5CUvB5vr98tJUTFuakYdc1QUUWt/mAPytlO1OlC3BPzROnyhzVv4bjVhzuu+g9cp92FomN2nPA1oabxLMo9p1HVwBKwBpw6noV7bxiGH//0P3C0ugFehwMTxk+FNvxufJJ8GIWZKbh5JMmpG/Hu2jQxqczPy8R1IwZj0KAhWP1+GkrqCfj9YBmR8jZpk5IzNSL9Qm6wrIbgnWUT4s8TUqfxbwLK/4myFJb3ZHzxrlL4XHEPUk8Ax1kyQ+Nh+gN5G2H3VcNjPY67r7gRV2pX4DHLG8iyenAkJw03jSCZeRte/zAFZ+ylMD0+Fdowkjwkmy4XQnMIybDBw/CQcQ1O1ANOqw2n3cfhcp9Epa0WP/3/ImTtSNi7D7U2K+66+lv47zt+jqpqO8odDRgzcQG0Ibfj85QyUahxvtEYl4QhYxZWYHAMfZ1NVEIkjuif8neeGwgZiv5PX6/8Tv73P6u1JhSE/ykeobL9875h4d//BWLHyaomrJxM+Nfw48VnKORG6Il/9PzFr+XPGsmNNe+sRG/NC0BtiNxg+1YpHaE3xrNAFQkOZQjab31cDEMDDqo7aDb6EPxWHf782lToF92Fvpo4wP4McJLExeJzd0+qzCVoUyTH+c4p8t6/Jje2vbNAJIDsJKHIjX1Ir/ULCMssdOCZmD9hoW4d5hjWYtXa3QKKfE1AtPlTzNJtxcoNVbA2AgQU7LDCcoteZl5f2Y7Zhi043KHUHu+8vxWt3UCTZJGDOEtQujofT+r3oLZNZbX/kpAtn7unLIAX39oHfpEnJ2WguSsgN/3P/DYbxnfKJMPdQSA1oMwaCRi50bjx7Y8KhNwoJ3HBDCkz4QMKJFKhwYzvc6/m4vl3jgsZcvrsAJ5+PglRlv0Ya0zFpmK/1JMX51VjgXGDlJVIdwxmskMKlt17q/CUfg1mvZCK6A1VqGpR2XZm5Zm5DZ7Dxqtf2oJ5+h0o71CkBJUdzNg29yvQRF8B44v5eCJ2Nxwd6vjeWLNbSlHqScwwS9MBrH5lK2I/zJTyHLmnCZWl8HO4P57T6+vLMWsZ/SqyxZeEhoWRcTmIMmzBmsRjkmFnrDr93egd8IvremdfUHwkuvydkuHp7htAtMGsqjJYstIXFHKFrR//ltyYFL8P+0huBIDExBLxFpjC9peWVOx3qYx04s6j4qnx1AeVkmnnsTKOXSEQyOtFDuH9jwowM+Yj1PbQr0GpPljuwPMLZ8GjX9iPR6LT8eKaElHCcJyRKCDRRsCnf3EPop7dLQayBMskM0hsROqypRSIpSjSzYftTc2q04hkuy8iNwjWSW4IsdPDm0U/fvfmW3j1d3/ACy+9iNd+9waef2E1DEYzlsVEC6DrZO0BjVh7gtiYkIXpxiSMY3ccSyHo7zBtZQE+LQzKtSwuqsRj5nXYmd+k1Ct9QPzLGZgfnQL9hyVCbpBEM67chEjTHlFzfJ7fKPMts7BXCLqo5QnYz7j7gQ/X70ekcZMop0iyvLLqC/xxhx1csqlsYIxKPMqw1BOag1RdcZ5yDqSVuDHfvBOmdwvleLxNQcQ+n4I50bswKT4RGwrPirKgOLcB883J4qlCg1/6dFCBtS7pmJhH9vX1SaaQ2fuXX/sDXvrtH/DyG2/gpddexcrnX0ScZSUMOrOoGFjiw4w/b87Xbc3EDFMyxluKRJUxZXkmYtaUyXUlWfTiqs/F/2aaKRRPPcubaDibg/9akY1XUk+hJwAU5rkx35SKCYZ0xK4tkfN2n4YQrjP06eI1klDok7F0oLAPS0yfiBqM69Tr6/eiiSoMzrcuoK8TWPXqZ5i/PAGHu4BTAeCjjelCRuWW1GL1unRRIK3fdxJ1HUCgA3jlpa2wvH9QFCeu08Bzy7+QErhJlnRsKfbJupRS2oFX31P7OX0GeG5FCmY/m4LZy1LEV2dq9EHMtBzAb5OsoqDJLA7iiaUJiIo9gGmGRFQH1fpGwpPzmBQB1R17i7uwQJ+EKLb1jS2StrX09qCxKruvSEtr8UpRxKQqUVFlKV93/BsNcYiNNojiq7u7U0pPSJR+nrAHH205JGNJTEf5TShZIrJGJDaUwufiL9W//WL8JvzOsPxfkRviSeE9rVpRCrnhh8fZjLaqDMwfdye0ISOwOP6P8nn1bh+a7eXYtY1lKd/FzT97AAXVLahpaMbGTWvwi5/dJoDzMo2Z3Rtx5fB7kXGiGWXeM3jz92/h8iEaJHM5TMMDy9/FiQag6UQJ7rmaJSdXS3ZXShIIfletk6xno9OLrRvfx533/hDaJdoFRcSIXyD7aDsayo/gpzdcGlJBjII2lBnowRihfRtXDGFGvxz5DivuuOZOfG/wjUhJ2IKrrhmKu77//7P33uFRXVfX+GCKccMFt7gmTpw4jksSJ2/yvrHBdAlJFIMbxcaNYkCaKgkbm7jFJXFisOkY24CNMUI0SQhEk0AFia4uTdeod2k0GtX1sfa5V+DEyRf7/f3xS/Lpec4zozt37j1nnzJ3r7P22rfhsituEoZI+lk/cg4m48pLDLjmgd8iudCutAyGDkW/K36DfaeBPGcHnD4Kkyo9jINbVoj2wQ0/C8cR17k9IW8VXFqKTmpiNDrO4MO3F8EwcCieiF2KXF8QXocPTWczcfdQMk3uxPLEk8ivroTdeRoT//s+Cdv4YPlqfBZ/EAbDLfjRvRNwrLhHnJdGRyaMz4SLtsKz1vdQU3Qcdw0x4CLu8l50vTi5P/nZfdh1tlbADYZBKDHLr4Mb/O1kiAnnGxlz77z7R/zh7XexZMlrePvtd7F48WKYzWYsWPAiunq60RYIKpZeRw82b00QbRJmxJFQAUc5Gp15SNq4DoNYj3MhGcln65Fd0Y3i6g6cKakV0VQKcjJExlPiwep3XsTF/Qx4zPhHnKoEyr0OJGxeL/0nO/sFKtVrMxkTs+jg3Y5nje+j8lQ67rtmEPpdfAM+T8rGpUOuxF0//AmGXnIPBg66E/sKz+J4WSluu+pu3Drwdny2aqmwMGbHLMTy+K0wXHoFXv/LJ7jtsp/hlgG34dTxdGzY8pkwZn583yPIKKS+QxUaXRkwzpoEMpNmRX2A5C9XC6B346/Csd8FaX+Zt0aykZCF0eDIl9AO0aaJXY1cN+AtqUZrbgZ+frVB5kO//leqTBr9r4Lhknswzboa1L2gfgMBqD7mBlOclvklI4diKlCIVqX/pKhqud2D2JkjMdRgwBzjIsk8M2/WdMWEGfJzpJxths+dh11frJD5dMf9k3G0tEdCyqpdGZg/K1yyH82wrkAu9U1cLkT8z4MYOngQNidtx/FiF3405Fe4yfATnDpRgsXvvANDfzJsGG4zFCPDpqIpPxv3XD1ImFwM6WBIyyCDAS8uWY/cSmDPV2tkjt5530RkFELmS1WZA6anIuTc6dEf4YgGblC3RTnqBFmVmCXXeTI3JLOLABtBAYBUylzl1Ctw47s59QQCCG4c+uIDBW4MuR9JZ4CTvm6U1LTjjNMHZ1UlHOUlKD6bjV8NvQ1XG67Bh4mncay+C5WFmZg67BeiOfTa8m1ochyH7enxYo9nLH+UNK5erxeffPwBDAMHwjD4XqzdWYJKXy2Wvv2KYshIGNvlmGdajFNlPpwudeGuq+/EtZxDzLgycBAIvMbEvidhPKc9EEFeZo8S0eLydg3g+e426AM3CCB5CXQ39gFM/H35e9lSlHP695z5/4RfX72NPVDgBm1xYTn/uX5cZ73or+q4ft6/6KsaCH2V18cFX7/Wvl5Nc0N90Hf+P3ojYSnLl0ajvWSxYm1oYSlkZ3Q5ngMc89BD5gZDU5gW1vkMCGz0OJ4FnM8Crlnoshux6t0QRD39Q3SVvIyePJ7LcBaVQpb6Gt2lc6QorY1nBPQQ4IMipQxxyZ+HzUsfx6PWD2W372EKcUYn44BX7WweyqzDs9wVNe/EONtORK7OEMepppFhJ59g9lu74ehVDnZNh3Ko6OAzDt76ynpMtGzE6XblhHurm0VsbunHiXA0t4iDZV18FM+8uF10KpzBDrzwykYU1AMlLcDuo17ZqXjltTVIL1JhK/PfOoxFf8kSp5bUZ8bw+zuB+h718F95bpwu+eQsQmK24iSZDiIOqQEPPQpkIftkzmsHEfOnHHnkpn7I85Y4TIpMEg2NDcf84kAcyyrCtOiPkdes2sM26Q43H97jdmVh+h++RIEGMNDxoNgqnW5GesQsXoMpsXHIblIhL0Lz71L1pFPO822vpmL6nO2ys06Hs7yuV7Q73v80FU56/+cylrwcswrzV+0V55fgAJ9WCLLQeeUr7/f62lJMiNyLcJOKx2d62pCFKZhq3YgPvzwidg8E1M56sKMH/mCXOJmBYCu6ERQKKx+WZj3/AvzBdnR0tKOTJdj1NeYGnSPu+o6L3o/9dhWCtDP+GCYu2CWZcUYvSkFSCdATAHZ+lSsCrvPWFomD10oQgNosdNTO6Z6weQR4lqw6jQmLtyGHu9oaMNSgtVEHixa+ngLjK6nSnwxxquhV45OACR32qCUpmEKxWi0dsAI3UhFmPCyFx/WUsHzVU/ZSm4QZdxiWspIgUAfQ2dGrQizaOtB+bot8yRt/wOJXX0GUyYgooxnzXlygHhw7ghJ+QYo+WR2fbj8KhgpQm4QZYJiNZ5h1nwLLqI+Sacfj87/Eo5adKNVCuTZsL8YM4+dYsPKopFj2MAuRbR0mRCWIcGxidrUAdAcyO/HEvM/w3Fu74CDNmMygxesxMXaTpJRtawNeXfwZ/rjVKeNERH/JhHIAM01xcDQA1IyhrTj2WDiW1+0ux6sfpglAVO/vxvzYOEyJ3I3QmF3YlN2OQCeQkVGDiQviVZrR6FOSuYbMBMattjAkp6NbwMD2QJcwNxYveRPRL72MRS+/hPkLjJgzez46gz1oa+U460agvUPCnj6LI/i2U1JHP2hJxwjbQTzx1kEBDxjpsjX+BB41xwlQMMpCId79GB+1G9Qm+V3MAfwhsV7Al+yjbhHvpPBv1NrjAg5UNQHzrBuEOTQucjvij/lkvdl/rAezIj+BUwtP8zU1ScaX9z4+AE+zYmzFvvopJlk3IbsFINs25pWVcDd3wdXaiYT0Qhm7897dJbbtPoesLVm8FuYPdsl9a87ZeYHlE4yPTsUwy158eaxK5uj2k91Y9ME+WRfoKEybuwXTTIfwuC0REVHxiKCIrCUB78TnCzi8N70DTy3cJSK8ZAMVaylxLW/uwPT5n+DTPcXSf94mYLYtTsLdqDczMjIdoYtOSh8xe5MKw9LTB3PcK2CDx2UOfIfx/+K8KHRR76Vdrb+B7m60dPbgix378PGWQzKHyUzSQQyVY4gL1wXPEf/o1/Hf/DOahuCG/oD6bV/5gK+cBb84PnncEWRsu9CUA/C5KtBckoIJBDcGXIdHLctFrJNimLWO09ixZaPsbN/0wCM4UVSCtMzDuPTKoRKPzrACOjsDDN/DpYN+hoMnncirbMDit/50fkeTYRiX/hjrduSgLi8b9w9lCsXrxZGldsGAi/rDcPGdeG3FbmQfTsX1F3MXdDAMF10sgMIghq5c+gBSTvlRUXgWPx3K2PkrBBwxDBiEiwyDcYXhVlxuuB1H7AU4UVaAu669HdcahuCen/8OhsGXYNsX6/CDW74Pw+W/wuFTQVSW+DDhof+Sh3oCJP0YAsN7XvZbJB4HSsoJFrTILme5uxL7NywVJ+634QuRWaacXperEnllFI7sRK2nEO+9HQvDoBswNXopcinc6HaiMTcTdw0dAsPgH2BNch5OeatBZ+jRhx4SHYOla9dg1bZdMBhuxm0/DUVmSSeKfE2ot2cj8tlHYLj0dkyPeR/u3BO47yZmI2FmErWDP+Diy7Ey6Swyqrgz3qN2xZlhRZzmOmzaliAgeVtnr7Ar/e3dYFny+ttY/MrriDLaEGW0Yt6LkZSLQltHt4QJMwywtR34Mn6fjDuVrYXtaUCFx4FT6Sm4fsBFGCjZIfZKpqqz3mY4KxtQVFoDb3lA0ulWlVXiozcXYkA/A2a+tApZXqDW60DSpjW4yHAlfnB3KNJLOiQzRVXJCUmxabj4ZjxlfBONRdn49bX9MGTgpfjhz34Lw8XXYNOW/fj+lQ/g2oF34OCJbJxw2PH9636D/7r9QTiy9+OO6w24/76fYtocIwxX/wT7TtUhdNhTuNJwFU6eycDnO74UO99591RklAaRV16HVt8JzH9qAgz9f4inzcuQuGU1Lu1nwC/DXkQWxwAzz3h8OFPWhVxnC+rteVj+zhJhSUyxLUVBJeB1N6D2zFHcd9OVMFxyO/Yd98FX4cGiV2Nlx/+6e6fglCuIfHcLSl1BGVPUQFDZUlQWHaZwdWohLMzUQQe0zOXES8+NEqd8dvQfkONoRVnxCdzB+wy8A0tW7YHbY8fObZtkTNx+TziO2oPIL6tDgysLC5+dBMPA7+Pp2JWijZF1+ACuuvgODBr8A6TlnkCe04GfDf2NgBvZx4vw+gcfyJwzDLoKhktvwYPjH0X9yWN44GqCiZfA0H8ILuk/EBcxPGXAnfj9injs3vQXAeluvTsCR0qBAl8jHPZCWGc9KeDGNNuHOFINEZI9D26QuVEjINrXwI0+5kZAW6/+vwE3fK4y5Kdswg8vJxD6Pby+KhUnXT0oKm+Do6IMxe4iFPuccDtduP+qGzHUMARrE87ieGUQVUVZmDzs5zBcdAveWbULjSXHYJweAsPFt+FJ2xrRE6G4MnVobrqJ4On9WJ/ggNdVhfdeWwzDRf1EO4iaM4MuG4I1+w8Is+wnN9yBKyXTENe5ARgsIXgDsGRlCnIqgNMlbSiroPZPQDLUfBe2xoXf0X8zhB0j4MZ59gx/X/rAjW/8LdV+i7/xs/+Qg3TaS0rVM4r+rPL3XmkSfqa//r3z/pWOfw3Q4Xhg0Vm1+iud5x447CXK0fvadzR7fMOLoaKhCcuXWdBe+pICNzSmBcGNTudz6HbORnfxC0r80/GcgBvdjlnoKX4GnfnPoqNwnuh1fPBWBBY881O0298CnGbA8SJ6S8jumCUskG77Cxq4QTbI+dIj7I7ZQMFCbF76hDwAyW4fd52jk7Hf1SMP2YeyWvHk3I0Yb9yDUbZ9mL3qhDjwbjI3bOvw/o4iUJaFDwTzrW9hwR9WooRMhW7gpd9vwGMxX4lAIJ1WmmxvRhOeMq3tC8OIeuUozK8cQkMQElf+3JKd+Pxoj1DTi6sApw94Zv6fkeVpF0HEN1afxcLfJ0PEAruBFeuSMC/yT3gh8n3MilyKmaaNmGz8AmNivhRQhTvcby75BDMWfIKZ0Z/AG+gRp2D+awcQ9eYRVLcrh++Pq9Iw3bQRz76xAy5qdXQBH65JwiOW9cgNAO7aHkTaluB565vYl1kim5AZOS68EZcl7efD5QvzY2B6dzkcfrW78vLrn2BS9OfCXGHoxMtL1mG6+Qs8at0AlxZDHxl7AM+bU4S5wjh9Oq1HcyrxhGmNAB4EN15/7TPMeGc7jpOB0gMsXxmHp8zv4QnzHzE96j08bV6DxxbuwFTLEYxdcEhEPwXciNqHKZYNWLsjR5zQDmqDNHej3c/sBtrub6AVTS2NElrQ6g/gqWefE3CDVHNVgvg0Lq2PuSFpR6lfYduHvaUKxNkWtx/TTJvFGQ+zbUYGlWG7gMTtZ4S5MuO1ZJRpOhLL1sZhduRbeN74juysTJ+7DjNs8RgbuwUZZBdQY+SVdZgRuQ4zFq1FSXubgDezlyRj5eZyETD1+powy/geFr66CpXNPWimWOuSFEyNOiwpTJluU4XQMCTlsBTZpdayfRD4IJODGWUuBDcoKNpMh629G12BTnT4g8LICLR3wWy1CFvj6aeeQ6CtE4FgO5ramtEa9KO5vQ3NIryaJtlLmFqV6XuZDnbYS3vxaU4ApOlnp9sxzbgXIQv24fOsBhnjlY0MFdmEmW8l46wmSLt0XTIeN23CvDcSUEv2UQ/w7toTmGHZgrhjteIs53uBGQtXIcz2uWjakMGw+NVNAgaQDRFu3CChI1NMe/G4KV7AwrJzTIT5Me9jduQbOJh2UoCmpMwuRL6ZiMoOxeb405pUPL7wEzz75k7YOzRmzeosPLIgCWOjGBpyDGOj0xBh3oxlW7NB9pS/NQgBNjp60dQalAdqsltmz5mHp2c9LzakTcluUcBaBzjWyHQJj4xX6Z8ZmmJLRdiiPUguOQ/CLNuahynWzZi6aBve31GBo05IiAyBkLfiKkXc4XSmF5ONO+X7j72VglIyozh/1x3AE6bNmP16Auo01tSbK/IE7KG+C4ExcgoyzzjwqGW1hI9xV/Tl1zbimbcTkN8LlDdznVuBuMwS6S9ffTfy3J0SNnSQa34X8MnHiZjz9jYRBQ60AyvXpGBS1JeY9dZ+VDMUqRt4bUM+zMuOCLhEzZx3Vh2Xerz60REcKgUmmBIRZt6NPyco5kZKVg9mRu5GWFQ6QoyJONuimF3GV7fimciN2JBQJIweqvhPm/cpHlmwR4kVW3MgGiYSjkWgUwEbY0zZGqCnUiT/b8Z/W6BLgI2m1k60BrvQEAiiuasHG7bvwfr4g2jR0gGr3z1SOfUfywvADf1h4Rt+HP/dD7HpOrjBB1Y+qH6bV/WQq+jdeT4/CG7QuWL4JkNV+PAv2VJG3QvD4FvxaOx6FJQDpaWVaHLnYteWDTBcdBu+9/OJyC3Ox9tvvyzAxqgxk+EtK0da6jHcct2vcMmgO5GRW4q3ln+EOZFWFBQWw+PNw4Qnpwh48YztA9TlZ+KX1w3E3T/9HU7mN4Lx8HPmRAkLYFbsMix943Vx+kNCJ4gDdCz1IG65+YcwXPMQ9p1uh+/sSd