Поиск и подстановка по нескольким условиям

74929 01.05.2015 Скачать пример

Постановка задачи

Если вы продвинутый пользователь Microsoft Excel, то должны быть знакомы с функцией поиска и подстановки ВПР или VLOOKUP (если еще нет, то сначала почитайте эту статью, чтобы им стать). Для тех, кто понимает, рекламировать ее не нужно :) - без нее не обходится ни один сложный расчет в Excel. Есть, однако, одна проблема: эта функция умеет искать данные только по совпадению одного параметра. А если у нас их несколько?

Предположим, что у нас есть база данных по ценам товаров за разные месяцы:

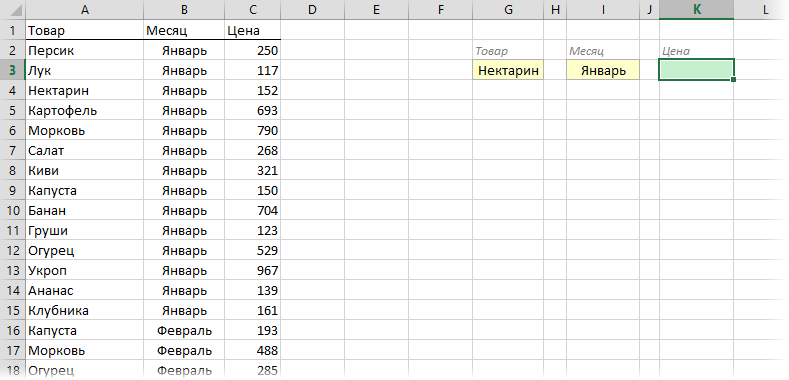
Нужно найти и вытащить цену заданного товара (Нектарин) в определенном месяце (Январь), т.е. получить на выходе152, но автоматически, т.е. с помощью формулы. ВПР в чистом виде тут не поможет, но есть несколько других способов решить эту задачу.

Способ 1. Дополнительный столбец с ключом поиска

Это самый очевидный и простой (хотя и не самый удобный) способ. Поскольку штатная функция ВПР (VLOOKUP) умеет искать только по одному столбцу, а не по нескольким, то нам нужно из нескольких сделать один!

Добавим рядом с нашей таблицей еще один столбец, где склеим название товара и месяц в единое целое с помощью оператора сцепки (&), чтобы получить уникальный столбец-ключ для поиска:

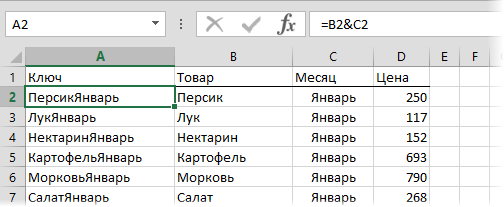
Теперь можно использовать знакомую функцию ВПР (VLOOKUP) для поиска склеенной пары НектаринЯнварь из ячеек H3 и J3 в созданном ключевом столбце:

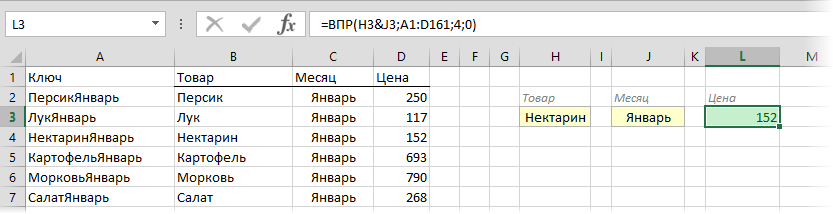
Плюсы: Простой способ, знакомая функция, работает с любыми данными.

Минусы: Надо делать дополнительный столбец и потом, возможно, еще и прятать его от пользователя. При изменении числа строк в таблице - допротягивать формулу сцепки на новые строки (хотя это можно упростить применением умной таблицы).

Способ 2. Функция СУММЕСЛИМН

Если нужно найти именно число (в нашем случае цена как раз число), то вместо ВПР можно использовать функцию СУММЕСЛИМН (SUMIFS), появившуюся начиная с Excel 2007. По идее, эта функция выбирает и суммирует числовые значения по нескольким (до 127!) условиям. Но если в нашем списке нет повторяющихся товаров внутри одного месяца, то она просто выведет значение цены для заданного товара и месяца:

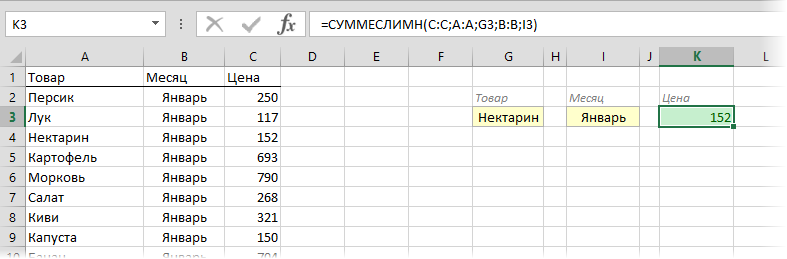
Плюсы: Не нужен дополнительный столбец, решение легко масштабируется на большее количество условий (до 127), быстро считает.

Минусы: Работает только с числовыми данными на выходе, не применима для поиска текста, не работает в старых версиях Excel (2003 и ранее).

Способ 3. Формула массива

О том, как спользовать связку функций ИНДЕКС (INDEX) и ПОИСКПОЗ (MATCH) в качестве более мощной альтернативы ВПР я уже подробно описывал (с видео). В нашем же случае, можно применить их для поиска по нескольким столбцам в виде формулы массива. Для этого:

Выделите пустую зеленую ячейку, где должен быть результат.
Введите в строке формул в нее следующую формулу:
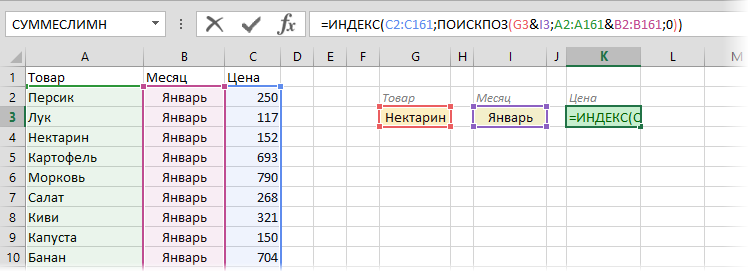
Нажмите в конце не Enter, а сочетание Ctrl+Shift+Enter, чтобы ввести формулу не как обычную, а как формулу массива.

Как это на самом деле работает:

Функция ИНДЕКС выдает из диапазона цен C2:C161 содержимое N-ой ячейки по порядку. При этом порядковый номер нужной ячейки нам находит функция ПОИСКПОЗ. Она ищет связку названия товара и месяца (НектаринЯнварь) по очереди во всех ячейках склеенного из двух столбцов диапазона A2:A161&B2:B161 и выдает порядковый номер ячейки, где нашла точное совпадение. По сути, это первый способ, но ключевой столбец создается виртуально прямо внутри формулы, а не в ячейках листа.

Плюсы: Не нужен отдельный столбец, работает и с числами и с текстом.

Минусы: Ощутимо тормозит на больших таблицах (как и все формулы массива, впрочем), особенно если указывать диапазоны "с запасом" или сразу целые столбцы (т.е. вместо A2:A161 вводить A:A и т.д.) Многим непривычны формулы массива в принципе (тогда вам сюда).

Ссылки по теме

MCH

21.07.2015 00:27:28

А как же СУММПРОИЗВ:

=СУММПРОИЗВ((B2:B161=H3)*(C2:C161=J3)*L3)

Либо формула массива:

=МИН(ЕСЛИ((B2:B161=H3)*(C2:C161=J3);L3))

Где вместо МИН можно использовать МАКС или СУММ (если сочетания Товар/Месяц уникальны)

Ссылка

Влад Куликов

23.07.2015 13:32:15

Еще есть вариант), на тот случай, если массив ниже или выше, или просто в рамках какого-то диапазона.
Данную формулу мне подсказал человек с форума под ником Евгений

=ИНДЕКС($A$1:$D$173;МАКС(ЕСЛИ($A$1:$D$173=G3&I3;СТРОКА($A$1:$D$173)));МАКС(ЕСЛИ($A$1:$D$173=K2;СТОЛБЕЦ($A$1:$D$173))))

Пример по ссылке ниже:
Скачать

Родитель Ссылка

Николай Павлов

22.08.2015 11:35:56

Совершенно согласен, Михаил. Но нужно помнить, что эти формулы работают только для чисел и при наличии дубликатов сочетаний Товар-Месяц будет их суммировать, а не выдавать первое встретившееся значение, т.е. это скорее для суммирования по двум условиям, чем для выборки.

Родитель Ссылка

MCH

23.08.2015 09:29:36

Пример с СУММПРОИЗВ() работает аналогично, как и приведенный "Способ 2" с СУММЕСЛИМН() с теми же самыми ограничениями (работает с числами и необходимы уникальные сочетания товар/месяц иначе получим сумму),но есть и преимущество - работает в 2003 Excel.
Я привел эти примеры, как дополнительные варианты "выборки".

Ну и еще вариант через ПРОСМОТР:

=ПРОСМОТР(2;1/(A2:A161=G3)/(B2:B161=I3);C2:C161)

Из преимуществ - не требует массивного ввода, работает в любой версии Excel, не нужно делать конкатенацию как в примере с ВПР, работает существенно быстрее, чем конструкция с ИНДЕКС(ПОИСКПОЗ) при использовании нулевого интервального просмотра (точного поиска). Особенность - при нескольких сочетаниях товар/месяц, попадающих под выборку - возвратит значение последнего совпадения.

Аналог данной формулы через ИНДЕКС(ПОИСКПОЗ):

=ИНДЕКС(C2:C161;ПОИСКПОЗ(2;1/(A2:A161=G3)/(B2:B161=I3)))

Требует массивного ввода и вернет последнее совпадение.

Для первого совпадения:

=ИНДЕКС(C2:C161;ПОИСКПОЗ(1;(A2:A161=G3)*(B2:B161=I3);0))

Но на большом количестве данных эта формула будет работать существенно медленнее , чем предыдущие два варианта.

Родитель Ссылка

Елена Рыжая

07.02.2017 17:12:53

=МИН(ЕСЛИ((B2:B161=H3)*(C2:C161=J3);L3))

Откуда появляется переменная "L3" в формуле, если ее надо вычислить??

Родитель Ссылка

ILYA_

24.07.2015 13:09:52

Привет Николай!

Я часто использую 1-й способ. Приходится анализировать информацию в разные дни и за разные, не равномерные промежутки времени. Чтобы иметь объективную информацию, дату и время я преобразую в вот такую штуку 25.03.2015 2:39:48 = 25_3_2015_2_39_48, далее ВПР вытягиваю значения, в пустых ячейках ставлю формулу =НД() и строю график .

Ссылка

Алексей Ст.

25.07.2015 22:02:52

Приветствую Николай! А нет ли в планах у вас создания видеоурока на тему анализа "что если" ?

Ссылка

vikttur

01.09.2015 16:34:39

еще один вариант:
=СРЗНАЧЕСЛИМН(C:C;A:A;G3;B:B;I3)
соответственно при дубляже строк он выдаст их среднюю.

Николай
такой вопрос, как вы выбираете функцию без мышки и её завершение?

в ролике в набрали "=ин" и что то нажали (время 8:55), и сразу появилось "=Индекс("

Ссылка

Василий Алибабаевичъ

23.10.2015 11:11:55

Ролик не видел... но нажат был TAB

Родитель Ссылка

Zoynels

18.09.2015 16:52:30

Использую чаще всео слияние всех трёх вариантов, только в качестве ключа использую IndexID=строка(). Затем суммирую по условию колонку IndexID, и уже через ИНДЕКС нахожу нужную колонку. Формула получается:

=ИНДЕКС(Прайс[Цена];СУММЕСЛИМН(Прайс[IndexID];Прайс[Товар];H3;Прайс[Месяц];J3);1)).

А для второго варианта можно исключить повторы используя формулу:

=ЕСЛИОШИБКА(СУММЕСЛИМН(C:C;A:A;G3;B:B;I3)/СЧЁТЕСЛИМН(A:A;G3;B:B;I3);"Ничего не найдено!")

которая вначале просуммирует все найденные значения, а затем разделит на их количество. только нужно учитывать что на ноль делить нельзя/

Ссылка

talot

25.11.2015 12:01:55

А для второго варианта можно исключить повторы используя формулу:

=ЕСЛИОШИБКА(СУММЕСЛИМН(C:C;A:A;G3;B:B;I3)/СЧЁТЕСЛИМН(A:A;G3;B:B;I3);"Ничего не найдено!";)

А почему бы для этого не использовать функцию СРЗНАЧЕСЛИМН()?
СРЗНАЧЕСЛИМН(C:C;A:A;G3;B:B;I3) и все.

Родитель Ссылка

IgorF

02.12.2015 17:54:05

Николай, для 3-го случая можно сделать формулу, очень похожую на Вашу, но без использования массива:

=ИНДЕКС(C:C;ПОИСКПОЗ(G3&I3;ИНДЕКС(A:A&B:B;0);0))
=INDEX(C:C;MATCH(G3&I3;INDEX(A:A&B:B;0);0))

Если в функции индекс в качестве второго параметра ввести 0, то он отрабатывает как массив

Ссылка

Николай Павлов

06.12.2015 14:32:57

Спасибо, что поделились, Игорь - весьма ценное уточнение.

Родитель Ссылка

Natalia

22.09.2016 11:13:45

Игорь, скажите, пожалуйста, если в связке столбцов А и В формула не находит связку G3&I3, как сделать так чтобы результат в ячейке был "0"...
Пробую вашу формулу, и в этом случае в ячейке выпадает "#Н/Д"....
Заранее спасибо..

Родитель Ссылка

IgorF

22.09.2016 11:16:48

Наталья, воспользуйтесь функцией
=ЕСЛИОШИБКА(ИНДЕКС(C:C;ПОИСКПОЗ(G3&I3;ИНДЕКС(A:A&B:B;0);0));0)
=IFERROR(INDEX(C:C;MATCH(G3&I3;INDEX(A:A&B:B;0);0));0)

Родитель Ссылка

Natalia

22.09.2016 11:37:06

Урааааа!!!! Заработало....
Спасибо огромное!

Родитель Ссылка

Трофим Кожемякин

21.05.2018 19:05:28

Игорь и Николай, большое спасибо!
Формула массива почему-то не сработала. В формуле были ссылки на столбцы, но название умной таблицы не отражалась.
Формула без использование массива сработала.

Родитель Ссылка

Игорь Яковлев

08.12.2015 12:55:09

А как посчитать сумму к определённой дате.
Например есть в 1м столбце даты (всегда разные) а во втором суммы. Нужно посчитать какая сумма выходит на 25 число каждого месяца.
Пример:
Дата Оплатили Выставили счёт
30.12.13 15000 руб.
02.01.14 12000 руб.
15.01.14 16000 руб
31.01.14 45000 руб
05.02.14 50000 руб
08.02.14 65000 руб
12.02.14 1000 руб
25.02.14 12000 руб
28.02.14 20000 руб
03.03.14 12000 руб
21.03.14 17000 руб
24.05.14 40000 руб
24.05.14 20000 руб

Нужно знать долг на 25 число каждого месяца.
Помогите пожалуйста.

Ссылка

Ульяна Максимова

08.05.2016 00:57:14

Здравствуйте, помогите плиз: необходимо чтобы автоматически выбирался месяц планирования (январь или февраль и т.д.) если есть значение в этом месяце? Спасибо

Ссылка

Natalia

22.09.2016 00:08:18

Николай, добрый день!
Пыталась применить способ №3, для меня он наиболее подходит, но формулу применить не смогла, выдает ошибку (#ЗНАЧ!)...
Создала аналог вашего примера, но формула продолжает выдавать ошибку...
Не понимаю в чем проблема:|

Ссылка

Aнна

11.01.2017 14:42:21

Наталья, Вы точно проставили фигурные скобки массива после написания формулы? (Ctrl+shift+Enter). Еще проверьте форматы столбцов -условий.
У меня все работает.
Большое спасибо за формулу)

Родитель Ссылка

Кирилл Гибизов

23.01.2017 18:11:04

Спасибо, Николай. Спасибо Игорь. Все заработало отлично.
Жить стало легче, жить стало веселее! =)

Ссылка

Дмитрий Болтянский

26.02.2017 20:39:30

+1. Просто спасибо. А то я был "уверен, что ВПР (VLOOKUP) - самая сложная функция в Excel, а я ее уже освоил - значит ничему новому меня не научить."

Ссылка

Дмитрий

14.07.2022 16:42:35

{=ЕСЛИ($L$471="имя";ИНДЕКС('БиЧ и ПБ'!A$2:A$2136;МИН(ЕСЛИ(ПРОМЕЖУТОЧНЫЕ.ИТОГИ(3;СМЕЩ('БиЧ и ПБ'!A$2;СТРОКА('БиЧ и ПБ'!A$2:A$2136)-СТРОКА('БиЧ и ПБ'!A$2);0));СТРОКА('БиЧ и ПБ'!A$2:A$2136)-СТРОКА('БиЧ и ПБ'!A$2)+P783)));ИНДЕКС('БиЧ и ПБ'!A$2:A$2136;МИН(ЕСЛИ(ПРОМЕЖУТОЧНЫЕ.ИТОГИ(3;СМЕЩ('БиЧ и ПБ'!A$2;СТРОКА('БиЧ и ПБ'!A$2:A$2136)-СТРОКА('БиЧ и ПБ'!A$2);0));СТРОКА('БиЧ и ПБ'!A$2:A$2136)-СТРОКА('БиЧ и ПБ'!A$2)+Q783))))}

Ну так, для примера, формула для поиска отфильтрованного значения с определенным порядковым номером ))

Родитель Ссылка

вольк

03.04.2017 19:45:31

а если столбы находяться не рядом , получмиться их склеить ?

1

критерий1	знач	знач	знач	критерий 2	знач	то что ищем
авто	1	ер	ер	11	аа	текст
авто	1	ере	ере	11	ап	текст
мото	2	ер	ер	22	ап	текст
мото	2	ре	еер	22	аптап	текст

Ссылка

вольк

03.04.2017 19:59:33

подскажите еще как сделать так, чтобы ВПР проматривала в отфильтрованной таблице только видимые ячейки и подставляла в другую отфильтрованную таблицу ?

Ссылка

Pavel Minaev

07.06.2017 13:40:38

Подскажите, пожалуйста. !!!
Никак не могу победить подсчет формулы с ИНДЕКС и ПОИСПОЗ... по первому параметру.
Задача такая..
Есть ряд параметров - по ним в массиве данных нужно найти соответствие по 2-м или нескольким совпадениям.
Причем первый параметр повторяющийся расположен в колонке, второй меняется и расположен в строке.
ПОИСКПОЗ - находит первое совпадение по первому параметру, а второе совпадение игнорирует...

Ссылка

Али

22.06.2017 02:18:46

Добрый день. У меня несколько иная задача. Имеется страница "Реализация" в которую при заполнении товара и даты продажи должна подставляться рекомендуемая цена со страницы "Цены". При этом на странице "Цены" один и тот-же товар может встречаться несколько раз (в том случае если он оприходовался более одного раза и цена закупки была разной). Так-же на странице "Цены" у каждого товара указывается дата установки цен, которая совпадает с датой оприходования. Мне нужно что-бы подставлялась последняя цена. Вариант при котором в разделе "Цены" цена закупки будет динамически меняться при поступлении новой партии товара меня не устраивает, т.к. при этом данные по прибыли за ранее проданный товар будут постоянно меняться, что будет ошибкой. Алгоритм, как должна выглядеть подстановка цены мне в общем-то понятен, но как должна выглядеть формула я сообразить не могу. Алгоритм (как мне кажется) должен быть следующий: Берём дату реализации и ищем ближайшую (раннюю) к ней дату установки цены со страницы "Цены" для выбранного товара, и вытаскиваем цену.
Я конечно понимаю что для этой цели нужен 1С, но товарищ (который попросил меня написать данную таблицу) не может забивать свои товары в общую базу.
Помогите пожалуйста. Данные по ценам нужно брать из столбцов I, J, K (страница "Цены";) и подставлять в столбцы J, K, L (страница "Реализация).
Пример по ссылке: Пример

Ссылка

Маракуйя

23.08.2017 16:01:55

Вам не подойдет такой вариант: фильтровать список цен по дате реализации, начиная с самого позднего (по убыванию)?
ВПР будет отбирать самое первое значение, т.е. верхнее.
Т.о. если у вас будет фильтр по дате, то и находить функция будет самую "свежую" цену.
Далее принцип поиска цены тот же, что и в статье...

Родитель Ссылка

Маракуйя

23.08.2017 14:11:18

Всем привет!
Подскажите, пожалуйста, как можно показать в одной строке в каких месяцах продавался, например, картофель?
Какую формулу следует использовать? Возможно ли это вообще осуществить стандартными формулами без допмакросов?

В моем случае требуется по одному артикулу обуви отобразить В ОДНОЙ СТРОЧКЕ все размеры, какие есть в наличии (столбец артикул обуви, столбец размер обуви).

Ссылка

Владимир Бутырирн

01.06.2018 11:53:00

Формула с массивом помогла, первые два варианта более сложные задачи, чем в примерах, не решают. Спасибо!

Ссылка

Ирина Ирина

24.08.2018 14:26:12

Добрый день! Помогите, пжл, я видимо на каком то этапе не верно делаю.
Есть список привязки номер телефона - должность, также есть таблица привязка должность -тариф , так мне нужно увязать телефон-должность-тариф. индекс _поискпоз делаю не верное знач. Помогите, пжл,.. спасибо

Ссылка

sp a

27.11.2018 16:08:39

Добрый день! подскажите, возможно ли использование формулы на 3м примере при поиске в разных книгах?

Ссылка

Александр З

26.09.2019 09:04:55

помогите как это в экселе прописать
В1=С1
В2=С2
если В3< В1 то В3=0
если В3<B2 и В3≥В1 то В3=С1
если В3 ≥В2 то В3=С2

Ссылка

Дарья Гайдукова

28.05.2020 14:22:10

Добрый день! Помогите, пожалуйста, если мне нужно сделать поиск не по отдельному слову, а по словосочетанию (одна ячейка), первое слово которого в одном столбце (выбрать из текста), а второе во втором. Всю голову сломала, ничего не выходит

Ссылка

Anna Matushkina

01.10.2020 13:07:59

А если условия - это даты и надо вынести название, если оно попало внутрь условия дипазона между 2 датами?

Ссылка

Иван Абрамов

28.05.2022 06:48:39

Приветствую!
Не смог на форуме найти тему...
Помогите решить задачу:
на приложенной картинке пример...
нужно провести выборку из умной таблицы по нескольким критериям...
1- номер гаража
2-максимальная дата(или крайняя(последняя календарная дата)
Вывод: состояние баланса на эту дату...
Или поделитесь ссылкой на форум...
Спасибо за Вашу работу!
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABfQAAAFECAYAAABhxb99AAAgAElEQVR4nOzdf3QUdZ7v/xfc7OrIKOMPYE2CJBIchiD7FSI4Ri4S5EyYURl+fFlY2vlyjcgB792gXHHxgCHCwoiLQ/Z+xS8XmcNX2sX1CAyGHbILBFmMIxDwu0iyKD8SfiQuouOggyMzmP7+UdWdquof6ep00qnO83FOjlJdXf3pd1XXj3d9Pu/q0dxcE1j/cKHKVK6at2crV/GrrKzU448/7uIdqKurU35+fqqb4SnEzD1i1rWwPlKH2LtHzBJH7BJH7DoX8XaPmHkH68o9YuZNrDf3iJl7xMw9YuYeMXMvo2F9qcpqffI3u0vmAwAAAAAAAACAztNzd2WtCsrnqijVLQEAAAAAAAAAAFH1PFEr6cQrejgzU5mhv4e1viHVTQMAAAAAAAAAAEE9Jan2+CBVNDerublZzc01Ki+oVVnhQlWnunUAAAAAAAAAAECSmdAveOgBS/38XM2e75PkVxUZfQAAAAAAAAAAuoSeEafmDlJBJzcEAAAAAAAAAABE13NQgVRbuVu2kvkNJ1SrAg3KjfY2AAAAAAAAAADQmXrOnu+Tasv0Sqi8TrUW+vySb75mk9AHAAAAAAAAAKBLyFDRKtWUH1ehL1P+4FSfX82rilLZLgAAAAAAAAAAYJEhSbmz31bz7FQ3BQAAAAAAAAAARBP5obgAAAAAAAAAAKBLIaEPAAAAAAAAAIAHkNAHAAAAAAAAAMADSOgDAAAAAAAAAOABPXbs2BFoaWlRIBBQS0tLxL9orwUCARUWFqb6OwAAAAAAAAAAkPYyhg8fnvCbKysrlZ+fn8TmpL+6ujpi5hIxc4+YdS2sj9Qh9u4Rs8QRu8QRu85FvN0jZt7BunKPmHkT6809YuYeMXOPmLlHzNyj5A4AAAAAAAAAAB5AQh8AAAAAAAAAAA8goQ8AAAAAAAAAgAeQ0AcAAAAAAAAAwANI6AMAAAAAAAAA4AEk9AEAAAAAAAAA8ICMhzMzVRvlRZ+/WauKOrU9AAAAAAAAAAAggoy3m5vDJjasf1iFZYNVTDIfAAAAAAAAAIAuIULJnWq9UlYr+YpFPh8AAAAAAAAAgK4hLKHfsH6N/CpQ+VzS+QAAAAAAAAAAdBUZ9n82aHdlreTza3ZuahoEAAAAAAAAAADC2XvoV78io9oOvfMBAAAAAAAAAOhKLAn9Bq1f45cKykW1HQAAAAAAAAAAupbWkjvB3vn+2aLaDgAAAAAAAAAAXUuoh351lV+ST1TbAQAAAAAAAACg6zES+g3rZVTbmSvy+QAAAAAAAAAAdD0ZklT9Splq5ZN/NsV2AAAAAAAAAADoijIkqWhVs5pXpbopAAAAAAAAAAAgmp5tzwIAAAAAAAAAAFKNhD4AAAAAAAAAAB5AQh8AAAAAAAAAAA8goQ8AAAAAAAAAgAf02LFjR6ClpUWBQEAtLS0R/6K9FggE9Ov/zEv1d/CUXz1XpJ8+X53qZiDNbS8bp4nle1LdDJhYH6lD7N0jZokjdokjdp2LeLtHzLyDdYXugtyCe8TMPWKWmL+b0i/VTUCayxg+fHjCb66srExiU4DIOIAAAAAAAADAC/Lz81PdBE+pq6sjZi5RcgcAAAAAAAAAAA8goQ8AAAAAAAAAgAeQ0AcAAAAAAAAAwANI6AMAAAAAAAAA4AEk9AEAAAAAAAAA8ICMVDfAS/4q/+tUN8FziJl7yYjZ9iS0AwbWR+oQe/eIWeKIXeKIXeci3u4RM+9gXbmXjJj9U911SWgJ3OA62T1i5h4xc499KrwiQ5KqF2bK57dMLShXzduzlZuiRnVl06c8mPB739iyI4kt8Q5i5h4x61pYH6lD7N0jZokjdokjdp2LeLtHzLyDdeUeMfMm1pt7xMw9YuYeMYMXZBjJfJ/8zatUJEmq1sJMnwofFkn9SAKBVLfAe4iZe8Ssa2F9pA6xd4+YJY7YJY7YdS7i7R4x8w7WlXvEzJtYb+4RM/eImXvEDB6Qceq4JF+xmcyXpCLNLS+Qv+yEGiQS+g78rt0jZu4Rs66F9ZE6xN49Ypa4dI1doN/tWjsnR1mSpMvasu6ANl1I8md4OHaBoUO1fXJfHdharZXHUt2a+Hg53qlCzLyDdeVeOsTMi/vi9kqH9WYV+O0W7a9Yqy8kSfkaWvoPGnhTkj8jzWLWGdIhZp1xLmv7vDSIGdJfxsDBko6fUoOKzOR9g3ZX1kq++ZYkf9sC6qdnn8vXKElN+w/oib2XFVAv/WzeKE35rE4/fbMDf22dKBDhl71y1Yutr7cE1NLyrb5taVHLt9/q22+/1dVvr+rnf/d3sZd74iW97f9n5fj26C8HJb3ZKRUpZgkvy9yRy9zGJCln7CitGS3bTj14Qujc2Tvntf77NVkPElYdf8BwSlbM7Ac+q8vasvWi7pnseO2zRs3fIj1tibH15HrFxa4To86UzG04aMy0Ij052DHxePL3laHfQgcsuzN4e/+Rmt9FR8Ys0sV22Lb8WaPmrz2txgjvl7pu3KSO+a2nmhHvXqF/H9jaMbFNx9h1ZcTbPa8ey1uPSVK6n28Fdfi6shyn0kWnXDt0g22vsyX1nM2WTLfqmMS60+X3/0a7d9aF/p3j65jPTI99uTr1xlVSt7Ng3s8SH+e0iPsRy343PN6x9y+ddS5rxXkWvCCjaJVfvkyfCjMrVV4zXycKffLLJ//bbtL5dlmjczVm7zG945hu+yF6NrkUPu1vn35aK19YpW9bvlXLt/ZE/rfffqtVP/951Dt8zgNvo3+cGqW0SuynYl94/5C+0vFPdWBwX90zpJc2Xbgc93ubIiSeOluyYtbjwmk98fzp1ptrsifa7pH9+8qcbnX/ECOxef5i67SuEKPOlOxtOKBeuu0WSfpUv3j+mN6x3BBNJufJjxd5ef+RKh0ZM+v+ILRfuaX1JDx4Qr/muevMbTs+XSFuUvr1xgmon2aM7tUp8U232HV1xNs9Lx7LA/1u19ohF/XT54+FEiRTptyu/WmWjHZK5rqKeKwaOlRrx/bqEsedZOmMawckX0fsy2+c8Jr+6z1mP+b3/0a7dyb/M5wCOqiTO+tsn91hn+X1fXnwtzV5qMYcO6Z9SfycqJ+fonOGSOefoXibCX61kUvozHNZ2+dyngUPyJCKtKrZL2X6VFbokyT5/Ktc9c63avrssrJu6atpY3vpnb2t0wP9btfTo3vZevk+0u+C5+7yBxT5l/23zzyt8vJltkT+t99e1d+/+GLU9wST+Zrwmh6++Z9CPfTzPv8b7faPk3x7NGzQQR0tW9R6EtV/nh54bIquU+v04IGz9ebAT3RP+VPqa/67t3lzIHjXPHizICDHss2797cr+vuGDWrS6Vd/pmPnWr9HWzcfon3/jhJQP907WDqw9ZjeU5Ge/EE/5exNzomo8856U4xe7Np/QPP2ftd+QmA7cFkSreb0BvWT1NDpMYum9YB7UfsvSOoXx3s6IUaR5m+I2JO4l60X8HmzJ0Qw0X1ga7VWHAte6LV+lLPHRIetj8++1pkIkwMRv+NlzQg7ufxUv3j+ou6NFA/10ugf9NKBrXXS5OTfLOgs6bD/iLw+zRtrYRcNRsLhtQvut/PQCIMOilnY/mBorqbcIjXtPxb67B66oM37czRqdF/dO1R652KsJbb1eZ0Xt5yxo6RP9yY1dpF7OdoTSs59Zdj+UJL0qX6x7mtNm9NH7++/rCmjzfdYe0Y5Pit00TO0j0bpsg70GapfPRfeoSJaHDddiL7MSKM2FDiYtNiFt8mMQbR9Xb/btTZKbIJtjbTvX3ks/DuOmlykX03u3F5ziUr279x6A7hpf53e/0F+KJHXYEvstR6LnNtEVoRkSDzzSIraY9rergOaV98v6u8q1rH+dMCbx/LGC6f1xJvmtAuXdV6K0HM6/SR1XfXrp3ucx6pjxzRPvfSzeUUp386dxwLn9hztuGXdf23esqPTzpeiHm+U2DEl0jIj7YujXl/EcV7UlXX+eW7k6/+BN7VWDAgK5RjiyTuceFeNylfOxRe0vczspV+wUhMfGhn+mWY+I9EuR57fl+u7yr4l+ud1hK6SWzCY3//4ZaMjq+PVsOP+xTbOZWPuG6KfO7ela8UMiCyjYf3DKiyrlc/frOYiqWH9wyr0Zcrv86t5VQJp/f9o1JYf5GvK6Fzdv7ehdXqf65Sly3r/oswT0hxl95HkgQOtVUuMW3VLnlusv/3bZ/Xtt1f17bdX9dJLL8Wc/9OatfpC+Rp6R5b0eev06+7xKWfnIjUeP6hhN2cpr3yP/lLBg+xanTwxRcNuPqdLkm7sn68vjr2vy/dMkT7eZ/b0b9TvfytZTw0Dv92iw5YhcJKk3xrLCN1EiHD33vm+r99/QcfOmYn/z+0H/WicMVj14urQ/3979ar+9Kc/6cofr+iPV67oxRdXtbk8ScoaPUq/st3JtdytNRMYWy5K79R/qicn99HofqfVGNrWeiW07QX63a61k/uGDhLGwWaUFl2s1grrjOa2vqX+stRP2vx8tVYqeLDJ0Yyhp7Vy7wH91LzhZUw32tig30vqmJhFY42lkWy3vGgm7A5sjS+h2VkxijT/ijgTh8Gbi0G5Y4eGem291sd5UWVI/vqwn8iE6RfpO1Zr5fMXwkqeBPr10plI8Tt2WZvWVhsnoZPjiUzX5LX9h23ZoYRj5G125TFJ/XopW8Zvb3MfSw+VKO+JtZ0HE6sdtv9w7A9y+xi/o/MX7b1lGi5elhGnXtLFCHGRZIu58/UUxG3N6F7avKVjtrcmR5JBir6vfPZitN/57ZqmXpryg4ua/3y1ecMzX4uGXgjdID2/tVpPhJLU1v1uL41SnX76/AXzc4z3xYqjNREetswosUxW7Hrogqt9ndGeaLFpXa5z329NAk28mBv6rM19RmnN5CItUtdO6idzWw3+BlpvcudK/3FZGm0edy8Yx6ym/RfU0K+fsmV24DFveGpIHzMR10u39TP+2/Y8MX7fMdp1f/3XkiL/rmzfybG+kx0zQ2ccy63LM+P6HxfSvrd0MtdVrrntHXAcq3rosvb/x2VNSfF2brAn8bP7KHT8jMS5j/6r/M65doh1bEj8mNL2vnjFxRjXF+3oONAVdOY1n6So1/+B327Rfv8/hxL2Roe+n+nfb97jIu9Qp0at1MTykeb7F+nfB++Jms9ItBqBV/flqSz71enbmcmZZ7DuJ5ou/j5s/ojHffM8L9K5bNv7hsjnh/Gc36UqZoAbGaVltSoor1Ewd587+201D1yoTJ9PC4ub5T6n/3u99m+fasrkvpo29qLeD06++LWa1Nc4QenTmjDxmraG3ly58o3RS//q1cSH6ZgHWknSTU06WfazqDv73kPHSDv36T9/e490rE45E+bp0k7nwK0mnd66VuqfL52zJPU/P6MvlK+sm2W7odDm+1xyxuHp/7lAP39hlf70xz+GdoJXrlxRRUVF3DGLVfLl/iF9pc8ajR6kMra7YNmMhr3HtOUHozTF7PlhiG/olnFBYCahJTXUX1TTaHvSKvzzv6sZz40K6x3dOvy39ftsMufXLRc7JGbRhA1fM3vhZ40epe2SdLwu7qRGZ8Uo0vzx6aWfTcmRPrss3RJ/v5Ckr48YJzKSpAsuvqObeT3Ia/sPe5IpR0+PvaB5e2OsI+vN7j6W6Qms1/uH9JXqOiZmiewPrNoq05XyuOlTSR0Tu0hi7itjHJOCibyAbf7rlCUpy7ZdSurTS7kylrdl34XInxMtjn2iLzNakqnDY9fGuo0Ym1Bbw/f9tnVg+e4Next1YHS+Rg3pJx3rur1Okhnv4G/gvWNGknPT2mMKqJ+yR+dryph+eq3ePG+vb902z//HRTPhf0H6QS8d2N+o7NF9bMuNOU8cv9WI7ep3u6a1GZ3Ix3ovH8sD6qdn5+Qo67NGzU+jMjHRdNa+OPh7T+V2builKXOKNEWS9KnePKbYo2Id++jNW3Z0TsxiHRsSPKbk9ml7X5x7Mb7rCy/qzGs+SVGv/7/+eF9rR0NJ190xRjfurNOlz5ukm415YuUdvv68UVK+hhaODH//oNj5DLe8ui/f92a19qn1GnfNc306bSRJp29npohlcsz9gfMmqxT5uJ8zdpSincva9h+KvG+IfO7c9nE0VTED3OhZK2nwwFz71NxBKmjPUo81aMtnUtboHN1jTupx4bRe3H9ZoyYXafvkvrZhj14SaAnE/LvyzRXj78qVsNec+g7+iaQ6NX3cZJv+tXnHO2fwSH1auUiN+onuKd+jh30/aZ3JPBh/9457lNW/Tk01/6Smcz/RX9whSXX6veUAfWnfCzqmeRoxxj6gyTjw5ui7UR5WE+l9ve75B91TUKdjFePi6p0fLWbPPP20vvnmD/ry0iV9eelLrfnFmojzuRXod7umDZZ0S47WPFek7ebwzazRuRqj4IGhWj993vibvz+5F0WjJhfpycGf6hfmHff7p+VrlD7VL56v1sStn4bms7Zj4tZPlTV6lBYNNeaXOjdm0TTtP6CJz9fpwOB8/WpaHLV24pSMGEWaPyhr9Cj96rmiiD3ts//rUE1Ro178t9b13rj3gH5x3LiQivQeKfnrI5hIer8+8vbX1ndMdF4v8uz+49hFHZCU1ee7MddRrnlSedZxPGzPdt4RMYu0P2gwT8Sz+9hvjkXruR+XFMZN6hr73kQd2Nq6bf70+Wo9sfeyZbRE5PdEi2OsZQY5Y9nRsWvPvi7Svt/rOjrePXRB7x2XNLiPnh3St7XUlpmwO19/Qe9/1kv3jMnVPbd8qvfqpdC2Fsc8HXnsira+vXosN5I/5uvdpJZ5MtdVtGOV1JW288vasq7aOM6qr560nHfHOm4F99HJjllboh0b2nNMaa+2ju9dVWefd7R1/R9RHHmH627OkTMHERQ1n5Egr+7Lg4Kjg2KdnyVbVzq/De4nzsd5M66tc9mO0pViBkTT0yfJv2a9LMVxVP1KmWrlU3GChfR76LJe+7dPJfVSlqUudePeAx1yAO9MgYDx9/erV+vvV6/WihUrtWTJc3pqwVMKBKQrV67oypVv9McrV0LzBv+cegx6Sg/7fqIvdv4slBxv9I/T7p3S0NLwuvTGAdj6/zn67k1Z+ouh+fqi9p/1RcF96ntTf/V2fM4X56Shk6foOuv3UJP+81idVHBf1A4gEd/32y36qNaonxfvAdkZh+DfsueX66svv9Tata9EncetUI+7dc6km1HPuT2cB5NIB/8DW6s1f38vPfncKD3iCGyu5UJizLTw1606M2axGPWwL0uDc2K2N6gzY+ScP6hp/4HQTQCnrFukLVtO2/Z3wSRu0/4DUU+8krk+AmZt+9BFYxsifcdkzOsVnt1/DO1j1NV19PaxrqPQtnD8YswHYsW7nZ8xkxYdFbOw/UEw+W7e8DC+k/HgKn3WqM2JlCtJWdzMpHQnbW/x7CsjyfpBP+WotYTE+YuXzRGQMnqUO5nrKJjIsn5OzDjGWqbJGctO/a1GWLcRYxN8LcK+v6H+oprUS/cMcdyQGptj9NLd17V7nSQz3sHfQHA/N2baUI2RUXZM6qtRg1t7uLUm7IyERNbgvso6flHvmPXdFec8VtGOXZHadX8csYm0vpMds846lreOVjRqsnfGwxO7gqTuT0IdzSzHqn6362UzaZ7q7dwmQk/hiOe1EfbRnbIPjnFsSPSYEs++OJ5jZqzz/66sM4+dsa7/nQn5YI/9rDuy4ss7DLpPOZLRI9/xfitrPiNRXtyX54wdpZfHtv57gMukdnt15nYWsx1txDvicT/GuWw8+4ZY54cx29pFYgbEkhF8IG5hZpllsk/+5sQfjCvJOHn6r31D5TLCHw532TMPq7EK1tJ68smntHz5Mn399de6fPmyKir+QS2BgK5cuWI8ELfl25j184N6DHpKE8ufCj2ExvmA2b6F83Rj7Vq9X/bPUv983RhhGcED8I19siQZB1Hr8LgbJzxjPOgmdMfcfLCt5umBh0ZGbVv4+4J1/3+ie+7Jkk60+fUkxX7uwPpXfxlXnOITPEA02g4QwaFX7R0+3+PYMc036zkGh4se2FptbMMRhohOGdNPE/c1atrgHD35XJH02WUFx2K882ajnn2uSL8KvsksYxG42Kjpt3RmzCLUrt5if92IX44xHLmNK8nOilGk+eMRGhlkacv9Y8yHl+29LEVJ2iZrfdgfqpSjNc85HgM0OF+/mqaoMYnknSjzOksWaXC+fvVcvice9mjltf2H7fd0vM58KFOkdWR5+F6EhzNFW6+xNO49oFER6uhatTdm1v3BpjcvaMXzv9fP5o3Sk88V6cngTC4eOBWU6rj9ok+R/kKdt73F3FfG0KQ+rfsNc5/YQ6c1b+t12j7Z+I0bgudYF7Riax9tnxyMb/DhwbHj2ONC9GW+FqVtHR27ttZtpNgEMxaR9v09LpzWvHXS2jlmOSkZI8hGeeT8NJnxDv4GnjS3x6b9B/SEZDmXj3yzKXghbSQfvyspvBd0tHni+a1Gatc89Wuz5E6k9S1581gefHaJ1Neyn/XGNtoeydy+e+iyXlt7QLIdqz7VL54/bcyQ4u3cYCm5EyyrFKNTi3MfvXnLjk45fkU/NhyTpiR2TNkUx764x4UYx8zkDSJOic47z419/d9j0FN6YEKjdvvHhUYB5fj2aOBN9uIk0fIOPQaN1DDfT/S2/2favlOyPWw3jnyGG17clzfuPaA3pxXpV88F5+zc/XiHbGeDrb9ny7Rp0kQzZ2DPM1xW0y29zIeGRx5tFvl85LLeiXAuG+++IeL5YRw6Mx8DJKpHc3NzwltiZWWlfv2feclsT5f2V/lf68EJ423T5s2dq7WvvBLX+3fs3KUZUx4MDY3sDiLFzA1i5t6Onbv011Mf0sTyPUlsVfeVzPURPHHMjlBPMJSA/8x9MjRd8Vtwj5glrivHzvoA1644wjGVsUtGbJwPtevqOiveAesNNI+XeuFY7h2dvT9Jh+08GTH7p7rr2p6xg3ltX9xeXCe7l8yYdZd9eWdtZ10tZu05P0zWPvVXz7Wri3S3U1dXp/z8/LZnREhGqhvgNc4bcS+bQ20QHfFxj5h1LayP1CH27hGzxBG7xBG7ztUp8TZ7hzftv+DJJKcT26h3dOq6SpPtnO3bm1hv7hEz94iZe8QMXkBC36UAv2zXiJl7xKxrSdb66KELWvl85B4LwQeubkrKJ6UPfgvuEbPEddXY9bhwWk8Ey0N0UamKXTJi0+PYMf3UY71BOyPeXoxLLBzLvaMz9yfpsp131eOXG+myLtxIh/XW2diXu9cp5wxdLGbtPT/ktwkvIKHvEr9r94iZe8Ssa2F9pA6xd4+YJY7YJY7YdS7i7R4x8w7WlXvEzJtYb+4RM/eImXvEDF6QceTIEbW0tCgQCKilpSXiX7TXuqOd/7o71U3wHGLmHjHrWlgfqUPs3SNmiSN2iSN2nYt4u0fMvIN15R4x8ybWm3vEzD1i5h4xgxe0+6G4jz/+eDLbAwAAAAAAAADoBngornuU3AEAAAAAAACAJKirq0t1EzyHmLlDQh8AAAAAAAAAkoDe5u7QQ9+9dtfQP/XJlyn+Ct6Sl9lbJ5svpboZnkLM3MnL7C1JxKwLYRtOHWLvHjFLHLFLHLHrXMTbPWLmHawrd7h28K6Bt95APsYlYuYeMUvMwFtvSHUTkOYyhg8fnvCbKysrk9gUAAAAAAAAAAAQTc9UNwAAAAAAAAAAALSNhD4AAAAAAAAAAB5AQh8AAAAAAAAAAA8goQ8AAAAAAAAAgAeQ0AcAAAAAAAAAwAN6SlLD+j7KzLy19W/htaluV/JUlyovs7fyFu6K+PK+hb2N14N/D6/VmXjmcyzP+fq09afjbuKZ9eOVl1mqfbapp7Xx4ejtAQAAAAAAAAB0Lz0b1vdRYZlUXvOJmps/UXPzF/L5b0yDpL6ZEPdtjDrHvoW9VeKfpQ3Nl3Sy+ZJONr+l6bWLNM6WRDeWU3J8pfaE5rukk6vGR1+Of5aOlN3lKqkfpqFKv66Vhj9UrAGJLwXwpuCNuARukAEAAAAAAADpqucrZRkqKP9Cs3ODk77R3PKrkv87qk5ly9rpzPo5Wl47UotrPtDigkhznFbDcUm+BzUmNG28ZpePlGo/UqNtObO04e15kRPrDWv1sl8aXl7aupyiCm3wSUcqqxLuXX9m9zYd0Sw9Mfv2BJcAeNUuLfbVa3GNeYOsZqVUNkcbG1LdLgAAAAAAACC1eh6XNHjgVdvE3IFXJV2rKg9n9AfM3qWTzbs0KzfaHLcrd7Ck4ydsvfH3Vh60JPmNf9uS9U4NH+mIpDsG2hPvOYPsNwbccbbD+nlrNS3TXt5nsWM9GSV8rPOMtyVD9y2MVcrHHNlgKSm0b6HRQ9q+XGeJIIX1qnZ+Rni7oiwH3Vv1Dr3hW9j6282dpyd8B/Xr3fTSBwCkP/v50viYN7TtJR8t51SMdAMAAADSVs9aXdUgZ9I790+K2Kk9zYxZZZbYyRyvjQ27tDjzLqM3fqiczimdrJV0osKRRLdcXOV+X8MjLHvAwCGS6tWQQK/ifQvvMkYXzB1vf6G6VHmFi3SH31L6xz9Lb/gsF2oNa/V05SRLeaAPtLjgoJaXtq8W/5GyuzTuxELLMjeqxJKwP7N+vPJ8spQv+kCL5SxfJKnAXrpog8++HODMqfqwaTmDRqagJQAAdLZdWm85j9tTLi1/JfpzoEr0Vus5YXOF2REk0ki3CjpQAAAAAGmiZ6obkFrjtbz5LU3XQS0vnKo3JE33V4T1ij9y/Pt60ZkgLzR7QeUW68cF0htrHHX310Sv3R/ZRpWYNwyMev3O0QXmMn1vaXmRZXKwvE/wQi13nt6MVB5o8KD21eIvWKk9oRsdt2vW/FlS7TbtbZCkXVpfdtARO+c8MbS3bQAAAGlhvJZbzuMaTxzU8EEDI8y3S7v81k4oAAAAALqLbp3QN4Y0T5X8wV5QI/WGz15uRnI+mNZMVGlIr3kAACAASURBVGujdlWb/3472NM/2IP/Lp0cPEvSEOVGLfnj1PpQ3T0PbdO4sFI6xmiB6cXhF25jimfJNhrAVpbnLi0f/JbtIb6SJFt7w79zGGfSPff7Gq6DOtkgqeGEPpaM2FmXGemBxI7PLeFiFHFoPHEw1U0AAKBTWEvulOgtvRnpeUoNJ/RxQb1ejnguN17Laybp14Xm9MKP9ERzeIcVAAAAAN7Us0AZOuHsQd3wZ4pYiiedNKzV02UHNbz8g1CP9wGzd+mkf5bknxpWl94mrMzOeC23lJE52XxJswfVSwXfV04CTRswe5c2+By9/s2keXSWmwe58/SmdUTB8anhteqtpW9qVmq4f2rbSf02TPfbY2D8OUYaRCq5Qx19WAx4YJKG+1e1lrVqWKuX/SP14wd4QDQAIP0Zz4EyO3kMWhX9uUe1Q/RE6JzqLU23nL+e2b1NRzRLG2pWarg2qqSd53gAAAAAuo6egyUdP5Vhm9hwKkPSVQ1M64R+5IfZ2pP1A5VXIB2prLJfSDV8pCMaqbyo8TEfpmvr2e/OmOJZUu0irQ/eWMgdpDskvVEVfkG2r2pjjJsHwREFMer5587TE742GmR7eLDsMTDb9vEp9w9cCxtdAOTO05v+IVoe6lm4SHf4Yz3gGgCA9DRg9kJNj6d8ocZrfPBcrrpU4yonaU9zhcbkztObZueOmJ1VAAAAAHhGz2KfVFt2o9aHesN+V6VlGSoo/0pFMd/qcUUParqcte+lfa8s0hHN0vgiqbUOvCWxrl1a7Nso+RZGSTCe1saH79JyrdSLkYZIx92+Ui221eYfr9nlI8NHD1SXqsQvTZ9v1lutLnX0tA/W849R/qdhrV72K0qNVlPtIo0LLdcZA6NtR8rmtPaqDraljQfe7qtqo23onooqbCM9lqf1zggAAJPzPK56h96IdJ6UW6wfFwTLPyo0mi1yZxOjbCMAAACA9JBRtOoT+XWrfIW3qsycWFB+UW/PvprShrXXmfXjNa7MUne7dqry/JJRq75CY8wH4ipzqsZlLrK8M/i6qahCe8rrNc7XW28Ep/msNenNBL71QskXoWa9a7dr7EMjtbxsm/Y2zNOsXHMI9sBS5VnbopFaXHOp9eZCUYX2nDKfDRBUsFJ7mlsfsJYzaKTkX2T73sPLPzBrtEbpZe97yxj2HVyu7SG5Rtv2aLzGFfbWcuvnOh/QW2v/XGfbAAAAuq2iUi1ec5fyMoMTrOelxjnnyfmXtLzods2qWKlphb2VZ8453W+eD+ZWaENV7/DzPG6OAwAAAGmhR3NzcyDRN1dWVmrcQ9OT2Z60l5fZWyebL6W6Ga7sW2g8lK39NykS48WYpVJeZm9JImZdCNtw6hB794hZ4ohd4ohdPHZpceYOjU/CA26Jt3vEzDtYV+5w7eBdA2+9Qac++TLVzfAUYuYeMUvMwFtvSHUTPKWurk75+fmpboanZLQ9CwAAAIBUOrN+leTf1e5kPgAAAABvI6EPAAAAdHEDZu9qLWsIAAAAoNsioY82jVl1SSdT3QgAAAAAAAAA6OZ6proBAAAAAAAAAACgbT127NgRaGlpUSAQUEtLS8S/aK8FAgE9/vjjqf4OntKjR49UNwEAAAAAgJBAIJDqJgBA2qirq0t1E5DmMoYPH57wmysrK/Uvh5uS2Jzuoar2fKqb4BnFBdmSiJkbxKzrKS7IZn2kCLF3j5gljtgljth1LuLtHjHzDtaVe8UF2VzXe9CPRmSx3lwiZu4Rs8T8aER+qpvgKXV1dcrPJ2ZuUHIHAAAAAAAAAAAPIKEPAAAAAAAAAIAHkNAHAAAAAAAAAMADSOgDAAAAAAAAAOABJPQBAAAAAAAAAPAAEvoAAAAAAAAAAHhAa0K/+kZlZt6qzIXXprA5HaDmGRUXZKt4xd6ILx9akW28Hvx79FU1xTOfY3nO15/a3Bh3E5s2T1RxwTM6ZJvaqG2PRm8PAAAAAAAAAKB7yZAytP7hPiqrTXVTkq1R2x69T+uORp/j0IpsLdk6U8tqX9DdkqS9qih4RCWPSht++ZiyrMvRUm2oDU5rYzk1z6i49D49pXf10oycxJp/brf2H5WGLHgg4mcixWqeUXHp66F/DlnQjnWNME2bJ6pk9WHzXyM0Z9t2Teqf0iYBAAAAAAAAKdezYf2NKqu9qvKaiyovSHVzkqdpc6nWHR2hOdve1ZxhkeZo1PmTkiYXm8l8SRqrqQtGSEdPqNm2nJla9svIyXyde1Wbt0pDFsxtXU7hC1o2WarftTvh3vVN71aqXjM1gyRxF7RXFaXHNWfbeVXVnlfVtqXS6lJtO5fqdqWLvXpr10PaUGvEd8MCad2myCNsAAAAAAAAgO6kZ+7si2puvqjZualuSnJlzdiuqtpYvXpzlJ0n6eQpS9K9UQd3HbYk+Y1/25L1TmdPqF7SgNvsiffMXPuNAXec7bA496qeKrCX96mosc9ilPCxzjPRlmw+tCJWKR+z1I+lpNChFUYJIftynSWC1FreKEr5ovB2RVlOV1dTpZ2T57duW/0f04zJh7X/3fjLLCGWsSq13EBrbjisIblptoPyCsdvOqyUmPm6cx8U9zLaWn6k+SLtu+JpB7qPWNtDe7dZU/B4xjYXP/s5wERugsfgJlb2ko+Wc6p4969ew+8bAAAA6N4Pxb372U2acHSpSgomatu5vaoouM/ojf/sWHOOBp09KqnhFUcS3XJxddsgDYmw7KzbBks6rvMJXLAeWnGfMbrgkbH2F2qeUfGkpRpQYfYMrz2vqoqZ2llquSA596pWW3o3V9W+qznDDmtdWftq8devvk8lDfMty3xdSyyJtabNE1VcKi2zfq6WqsSZfBu21NK281o22b4cL2g6ezxsWmbuiBS0JH1ZkxlLtIlyRikReyTKoRXZKt5XrGWTE11GpNdeiXCDb68qNgwy9xvGfmW1JQETXzvQXcTaHtq/zZrM4+wctjkXGHkVv/hjdWiFcYwMnRNaS0jGtX/1Fn7fAAAAgKFbJ/SlsSqt3aQJOqx1kx7RTkkTKl4I6xVff3KQFjgT5JPMXlD9H9DoYdLODa/aevpv2/C63HldS4IJzJNLtSFsdIG5zMmbVFpomRws7xO8UOv/mF6KVB4ob2D7avEPW6oNoRsdOZpUMlM6WqmDZmLurdWHHbFzzhNDe9uGtGOMsDGTGblreDh0KrQxEuXuZ8+r6tmx0d8fxzLiYx2xkaOR4+03z+JqB7qNWNtDcrbZRm0rq9To8seUnbRWdweMvIpfvLHaq/e2WjuhpD9+3wAAAIAhI9UNSKXggzcnVJxXVaH579Js7Zy8yXZRMGS89cG0RqJ6Xenreq/mBd1dmKNJv9ykswWPqKRgaWiuCZNnSkel7Lgf5Nn6UN2mzRNVUrBUEyrOW5L3xmiBCSXhFyt3j5kpbTVGA9zdX0ZZnklLVR+cwfF9JElHl9raG3EeK2fS/bZBGqLXdfasJJ3SGUn1pdnaGfZGR8915+dqppbVev9itLnhsERuokNkzZivCavX6OC5x3gwbicyRqIU26a5HYkSexljVbrtlJ6alK11kqz7wOiMcmQDShixgY7R1nbftLlU+8dX6KX+8nxv585me9j55E2qYuRVVHHF6twpnRl2XGcKsrUkOC10LpfI/jX98fsGAABAuui+PfTPvarVqw9ryIJ3Q0nzrBnbVVUxU9r6SOy6mWFldsaq1FJGpqr2vKbmHpeGDVJmAk3LmrFdyyY7ev2fM5Lm0Q1uvXnQ/zG9ZB1RcPKR8Fr11tI325ZqyNZHbHXzEzGhwh4D488x0iBSyR2P1dHPuu8hDdm6pnWI9rlXtXnrCI2+j+REUtQ8Y98Wa6q007p9I20EH/69bNtSDdHrWtLGPqhpc6nW5TlGKaHbspbm6pT64Ode1erVg3lYfYIYeRW/uGN1dLBmhM6pNmmC5fzV7f612+P3DQAAAA/pvgn9KA+ztSfrc3XbMKl+1277hdTZE6rXCN12W7SFmw/TtfXsd+fuMTOlo0v1VvDGQv+BGiBp577wC7JD+16PcfPALH0Tq55//8c0o61aobaHB8seA7NtZ866T6jcPaaNtnVF/R/TSxWDtW6S+UyFSUs1oCLWA5jhSuFc8yaUGd9S0bOwi2huOJy8ZdQ8o5JdD2lD7Qu6u/9jesm8+RjtZmrT5onG/N2ovARisyY9O/I5G6Ft9uwJ1VvL422V/Rk2iFvWjPmaEE9JPriI1VjdGzyXc7l/7c74fQMAAMCLum9Cv7BYE+SsfS8d2rRU9Zqpewul1jrwlsS69qqi9HXJWoPTplHbHr1P67RUC9qTYCicqzm22vxjNXXBiPDRAzXPaMlWaUKJWW/V2bs5VM8/Rg/nc69q81bFrmd7dKlKQst1xsBoW73zwWI1z7TZA+/Qvjba1lUVvmAbiUCP4WTK0aRfWkd5kMxPhWSMRHG3DPMh5BEcWpFtPJQ70vNBgCSKuc069vvLJhsj03hodxwYeRW/eGPV/wGNHva63gueE5rbauTOJtH3r90Jv28AAACki4yG9X1UWGYppV97ozL9kvSN/M1fqChVLWsnW/1RSTr6iIq3Sq11RI0H4spR+z6szmjhC9qw4LhRWz84zVZv3kzgWy+U2qpHHxfj4Y/rVleGaodnzdiuqtueUbGtVv0Izdl2vvXmQuEL2nB2oooLHmld1LCl2lDbmgjLzB0hbbXXsh+y4F3zoiVKT6TJm4xh38Hl2h6Sa7RtgyaqJFSv1ZzHmYBz1tB3tA1AF9H/Mb1UcULFlt/0hIrWfc2hFUYPRknS1mzt1AjN2bZdk/rvVUXBI1LFeZUWxlhG/xe0bF92+H6oUJIsy7jNuOEoBffhknU/Hb0dHRQXdGmxtoforxnH8bMlbWyzSFzhXM3ZcJ+KC4ITqOkeVcxYWbfVHE0qX6qnJmWHqsLHt3/1Ln7fAAAAgKFHc3NzINE3V1ZWasCInySzPWmvuCBbVbXnU90MVw6tyNYSJeMmhXvFBdmS5LmYpRIx63q8+LtPF8Teve4Xs72qKKjSvUlIMHe/2CUPsYsH26p7xKw7Yl25R8y86UcjsvQvh3kijRvEzD1ilpgfjaDbqht1dXXKz89PdTM8JaPtWQAAANJT0+Y1UsV2eoujy2NbdY+YAQAAIB2R0AcAAN1W1oztKk11I4A4sK26R8wAAACQjkjoo013P3teValuBAAAAAAAAAB0cz1T3QAAAAAAAAAAANC2Hjt27Ai0tLQoEAiopaUl4l+01wKBgB5//PFUfwdP6dGjR6qbAAAAAABASCAQSHUTACBt1NXVpboJSHMZw4cPT/jNlZWVOvXJl0lsTvdwsvlSqpvgGXmZvSURM7fyMnsTsy6E9ZE6xN49YpY4Ypc4Yte5iLd7xMw7WFfu5WX25rregwbeegPrzSVi5h4xS0x+fn6qm+ApdXV1xMwlSu4AAAAAAAAAAOABJPQBAAAAAAAAAPAAEvoAAAAAAAAAAHgACX0AAAAAAAAAADyAhD4AAAAAAAAAAB5AQh8AAAAAAAAAAA/oKV2rhZm3KtPyt7A61c1KoupS5WX2Vt7CXRFf3rewt/F68O/htToTz3yO5Tlfn7b+dNxNPLN+vPIyS7XPNvW0Nj4cvT0AAAAAAAAAgO6l5/qHb5T8n6i52fjz+yS/Lx2S+mZC3Lcx6hz7FvZWiX+WNjRf0snmSzrZ/Jam1y7SOFsS3VhOyfGV2hOa75JOrhoffTn+WTpSdperpH6Yhir9ulYa/lCxBiS+FHQQ4yZM8AbOeG1sSHWL0lMwzos9vz8CAAAAAAAA2q/n7Lc/0aqi1glFc79SgaTjpzJS1qhkOLN+jpbXjtTimg+0uCDSHKfVcFyS70GNCU0br9nlI6Xaj9RoW84sbXh7XuTEesNaveyXhpeXti6nqEIbfNKRyqqEe9ef2b1NRzRLT8y+PcEloOPs0vrKSaEbPHvKpeWvRB4BgnZoWKunKydpsS/VDQEAAAAAAAC6hrStoT9g9i6dbN6lWbnR5rhduYMlHT9h642/t/KgJclv/NuWrHdq+EhHJN0x0J54zxlkvzHgjrMd1s9bq2mZ9vI+zt7L9t7j4T3I9y2MVcrHHNlgKSm0b6FRQsi+XGeJILWWN4pSvii8XVGW0+WN13LLDZ7GEwc1fNDAlLYo/ZzWxtJt+nHFPEX9CaPjOX7TYaOOzNdjjqCItQzbazFGuljni7Tviqcd6D7a2B5ijvxxHsecx6m2tkXExm81Lm5GAdpLPkbZVl2WgvQiYgYAAIDuJDyh3/BnqpU0eODVzm9NJxuzyiyxkzleGxt2aXHmXUZv/FA5nVM6WSvpRIUjiW65UMj9voZHWPaAgUMk1ashgVIs+xbeZYwumDve/kJ1qfIKF+kOv6X0j3+W3vBZLjrMXs2t5YE+0OKCg1pe2r7Ew5GyuzTuxELLMjeqxJLMOLN+vPJ8spQv+kCL5SxfJKnAXrpog8++HK+wXjiW6C29yUiKpDqzfo5+/dC6GDfk0PF2abGvXotrzN9rzUqpbE5o37dvYW/lVT2oDTFHUMRYRsNaTbPuM/xDtLww0g2+XVq85vvmfsPYrzxtSbLE1w50F21uD22N/CmqaD2+msfY1pvrsbdFxMZvNV7xjwLct9A4B2ndZitat9WwfW+FBztQxIuYAQAAoHtxJPSv1ULftVLBV5pbFPkN6WW8lje/pek6qOWFU/WGpOn+irBe8UeOf18vOhPkwcRTbrF+XCC9scZRd39N9Nr9kW1USTBBfHyl9oSNLjCX6XtLy63rJljeJ3jRkTtPb0YqDzR4UPtq8Res1J7QjY7bNWv+LKl2m/Y2SNIurS876Iidc54Y2tu2FDBGgJgXjoNW0VMzmRrW6umyIZSbSrXqHXrDt7B1P5Q7T0/4DurXu40E5phV9meJuF3Gmd3bdMQ6CqnoQU2PeBPUOiLmdo19aKTt1bjagW4j9vbgduSPcdydXhxcXuxtEbHxW41XvKMAd2mX39oJpTsjZgAAAOhebAn96oU3yq+rKq/4fbcoc2H0sp4q+YM9ekbqDZ+93IzkfDCtmajWRu2qNv/9drCnf7AH/106OXiWpCHKjTuQrQ/V3fPQNo0LG5JujBZoTSy0GlM8S7bRALayPHdp+eC3wi+ibe0N/85hnEn33O9ruA7qZIOkhhP6WDJiZ11mpAcSOz63JA0urAbMXqjp8dy4QHwaPtIR6w0uv+yjUNApzpyqD5uWM8hdAjPWMgYMHCL5d1h6Pw5UXoG5T4nKKEfmLHEGxMP1yJ/qCi3XSs2O2MGBbREdJ65RgA0n9HFBvV6OeC43XstrJunXheb0wo/0RHN4h5V0QswAAADQnYQS+tULb5XPf1XlNRc1uztk8xvW6umygxpe/kGox/uA2buM4fX+qbHru4aV2Rmv5dYh+s2XNHtQvVTwfeUk0LQBs3dpg8/R699MmkdnuXmQO09vWkcUHJ8aXqveWvqmZqWG+6e2ndRvw3S/PQbGn2OkQaSSO16ro19dao9V9Q694ermDWJylLzY4DO2LcoapZmiCvP3b7n5WDtSeTF+R2fWz9HywY5RSui2rAm8Nm/4uR75Y/bOnx9hxJvYFtGx4h4FWDtET4SOl29puuX89czubTqiWdpQs1LDtVEl7TzH6+qIGQAAALqTnlIwmS/5/N0kmS9FfZitPVk/UHkF0pHKKvtFQcNHOqJYiSfzYbq2nv3ujCmeJdUu0vrgjYXcQbpD0htV4RcX+6o2xrh5EBxREKOef+48PdFWTVvbw4Nlj4HZto9Pue9BHTa6wAuKSs2bJMGRCNIGenGhG2g8cTCpyxizynrz7y1Nj3Fj7Mz68RpXOclS+gvdnTWB1+YNP7cjf6ortLx2lsZHSNizLaIzxT8KcLzGB8/lqkuNbbS5QmNy5+lNs3NHd3kYMTEDAABAuuvZsL6Pmcz/RKu6U0+zogc1Xc7a99K+VxbpiIIX8cE68JbEunZpsW+jZK0LbXNaGx++S8u1Ui+2p0dxUakW22rzj9fs8pHhoweqS1XiV2svQmfv8VA9/xg9yBvW6mW/otQbNdUu0rjQcp0xMNp2xPLAzGDb2qotv6+qjbZ1Sbdr1tvWRCTJ/I40ZtUlesGmwIAHJmm4f1Xrb7phrV72j9SPH4h/v+ZmGfsWTtUb1pr6ttd6Gw/ljvR8ECAeLkf+7KvaqOHlpWHbI9siOly8owBzi/XjgmD5R4X2r5E7mxhlG9MWMQMAAEA3k/FKWYYkye+7VX7bS94uv3Nm/XiNK7P0Jq2dqjy/ZNSqr9AY84G4ypyqcZmLLO+cZe9tXVShPeX1GufrrTeC03zWmvRmAt960u+LULPeNeOBe8vLtmlvwzzNyjV7Iw4sVZ61LRqpxTWXWm8uFFVozynz2QBBBSu1p7k1+ZAzaKTkX2T73sPLPzATG1F6K/reMoYwB5dre0iu0bY9Gq9xhb213Pq5zqRHrf1znW0D0EXkztOb/o+UZ/lNT/e37mv2LTR6OUuS/L31hkZqcc0uzcrdpcXms0mWF8VYRsNaTStcpCPBz7PtNy3LyDVuOErBfbhk3U9Hb0eHRAVdXGLbg3EcPznfvHnYsFYv+2fpiWZHsr8h9raI2PitxqmoVIvX3KW8zOAE6zZm3VZv16yKlZpW2Ft55pyh/WtuhTZU9Q4/z0vXm+PEDAAAAN1Mj+bm5kCib66srNS4h6Ynsz1pLy+zt042X0p1M1zZt9B4wFj7b1K4l5fZW5I8F7NU8+J2ls5YH6lD7N3rfjHbpcWZOzQ+CYn57he75CF28WBbdY+YdUesK/eImTcNvPUGnfrky1Q3w1OImXvELDEDb70h1U3wlLq6OuXn56e6GZ6SkeoGAAAApMqZ9ask/y562aPLY1t1j5gBAAAgHZHQBwAA3daA2btaS8UBXRjbqnvEDAAAAOmIhD7aNGbVJZ1MdSMAAAAAAAAAoJvrmeoGAAAAAAAAAACAtvXYsWNHoKWlRYFAQC0tLRH/or0WCAT0+OOPp/o7eEqPHj1S3QQAAAAAAEICgUCqmwAAaaOuri7VTUCayxg+fHjCb66srNS/HG5KYnO6h6ra86lugqcUF2QTM5eIWdfC+kgdYu8eMUscsUscsetcxNs9YuYdrCv3iguyua73oB+NyGK9uUTM3CNmifnRiPxUN8FT6urqlJ9PzNyg5A4AAAAAAAAAAB5AQh8AAAAAAAAAAA8goQ8AAAAAAAAAgAeQ0AcAAAAAAAAAwANI6AMAAAAAAAAA4AEk9AEAAAAAAAAA8ICe0rVamHmrMi1/C6tT3awkqnlGxQXZKl6xN+LLh1ZkG68H/x59VU3xzOdYnvP1pzY3xt3Eps0TVVzwjA7ZpjZq26PR2wMAAAAAAAAA6F56Vi+8UfJ/ouZm48/vk/y+PlrfkOqmtZeZEC99Peoch1Zka8nWmVpWe15VtedVVbtJE44uVYktiW4sZ8nJpdoQmu+8qp4dG305FTNVv/o+V0n9MOd2a/9Racj4B5SV+FLQwYybMdmqqEl1S9KP/SaZ84YXAAAAAAAA0P30LFr1iVYVtU4omvuVCpShyt0ZqWtVEjRtLtW6oyM0Z9u7mjMs0hyNOn9S0uRi3R2aNlZTF4yQjp5Qs205M7Xsl49FTqyfe1Wbt0pDFsxtXU7hC1o2WarftTvh3vVN71aqXjM1Y0ZOgktAhzv3qlbvekhzJqe6Ienn0IpsLdGm1htotS9YfqcAAAAAAABA9xS1hv7ggVc7sx1JlzVju6pqt2tS/2hz5Cg7T9LJU7be+Ad3HbYk+Y1/25L1TmdPqF7SgNvsiffMXPuNAXec7bA496qeKrCX93H2Dg/2Gm/9m6ht51pfP7QiVikfc2SDpaTQoRVGCSH7ciP0mA6WN4pSvii8XV7ued2obWWVGl3+mLJT3ZS0s1fvbZ2pZZZRMGgnx28zbPSQ+XqbI02izdfW8iPN59wHxVpGrPe5aT/SX7zbWKxydvFuiy7L63V78cYfjvMl+zmcU9TRbN1pW3Wef8Y4v2wrtowOBAAAgBc4EvoZWl96vWoLvtLcoshvSCd3P2uW2CmYqG3n9qqi4D6jN34okdigs0clNbziSKJbLgBuG6QhEZadddtgScd1PsZFWDSHVtxnjC54xJHQrHlGxZOWakCFpfRPxUztLLVcqJm9xlvLA72rOcMOa11Z+y6e61ffp5KG+ZZlvq4llgvyps0TVVwqS/midzVHzvJFkobZSxctm2xfjlc0bS7V/vEVMW4YIWHnTunMsOPaHOOZFXBjrypKj2vONvN3t22ptLo0tA87tCJbxfuKtayNkSbR54u9fNt8GwaZv39j/7A6lGCKtYxY74u//egO2tjGYmxHtmXE2hbDXnuFhF9c4o0/pL16y3Iet2GBtG5T9OdARR7N1s221cIXLDEwzo0jdoppI7aMDgQAAIBX9JQytP7h4ANx+6is9hv53/69clPdsk4xVqW1mzRBh7Vu0iPaKWlCRfjJe/3JQVrgTJBPMnvt9H9Ao4dJOzc46u5viF67P7LXtcRMXhr1+p2jC8xlTt6k0kLL5GB5n+CFWv/H9FKk8kB5A9tXi3/YUm0I3ejI0aSSmdLRSh00kxxvrT7siJ1znhja27bOdu5VrV49mHJIHenoYM2wPtti6yP0vk5UTZV2Tp7fuj/p/5hmTD6s/e8aybS7n7U/EySaqPO1sfxWY1Ua2jflaOT4EXEuI8b7XLQf3UGsbSX2dhQS9/YMd+KMP2SPldTccFhDciOdlTOaLTLjfHnCmEhxiRVb4gkAAADvyJCuavbbn2i2OaFhfR8VZt6qgvKLenu2t8vutKVp80SVrD6sCRXnVVVo/rs0Wzsnb7IliOwPpjUS1etKX9d7NS/o7sIcTfrlJp0teEQlBUtDc02YPFM6KmXH3YN7ppaZPYGaNk9UScFSTag4b0neG6MFJpSEX2jcPWamgCI4LQAAIABJREFUtNUYDXB3fxlleSYtVX1wBsf3kSQdXWprb8R5rJxJ99sGaYhe19mzknRKZyTVl2ZrZ9gbHRftzs/VTC2r9djF09kTqtfrWlJguWmzNVtnFryrl0jyd4Cxuney9F6qm+FRTWePSyq2TcvMTV4yLbHlG2XFBpTkuFyG/X1AdLG2leivxd4Wx6p02yk9NSlb6yRZj9twg99xW4Lnp5KM87NI5xbmaLYzBdlaEpwWOpfrxttqzStap6XaUBj55aixjRlPAAAAoGsJq6GfO/sLlRdItWXXqzoVLeos517V6tWHNWTBu6GkedaM7cYw3bZ6A4eV2RmrUutQ39rzmpp7XBo2SJkJNC1rxnYtm+zo9X/OSJpHN7j15kH/x/SSdUTByUfC64BaS99sW6ohWx9pd1mTCRX2GBh/jpEGkUrueK1GqWNo97LJxncnmZ8k/R/Q6GGv673gb/Dcq9q8dYRuuy2lrUISNW0u1bo8x2ijDnwf0pO1FrazPnisbaU921HwgfXLti3VEL2uJZQDc43fcduM50CZZWFy10R/5kCM0Wzdc1s1e+eXRBipaooZW0YHAgAAwCOiPhRXBX9K77I7UR5ma0/W5+q2YVL9rt32C6mzJ1SvWAlG82G6tp797tw9ZqZ0dKneCl5I9B+oAZJ27gu/IDu07/UYNw/M0jex6vn3f0wz2qo/bXt4sOwxMNt25qz7kgR3j2mjbeiGcjSpfKnOlJr18yct1YCKWA+4hlvNDYdTtvymzRNVsushSwmv+JYR7/vQfVgTc9YbqrG2lUS2o9C2WPOM8d7aF3R3/8f0knnDnIRf/Pgdu5c1Y74mxFO+0BzNJqn7bqs1r2jd0Zm6N86bRbFja4knAAAA0MX0XJh5o70nfvX1KquVCh76Jr0T+oXFmiBn7Xvp0KalqlfwYiBYB96SWNdeVZS+Lllr7No0atuj92mdlmpBe3psF87VHFtt/rGaumBE+OiBmme0ZKtaeyPVPOPoaR+s5z84evmfc69q81ZFqdFqOrpUJaHlOmNgtK3e+SDMmmei9yozHdrXRts84O5nz9PTMNlso0yIb3tk3feQhmxd0/rbNEc8jL4vOSNK3Cz/0Ips4+Hajud8tLWMaO8DnGJtK/FsR+5+L0YpPMSH33GcnOdxNVXaGek8ydVotu6xrR7a97qGLJgbvbRQrNgyOhAAAAAekjG3PEOFmbfaJvr8n2hVUYpalCS2GpmSdPQRFW+VWuuIGg/ElaP2fVid0cIXtGHBcaO2fnCaraammcC3Xiglpeam8dC4dasrdfDcY5rU3+yNeNszKrbVqh+hOdvOt95cKHxBG85OVHHBI62LGrZUG2pbL6Azc0dIW+217IeE6r9H6WU/eZMxNDm4XNtDco22bdBElYTqtZrzOC/cnTX0HW0DkGT9H9NLFSdUbPltTqho3WccWpGtJVvNF7Zma6dGaM627ZrUf68qCh6RzGd5RJ8v1vIty7jNuHEoBffFUmh/G2sZ52K8L2b7kxlEeEKsbSXmdmQcx8+WnFdpYYxtsf8LWrYvO/zYyQ3HtrXxO4ZF4VzN2XCfiguCE6xxsm6rxmi2pyZlh5760K231XOvavPWmZpR67z5Zo1ZrNjGiCcAAADQxfRobm4OJPrmyspKDRjxk2S2J+0VF2SrqvZ8qpvhyqEV2Vqi1D0YzIsxSzVi1rWwPlKH2LvX/WK2VxUFVbo3Ccnl7he75CF28WBbdY+YdUesK/eImTf9aESW/uVwrPHwcCJm7hGzxPxoBN1W3airq1N+fn6qm+EpGaluAAAAQKo0bV4jVWynpzi6PLZV94gZAAAA0hEJfQAA0G1lzdiu0lQ3AogD26p7xAwAAADpKOPIkSNqaWlRIBBQS0tLxL9or6F7uPvZ86pKdSMAAAAAAAAAoJvLGD58eMJvrqysTGJTAAAAAAAAAABANO1+KO7jjz+ezPakvR49eqS6CQAAdGk5kkol3S/p/zCn/U7S/2f+/bukRknHJf1nKhoIAECaCQQSTgsAABzq6upS3QSkuXbX0Odp1+5V1Z5PdRM8pbggm5i5RMy6FtZH6hB794oLsnWy+VJKPrvnl5d00+qf64bXfqkeV76xvfY9GQn++yO870r+nWrp3VuSdLX/AF3N7p+U9lz7m3fjmu/z8p/rSv6dysvsnbLYeR2x61zE2728zN4cTzziRyOyuEZ1iZh5E+vNPWLmHjFLzI9G5Ke6CZ5SV1en/Hxi5gY19BN0zecX1avxpL7TfE7f+ST6yf3lnIH67Yh7deXmPp3YOgAAvOWG136pm1csVc8v3ScZr6n70PKv+JLwydRn/lxdXPNKp38uAAAAAKD7oYa+pFvee0e3vP+Orv/IGBJzfMFSfXWHcWeo5x+v6HsfHlHvD4/o+o/r9Z1Pzul7Hx5x/Rkf//dFapj1RFLbDQCA1/W48o36zS1Rr6odtuktN/TWlz97VF9O+2v9Ke8OXVP3of782FH92fmzuvY376rHlSu69vChFLXa7pq6D9Vn/lzNT3VDAAAAAABpr90ld7zqex8e0W2bN6jfO1Xq+ccrttfuXPqU/nT9DerVeFLXfH4xKZ93x/+9Uv/F8TkAAHR3fefPsyXzA9dcqy9/9qh+u+Bv1XJD79D0K/l36kr+nRGXcU3dh+p5qbVnf88vf+fotR+fK/l3quWG77U53x/zBunbvv0kSRnnzmrAqDt1Td2H+oWkC9u36PcTp7j+bAAAAAAA4tEtE/p936nSXz77RFgiP+j6j+N7eMUfMvvrD7dm64sRP5QkXbm5jy7n5IXK8Pz55xfV952q0E2Bgf/7pdDD/QCgKwmORrrp8G90/cf1yvjqkhr+ryeU+/++LMk+cqmzZXz1pW74uE4ZX13SDR/XS5L+3Cx7Fs0XI36oKzf30V90ViORkGvqPtR3t28J/fvrsQ/o01+sDSXL4xUp0X+5+MF2ty8R/eY+qlvKFumT17dEvQEBAAAAAECi0jKhf9Ph30Sdfl3jKd36r9vDXvvdncOjltK5cnMfffX9fF0aOlxf3jFEf8jsHzuxZSb4JSMJdtf/LNEt770jSZrj4nsAQEfr+ccryvvfL2nAP74adpOz+cH/M7Q/HbB5g+oXrVTLn1/TYW0JPpvkpsO/0bWfnNd3mo0SZ9FuvsYSbPcnkj559gnVL1qpq9ffkOQWo72uf/MfQ/9/afY8fVa+MoWtSczV/rfpdMMFZU59MFQC6L98ekF/dvJjEvoAAAAAgKTzdEI/2GuzV+NJ3Xj4/dD/x+vq9TeoftFKXbi/uMOSVC1/fo0++PsNGvE/fLrp8G80S1LNV1+SWAKQcj3/eMV2wzGWrMo39b0Pj+hY2Uv63Z2JPXvl+o/r9GdffSlJuubzT9Wr8ZR6/vGKen94RN8xE/gd4dZ/3a6bDr+nw//Ln7JRBojsmiNGAvzrsQ94MpkfFLjmWl1Y+0v9YdSdGmxOyzh3NqVtAgAAAACkJ1tCv2F9HxWWZUgFX6nm7d8rN1WtMllLQPQ+dkTXf1SXtJr2f8jsr0P/z5v6t40/1JJnLS8MW6oNv3xMWY75D63I1pKtlgmTN6nq2bFRXx+y4F29NCNHkpHUP75gqe796x/pWhnJpXNTHgnN27R5okpWD9ay2hd0d2hqo7Y9ep/WKXJ7AKC9hqxcFJbM/+2IH+qLET/U74YO1+/uHK7LOXka9d8eliT1ajypUf/tYX127/06M/0xfXbv/WHLvP7jOt3wUZ16nTmV1ET95Zw8Xbm5j/6Q2V/f3JqtyzkDdeXmvhHnvd78fGvJs2s+v6gR/8On3/zjv+rKzX3a3R4kx5+f+FiS4k/mV5cqz7dR8r2lk6vGR53tzPrxGld2UCpYqT1vz9OASK8FtbEsSdq3sLdK/JYJEZZ7tf9t+oGkxgMfasCoO9XrX/5Zv/vvT8b3vTxplxZnTtUblinT/Ze0vCjCrHGuN3Rz8WwnbcwTz281pGGtphUuUuTxuTG2ZwAAACDFWhP6Dd9VaZnk812V/3jqGnTLe+/opiO/0Y2HfxO1BE5brl5/g768Y6AOnvtABz41J/5gknyjjVsUl3MG6uIPx+o3/2uIlmydaUmk71VFwSMqeVSWJLolsV4bObFuJPMty6l5RsWl9+kptSb1v7ojX1/dka/rP67TLb/ZZ0voR3Rut/YflYb8/+zdfVxUZf4//hdkMq2WaGaId5BoqFkqWBr6EShX/G3eZgUrfhbz3nYXzO96088Cyg11fybsbqmrBq24UJui4ffj+FEB10gMUDJvKCnwhpG8Rc0NzYXfH9ecmXPmBmZg4MzN6/l4zGNmzjlz5pprZg7D+3qf97X4eQbzicjhuhVo0SP3E8P96gkvo/z1JLOzh24+PgjVE15WbNv1iwLDQEDt4GGGM5xEnfubLWqXVNLsVv+BuNl/IG4HBOF2QJBd+7imL3tWvjgJpc/2xTL9cp+rl/HkGwtRvPGfLWojOcYDX3wO75s3cGfQYPwc1L+Jrb9HxsShWFliw44rP8AfEoHo2KeRbfJ7RgTzgRWFNxAXCEhB6SBYDyCKAGEctujSMAbGxzw3ERYDhQ0+4vugKS1G9+kvNmtOAFdwcMk0IPMGKiKl+50wK3Ysggr36fsWsOt9Iw9my+ek6W3s/a4icCE+0S002484TgzEWAbziYiIiMhJtZOuNsU/CCRfxgJ0bvOAvlTDudf2rTYHg6QJaCW3A4JwPWQELo+MwL0HH9JnvYdgXk4akDgKG4OmYsTcCNkeqnChAsDUKFlWfASmLQ7BnrVnoAPQA0B1Vjw2Hp+Od6wE83F+M7J2AAMXLzDuJ2w13pm6DW/u24/qGOPjzr8Yi4Epy9Gl9IsmX1/157k4hel4Rz8gQM5HeVbGdJMzLMhe4jtbqr8Xgnk5uzClF/QDZNtMtmZ/t9TAlOWG29/NfR0Vc1+3uF19ex+cSHwPNWMn4onkRWZnSdkz8Cpl2Uu37+pv/9zxIdx6fBBu9h/k0HJk9e19sBzA2D9nYuj/mQXvu3fQpfQw+vxjM87+erbDnoeap8Pe/wsANgTzgbOb5mFlydNYUbgRiB+KlVa3/B4Z8cuB5GOYg3kmAf192JT4JYYlH5MFnMdiTvLTyE7cjYNrxuqDgMr9VZYDiH1Btk56zDeoAsyChP/p9ijqH+oE75s38Iv8/ejzzJO4tniZ22Xrj1lzQ9FfYxakYFjmcvzP/u8RN+cxAPa8b+TJbPmcNL2N/d9Vy8RxArFLLBwPiIiIiIicgzcAVG7qjMSSOiTMudfmDWh36yZGTQtHYMb7FoP59e19cC1kJL6b+zpK/5yJA/mnsLfkAgr2HkPxxn8aLqeWp+DiLycZgkE9YnZBW6IPCFoUgJ5BACq+Q7VhWRW+3FcqC/KL+4pgvalzZ3AKQJ/eysC7f2AIcFwMDEiqJ7yMOv1rbrzWv2k7ZM5vxuuhPRElu6QVKjepzpqkWB8VOgk5sooXxe/2RNSrm2WvW/ncOa/2RNS7+YrtX8+qMtnvUhSbPrRwqfJ5TZ7DvF1W9uMCit/tiTexFdqSC/oLg8stk49P903AFn1/blkMbNyq/wyGrZb18wVo06Zb/m6QzTpUVRgC85fCo6wG8+Xf2dDfr8P/WV9kUw392wFBhoz/4t89j84AvAB0rKrA6PA/GY7ZFfqBhC+8cvH0vJew9riVYL782GJ67Gpsnd6VZ8Px1bvvG+4HfvR+sybabTMtfL1m24WKY7hN69rQL/L3A4BNE8f2mbMPFTp55rdlIugXh9f0AWWFyjP4FkD/vsp1ffoOBJCBfXmW9vgYAoMBlJ/BWcOy75Gf+6VJ4FDp9vgXDLe97tTh4XeT0GWt684RYA95/9r6vpHS2U1jEeTfSX8Zi4xKKxvmxcu264SXN31v/z6cgC2fk6a3ad531dTZTWuQjaexYgFLQxERERGR8/IWpXbaITbzOtQ4s7RjVYVZfeVrISNR/noSjqR/hn1ffIfijf9ExdzXceXZcIdmbw5/YyvGH0/CrNBJyDmfj7TQUSIb31AbvxLnjgOoXG8SRJcFyHv3w0AL++7ROxhAOS7IXlp9ex9o9bcbC+gXvzsKG4+HYN6MCOWKwqWImpKEPmnK4OaeeFlA5vxmrJUFRrUln2Pek6XYmNhI4McGp9aOwqzKBNk+t+FNWTCpOmsSouKBd+TPiyTMMg04PZkka9sFcSZDY0Epp5SPL3bIPyfUchGIl80VoassxcBAS/+1VyFnyzaMH8O+bwnp+FPf3genllsLMpoPsvw1+wtUT3gZR9IX4f9BCP743l4xqPpOHOLQH++980/sLbmAzz8twInE93D2132R+JfreCVH/53PSQLWxisGGKVj1ryp1lqbj7Qt/fTtEMeVtYYAdGPrlC6FRxmy8n2uXsZD35y0t9vaiCNebz7S4ssxz2K/W1q3vs0HVr3u1OH+ClE//3bUrxyz08oP8IfELxGdmWY5eFf5DY7iaQSZHloCH0djQ1Rj1nyK6JLleM5/LDIq92GF/1CsLInDlkZqwV9a9wGuvpGEBh+NYZnvX1PhdafOnlfkQsSZEUdDUzCHZUpaaB825U7BAd0NVOhu4EAysHL9PovbrYg9hRWFYruKwhQgMQ0H7dqHe2nOd1VJGgBYwkEoIiIiInJq3nnrH0RJ7HWsUekfMHmWZPWEl3Eg/xSKN/4TZ389u8ks0JaLQHzJVoxHKTZOmYE9AManmWdan6roh8WmAfIp+szyXs9j9JPAni2bFZn+OVtMS4QIB/XXHaq+M1mzDW/qBwzerEjCFrOzC/T7nLoV8WGyxWGr8c5U4JQUkOk1G+9ZmkQ3qG/LavE/mYQthgB2AKbMmg4cz8WX+gDRp2tLTfrOdJtGtLRtbe38dzj7ZDmy5IM8sjMaqHnk2eBvYqth/gmFwvXYiCRMCzNfRba7X382VGXca41MENvIIEuhFnumJiD0vwbhWshIXBu/EkFTv8WW2u7KXei3MxzLes1GzNRSHPpcCkJXIScxF6OTZ6On1dbK2xGAp8eG2LjO3Le/XW54vY2fJaUmB7zeJvtdffddEhPc/BzU36aSO7Y4uH45jsZ+2gqTWI7FSt2niMaXWBkmJoG1OmggU/vbRTh75Dh+enYUADGI4XPia0c3TkXfI2OilAGuD5xam3yU7DAWK2X9WHXmSwzr11eFfbii5n1XDfLSsLIEiI5idj4REREROTfv2Mw6ZK5RP2Ps1PIUnEh8z6EZ+E0RAcQZQJqUgRqCPfHmwdmBY+UT0+oD1diGLwr19z+UMv2lAO8onAuaDiAYPU1K/pTprzucNQ3oTzdkt28Zm4tZZqV0xNkCljKTh4+ZDsXZAIqyPKOwMWgrtKbZ5Ir22hCQNg269+6HgSjFuXMQAW5A9J18n2Z1z82f901XzXQ/HowYwyDPVozfMcOs9BHZR5TJ0n8HAlMtlBPRZ+fPsjKfBdlNmjzWGmuDLNXnzCda8Q80Dy43tV11VjwOjU1rpDSaKVGOzLTEWdPrhPr2Pqj8zWu2PpkTaN7rbbzfIxCfMwGHpuiPw1POIEaFkmHtLv0AwCQ736R8SJB/vGEQvEl58WIyTJszcW0nSpfoJ4DV3cCB5KeRHdsJQUuaznj+T7dHcXHbdsOgRbsL5xzePvU8hrjP9Nnhuhs4kHwKs0zKvlDzyMvlzMKn+MRSCSmMxcrCKfifMP33JewbvKYzBq9t24d7acl3FfgeGakZAM8yISIiIiIX4A1oEOvfHf76S1hiO6DkQYT5d8fETe1avQE/dRd5mW0ZyAcgyjysLcXAxZ8bMt57xOwS9bmbCs6aldmJQLy8xnfJBUwLLAee7Ad/k4dKYRafq5es7r5HzC68M9Uk618fNLdONnjQazbek59RUDHDvFa9vPRNThIG7pjR4izz8WnKPhAXkzMNLJXccdE6+kYReNZquRBqjh4xCRhvenZH4XpsPD4dzzI732GsZ+cLTQ+ytMD5zVi7Nhgxdkz8XZ0Vj41BJmcp2bBO7sqz4XY2tHXJB01Ma9k74vVafE5p0vWcJAzENrypwhlGXnfE2Xl3+/YzLoxMMwSHxcX2zNqD2gwAGZglGxB4LvFLoGQ5npOCzIGPYxi+RIVpLXFrpXgAQxmfYcnHDJn/febsQ0VmHJA5DSss1t1XavDR4MaMmeJ116mfQNFa+szZiBWhwFFD2RdqLlEvXh+U7rcGQRM/sPgb8Oz+HBxFHLYUpmAYMjBLFri2dR9uo6XfVSk7P4FnmRARERGR8/PW6S5CfilMvgeE3kKh7iI+a8NJch9fm4SuXxS02fNZm8xWGawPRO8ngVP79iuDWOfO4BRC0Lu3tZ3rJ9NVZPYLNRCDFw/oLjTavOFjpgPHk/CpNLDQqy/6ANhz0DzwUnxwm8XBA0E6o0BZz1+h12zENBWQVkweDGUf6Nt29pz95RzMzi5wBb2ex+gnpTM0AJzfjKwdjX0eqEmFS5UDSoVa7DE5w6X44LbGJ6gmuzV1HJKzOMgio6sstWk/hu3OncEpeamxHVDOB2KiOmsSZu2bICv9Zds6U/XtfWxqZ1uRD5rIy0w56vVKDP1euFQ8tmQ1hveajff0g75qnWF0r5djQmdj1twwGQwQ2bkITcEB3Q2RnRzYD/0BfPudMoP87HenAAyExWk7Kr/BUZhPpNtU3X1Td4Z50JEr9HHYPkxHTekzZwmiS3KQbzoQlReP53Kn4IAuDWMCF+IT3TGsKLccuLa6D3fSwu+qGBSMw1hm5xMRERGRC/BWuwESn6uXEfL7WIT8PhY+Vy+3/hOGRWE8TGvfA8Vbk3AKUhawVAdeFlhHPtLitwHy+sQKVch5dRQ2IgmLrWSe/tS9l2LuAMvtW4B5itr8EZi2OMT87IHCpXhzB4xlSEwDo4Z6/ublfwzOb0bWDliZhFTveBJmGfZr2geibadMJ7ssXNpkRm/xwSba5pQCMCU5CWelEkNTktAnzXTOA7JL2AL9mSRSuSbgHXkZkPObkbVjul3Z3NQ03xNHra9sZJClx6gJGLgj1fh91w9qjR6lfH8a3S5steJsnnemirN8LM2dUPxuTzEpt4X5QRpb56pa+nptfX8E/eTvKmnbSWLHYmwscDRxHjKkwKYhqzfeeDZAXjyC/MeKbSJfQDSA7FRldvPB9ctx1I7g371ujzrqRTiJfVhhWhJJn+E8bEIUM5xbIi9eWSImbzeyrQ04KXyHipKW7sOF2fpdlX+/JZUf4P1MKI8DREREREROrPVr6jTh5wc7ob69jyHA3fWLAoyaNgbVE17GrX4DcfPxQbjVf5Dd+63OmoRZa2UZo8dnIGoHIGrVr8Zw/YS4CJ2BWaFJskdOVwYSw1Zjy+JyzIrviT3SsqnymvT6AL48IDLVQs16mTtdH0G7H2828QrEhIcb1+biy/OzMaWXPpOz91JEyduCEMzLuWAMJoetxpZz+rkBJE8mYUuJMfjjHxgC7EhSvO6Biz/XB9KsZNlP3SpKbkj7VUySK9q2BZMwa0pPbJQ/r2nQ6bjyeU3b5jJ6zcZ7JbPVboUbCcCUDy9girXVvWbjvRJrK8ledx7uBgDouX0rvo97zXLWetgCzNsyClGh0gLZsbHXbLyXdgZRsu/7+DTpOJSPNP3cJPFhjW3XGNk+eosBR0A6hsvacr6RdVb2/MBF289KUEVjr6nR1yv+Fp2b1US/91qNdw72ND/+q1TKSnO0GP+OeL7J7c5uGitK6EhKpiEoEwDisMWO0jxj1tzAFnTCrLBOWKlfNiz5mKK+uMjYl4hJNuE/Dc/5L5ctt+953c9YzEleg+f8OymWRmfeUExK7Kj3zaNExmNF6lAEGU67lPfV98iYOBQVCTewMjINW7SdFJ/LYcnH8EkkADS2D+djy+ek6W1s+64qv9+CFPTf4gHzDBARERGRe/DS6XQNzX1wbm4u+oT8qukNm9Cl9DCC1ybhwW9PWt3mWshIXA8ZiZ+698RP/r1QO3iY05VOsEVUaE9cmPAyupQexr8+O6x2c2xS/K6YELOxQYrWFBXaE9oSJw/CORn2mXNxtvfjAd15/NdEMSHu2V/PRvnrSU08wnWZ9v0Tya+jR+4nOJH4HqonvKxiyxwtH2mhWjzrgAluo0J7okJ3wyGtsuaBLz6H/7Rf4T/dHsXZI8fR4KNp1eezx8ElnTCrPAUHPrO/lnaQfyeLfedz8mv0HDsKl9Z9gFuvTHdMQ92Mtb4juX1Y4b8bYx0QnPfU/m7p99uZ/paTdeNCemBvqcNm/fEI7DPXxPfNfuwz+7HPmmdciMulrarq5MmTGDTI/mRuT6Z6hj4ggvVf/GMv+v81BYEZ71vcpkvpYXQpVQbArzwbju/mvI7awfZUsiUi8mw/+ffCnYcfgc/Vy+jzj80AgMrfvNbkJLmurkfuJ+iR+wkA0QfupDorFUjb5TJzTNzrJs4Sue/SD3j43WRcSU5RuUWSfdiXCURnOnZizE6b1wNw3JwB5JnObloDZO5z2kx759c6328iIiIiorbmFAF9ybe/XY7zU2PRpfQwOp04Bt+vjzaatd/1iwJ0/aIAF385CWd+u8xlAjT332qq3A4RUes6GzMb/f8qgqh9/rEZff6xGRd/OQmXw3+JOw93w83+g3DvwYdUbqVjtLt1E4999L5iwPhnN3ltkh4xuxCvdiPs8HNQf/yn26O479IP6LTpA9we9yv89OwotZuFs5vWIDv2U1Q4aGJMrzt16LRpPR78eJtjdkgerc+cfYZSUWQ/R3+/iYiIiIjU4lQBfUBkTVb79zKUQvC+e0cE9r85ift/vInOpYfx0Lcn0U4WFO/+v7vQ/X93oXbwMNwYPAy3+g3ET/69nDYg1dgghTMa/sYFaNVuBBE51Nlfz0a3g3vh+7VxYlzpWCqpb++D2sHDcD1kJK6FjHTKUmftbt3EQ/pjartbN/DQt6fgffcOOn19FB2qKtAuWrzzAAAgAElEQVQAABEDFY+pHTysWXOzkGNdfy0BXRNFretHF76Kc/8qRv1DnZp4VOvqM2cfKhy0L01pMR5d+CranT9nWNbg41zfHyJP4sjvNxERERGRmpwuoG+qvr0PrumDSXI9cj9B303r8IDuvGGZ79dHFcEpALjz8CO4HRCEW48Pwr2OyuD+zf4Dce9B68GD1gheLYOoX+0qZxMQkXuqb++D0j9n4rGP3kev7VsVg6QS77t3DOXO+uofc+XZCFwZOQZXRoabHcd8rl7Gk28sRPniJIcFzH2/Pgrvu3cMwfp2P97Eg9+cxAMXLyiO/7b6yb8Xjv/Rcmk3als3//tVdPxsBzSlxbjv0g94dMGruLhtu9rNajGvO3Xo+s6beOjDvymW//TsKNSFuEpRJCIiIiIiInJWTh/Qt6Z6wsu4OG4SHst4Hz23b4XP1csWt/O5ehk+Vy+b1d+3lZShejsgCHdl9aVvB/TFnYe7NfpY6awCjT7w1KX0MMbJHk9EnqGhodlzj7eyHkD4X4H1/x+QnQ3s2gXU1gI1NUB5udnW3nfvoFuBFt0KZOfsDBkC+PqK23V1QGkRnl2z1LjMHnV1QFFRM19L087+ejYq5rzulGdueaIGHw1++OBD9P6v4fC6U4df5O9H18TlTlRPv3H3XfoBHXdth+ZoCe67/AMA4DCAxwIfNdv2dtQLuJT6QRu3kIgcyXn/lpMlnIyQPAU/60TOh99L+3FCXPt57d69u6G+vh4NDQ2or6+3eLG2rqGhAXPnzlX7NQhFRSIA9dVXQFkZUFUlLk4qGUCS2o0gojbhskGAoiJAqwUOHhS36+rUbpFl8kGFIUOATp0APz8gOBgID4eXl5e67aNGxQFIl91fAGCDSm2xVQKAFAAaG7Y9D6A/ACf99hCRjVz2bzkRERGRCzh50rXKk6vNS6fTNfvXaW5uLvqE/MqR7XEoqf6+VKqhKVIpB0Bk9neoap1Km4cGR2DDCwm4renYKvt3NzvfisTkt/PUboZLYZ85l51vucEMfHV1Iri/d68YPC0oaJvnlYL1Gg3wzDNi2YgR4r48kN8Ifhfso8bx4/c71yDy2F7D/T9PXoK8oeMaeYR65u9ORVRxbpPbXXvwYXS5dRUAkDd0HP48eUlrN82l7Up8DtqSC2o3w2NEhfZkf9uJ2Xbk7vaWVqvdBLITj0vNw8+6fcaF9GCf2YnfTWoLLltyxxZS/X0AuBQe1ax9SPWbfa5eQoeq78zWt7t1E32yNgMAbgwehisjw822+U97H9zQ1+N/Jm4C1jK4RORx3COo/BDQ/SWgO4CIN83Wdqutwd/WTcfaaStwaHBE6zXjSwCoB/51tKkt3WMwxQNseCEB3a7X4ImqrwCIAH/7e3ehHT5B5ZYpRed/pAjm39Z0xKHBEfgyOAzXO3bGug/mGr7rnX+8ho3rpqP9vbuIPLYX99+7i79MXoK77dqr1XwiagEvLy9MSj6gdjPIBkxssR9/L7kuftbtw886tRV+N+3H76d93Dqg7wi1g4c1ut777h34/e8u+Fy9jE5fH8XJ5SkOmwySiMgV3X/vrtpNIBdzt117pMS8jZXpixFYI86Om787FU+XF2LDhARc8vVTuYUimB9d8HfD/RMBTyEl5m2rZ9td79gFH4f/N2bsF4P+o7/OR+DF7/CXKX/ANz0HtkmbiYiIiIiIyP14q90AV1ff3gdnfrvccD8wg5PeEZFn6/zjNbWbQC7otqYjVsxci0q/IMOyYRXF+Nu66fj9zjWGQH9b61Zbg+VZbymC+UeDhuPtGauaLJ23fXQMjgSHGe73vHIOqzf9DrO0H/B7QkRERERERM3CgL4DVE942ZCV/2iBFu1u3VS5RURE6gn4wbw8GZEtpKC+aQZ75LG9WLd+Hlamv47IY3vRvg3OAnmmvBCLP12Jv62bjmfKCw3LK/2CsPalFTaXzln70grkjnxRsWzC4e3YuG46ZuzfjA51Pzq03UREREREROTeWHLHQb5Oeg/P/nocvO/ewaMFWlRPeFntJhERtSmpLMrj50+r3BJyZbc1HbF0zl8w4fB2TP08W5HJ/kTVV3ii6iv8fucaVPoF4bamg9njTwQ8pbwfOKTJ5+x2vQbdamvQ4c5tBF6sMNTyN/VNz4F4e0aKXZPa323XHluiFuJY0HD8LmeN4fW0v3cXLx7KQlRxLnaMikbuyBdZX5+IiIiIiIiaxIC+g9zqPwjXQkaiS+lhdD5axIA+EXmk25qO6FYrgqPOUPecXFfuyBeRN3QcIo/tNQvsA7BagscsGC8rldNctzUdWxx0Pxo0HL/9XbphoEI6y6BD3Y+YsX8zXijagb2hLyB35It2DRgQERERERGRZ2HJHQfSvfASAKDrF/kqt4SISB0XuvYGAAw7U6xyS8gd3NZ0RO7IFzFv0TasnbYChwZHtOnzHw0ajg0vJGDuom3YPjqmxRn0tzUdkR3xG8xbtM2sDE/nH68huuDvSP/TS5il/QDdamta9FxERERERETkntrlLfFHbKb5ithMHdZE2r/D4nd74s0dAKZuhfYN5T/e1VmTMGttqcV17uDiuEkYmLIcPlcvo0vpYVwLGal2k4iI2tS3vQbg8QunMLSiGNrhE9RuDrmJu+3a49DgCBwaHIG101YYlre/dxf9LyhLPEnlcyRSGZ3GXH+wC6of7gUA+LbXQNxt196sdI8jXe/YBVuiFiJ3xFTM2L8Zo782JgK0v3cXEw5vx4TD25E3dBxyR0xVTBRMRERERERtrzprKdau3YZT+vsDpyZh8Ruz0UPVVjm3gIgn8IfR3Qx9VF1ehT998j2qVG2VexAld0KTUfjZHAS25jMVLhXBfDdW394HtYOHoUvpYfj972cM6BORxzkSHIYJh7ebBVmJWoPFwHsrBuId7ZKvH9ZOW4Gtz8/G1M+zzSb8jTy2F5HH9uJo0HDsHvkijgYNV7G1RERERESeyZC8LHNqRxJmVQBbPmRQ35IxL0diUbByWY/gAKQuBBI+YFC/pdqo5E4+0uK3tc1Tqey6PojfrUAL77t3VG4NEVHb+rbnANxt1x6df7xmVvOciCy75OuHDS8kYN6ibcgO/2+zGvrDKorx1tZlWLd+HiKP7VWplUREREREHuj8ZmTpg/nj0z6HtuQCtqRNFwuO5+LL8+o1zVk1PPoYXtYH84/sOILJb+chYcclsaDrIxj9qHptcxdtEtAvfncG9pgtrULOqz0RFWrh8upmVOu3qi5citcV201CWla+YT2QjzSzfUxCjkpfqIu/nAgA8Ll6mbX0icjjyDOmWQOcyD7XO3ZBdsRvMPMP/8SWqIVmE0sH1lTg9zvXIP1PL2HC4e3oUPejSi0lakWFS8Xv+Xct/I4+vxmv63/vv55VZXG52TqZ6qxJiv8ZzLZr7LmJiIjIM507oy+zMx3PhgUAAHqERWE8AKAU586p1jLn9cgv9GctXMIXJ24DACpPXMYRAEAH9HxEtZa5DRHQL0lEmL8//PWXiZsqHfcMhUvFaSlPJmHeVPseWp01CbPit+HUcfnSUuxZOwOznPSH9u2AINwOELVu+2RtUbk1RERt79ueAwAA99/7WeWWELmmu+3aI3fki5irnwzYtIZ+5x+vYZb2A/xt3XTM0n7As2HIbVRnTUJUI2f1Fm9NAqZOx0DF0nykTUkCFusz5haH4NTaePPknvObsXZtKcanXbC4XVPPTURERJ6p+ly5uPFkP/gblgai95Pi1tlzLB5jKvCRDuLGlX/jrGHpj7hwRdzqKa2nZvOOXKODTme8FCaHoiQxzEFBfanUTgjmJc9GT8W6AEz50PiDGoCYLLfkArQfzkYP5ONTfc39gfof6Iptd6Sa/FAPwbycC/rtdmFKLwc0v5mqX3gJANCl9DAe/Pakeg0hIlJBZXcRfOx8i0FGopY6NDgCixZsxIqZ7+FIcJhiXYe6HzHh8Hak/+klvLV1mWJyXSLXU4Uv95VifNpWfcabicKleHPHdMTM6GeyXIs9CMHoUfqMuVETMBClOPS5yT/X+uw6y/90N/HcREREREROxKzkTuCcz5AZC5Tk7kfLQvrfIedVUWpnfFozAuyFWn2ZnumIiQkwLO4Rk+D0p7XoJryM+vY+AICBKctVbg0RUduS6n+z5A6R45wIeAopMW/jt79LR97Qcbjbrr1i/bCKYiz+dCXS//QSZuzfzO8fuSCR7BMfZmldFXK2bMPAxQtgOjW0IWuuKWGr9Vn5oxAV2hOz1pbK/kdp7LmJiIiIiJyL9Rr6JWdaFtDfkYSNxwFM3epxP47vPPwIfgiPAgD4fn0U3Qq0KreIiKjtXPIVM9z0uMrZgYgc7ULX3vjz5CWYt2gbto+OwfWOXRTrO/94DS8eysLf1k1n1j65jeqseGw8rkzysZ/Iwpfbs2WzbF4uIiIiInM9eutndz1+BjrD0kqc05cH79O7Jb9P3FPlZVE3H11/gT6GpR3Rs6u4dUFaT81mIaBfie/KAYT2Q2CLdz8d77wR0byH9u6nr4+5DVmyCauqs1INmfvPOvFAQWXcQsPtgSnL4X33joqtISJqO1KG/hOVX6ncEiL3db1jF2x9fjZm/uGfWDttBY4GmeYtG7P2t6VMwvzdqeh5xUlPbSRqgq6yFMA2vBnaE1FTknAKwKm1o6xOfmuJGBSQlehMmw4cT8JaO/ZBREREHkgWn/yiUPxuqDZUFQlB796qtcx5Xf63PmmiG559QtTLD3ziETwDALiNC5dVa5nb8J44cZMiE79yUzwSS4DYhDktDuiPT1ttdlqszXrNRox+El3p1Fjp9FgAFk+5dSa3+g/C+RdnAAB8rl5G0N/eU7lFRERt47amI25rOqJbbQ3LfhC1gUODI/D2jFWYayVrv0Pdj4gqzsVf/zIT69bPQ1RxLifSJZcy/I0Lhvm0tDlJGAgxx9Z7MQFmNfOrP8/FKamm/vnNeD20Z6OBf2bVERERUaNk8ck98frSffHbxIKpCarO4emsvH74Hp/oqyI+M/UZ7HwrEqlTu4kF5VXY+oN6bXMX3hOQiDB/f/jrL2GJwcjU6bAmsmU7HuiAUjvD3/gc7yyerh8J03syBOPTxA94Z/fd3NcNtfQDM96H79dHVW4REVHbqPTrCwAYdqZY5ZYQeY5Lvn6GrP23Z6zCocHmZ0kG1lRg/u5UpP/pJSzPegujv85H+3t3VWgtkakq5LzaE1GhYg4u7JiBqNCeSCts4mG9ZuO9tOmWa+PrJ8Lt0zsAPWLSMO/JUmycIpKEouK3yUqDNvO5iYiIyCMMf+NzzJsaIlsSgvGLP4e2uVVJPEDBJ0ewvVxeWuc2jhw6gsmfMJrvCO3mfKbDHAfucPgbF6B9w751PWJ2QRtj6REBGB6zGsNjVjfyjBGIL7mA+Ga0tbXdefgRVMx9Hf3/mgIAePL/fQ2IHqtyq4iIWt+JgKfwRNVXGHUiH9rhE9RuDpHHORo0HEeDhuPDqIWIPLYXEWX/a1Zy55nyQjxTXojbmo44MiAMeUPG4UTAUyq1mEhMTDulqc16zcZ7JbOVy8JWQ1ti/v+CmDBXKtPZ2P5tfG4iIiLyUAGY8sYuTLES7yRzXriNrZ8cwVa1G+KmrE+KSw5x9tezcTsgCADwgO48sGCByi0iImp9JwKHAACeqPqKdbuJVHS9YxdsHx2D3/4uHUvn/AXa4RMM81xIOtT9iMhje7Ey/XX8bd10ROd/xHJZ5Aby8ena0paVACUiIiKyUWpaKVLTStVuBnkIBvRbWX17H3z17vuG0jvIyMAz5Tx/l4jc27c9B+Buu/YAgHElu1VuDREBwDc9B2LDCwmYvnwX1k5bYbEkT7faGkQX/B1/Wzcdqzf9DpHH9qJD3Y8qtJaopfRn8bawBCgRERERkbNhQL8N3Oo/CBVzXzfcn5+bysnoiMit3W3XHp/rg4XjinNZo5vIyRwaHIG101Zg+vJd2PBCAir9gsy2efzCKfx+5xqk/+klLP50JYZVcE4MIiIiIiI5ZuaTGhjQbyOVca+hdvAwAEDnH6/hdzlrVG4REVHryhsyDgDQ/t5dRB7bq3JriMiS25qO0A6fgEULNuK3v0vH9tExuN6xi2Kb9vfuYvTX+Xhr6zKk/+klzNi/mSV5iIiIiIiIVOK1e/fuhvr6ejQ0NKC+vt7ixdq6hoYGzJ07V+3X4DqqqoABA4C6OnE/MRFISlK3TURErWnoUKCsDBgyBDh2TO3WEJGttFrg44+B7Gzj7xZTI0YA8+YB0dGARtOip/Py8kJDQ0OL9kG2Y3/bj31GREREtpr8dp7aTXA5f3zxUbWb4FK8dDpds3+Z5ubmMqBvp+o//hE9VqwwLsjPB8LD1WuQCzh58iQGDRqkdjNcCvvMuXj0+7Fhg3Ey8GPHRGC/DXl03zcT+6z53LLvamuBnTuBjz4CCgosb6PRiKD+vHkiyN8Mbtl3Toz9bT/2mevge2U/9plr4vtmP/aZ/dhn9mOf2Y99Zj+W3GljtZMnA5MnGxfExAA1PG2diNxUXBzg6ytuf/SRum0hIvv5+orvcX4+UFkJLFsGBAQot6mrAzIygJEjxZmIGzZYz+onIiIiIiKiFmFAXw1ZWUBwsLhdUyOC+kRE7kjK3AVEwI+IXFdAAJCSIgL7e/YYv9ty5eXirJzu3YFFi0S5QSIiIiIiInIYBvTVoNEAOTnGerMFBaylT0Tua948cV1ba71kBxG5lqgokaBw/Tqwfr0xUUFSWwukpgKBgcCUKaImPxEREREREbUYA/pqCQ4W/wBLkpMZ6CIi9zRkiLF2Po9zRO7F1xeYPx84fRo4fFiU5zG1cycwfrwox8MzdYiIiIiIiFqEAX01xcUp//FlPX0iclevvCKu9+5Vtx1E1HpGjADS04GLF4HERMDPT7m+vByYOVNk7bPOPhERERERUbMwoK82+WnqrKdPRO4qKkpcFxWJUhxE5L78/EQpwYsXRYB/xAjl+qoqUWc/MFCU5WFgn4iIiIiIyGaGgH7eEn/4+8suS/LUbJfnYD19IvIEQ4aICTUBEdQnIs8QFydK8eTnGwf2JDU1YuLcwEA8vHUrA/tEREREREQ28AYqsWmiP2LLk1Go00EnXdZEqt02z2FaT3/1aqCsTL32EBG1hvBwcc2APpHnCQ8H9uwBjh0DJk9Wrqupgd/q1aLGfna2Ou0jIiIiIiJyEd6Vm+KRWBKLzM/mIFDt1ngyeT39ujpRY5aZakTkTsaMEddffaVuO4hIPUOGiDMTT582n0C3qkqUHhw6FNBq1WkfERERERGRk/Pen1uC0OQFYD6+E5DX0y8rA1atUrc9RESOJGXoFxSo2w4iUl9wsKivf/q0ecZ+WRkwfry4lJer0z4iIiIiIiIn5X2mBMCZ9Zgor5/vPxGbKtVumgfSaICsLGM9fZbeISJ3EhAA+PqKSXEZpCMiQAT2c3Lw/bZtxkE/iVYrsvWTknjWIhERERERkZ43AJSU90OaoX5+IZJDS5AYtgScFlcFQ4YAS5eK2yy9Q0TuhnX0iciCn556Skycu2eP+C0kqasDkpNFYJ9n9xAREREREYmAfuiE52X18wMxJyEWQCa0jOirY9ky4z+zZWVAaqq67SEicpRnnhHXBw+q2w4ick5RUWLi3PXrxRk9kvJyICJCJDrU1KjXPiIiIiIiIpV5W1wa2A+hbdwQktFoxD+ykuRkMVEcEZGrGzFCXO/cqW47iMi5zZ8v6utHRyuXZ2QAAwYw2YGIiIiIiDyWd79QoCR3PxQl8yvPoASh6Bdo7WHU6kaMEJn6gDjdfNEiddtDROQII0aIQcvaWs4RQkSN8/MTcwvt2SNq7Utqa8XvoqFDWb6LiIiIiIg8jvechFigJBHrDeV18rAkNhOITcAcBvTVlZgoJpEERDYrM1qJyNVpNMYsfdbDJiJbSGV4EhPFMURSVgaMHAlMmcIBQiIiIiIi8hjeiFyDwuRQZMb6w9/fH/7+sciMzYRuTaTabSPT0jsLFnCCXCJyfWPGiGvW0SciW2k0QFKSKMMTFaVct3OnyNafOZMlComIiIiIyO15A0DgnM+g0+mMFwbznUdUlLF+bE0NsHy5uu0hImopKRjHDH0isldAgCjBs2eP8SxGSUYGEBgoyvFw4lwiIiIiInJTlifFJeeybh3g6ytup6YyCEZErm3ECHFMYx19ImquqCigslL8RvLzU65LTWVgn4iIiIiI3BYD+q7Az0/UjZXMnMnSO0Tk2sLDxXV5ubrtICLXlpAgAvspKcbkB0D8TmJgn4iIiIiI3BAD+q4iIcE4kWRVlainT0TkqqQ6+keOqNsOInJ9Gg2wbJkI7CcmWg7sDxgArFrFhAgiIiIiInJ5DOi7kvR08U8rIOrE7typbnuIiJpryBBxzZI7ROQovr5i4tzKShHgl34zAaLE1/LlIrDP309EREREROTCvHbv3t1QX1+PhoYG1NfXW7xYW9fQ0ICwsDC1X4NHeXjrVvitXg0AuNe1K7779FPc69pV5VYREdnnvlu3EDxyJBp8fHD6iy/Q4OOjdpNI74knnlC7CUQO4QdgKYD5ADQm64oALNJfE9nqxIkTajeBiIiIiAheOp2uobkPzs3Nxdy5cx3ZHrd38uRJDBo0qGU7iYgwTowbHg7k57e8YU7MIX3mYdhnzoXvhxUDBoga+jk5wOTJrfIU7Hv7eXl5AUnW11fMvdF2jXExQf6d2HfNFOTfCRW61umfdufP4eF3k9Bx13azdbdemY4rySmof6hTqzy3s+Jn1X5B/p3Q0NDsf5uoDfFvv/3YZ66J75v92Gf2Y5/Zj31mP/aZ/VhyxxVlZRnrwxYUiMneiIhcjTQvyK5d6raDbMYgX/Ox79Rzr1dv/LD+Q1Tn7kddyHDFugc/3oY+Tw/Ggx9vU6l1zoefVSIiIiIi58aAvivy8wPWrzfeT01lPVgicj3SxLjZ2aK+NTk1Bvmaj33nHOpChqM6dz9+WP8h/tPtUcNy75s30G3RQvhP+xXur/hWxRaqj59VIiIiIiLnx4C+q4qOBhISjPdnzgSqqtRrDxGRvcLDxXVdnZjom5wWg3zNx75zPj9OehFnjxxH7W8XocHHWF3/gS8+R6+xo+H713XwulOnYgvVwc8qEREREZFrYEDflaWkGEtW1NYCMTEiMEZE5AoCAozHsI8+UrctZBWDfM3HvnNeDT4aXH0jCef3HVKU4fG6U4eH301Cr7GjoSktVrGFbYufVSIiIiIi18GAvivTaJT19IuKgClTGNQnItcxb564LisTE+SSU2GQr/nYd67h56D+qM7dj0vrPlBMjHt/xbfoMeF5PLJsEbxvuvd7yc8qEREREZFrYUDf1QUEADk5xvtaLYP6ROQ6oqONg5KcC8SpeGqQ7+ymsQjyj8fBFuyDfed6br0yHef+VYwfJ72oWP7Q3z9E7/8ajl/k71epZa3LEz+rrvw5JSIiIiICAO+J/v7wt3JZkqd288gm4eGi/I5EqwUWLFCvPUREttJoRFAfAPbuVbctZNDsIF9evCJQdnBJJwQt2WdYLQJpnRSXlzd9r9iF9WDbPqywsL3wPTImiv2tMPvtYu1xje2v+dh3rus/3R7FD+s/xMVt2xWT5t536Qd0n/4iui1a6FbZ+s36rPJzSkRERESkOu/PdDroTC6FyaEAYhEVqXbzyGbLlomLJCNDTJRLROTsXnlFXBcV8ewiF3f2u1NA6OMIAAB8j8pyYFi/vvq1+7ApcSC26G6gQrpkxuFo4tCWB9zy0rCyJA7RsUC2dl/T2zsh9p3z+HfE84ZJc+Ue/HibW2fr24KfUyIiIiIi9VkouZOH9YklQGwUGM93MSkpQFyc8T6D+kTkCsLDAT8/EcxnHX2XVnXmSyC4H/rIlvXv+5j+1lis1KVhjPwBkfFYEQoczdXibAue96A2A4h9ASuj4oDM3S5ZSoN951ykSXOrc/fj56D+huXumq1vK35OiYiIiIjUZxbQr9yUikyEInkBw/kuKT3dPKg/fjyzXonIuYWHi2sG9F1T5Qd42b8TZmUCyJymL7UxFCtLgOxYZUkOpe9QUQKzAKF99mFfJhAdNRaIfAHRyMD7rlRig33n1OpChuP8vkNtmq2vLFszFhmVVjbMi7da2sbmfdiKn1MiIiIiIqdhEtCvxP7cEiA2AXMC1WkQOYBpUJ8T5RKRs3vmGXF95Ii67aDmCVyIT3THsCIUiM7Ul9ooTMEwPI0VhTdQsWasxYcdXDIN2XgaKxZYXm+TvN3IRhzGRgLAWIyNbXk2cJti3zm9ts3W34dNuVNwQF+y5kAysHK9pWD5PqyIPSU+I/rPDBLT9Jnrtu7DDvycEhERERE5DWVAP289RLUdZue7PEtB/ZEjgdpa9dpERGTNiBHieudOddtBLaDPxJVUfoOjGIhAeYKASUbxrMw4bNHtQ5xZEkEGZplMrBnkPw3ZZs/5PTJSRSkOqczHmKg4oCQH+YaMZH0AMHFey7OUWw37zhU0la2vKS12wLOMxcrPFhqy2avOfCmrUd+W+7CEn1MiIiIiImcgC+hXYlNqJhCaDFbbcROmQf2yMmDoUKCqSr02ERFZMmQIoNGI41NZmdqtoeaoPINv8TSC5IE7w+SZepFpxskydTdQkQkR1DMr1xGnnFhTdwMVuk8RbfacWvxPib4Uh+E5XkA0vsT/7DeW5Biz5ga2xH6JlWFNBQ+BPn0HNufVtwz7zmU0lq3fY8Lz8P3ruhY/h7xczix8ik/mPGZhq7FYWTgF/yO9L2Hf4DVZ/Xrb9mEnfk6JiIiIiJyCMaAvZecnzAGr7biR9HQgIcF4v6pKBPUZMCMiZ6LRAMHB4jbr6Lucg0s6IShsOY5CFlCLzQBKluO5xup3R6ZhSyyaPcnl2f05OAp9DW+TIN5RQ/kRYcwaG4KHEtMgZSti37kma9n6D7+bhO7TX8R9l35o9r77zNln6OsD/R0qBA0AAB/TSURBVNYgaOIHFsvLiPcwDlsKUzAMGZglC5rbug9b8XNKREREROQ8DAH9PG0mgFiw2o4bWrdOXCS1taL8jlarXpuIiExFRYlrnkXkcsasuYEDyU8DoSmGut1bYgHEfooKi+U2HOF75Od+qX8Ok0BeZhyADOzLa8ZuI9NQIStX0trYd65LytbXffp/8Z9ujxqW/yJ/P3r9cjQ6aHe3+Dn6zFmCaEV5Gb28eDyXOwUHdGkYI9W3L5+GFRbeN6v7sAM/p0REREREzkME9Cs3QVTbWQDG891UQgKQlSWyYAExQe748UBqqrrtIiKSjBsnrjmBt+sK7qcPkn2PynIo63bnxZtnCefFY1YmFPWxbZaXhpWmpTgkkS8gGkC21v6JQA8u6YSgxjKOWwv7zmX99OwonPtXMf4d8bxh2X2XfoDfq9Ptz9bPi1eWp8nbjWzTOvUWyerbN3sfNuDnlIiIiIhIdd4AkLc+ESWIRcIcFttxa9HRwJ49gK+vcdmiRcDMmZwsl4jUN2SIuP6h+aUqSD1VZ76U3RPBxf59ZXW7I+OxAsvxnHwSzNgMRGfeQMUaCwG7JhzUZgCIw1iLmQhikszmlvloa+w711f/UCdc3LYdV99IUiz/Rf5+9P6v4fD96zp43bFhsDIyHivKp8neZ2CLoTb+98iY2Elk4UemYUuw/DMxDd8mH8PKyKb20Xz8nBIREREROQcvnU7X0NwH5+bmYu7cuY5sj9s7efIkBg0apG4jystFdr68rIWfH5CTA4wYoU6b6uqAoiJRQ9vPT7HKKfrMxbDPnAvfDzs88IAYfExPd8ju2Pf28/LyQoXuhtrNcElB/p3Yd83kTn2nKS1Gt0ULcX/Ft4rlPwf1x+VV6/DTs6Oaued9WOG/G2MdEJx3p/5uK0H+ndDQ0Ox/m6gN8W+//dhnronvm/3YZ/Zjn9mPfWY/9pn9vJvehNxOcDBw+LAyeF9TI+rqb9igTptqaoCICCAtTZ3nJyLnYDKgR0TkaqQJc68vXoYGH41h+f0V38J/2q+aPWnu2U1rgMyWB/OJiIiIiMi1MaDvqfz8gPx8UVtfbsECkSmvFk6GSUQ8DhCRi2vw0eDa4uVmtfUBYxmeBz/eZtc++8zZJ0rqEBERERGRR2NA35NpNMC6deZ19dWYkFKq4V9e3vbPTUTOIyCAAX0ichv3evXGxW3bcXHbdvwc1N+w3PvmDXRbtBD+036FDtrdKraQiIiIiIhcDQP6BERFAadPq1c/HzAG8hnQJ6KqKgb1icit/DvieZz7VzGuvpGkKMPzwBefw+/V6Xgs8FH4vTodD/39w2aV4yEiIiIiIs/htXv37ob6+no0NDSgvr7e4sXauoaGBoSFhan9GsgNPJqaiq6bNwMAKnJzcScwUOUWEZEaesfH48EDB3Dxrbdw7eWX1W6OR3riiSfUbgKRWwsGkA6gsTSKDQAWtE1zyA4nTpxQuwlERERERGg3bNiwZj84NzeXsxDbiTM3W3HhguFm0JUrwAsvGO6zz+zHPnMufD/sMHw4cOAAuh8/ju7JyS3eHfvefidOnGCfNRM/b83nkX2XnQ18/DGwc6fZqvkA5i9bBqSktMpTe2R/txD7zHXwvbIf+8w18X2zH/vMfuwz+7HP7Mc+sx9L7pBzkE/Ee/Cgeu0gInWNGSOu1Zycm4ioLURHAzk5wE8/ieu4OOWcRqtWAUlJ6rWPiIiIiIicEgP6pL6iIuOkuABQUKBeW4hIXeHhYsLumhpxISJydxoNMHkykJ4OXLwo5jaSJCczqE9ERERERAoM6JP6Vq8W1+Hh4rqqioE8Ik+l0SiPBUREnkSjEdn6DOoTEREREZEVDOiTusrKjLVjx4wBhgwRt1lug8hzSceBujp120FEpAYpqC8dCwEG9YmIiIiIyIABfVLXokXG29HRxszcsjJ12kNE6nvqKXHNM3WIyFNpNEB+vnlQX/67iYiIiIiIPBID+qSeVauM9fInTwaCg40TYn71lXrtIiJ1+fmJa2boE5En8/U1D+qnpgIxMTw+EhERERF5MG8AyFviD39/2WXiJlSq3TJyb6tWAcuXG+8nJorrESPENUvuEHmugABxzQx9ai11dWJAWX7h542ckRTUl34fAUB2NhARAdTWqtcuIiIiIiJSjXfeEn/EZsYiU6eDTqeDTpeJ2JJEhDGoT60lIkIZzJ8/35h95ucnLjU1DK4QebojR8TxgiW4qKWKioCZM4GRIwEvL+CBB8RnS37p3l2sY0kTcjZSUF8+UW5RETB0KFBerl67iIiIiIhIFd7flQOIjUKkYVEkFiSHAiVnGNAnx6uqMpbZAUQgf9065TbM0ifybFLJHa1WHC+Yhdqm2l25AoweLQZb3eE4rNWKQH5Ghm2vJzUV2LCh9dtFZA+NBtizR3wvJVVV4rMt/11FRERERERuz7tvMIDy72TB+0rszy0xCfITtYKoKJFxptEol0sTYjIrl8gzSccE1ohWhdedO8DnnwMbNwKrV7dsZzU1ls+ysLbc0WprRWa+JSNGiInYpYuvr3HdggUMkpJzWr9emQhRWyu+SxyEIiIiIiLyGN6Ra/QldvwnYlNlHpb4hyGxJBaZaxjOp1Y0f77INJMHUCRS+Z1du9q2TUTkPOSTQJJ6WhrUlmrVm55lYW25oy1fbizf5ucngqGnTwMNDcDhw2JQWbpcvCgC+0TOLiEByMlRJkQsWCAuHAglIiIiInJ73kAk1ugyEYsSJIbFIhNAbOYaZudT63rmGevrpJI7ZWWso0/kqeLjRXB18mQG99VUW+u6NbrLyoxZy76+wLFjYjA5ONjy9hoNkJ5ufT2RM5k8WQxKSZOIA+LzHhHB305ERERERG7Ou3LTRPj7xwKZYlLcwuRQZMb6w39JntptI3cUECAyI+PirG/j52f8B3XnzrZpFxE5l7g4kTWdk2P5TB5qfaNGieuWZOmrGViUl9pZt844N0NjAgKMGfzM1idnN2SICOpLiRCAmCdiwAAxZwQREREREbkl7/jEEoQmF0KqsBM45zPoMmOBzFgwpk+qiYoS1x9/rG47iIg8lTSfSUuOw2qV/ygrM9bnHzGi8UFkIlfm5ycGP+WT5UpzR0yZwknFiYiIiIjckHcJgOC+gcqlgf0QqkpziPTGjRPXBQVod+WKum0hIvIghmNuUJC4LihwfKZ9awf6pWC+RiPq5hO5M+lzvn69sq7+zp0iW1+rVa9tRERERETkcN6xADJTN6FStjBvfSJKEIsoFtIntURFGf4pfSiPp4oQEdksO1vU0ZaC2nbyvntX3Bg40BgcdHT5jtauy19VJa7nz+ccDOQ55s8Xc0XIS/DU1ADjx4uMfWbrExERERG5Be81ukzEliQizN8f/vpLbGYsMnWcGJdUpNGICd8AdCwsVLkxREQuoqhIBO4KCloevGvfHoiOFrd37Wp52+T27nXs/qyZN69tnofIWQQHi7r6iYnK5RkZzNYnIiIiInIT3kAk1ujEhLjGC4P55AQmTQIAPPDVVyo3hIjIRcTEOLaczSuviOuiImPWe3OYluxp7QnPpQGI4ODWfR4iZ5WUJAL78u+ALFv/vlu31GsbERERERG1iLfaDSCyavJkQKMR9ZwdXb+ZiMjdlJW1LOhuSXg44Osrbmdn2/94Pz9xLT+Gy2vyt0bAPTu72eWGiNzKiBGiBM+yZcrlGRkImjDBvbL1a2pEqbGRIwEvL3EZOtTx5cKIiIiIiJwAA/rkvDQaEUwCWr/eMhGRq2uN46Ss/FmzyuRINfjPnjUu+/hjcR0cbAz4O0pdHbBokfK5iTyZRgOkpJhl67e7ckVk68fEOH4gUA11dWKwsKjIuKysTJQg27BBvXYREREREbUCBvTJuUmTGbrDP5tERK1JKrUjnxDTEaSyO/LMeltJQXV5iR0pK1jaryNlZBjbOH++4/dP5KqsZetnZwOBgSLwLQ+Gu5PkZJ7pSURERERuhQF9cm7PPCOuDx5Utx1ERK1FKhUxc2bLgk5S5rujA/otKbsjZeBXVYlLTY1xgFaacNeRpD7w8wOWLnX8/olcmSxb/05goHJdRoYoVzN0aOvPcdEaAgKAhgbj5fRp47Gwpoald4iIiIjIrXjt3r27ob6+Hg0NDaivr7d4sbauoaEBYWFhar8GcmM+lZUImjABdwIDUZGbq3ZziMgFtLtyBT3/8AfFsp+eegrXXnoJP/fooVKrrLu/uhr9x40DAFSvXIlaqcSNHbp88gm6v/02AODywoV45IMPUJWejtvDh9u9rw7FxQiYOVPx+B4rVsB3507c69oV3+7diwYfH5v313faNGjKy3HxrbdwKywM/ceNa5VjutedOxgYEgIAqFm6FFdnzHDo/oncidedO+jyySfoumWLKL9jonbyZOjefNOu77qz8bpzB/3HjUO7K1f4O5KIiIiI3Eq7YcOGNfvBubm5GDRokAOb4/5OnjzJPrNH374ARGB/0H33tc4Eim6InzPnwvejjVVVAcXFikUdiovRdfNmIC5OZKg6unZ7S3ToYLjZ48oV9LD3s5KRAeiD+QDwSPv2AICA8HCRtWqnKn3fBWg0gNSW3/wG2LkT7a5cwcDPPgOSkmzfYVQUUF6O7v/6F7rPnAkA8Pnv/3b8d0LK/Ndo4JeUBD8Vaujzu9587Lu2dfLkSfitWiVK8GRnA6tXK8ob+u7cCd+6OmDPHhVb6QB/+QsQEyN+R3bo0KxjooSfUdfB98p+7DPXxPfNfuwz+7HP7Mc+sx/7zH4suUPOTaNBnRTE37jR9sfV1Yl/UGNiRCmLsrLWaR8RuZaMDGDAAOc6Jvj5GetaFxTY99iMDFGqRxIXB3Tq1KLm3OvaVdyQavIDIigvDYIkJ9vXzkmTxHVBAXDzprjdgqCaVVK5ouhoTohLZCtfXzHfRGUlkJNjnLsIEPNdyI8vrig62njssvf4SkRERETkpBjQJ6dnKBlhrf5pVRWwYIEI3EdEAN27Aw88IIL52dniH7ja2rZrMBE5hz17UJWeDiQmKjPya2uB8eOVAeu2JtXNLysTwWep3ntZme3Hq7IyZbBtyBBg3Trj/WYGzev1Gf4K8jYC4vhqa73/ESOMAXZpQtzWCOhL76c090prKyvjgDG5l8mTxcS5cXHGZaaDhq5IKmP21VfqtoOIiIiIyEEY0CendysyUtyorQXKy5Uri4rEJG4bNojAfUFByyaVJCL3odGIAcGkJJF9um6dMbCs9iSJdXXKwUZfX2NJMVvbJU0AC4hgfn6+cfJaRzA9ls6fb2xjTQ0wZYptgyIajTGgduCA49qntkWLOGBM7ik93Tyov2CBeu1pqVdeEdf8rhIRERGRm2BAn5ze7eHDjaeAS5mQZWXin8uRI60H8H19RRApK0tkiBKR59JogIQE4PBhY1BfHhBXi/z4JR2nVq+2LVAuZbu3RjAfMG+DRiNKckj9V1QkBlNtIZXdOXHCce2z5ptvWv85pGA+kbtKTzcOxAHiu27P3BnORDq2yuYIICIiIiJyZQzok2uQgkGvvQb06AEMHWoeSEpMFEGt69eBhgZxnZPDespEZDRkiJgUFxABaTXL7gDK5x83TlzX1Ig69Y2prTUOcKanOzSYb6ih/8MP5iuDg8XzSWwdfIiKEtfSAIajBx+AtquTvXMnkJpq/rxE7iYry/jdBcRxafly9drTXBpN65T5IiIiIiJSCQP65PQ6FBcDhw6JO9euATqdcgM/P2DPHpE5Fh7eOoEiInIf8+eLAE9dnQjqq0meoT95sjE4vGqVMQPfEiloHRCgnMRSrpnlJRp8fBp/fHS0cRLfmhoxV0lTfH2Bvn2B+npxXyrd40hSwK6srPVKr9XVKQdbEhJa57UQOQPprBx5UH/VKjEHiauVN2RAn4iIiIjciDcA5C3xh7+/8TJxU6Xa7SJPp9WK+syBgQiYORPIyzPfRsq0PX1a+c8mEVFjNBrjMUPtsikHDxpvm048O2WK9QEH6XHh4ebrpDOSTOccsUdAQOMBO/lEw/LX0Ji+fcX1/feLgOD48WIgtiXtlNNojIMbtgwyNMeGDcYzI8LDlZMQE7kjKagvP9ZotUBgoPj+si49EREREVGb885b4o/YzFhk6nTQ6XTQZcaiJDGMQX1Sz4IFItCzc6d5vVM/PxHEr6wEjh0TWaLMyCcie40ZI65tDUY7mpQtajqp6vz5xnrPdXUiqG+p7vPOneJaeh1yUqBdCjw3h0ZjPaBfVSUC5o88Iu7bOigyYIC4/vln8RitVmS7DxggXmdL2iuRgo7Jya1TL3v1anGt0YhyJESewFJQXzpbJTCw8bOJnIWrnVFARERERNQI79RMIDR5ASKlJZFrkBkLlOTuB0P61Gays4GZM4GICMuTLEp1mysrRRCfp04TUUtIgamCAvUCPb6+IiiWkWFcJgWKpaB8TQ0QE6OsU19UZAxWN5ah35LJYQMCROa8/Hm1WqB7dxHAmzkT+PprsbyqyrY+bGxy8p07xdwo8tr0zSENcNTWOr4sSFGRcX9Ll7J2PnkWX18xT1FKinJeIum7NnOmc2frc0JcIiIiInIj3iUAgvsGKhYG9gsFSs4woE9tY+ZMEbDKyFBmegYHA1lZKD98WJTViYvj5LZE5BhDhhjP7mmt8ixNkcr+mE4sGxAg5gWRjndFRcpA965d4jo42PLgplTTvSUZ71KwWiqHU1srzp6yFiC3pQ8nTza+psmTLQ/OLlrUsiB8VJTxfS0vFwMQERHGMxqaq7zcWDvfz884hwCRp1m2TCRXJCQof5NlZAAjR6o/L4klZWXiGMvfkERERETkJrwaGhoa1G4EebCaGhFwMRUVJU7v5j9fRGSvqiqRRZ6fbzmDXRITIwLRfn4iQNXWx5vsbNEGQNRiT0hQrt+5U5SiAUTbTp8WAfABA0SAOTFR1LA2VVcHPPCAuH3xYvMyyZOSRAA7K0tMgjt+vLKsRnCwyLi/ehXIzbW9D2fOFIE/jUZs7+cnzspKTjYG8sPDgd/8RgziNodWK9prKj3d/n1mZADLlysHGaz1O5GnKSsTxzD5PBgajcjiNz2eqWnVKvE9nj8fWL9eLKutVQ56ygd5iYiIiIicnLfaDSAPJ89KHTFCZKXm54sgEoP5RNSaJk0S1zU16mTpT55sDLanpVleLwXF6upEhjxgLB0xebLl/Wo0xiz95r4u6fFVVeIiBfM1GjFIcPq0CJAvXCiW19QoSwdZ85vfiOu6OmN5tfnzRXBfmtC2oEAE/gcMaF5t7qgo0TbTvyHSYIKtioosn5Vgrd+JPM2QIWI+o/nzjcvq6sSZNmpPOA6IoH12NvDRR+J+djbg5SUunTuLs3ekS+fOxnXSmT1JSSzVQ0REREROiQF9cg5RUcDhw+I6PJxZUkTU+uQB9Y0b2/75NRpRix1QBs3lUlKMwXWtVgSl6+pEpr4UALdEqlcvBbLsJZXC+eor5fL165UZ/+Hhxvu2PFd4uLHde/cal2s0IvNdrrxcZNrHxNhfhicuDvjpJzFALPUfIPpv/HgR2LcUqJMCgNKcLqalkFJSGu93Ik+j0Yjjwp49zvPbTTpzoHNn5RkEttb4r6kRAxLSpL8LFjj3/ABERERE5HFYcoeIiNyLrSV3AFGbftEicfv69bYPSNXVibbW1IgBhpwc820slZCRl46wRP6Yw4cbn5DWktpaEQwbMUKcMRUYKErvZGWZbyvvQ1tK/MhLCcm3r6sT7U5LM8/ulQL+pnW7m1JTA7z0EvD994BOZ75eozH2TVmZ5aBdQIDIQnaWYCWRs6qpEd/toiLbjr+OVlsrgvC2TK7t56cc7ANE4N/a4KGfnzjzR5r7hIiIiIhIRQzoExGR56qtFeUV6urUCUABorbzqlXKuvKmpHr/Eks19+XkAwVNBf+t6dzZWGKnMXV1og9ra0WWri0Br+7dRdukGv2mtFoxSCCvzQ2IANz69ba/T9LgzogRop32ThTs6ys+F8zKJ3JupnNxmJo8GYiPt+3YUVAgziDasMF8kC8qShyDLE1ITkRERETURlhyh4iIPJevrzGgbG9ZF0eJjxfXUoa6Jenpyiz7prLFNRrj62pJHf2amqZLTWg0xrrypgF4a6Sgv7U+j4oSWfGJicqM/PJyUQpn/Hj7gvNFRaJvs7JEOZ7GAvQBAaLv0tOVtf2JyPkUFQFDh1qe70IinWlk60BgeLgor3XxIrBsmXKdVisGCUeOFAOxth7ziIiIiIgciAF9IiLybNLkuPJ66W3Jz88Y4JbXlZfTaEQ5HnvKzcybJ65ra5s3saN8YtymSH148KBt+5a2b2ywQKMRk1JWVppPRKvViiDelCmNT77p52fss9OnjYH6Y8eAhgaxLD9fXA4fFssqK42Bf5bZIXJeNTUisG5tcE+jEQH5PXvsO3bKH5+SIo4NpuV5iorE2VUDBojAPhHR/9/eHQK1zYdxHH/eu/dumSsujrjhYGp1dGpFUVyn+qLoFEMN1JhiVe0URVFH3YqCKYoriqKo7FxRq1scr3jufwkM2rRNmq75fu52WVlJM0S4+/2f/P4AAEwRgT4AINnMBHZcE/oiIoWCHp+b0BfRcNrU7ASpe1ha8qb6xwn0Fxf1GGQC1YRdzWawhRFzXXd3w99r27qYcXb25/+70dCJ/YUFPW5u6iLA+bkuFvifHnjuujMZ/TPqPgMA4vXcvcaydEHu9lYD+UkX5tJp71xPVaLt7ekTAnEtCgMAACBxCPQBABCJN4zJ5TSE6vcHV8kcHOgUedDqiHfv9DjOYoUJ6a+uhr/Xcbzrr1aHv9+/EW5Q2ayGauXyn6Fav6+LCbWa9mivrWnIv7Ehsrwc/DMA/J2yWa3ourjQqpzj4/B77nd39QmeszNdXPXfh6pVXVQcVlEGAAAAhIBAHwCQbLOwuaFleRPigypkRjXJ0wfm5xJkQt9//aVSsKDetkd/csCyNEi7vQ22OW6jodOzAOaP4+gC5/29huz7+3pPiLIqy7J08aBc1vuQfxPwVks38wYAAAAiRqAPAEi2OKt2/FZX9Ri0hz4IE+j//Dn695oJ/VYr2PtNL36vp0H6MJY1/oaSqZRIsajTuL9/6/HsTCd083m67wFEL5XSOrBi0ftavc6UPgAAACJHoA8ASLZBFTfTZLrew5zQNxtB1uujVwqlUhrq9/vBFj2KRe/z9vaGf57j6Hnfvh28d8AwlqVTudmsTuienIj8+qX1RONshAkAQVmWPi10eKivXXey+xkAAAAQAIE+ACDZjo70GHf1zsqKhuj9/viT64+ZjuegU/OPmSn9INU4/tqdbnf4ZL+Zom82o3lKYndXp/dNJUfQfQcAYFTFonePGWcTcgAAAGAEBPoAgOSq1bygexZqWkwgFLTmJgizUBFkav6xN2/0GPT7traCn5vNagHMk0JBj3FusA4AAIBEINAHACRTpSKyuem9Nn3zcTIh981NeOfc3tZjt6sLGKMwE/pB5fPBf45MzAOYJ6Y2DQAAAIgYgT4AIFlcV+TDB5GdHe9ruVz8lTsi0VQ25PNel/yPH3o03fXD9g8Y56mF6+tgFTfp9Gz8zAEgDLOywToAAADmHoE+ACA5Oh0NsqtV72srKyLHx/Fdk5+Zbu92g4fuw9i2bhAr4p3LdbW7vt8f/L1RBu6WJVIuR3d+AJimMKvSAAAAgAEI9AEA8+/8XOt1Xr9+GLqk0yIXF7PRny+i1+E4Guib0D2MDXKLRT23WSgY5Xo+f44u2M/ldJr/v/+iOT8ATMu3b3qcld8nAAAAmFsE+gCA+dPv6xT+xobIy5cia2vaH+/frDCfn60w31ha0us30/Rh1O9Yli5eiIjU68G/L5US2d+nGgcABqnVvHv2qHuPAAAAACMi0AcAzJe9PZGFBe3JbzQehvgiGlIfH4ucnHjd8mHodvUzJ63JMeH55aUer64mvzYRr86nVPrzZwIAGE+7rfd+kYeLpwAAAEBE/o37AgAACE2lIvL169P/ls2KrK/rZP64U/n+yfl2W19fXmqY75+kH9ZNP8irV3o0Pf9hVO6IiCwv67HXEzk6CuecAJBk7bYu4ppFUlNvBgAAAESIQB8AMD9KJe/vlqXh/fq6hvmDpvFbLe2rv7nxOuZdN55NDs0kvQmIOh1dIJg0JMrldIPcXm+02h0AmFW9nsj797rBtrl3Tsv5uX62WcC1bZFPn6Z7DQAAAEgkAn0AwHxot70wPp8XOTwcHILX6yKnpxrKTDJR7+c4IoXCZMFSOu0F70anM3mNg2Vp2LSz4517lA1yAWDWmM3Dw7qHB1WtejU7Inp/PTnRezcAAAAQMQJ9AMB8MFU4jqMd+U9N5LuuBvlfvoy32ezKirdIYNtaj2Pbugmi/98mYVki29u6F4D/usOQz+t5zfnC2HAXAJJkf19/hxiplIb5mUx81wQAAIBEIdAHAMyXQkFD8VZLQxd/GG5675+SyYisrnoT8tOub/D7+FF77sMO3G1b64caDX1dKunrOP+vADCp09PwFlWf0+vpE07+yjLHEfn+nXsoAAAApopAHwAwXzIZkVpNZHNz+HvTaZGtLe2Xn6WNDE19g3+zxbAcHGjNkOvq4sa0qyoAIGyViv5Jp/V3wIsX3tNT4+h0vEqyuzt93Ww+fM/KisjFxWz97gAAAEAiEOgDAObL6an2Gw+Sz2uQP8sVCem0dt77qx3CsLQUzXkBIG6t1nQ2M89mdTJ/0GbrAAAAQET+ub+/v4/7IgAAmFizqRPtfrYtUi4/3Kgw6lqGv4Hrapd+paITprO8sAEAz3Fd3Zy20ZjO00aplO5xsrtLmA8AAIDYEOgDAObD40DfcUSurwnvASAJWi3dd6TT8b52eTn6eRxHZHHRe51K6UKwZemTUwAAAEDM/gfnH1sVXpZ9awAAAABJRU5ErkJggg==[/img]

Ссылка

Елена Маркович

18.01.2024 10:58:16

	Цена, р.с НДС/кг
Наименование продукции	тип 1	тип 2	тип 3	тип 4	тип 5
Яблоки	61	58	57	55	54,29
Груши	85	81	79	77	75,65
Свекла	40	38	37	36	35,6
Апельсины	52	49	48	47	46,28
Салат	200	190	186	180	178
Виноград	180	171	167	162	160,2
Морковь	45	43	42	41	40,05
Огурцы	85	81	79	77	75,65
Помидоры	90	86	84	81	80,1
Бананы	49	47	46	44	43,61
Картофель	35	33	33	32	31,15
Укроп	250	238	233	225	222,5
Персики	300	285	279	270	267
Баклажаны	210	200	195	189	186,9
Петрушка	250	238	233	225	222,5
Мандарины	68	65	63	61	60,52
Базелик	400	380	372	360	356

У меня вот такая таблица, и тут условия как в столбцах так и в строке, Почему то выше приведенные формулы не работает. Помогите, пожалуйста.

Ссылка