Самая длинная победная серия
Предположим, что у нас есть расписание работы сотрудников, где указано количество рабочих часов в каждый день недели, либо ноль - если человек не работал. Задача - определить сколько максимально дней подряд каждый из коллег выходил на работу:
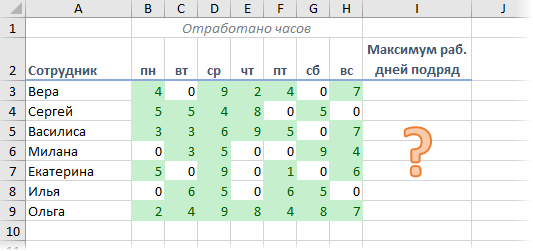
Другими словами, определить максимальное количество идущих подряд значений, удовлетворяющих заданному условию. Иногда такую задачу еще называют нахождением "самой длинной победной серии", приводя в пример непрерывную цепочку последовательных побед в спортивных соревнованиях. В английском языке есть даже специальный термин - "winning streak" для такого случая.
Для решения нам потребуется функция ЧАСТОТА (FREQUENCY), о которой я уже писал. В нормальном варианте, эта функция нужна, чтобы подсчитать количество чисел из диапазона данных, попадающих в заднные интервалы (карманы):
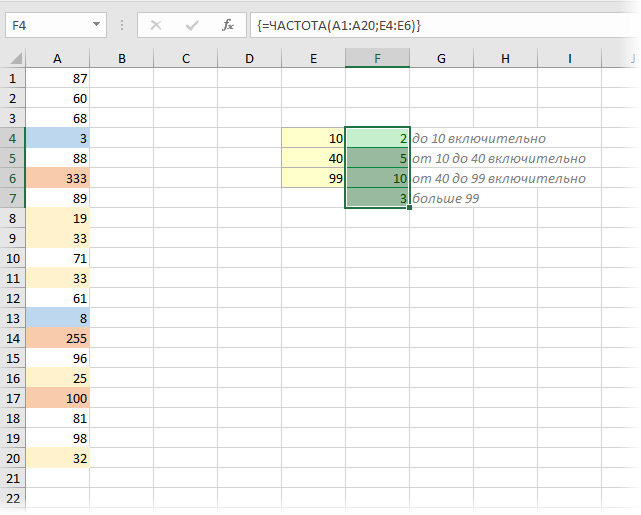
Необходимо помнить, что эта функция должна вводиться особым образом:
- сначала мы выделяем диапазон пустых ячеек для результатов (зеленые в примере выше) - на одну больше, чем границ интервалов (желтые)
- затем вводим нашу функцию, указывая два ее аргумента - диапазон данных (A1:A20) и диапазон интервалов (E4:E6)
- и жмем сочетание Ctrl+Shift+Enter, чтобы ввести функцию как формулу массива
Давайте немного изменим формулировку предыдущего примера для наглядности:
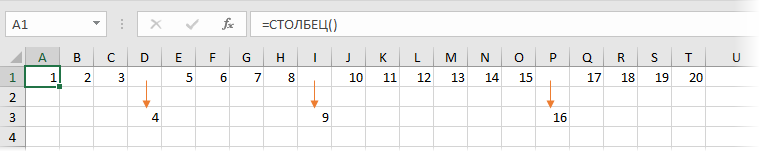
Что изменилось:
- Диапазон исходных данных расположен по горизонтали, а не по вертикали.
- Теперь это не случайным образом перемешанные числа, а возрастающая последовательность 1,2,3... полученная с помощью функции СТОЛБЕЦ (COLUMN), выдающей номер столбца для текущей ячейки.
- Допустим, для примера, что числа 4,9,16 - это границы интересующих нас диапазонов. Я "выдернул" их из исходной последовательности в отдельный ряд.
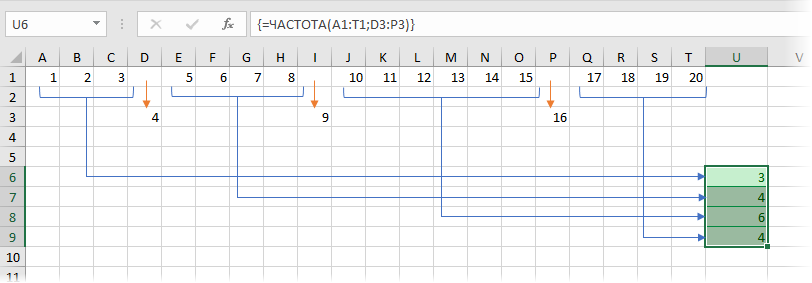
Ничего не напоминает? Например, первую строку нашего табеля рабочего времени? Только вместо часов работы у нас последовательность чисел - номеров столбцов, а вместо нулей границы интервалов. Так что теперь можно и нашу задачу решить изящно и компактно:
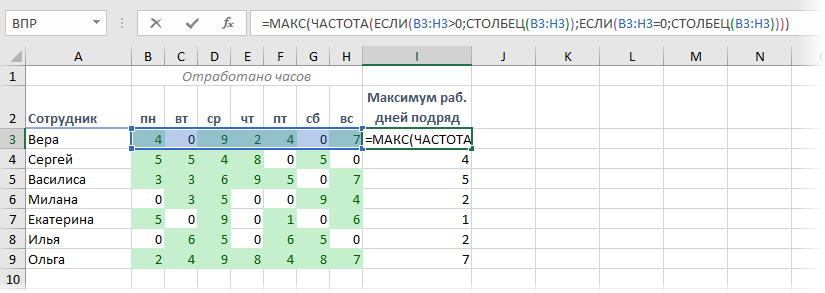
В английском варианте это будет =MAX(FREQUENCY(IF(B3:H3>0;COLUMN(B3:H3));IF(B3:H3=0;COLUMN(B3:H3))))
Разберем эту формулу по кусочкам:
- ЕСЛИ(B3:H3>0;СТОЛБЕЦ(B3:H3)) - проверяет, чтобы ячейка была >0 и выводит номер её столбца. Для первого сотрудника на выходе получим массив {2;ЛОЖЬ;4;5;6;ЛОЖЬ;8}, который потом используем как диапазон исходных данных для функции ЧАСТОТА.
- ЕСЛИ(B3:H3=0;СТОЛБЕЦ(B3:H3)) - то же самое, но наборот - выводим номера столбцов для нерабочих дней. На выходе получим массив {ЛОЖЬ;3;ЛОЖЬ;ЛОЖЬ;ЛОЖЬ;7;ЛОЖЬ}, который потом подставим в функцию ЧАСТОТА как диапазон интервалов.
- И поскольку нам нужна самая длинная последовательность, то функцию ЧАСТОТА мы вкладываем внутрь функции МАКС.
И не забудьте после ввода формулы нажать сочетание Ctrl+Shift+Enter, чтобы ввести ее как формулу массива, конечно же.
Как легко сообразить, подобный подход можно применить и в любых других похожих задачах поиска максимально длинных последовательностей - достаточно просто подкорректировать условия и антиусловия в функциях ЕСЛИ.Вот и все. Не так уж и сложно, не правда ли? ;)
Ссылки по теме
- Что такое формулы массива, какие они бывают и как их вводить
- Что такое функция ЧАСТОТА и для чего она используется
- Поиск и подсчет самых частых значений функцией МОДА и сводными таблицами с группировкой

Подскажите пожалуйста, а как применять данную функцию если данные будут сформированы в столбцы и будут браться из умной таблицы? ведь простой заменой диапазона на =Таблица1[#Данные] не обойдется?
и в продолжение вашей темы: как подсчитать сумму отработанных часов в самой продолжительной серии? ведь в теории может быть 2 наибольших одинаковых по величине интервала и разница между ними как раз может быть в количестве часов.
А можете дать наводку как посчитать длинную победную серию по условию, например для конкретного работника?
Формулу я уже адаптировал для подсчета по строкам, а вот условие что для конкретного работника - никак не могу "запилить".
Спасибо!
Премного благодарен! Как раз мой случай!
Есть диапазон, в нем отмечается "промах" - 0, и "попадание" - 1.
Всё отлично, я изменил формулу и получился подсчет промахов.
Но пустые ячейки в диапазоне так же считаются за "0".
Пробовал вставить и СЧЁТ и СЧЁТЕСЛИ... но видимо вставляю их куда-то не в то место или они здесь не применимы.
Факт - не получается исключить из диапазона пустые ячейки.
Как реализовать, что бы подсчитывать только самую длинную серию "0", но исключить пустые ячейки.
Пока я могу только заполнять наоборот. А это не совсем то, что надо, ибо потом я считаю "1" в других формулах.
{=МАКС(ЧАСТОТА(
ЕСЛИ(
СЧЁТ(A1:BH1);
ЕСЛИ(
A1:BH1=0;
СТОЛБЕЦ(A1:BH1)
));
ЕСЛИ(
СЧЁТ(A1:BH1);
ЕСЛИ(
A1:BH1=1;
СТОЛБЕЦ(A1:BH1)
))
))
}
{=МАКС(ЧАСТОТА(
ЕСЛИ(
СЧЁТ(A1:BH1);
ЕСЛИ(
A1:BH1<>"";
ЕСЛИ(
A1:BH1=0;
СТОЛБЕЦ(A1:BH1)
)));
ЕСЛИ(
СЧЁТ(A1:BH1);
ЕСЛИ(
A1:BH1<>"";
ЕСЛИ(
A1:BH1=1;
СТОЛБЕЦ(A1:BH1)
)))
))
}
Осталось два вопроса :
1) как можно получить позицию начала и конца самой длинной неразрывной последовательности
2) можно ли сделать игнорирование случайных разрывов - то есть тех, которые по длине меньше чем оба разорванных куска
что то типа такого 00001001002202222200222220222010110100, где 2 искомая последовательность, а 1 левые флуктуации
ну и аналогичная задача для нее из пункта 1