Поиск последней непустой ячейки в строке или столбце функцией ПРОСМОТР
На практике часто возникает необходимость быстро найти значение последней (крайней) непустой ячейки в строке или столбце таблицы. Предположим, для примера, что у нас есть вот такая таблица с данными продаж по нескольким филиалам:
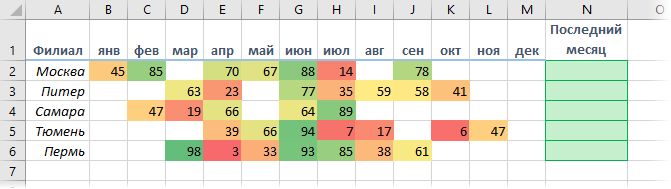
Задача: найти значение продаж в последнем месяце по каждому филиалу, т.е. для Москвы это будет 78, для Питера - 41 и т.д.
Если бы в нашей таблице не было пустых ячеек, то путь к решению был бы очевиден - можно было бы посчитать количество заполненных ячеек в каждой строке и брать потом ячейку с этим номером. Но филиалы работают неравномерно: Москва простаивала в марте и августе, филиал в Тюмени открылся только с апреля и т.д., поэтому такой способ не подойдет.
Универсальным решением будет использование функции ПРОСМОТР (LOOKUP):
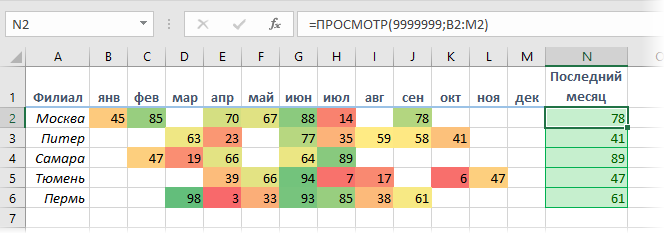
У этой функции хитрая логика:
- Она по очереди (слева-направо) перебирает непустые ячейки в диапазоне (B2:M2) и сравнивает каждую из них с искомым значением (9999999).
- Если значение очередной проверяемой ячейки совпало с искомым, то функция останавливает просмотр и выводит содержимое ячейки.
- Если точного совпадения нет и очередное значение меньше искомого, то функция переходит к следующей ячейке в строке.
Легко сообразить, что если в качестве искомого значения задать достаточно большое число, то функция пройдет по всей строке и, в итоге, выдаст содержимое последней проверенной ячейки. Для компактности, можно указать искомое число в экспоненциальном формате, например 1E+11 (1*1011 или сто миллиардов).
Если в таблице не числа, а текст, то идея остается той же, но "очень большое число" нужно заменить на "очень большой текст":
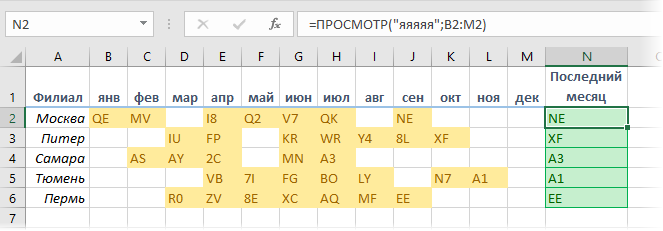
Применительно к тексту, понятие "большой" означает код символа. В любом шрифте символы идут в следующем порядке возрастания кодов:
- латиница прописные (A-Z)
- латиница строчные (a-z)
- кириллица прописные (А-Я)
-
кириллица строчные (а-я)
Поэтому строчная "я" оказывается буквой с наибольшим кодом и слово из нескольких подряд "яяяяя" будет, условно, "очень большим словом" - заведомо "большим", чем любое текстовое значение из нашей таблицы.
Вот так. Не совсем очевидное, но красивое и компактное решение. Для поиска последней непустой ячейки в столбцах работает тоже "на ура".

Сразу возникаем мысль, а как найти значение первой непустой ячейки через ПРОСМОТР?
...Логично нужно перевернуть массив, например, так:
Для чисел:
=ПРОСМОТР("яяяяя";ИНДЕКС(B2:M2;Ч(ИНДЕКС(ЧИСЛСТОЛБ(B2:M2)+1-СТОЛБЕЦ(B2:M2);))))Для проверки можете убедиться, что диапазон считается вектором: напишите формулу =1/(B2:M2<>0) и нажмите Ctrl-Shift-Enter, а затем растяните формулу вниз.
до этого я в макросе перебором делала - а так намного проще и удобней!!!
а не подскажете как ее интерпретировать если значения меньше 1 (дробное) - на досуге, когда у Вас время будет....
спасибо еще раз! уличная магия какая-то но работает круто!!
Если не получится применить, задайте вопрос на форуме, приложив пример
А более универсальной формулы нет для которой бы было все равно текст или цифра.
Иными словами искать последнюю заполненную ячейку в строке?
=INDEX($B$1:$M$1, 1, MATCH(9E+307, B2:M2, 1))
=ИНДЕКС($B$1:$M$1; 1; ПОИСКПОЗ(9E+307; B2:M2; 1))
Как работает:
В функции ПОИСКПОЗ мы ищем число в диапозоне B2:M2 которое больше (т.е. последний параметер функции = 1), чем оооочень большое число 9Е+307 (самое большое число, которое поддерживает эксель)
Такого числа, понятное дело, нет, поэтому поиск останавливается на самом последнем числе диапазона перед пустыми ячейками.
Если же между заполненными ячейками нет пустых значений, то можно использовать функцию СЧЁТЗ() :
=ИНДЕКС($B$1:$M$1; 1; СЧЁТЗ(B2:M2))
(в примере в статье этот метод не сработает)
Напр:
78
98
0
65
32
0
0
0
надо чтоб ответ был 32
Работает ли этот метод для дат в столбце. Вроде всё ввожу правильно, а значение всё равно некорректное
А как в отдельную ячейку вывести список месяцев в котором, в котором были сделаны записи?
Например, для первой задачи в каких месяцах отмечалась активность Самарского филиала.
Подскажите а как сделать чтобы в результате поиска определялось не последнее значение в ячейке, а последний месяц в котором имеется это значение? т.е. для второй строки результатом поиска должно выдавать "сентябрь" а не "78"
Как найти последнее значение в строке отличного от значения равного 0, значение высчитывается формулой.
Меня тоже очень волнует этот вопрос "как вывести последнюю заполненную ячейку, если надо просматривать через одну (либо выборочно поставить какие нужно просматривать)".
Подскажите пожалуйста, есть ли решение ?
[IMG]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABzwAAAMICAYAAAC9xJPXAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAP+lSURBVHhe7P1lmGRHniZ61sd9dj/cnbtzZxqm6TbU7Ny90z1d3aqSlBTMzMzMkMHMzMzM4MERCYKCLmZmLpWYpRJUvWv/4+6R7pGewgT31Kvn+Skz3c3h2LFjB143Ox975OoxbodHr53g2skhdrbWsbWxiqvHB3js+hWLZY3kNccHu9jf3db+bqnMrUj5k8M97O9saZ/1fl9PRNbH2I/Idn2stm9LZT6I075GvS/7CqL70/UrR9o2fqS2dUvPExERERER0TuT86qD3W0c7e9YfJ7uH3u6TV5TJ6L7zscef+QqbqfPPv4IPvfpR/GZx65ZfN7M9Suq3HXtNY8/cuXm59+F8bWffvQ9fBYR2QTZnmW7lu3b0vMfzIfra4jINtz+voOIiIiIiOijhedVHw1y/Z7X1InofvMx+cUOEREREREREREREREREZEt+pinpyeIiIiIiIiIiIiIiIiIiGzRx+ztHUBEREREREREREREREREZIs+5uHhASIiIiIiIiIiIiIiIiIiW/QxX19fEBERERERERERERERERHZoo8FBgaCiIiIiIiIiIiIiIiIiMgWfSw0NBRERERERERERERERERERLboY1FRUSAiIiIiIiIiIiIiIiIiskUfi4+PBxERERERERERERERERGRLfpYcnIyiIiIiIiIiIiIiIiIiIhsEQNPIiIiIiIiIiIiIiIiIrJZDDyJiIiIiIiIiIiIiIiIyGYx8CQiIiIiIiIiIiIiIiIim8XAk4iIiIiIiIiIiIiIiIhs1k2BZ0pKCtEdcbatWTtLy0B0L7BtEhERERERERERERHdmlngmZSUhLi4OERFRRHdNtHR0UhISDALbGxBYmIiYmJiLC4T0d0SGxur9c2mbVO2J7ZNIiIiIiIiIiIiIiK908AzNTVVC6acnZ0REBBAdFsEBgbC29sbnp6eWsJuGtpYs7S0NO37u7m5actwdrmI7gZpey4uLggLC9P6aGmb8qdxm2LbJCIiIiIiIiIiIiIKMA88w8PDERoait3dXezs7ECn0xF9KIeHhxgcHISrq6vNBZ4eHh4oKyvD8fGxxWUjutOOjo607cbf398s8JTtqb29XXve0uuIiIiIiIiIiIiIiD5Kbgo8ZSSRhFQHBwfY398n+lCuXLmCkZERmw08Kysrcf36dYvLRnSnXbt2TWuLlgLPrq4u7XlLryMiIiIiIiIiIiIi+iixGHjKE3t7e9pIT6IPQ0ZHDg8P22zgWVFRgatXr1pcNqI7TX4wIH2zpcCzs7NTe97S64iIiIiIiIiIiIiIPkoYeNIdxcCT7kfSP0o/KSPhxZ3qLxl4EhERERERERERERG9OwaedEcx8KT7jbF/XF9fx+LiItbW1rR7Ht+JPpOBJxERERERERERERHRu2PgSXcUA0+6n0jfKH8ODAwgPz8fmZmZyM7ORnt7O7a2tk6fv10YeBIRERERERERERERvTsGnnRH3anAMzExETExMZr4+HiLZT6MOxF4yjYl2xa3L3NSF7ZQH8bv2draCnd3d8TGxqK2thbe3t5wcXFBb2+v1t4tvfaDYuBJRERERERERERERPTuGHjSHXUnAk8JO2VUXXV1teby5cvaY5bKflB3IvCUEYAy/enGxsb7mgLVGLRZes7WyXJJXQhLz1uTo6MjrS1LwOnk5KQFjm1tbXBwcMC5c+dQX1/PwJM+uvYOcKi2kcN91V9Zep5sw94+Dg6PcHSgjgNPH5N1e2x4TO279g+5rumDM7SnQ7an90YdJ2nb5OHBe68f9Zp97TWH2N9Tx1eyXcs2/H7e425S38+0j9ndN+xPDm60CWM7OVDt5KbXExERERERERm878BzT52EHh2rk2h10mlGnUTv791cXuwbTly1ctprpSxPWD8K7kTgGRkZqb3nW2+9hbfffhvXr1/XHrNU9oO63YHn9vY2hoaGtFBMQrKpqSkt+JTnbrmtqceNgaCEpTqdzmI5WyXLtrm5idnZWe1emJbKWIuDgwNtfWVlZeGf//mftX5SvvfExASSkpK0/nN8fNziaz8Mqwo8tQuSxj78ZnJh8ubXqTYs/b9ceD0te6hd6La8DzBc2DV5X71j7U+5IG4sq+2L5DGLnyv2sH8grz3EgcV9k4y4PjS8/w2Ht9yXqWU5kPLq/W664Kr/rGNLn6UFSPoLzTfeV8of6svf6uKtxQvU+tcdqX717PcWx2rd6EOEG+WlPo+1fa7xMQPj+jyU/f2Z5wy0z1Lf4Vi+wy3K6KnvpVvD/MwkZpc3sb1juEj9Lm3mlNkymrzuDG3d3PJit7Q11bbOtB/9+rzVa4z0rzV9nbGdmvbP+uMfVR/yvFk9W7ZnCHa09SL1bKHM7q7aFrR6Nv1sw3o8U+fatiTvd6asGWkb2jLvYueW7UW1O4vfX7WXnU0sz09hamEVmzr98u9srmBhVq3bpXVs7x5At7aIuelpLKxuQid1d9P7EN2CoT3p+4oN1Z72sb22gFnVnhbX1HHOe25PqpxsX2f3Fxa2d2nDB4em25hh2zYp895IP/Ee92fSh5l+pvr7wdkyyt5NfZ1+n3D63aS+tjewJPW1sAbdLfd3JuRzdJtYXZjG9NwC1nQH2N1ex5Jswwsr2DT2z9ZClnFzVd/HLK5hS/qYdeljprCwYuhjVD1trcxjZmoWK5vqWPiW+wEiIiIiIiL6qHsfgaecIOuwpU5CZyYnManIxX6N+vv00go2dtWJu+lJqHqPvQN14rq1jvnpaUyMj6vyU5iZW8aGTi6m8oT1fncnAs+IiAiMjY3B+N/jjz+uPWap7Ad1OwNP2ZZWV1e1oLOqqgo1NTXaVKg9PT1a0Hd2tKf8XUjAKSNCZRuT5V1ZWTF7X1tlXD6pE7kXptz/clr1D6Z1YC3kO0l/KG1Avqunpyc+8YlPaG1ZAlC5oCnrZWlpSQtvb3cobVWB5/YaFmamMTVh0vefmsTM8gZ0O6rOTl8jF5nVutYtY2Fe7TMmVP8/LvuLOcyvrEO3p/YBpu+v7OxsYWVuClOTZ95f/XtqegaL61K/si/awfbGEmamZrSAzfQ9NHtyMXsHWyszmJqZw8qWvObG83tqnR4eynssYGbG+DnjmJyaxuKS+m67Bzgy2z/J63XYXJnH1NQcFte2b7RXaSPqe68tzmBiZgErm7I9G14nZbbXsTyn9pHzS1g3BEh7u9tYW5rD5PQ8ljd0Fi6WH2Bft6F/nVygPn3dFlYX59Q6MKkbE+Pjk5hbllBKlZXyO5tYmZ/B5Iz67C2T7yXrRreOhblpTM7L+0tbN/l8ofblW8vzmJV1sbCGbdlnny2jUZ8jZbvzEODljqT6KazuyCgc9dxpm7n5u+qptjSp1vecfAcZhSTLqNrB1qp2zGDW1tRxxty8OnbY3jM/zlC00EC1td3tJcypOps8fc0U5g31d6uAUl57cKg+c3MRs7OG16nPnZxaUOt5EztqOfYN639rXbU5Of5R7WRu5Z3Dhz31Ot22Wg6tfanyi6oOzdaz1NsBDg9Uu1qfU32gKqe2j3H1+VOqXS+tqHYtgY7hM2T9bK0tYXZiTCtz43uq+psyqafxMUzMLmJtaxcHe6q9qHZmWv/y2unpOSxLG1bbgbaejN/5UK23iTokBrggME/1y1tXcKL24Rv9JYjxegi+Oeqxncex2JiEIEd7xNcMY2nvGIcW2wXRzfYOVXvqK0KU50Pwz+vEzM5jmK+PR4CjIxLrRrGs2pPlH6iYUn3u4b7aLtewtDilzkeM7VvtD7TAbEfrq7TtXW1je/s7qt9UfbeUUduY9OFLa1vYtfCjglvT7892t5cx/477M/12faD66qU51cdLGfW5UwuLWNWZ9l2qnDo/2lV99OKs2ndo31/19zOy7arvb9ju91V97SyNoSrGDd6hl9Gv+rJ3qx+p472lYVTHOcAhKAGNC49jZ6YTOX4PwyumGP0b1rXN7h2eYGuoEgk+D8IrvRETus9gpT0doU6XEF3eh/m9E3UucQWLHVkIc/FGasMo1o5UX2VFy0BERERERETW470HnnsHONpbxWRLJrwuXoS9kyOcnZ3h4uwIOyc72IfH4XLPpHZBVzvpV68/2N3B2tI4qoqy4OvsCXsXe1y66ABnzxjktwxgRi5c8oT1vnYnAs/o6Gh0dXXhZz/7GX7+859rwZM8ZqnsB3W7A08ZoTk6OoqmpiYt8DRqaWnRRnvKCFDT7U6CThkxKMvZ0dGhBZ7r6+s3vbetkrBTAl8Z8Sp1MD8/f3OfYwUkjJZ1IyM8ZfrkBx98EBcuXEBRUZEWcJpOxXsnpuW1jsBzT79u5huQ4O0KOzs7OKm+X/p/jdoXOLm4IbJ8HGuqT9dGLMrF34NdbMz3oLM6Bn6+9mo/oco5OsPJwR++0Tmo7hrCmoT9hs+QC7ybq4MoCnCEwyXzz3BSn2nn6oO4uhn13oc42t/AQncuvBw9EVQ0pH0/0zBv//AQu8ujqI53hqNvOMrHboyklJBnb38N8+N1qMwLhIub2n85u8DZ0R7Odi4IishCVdcElrdkGQxtUn3myd4iBitiYecYgrSmWVw5OtA/d3CEq+tjaEz3wkM+Cagc3saJXBiXzzo8we5sBwrCzsM5Kh+di1dxrL7bye40WnJCcM4lFsU9y7h6bHgvjdovHh1ifaASCV4PwSO5CoOrhtfpxlCTHgKHc+fh4Ox0Yx1oHGF/0ROp1X1Y3D/BoYwg3RpESYwXHvbNRtvkhvrO+/rPkOfHqxDndwGOSfUYXd7HsVl4t6/29/NozAiC6/kH8VBwMQbmN3FkfL0pVfcHe3OoS/CFe1A+euY3sG+cxWGhCUl+bqrNXIKj2Xc1coCDvQOcQkowvLqlBQAHezvYmqpGtLsz7OwN7cDJSbUBe3j7xiK/tgdza7rT9S2B5f7BFpZVPbeUR8LbS7U1VTcy7bSznSN8AxJQ2NCPmTWZOtN0GQ2v3ddhbaoZ9ZdD4e5hr9qC+jxHF9VWgxGcfBktQxPYltG7++r4py0L3ufP49xFR/ikl2BQJ9/3xvudkuOlw3VMdGfB3/lBfOpBd4SnNmD25Og0FNk/2MfO7jJmRypxOd0Hji6qHTqpduig2qG9G0Lj8tHQP4M1nb7s4ckepjtKEet+QbVBff25yDblYKfqUB2POekfc7S7APeYIrTPHOPxgwnUZYXB8dwFtVzSXtRyqTp1cfRBTFo5uieXoZM60JZhD0fHG+gtioanRywq+pewf3KoBS7bQ+WI9bmEgLxOzO4+joXGRAQ5OCG5fhTL+ww86b2TMG57sBTR3pcQVNiNud3HMFcfhwAHF6Q2jmNFtad3C7L2VT+xtTKK4eZURAQ74ZJsB7Ld2vvAIyQVlxu7sLilD/T3t1Yw0Kv2XUGq31R9gqM6X7lw0RtRGRVon1vDjuqnLP+Qw4TsX2R/NteNjqpo+PoY92dqe5L9WUwOatT+bH1HfTfpDzcXMNFSjihvL7VNy2eqfZp/EFIa+jC/rvou2f7VZ26vzaK5tgghHr5q+1T9t728byjSK9sxosodaJ+t+hK1v5tuz4afWwBSmxf0wevZ72hC6nhf7f/qklzhFJyCluXHoZvuQI7vefjElWFo2/oCz53RGrWvuAjfzGZM7X4Gy21pCHV0QHzVgH5/tq/2Z9sjKIv1hntkCfrmd3B89M71QERERERERB9N7z/wbM6Au4MLfBPSUV5WjvLyIuTlxMLP3R72bqHIblnA3pF6/cExTlZH0ZYXiItuwYhIzEN+VRFys2Lg42qPh5xDkVY3icNjK72fDN0WdyLwFDKNaEJCguZ2379T3Il7eEogJtOgSlBVV1enBZ4SojU0NGiBpoSiYmZmRhv1KI/39fXddyM75+bmtBBXlk/IyFcZ6XpTn3OPST8oI9llHZWXlyM0NBSf+tSntMAvPj5ee0y+v4S1UtbSe3xYVhV4zjUgwccNDkGRyLtcjLKyMpSWlqK0pET9WYaWgQ1syQ9eZD3LBemFLhSEOsHOyQv+YWlIK1ZlVfmitBSEBgYhMLAAvRvb2JX9jRYA6bA+34B4Jxe4ecejuKRU+4zy4svIjwrCRWcvBBQOGC4Ab2KhJxfe6r3PBp7atKa7yxipSYL7ww/B2S8CFYbAU0be7O+vYqwzE0HuF+DoGoyw+Gxkl5ehokjtnxLiEeChvrOzD0LLBjC/KyN11PuaBJ72TiFIa7458GxK98bDvpYCz04UhF2AS1Q+ukwCz9acEJx3jUVxr3ngKaPsDtcHUZEcgIv//u/wS6sxCzxrU4Nwydkbsdn5qFRtUFsHmhJcvlyN/ol56GSKWPWd9YGnN875ZaPdJPA8ODnEeGUC/B3OIapcLee2XFDWf75m/xh7I6WI8nXGRdXeL10KRUn/PDaPjIHdDTKt5N5sHRJ83RFc0IuFzX1tVKLWZrTA0x32ARHIUW2m3NhmRFkpSooTEOnqDJfgmwPPKA9XOIXGoFC1g3JVvjgtFaH+brC3d0Vo4SBWd1SbkUDjYBuL4xWI87eDg7MvgiIykKHao7TLy2qfE+rrAWcHZ3hmNmNkQwIJw3dX31tC+eWRaiR7XcJFlwCExGQiU2tzRchPjoe/TxAi46oxfqSOZ/bXMNWaBW87dazjaAdH9xBktS7j0MJF9/3jI+jm+1AW54lLTs5wOu+OsNTG08BT2uiBak99DYnwcb4IJ7cwRCbnIa+iHJWFhciMjYafq506dgpCXL2EQGpdqnaxMjOCpspCFMm2VF6B8px4RHieh6t3FDJzK1WfpOqpqBCVjcOYXrmK63vjqM8I0dpLTFYeKtX+rDwvH6lRIXB1OA/H4Dy0Tm7h6Fi1i70jHK/34nK0JzzjKzG4fKBvx/tHuDLbiOSgAMSU92Pl+DEstaQi2DkIeV3T2Lxyc5sguiXVnk5m6pEQGIC4qkHVnh7FYlMSgpyCUdgzg63THwXcgupvdzfGUJPoDUd1LuIZoI7/CopRrPrwssxMRIUHwdsjFY0zK9g5PoSuJ1vtP33gGZiEFNUHFZdlICpMvdbOAQ7RNZhe0+HA7MceZ+n3Z5tzHcgPdlTbszcCwo37sxJtfxas9mdBwYXolx/87G5gvjYWAY5O8AmOQIbqT4ovX0ZKkD98fVS/XT+n1cHR9hLGqyJh7+6H4KhMZJeVoLAgEYHezrjg4KX6uH7otBGo6j1Vv70+04Fsf3cEpjZh8eDwnc+bZJvdnEJHbjg8IwowuPOoNsIzL9AVwSlNmLW2bVadL15ZaEVGaAAiirqwePw4VjplNKcfslomsKG+74FaD4fHOoyUx8HHIxKlvfNq/bLvISIiIiIiopt9gMAzDa5OAYirmcLJ8SHkvmVXDte1Xx97P+iIwPhKjB8e4kCdwO4uDKOjLh+lwwvY0u4ZdYSrh6sYaUiD2yedEZbeiGl1wqpdUCarJO1AQktL5H5Dll5jSsrd7sBT3keCzqioKE1cXNxtDVPFnQg8hWxbMrpR7ucpoz1lalsJPiU4kylThfy9ublZC9vOTndrq2QZhASbxjBXSB1IXciIVkuvu1eM31e+q9wfNigoSBt98dBDD2l/hoSEIDg4WGsrsp5MtwWL/ecHdGcDT/2FXLm3mUzNa5E2DaghvJLA09cdTomNWNxQ/YKM4pPAyeBG4KjKr8+hNtkNDs6eCC4ZwNyuTBuqL6+fFnABY91jWNzWqX2L+rdMKyrTbw4VI9DVEz55fdhR+xy5t9nx7gYWGxNxycULAZdNA888+Dh7I7jYJPBU73N4KCFWDZI8LuDipUtwDYhEpRZ4qtcd6bA8XItYl3Nw9IpGcfsCNrV7pklwdoijgx1sDNYgL+ACLrhFILd1UbvYfBp4VsapZQpFuqXAM8MH5/wSUWUh8CwMvwjX6ALzwDM3VH1GHEpMA0/1OTIycLAiAQEO53D+wgUEpJ8NPANwzisN9SMbuC4Xrk3WgX49GNqeIfAsjfXBef8cQ+ApnyNB1jgq4/3h4J6O5olVHJz54dH+8R6GS6Lg4xaI9Iw4BPk4IaiwD/MbR6rub5TTt6E9zNYlws8jBIW9qj61MM/QZub1gadjfD3m13dxctpmpN2pz9zpQ56vJ9yCijFkGnhOViPK0wNu6e1Y395XdSJtcQ/bs01I8HSCi2sSmpe2IdNa6hZ7ke3voNaLH9KrZMShakvqfWQUmLTfnelu1MS4wt7RCzFl49iS9qm+m6zzrbkBFIRdxEW3UCQ0TWNdfSe5t6X+vuO72FqdxWjvpD5w3F/FVHMGPD194Z+k9jeuHghSxzDze2cvuqv6PVnHZFsm/DyDEZWdj3S1vYakGAJP1UaPj7Yx01mMUPsH4RyQgpqBVejkWEjqRtrh/jZW1POpXg/hvFcCyvvWcHhs2Ba1+lPLeHwV+zNtyAu5ALf4UvStXtcCba1+tfpX7WVHAs9AnPdUnzG0rm8v0l7359CcFw7HB1yRXD2ApeMT7T6f671FiPby0kZVLR2cqHWhludM4Ll09Ah0/QWI8AhDTsfUmcBT1ataVzcdK2gBvLGMIvX/ocpJXZiWk35F7mF7c7nTMoZyWp9yppzcX/Xdy+nvq2paTpsa22I5wzb4LuXOBm3ygwzZl5iVU/8+e59fy+WkH7NQTn3O2XLm98GVH5tIOZMytyyn2qalcqbr7BbljmTbN7Qn08BzWbWn7b58hLuHI6972iTwlHWv/+6m08Ae7mygsyAY7o52cE9vwdC6Knfah0v7X8FkzyhmV2U66j0sdRWioLkT4zLFs9aPqDLLbUjzc4OjfSzqZ2VqamP/J+tJvq+qc8MyybrbXZtBTaKL6mO8EFI2hPnT/Zn0Y3vY2ZL92TiW1eM6te+ri3WCu3cyWpZUX6rqQu75ebC1jPHmAlzuWlR1oOpsfQEjTTko6JnAqryP2i5PDrex2K/2gTKCPLQIg+r99D8gUnWyPoOOnAB4BKaieVH1TyZ1rl/PhjqWx84Env26R3C01I/ymAAEJdVjxsoDz4Wjx7A7XIIYT7WvbRozBJ5qOQ+PoRupQJyvB6JKe7Gwo5bZbH9ERERERERE9CECz9jqScgFb+3eWScHWJ1oQqrLRfhEXUb/lvFigfHinP4Co1ysO7x6gKWhGiQ6nINPfAkGNk84HZqVknUmIw4lkJIRiDLFqtHI6ChG1WOWXmdKLlbd7sBTRnTm5uaisbFRU1JScttHed6pwFNIvUqQKSMDZcpa42hP44jP7u5u7Z6QxrJnX29N3s/3k2WSgNM07JRpbZeXl61yOWUdyTTCMnWtrCfj/TsDAwO1YFrCW1mHMqWyMZg2rlth6T3frzsbeOqwtbKMZbUcsiwWrW1gS+7LKRecjYFnQgMW1nf1oYNhmU/Xn9of7Kv3XW5JgruLEzwSmjC7JReuzctqZL9g/C4SWEjgOVAIP1dPbSSnTi4qy4XznXUsNCS8h8BTH47sroygKskLLp4BiA7xhqt/pH6E5+ExjjZn0Vvgj4cc/BBfOoJt+dGO2Xc6xMnhBqbac+DzsD0CEyoxdnCMA3n8jgeexqlsKxAb6AqfgBAEeTnBL9V8Slt94JmKuuF1XDs5vPHdDbTvpNXpLQLPwys4mqhCgp893NKaMLF6cNN0tsd7IyiJ9IZLVDUmZvpQHuODSwEF6NemtTUst/YZe2p9z6Au0R8ugbn66WwltJJ9v3wXY+AZV4e5tR21DMZ2oNqJhEe6XuS+U+CZ1oY11X604F21hT3dBnpyVXl3N2R2banXb2O+PhaOTq7wT+vAovpced/T+pCg6UCHtbEaRDk7wMM3C92b6nG1zo62lzFaHorzDp4Iz+/HuvpuxmOfs0yPf9xdQxFX0oqePB84+kShdGQPx6b3wZT3XlPtIdkHbpHpqGxrRoqz82ngKT8GO14dRWO6Bz7pEILMhmnsXrm5HV45WMFgTTLcPuWAiJxmzBwZjpUMZfaPrmBvqhW5EnjGlaB35ZrW7rTXa+vGNPBMRvXg2ml7OTi5htWeIsR5/hu80xswsnYd16+uadPZurvLdLaL2ihg7X0kPJmpR7yvNyJKerF49Ch0vTkIdg9Dbsc0tozhidSRTPu5OI/x0RG13x9SRtRxwiimZlewvS19pLyfbL87WFuYx9iIsdywdjwxPbcKnfF+slo5HVbnZk3KyfuNY2Z+DTum5fZUnzM7o8oNa+8lxsYnMLuwrvpiVU47FlXldrexNDON0dNyI1q5ucUNw/pT5SQo393CwvSUebmJScwvbRrqVtqZaqu6TcxPTWHE8Jn6clNYWFZt2bTc9gbmJidVOf2ySrnxyWksrahy2vGvWieq3P7WOmYnJk7LjWjlZrC8uq0PC6WfVOX2Ntcwo47DjHU3rOpnfGoWK2tyP2C175LjclVud2MV0+NjWrmhIfV+qtzE1BxW103KqXavW1vGlKp/s3LTC1jfMJZTdafKba8uYVKtT+1zpZxaz5Mzi9jY1N8zUyun+pKt5UVMqGNE4/eT48XJ2SVsavemPMbJdA1ifLwRZQjQt3uyEeQejvzuGWwbR0Gr/cHy7JR6nwnMq75BJ9u22i521D4i1NsOl4KL0b+4rf1Yw2zbEWf2LTd+BCDvobbx/UU0J/rAQ+0HCvqXsam+t1a/sq+R+4GOq3WzKT/GUetOtZnF5kS4qv2ZV1IL5nSyriz0E+p9JcDeXBlEgZ8jPH0y0a3OhY7VPsb4AxDtfEg+x/Dd9FNqG56TNqCWZXOhF/nel+AekILmJf2y6fd58sPSTPi6BCKteUHVo77P3pP+cmMJ06Nj2rpY31HvpfqgK5uTaMsMgnNwLnp1j+JosRclUb7wT27EvDUGnvOqnwxQ+/OCDswfPY7dwcsI9whBRtO41scYZ1o41g1psxa4R5Rq09re9KMGIiIiIiIi+sj74IFnzaR+hKdcCL56gNXRakTbOyIwsR5z8vjp6wwn+UKd1F69uof5rkIE2dkhMK0OU7p3v18P3RtyYU3CqIDAIHzqwYdw4eIlXLxkh3MXLuLBh88hJSVVf6HmbFsxcScCTxlxJxfk/vSnP0H+e+SRR7THLJX9oO5k4CmM9SZBsoR/EnQaQ095TKeTe9Tdul6thXxPGbFqHKF59jsb/206Ta+E1DKC1ThdrzUvp3w3CRUlhJY2/O///u/aiGLZLmS5ZZmkjUhwK+VlOSsrK7XHJQiVfu/se74fdyzwVMu1tz+LrqxkxAaHIDQiAhFnyL4gPFUt28omdiXkOh3h2YylrQNcOTnSjwIVEoiq95W+fle3ho50d7i5uiGrax3bxovJZ7+DKbmQr1vHXEMCnN29kdi4YLjAfYBD9X7z7yHw1EbS7K5guDIe7q7hSK3tRneO5+mUtjICRkb0FQU/CJfABNTPWB4dsn90Fdtz/SgOexCOgYmomVCvlbDxDgee2lS2a4NauGgfXIjG5moUhl2E55l7eOoDz3Q0jG3h0Wsn+vqXUEX22ybLYR545qFrRodHrl/D1aNdDJZFwcPRE1nNk1hX399sH2yYzjbS2xmRlaNYPtjH8OUIeF7yR073DDZVPZ+OfpL1Nt+IxAB32MfVYmpZZ7gAbdgvmASes6vqudNgVdrfHna23z3wXN1U+yJpX2q97+1uY7wsGO4e7sjs3MbWxgpakpzg6uGLwgGdFuCYjRCU76iWb2djEa2pjnD29ENur4wMPYZuZRJVkefh4huGinH5XPWdTF5nxuT4x805CIk1g1joyoWngzeiSkdwcGIMgfdVO9vBwmAFohzdEV3YhdFJtd043gg8j45OsDbWikzvf4NbZA46pE0cnPk85eD4GjbHWpDt/29wjsxD29yJWTmtbZkGnstn3uemwHP1dCTx3tE17IxUI8X/U/BMrcPI+qN4TDeAkjjVhv1z0Dq5eaN9q2O848VuberOvOYxrB5ehW60BlnZpWgdV/23Kqf9mG1nHYujbciKCYeLqxc8vX3h5+sNZ4dLcAstxsjcphboH8j2PNiEtIhQOBvK+ao2IPci9YqswNTStionIeEKZvrqkRQWBGc3b3h5+8DXR5Wzt4efamvzqzvaMcrB9hImumsQHxyolfP28YGPt2pz9k4ISm7Csmo/h2rbONhawGh7BaID/FUfo8r4+sLbyx0O9i4Ik5HEOmln6jh1cw6DzSUI9/XT+iIp5+XpCnsHtT5ze7AtP8SQkGpjBr11lxHi4wtnD/XdfH3g5eEMO0cvJF4exI7quw5U/7K3OoXOqjwEeqm6UOX8VDlPdyfYO/khvWxEqz9te1qZQGtZNvw9vOHiqerOzwcero6wU+0tt1Zu/6Df7nTLo2goyoCPuxdcVLuXcu4u9rBTfV5R04xqf6ofUdvQ9uIwavJS4OXmCVdP9bmqnJuzHezdo1HZPo8j6b/lRy+qT6zISlCfpbZDQzlXp0uw90xEfe+iodw2NmZ6UZIap/p1Yzn1PR0vwdEnFa1DKzjWym1hdbILhUnRah/lCXcvQznVBpz8s9EzvobjK8c4XlB9YmoK8lvHsXqg2pNqi5nZZWifWDW0p33VBsZRHuaJC/9sh6Qmmdb5ROtbhkvD4eN4DjE1E1jeOTMVt0XSFxnOQWR/cqT6/e0xlEZ5wMk1EtWja9CpNn6gth3dVifS1LJfeNgXl4dl5OcR9nWraEt1g6ubB3J6NqC75f5M9kF70K2PoybaGfbO7kiuHcfsimqnMvpSRoSe7WPk38bvpj7r5MoBNlV/Ee9uD4/wfPSvGQJPqY9jndq+KhB5yR3BGW1YNtTT0ZUtzPQWwv9/PgCX4Cx0rsmPKqTvn8NAVRbis2sxpruKw5VRNBVnI6duFFvaa02+x722f4Tj5T6UZaQgu34Iy4fXsTvegNzsYjQOLxnahJRVy3syj5b0MLjYxaBycBG7xh9mEBERERERERl8sMDTMQAxFWPqRHwHuu1t6BaH0Xo5Bq4eEUivG8PWoemFVx12t7ewrWxtrWFtvA0lCT542D8RZYMruMJf51o1uZi+urqG4JBQPHzuvD7wPH8BaWnp2sXGdwur7kTgKWGMhILG/x5//HHtMUtlP6g7PcJTRs7KSNnW1lZtWlvjqEcJPCUMlODsdo0SvFMk7JyYmNCCSxnxKKMdjSMd5Xn5U0g4KPfpNC6jjOwcHBy0+rBTGJehqqoKFy9exLlz55CXl6f6s21t9KfcY1Iel35T6iAnJwef/OQntfYo92uV7cfS+75Xdyrw1F9knUJTVjKig0MRZgg5Tcn+IDy8EJ0ySkouOBoDz9gyDE/NY2V5EQsLC8oiFjdkBI5M5yvT+42hPNQDbi6RqJrc0C78v9sFSRl9tbe1iv5CP7h6BuCyMbx6r4HnvoSSqq0NVyLe1Qkh6Z2Y255HR5aHIfA8wvHJHlYmGpHsZAefiAL0bd0I7sy+y+Ex9pZGUZfsjAs+MbjcuwGZVvKOBp4ncjF/DQPlMfCx80d22xI2F1uRFXjeQuApAVY8yromsbG2rF8HahtbU9ujBEoS7mjf6zTw9MUFv1TU9U9jY2Ue8x2FiJB7YSZWYWRJd/pdjQ5O9jFSGgkv50hUjixi9+oVbA0XI8bbHq7x9RhfkVE18hq1bajP2hm4jGAfJ/jl92J+Yx/66Tz1282HDjzVetzcUcut9iPHqo4O16dREe8MZ2cfXB7exMb6MIoCXOCm6qNh3tBmTJZFSNvY21zCwOUAOLj7IqFhAftH+9hY6ESWhwM8AzLQsar/vrdsp6aBp/zgq34KOwvdyPdzhWdEMQZ2DKHV/hEOt+fQUxQKd+84VE7vYGOsFvGngacsxw7m+soQdfESApKqMCqhjcV2qNrOXDeKo+xwPjAVNaPm6+r9BZ6pqB3Z1AfkRye4dnKA8YY0BNg9gMCcZkzsPIbrc81ID3WEY3wlBhYN9+88fS8JcyTAMzym6lmb+tfwvffU37cHShDp7QansGjkNnRjYHgKU1PtyAz1gb1bGlqmVrF/5QBb3fkI8nCHa1Q8Cpr6MDQ6iYnxFqQEeMHeKxtd8xs4ON7DalsW/Nzc4BGXhKKWfgyPTWBsVPVB3h5w8i/EwMo2Dg63sdSUCk9Xd/gkpaKkdUgbAToyWItod/UZoaUY29hR62YDs7UJcHXxgF9aJiraR9T+dwyDvZUId1afEVWFKZ2EtisYV9ugo5MHAjNzUd05hvGJUfR1liDIwQ0+CfWYV+3pcGseg0URsHP2QmhuIWq7xjE5OYrulkL42bkjMK0Vy6rPONyYRnduCC66eCO8oBgNPROYmh5Ge302vC56IiynC2tX1DpZG0OrWk8XXHwQVVSGpt4pTM8Mo6UyHW7nvRFT1I8ttR0eLQ+iNtkP5938EFtahda+KczMDqGhOBHO5/2QWD4M3fWrOFroRVmcN857BKjHatGutv3ZuUFU58XC8XygOk4fx66Um21HQaQnLngFIbmyAV0DUq4fFRmRsL8YiryWKeypcgdTTcgM8cBFvxCkVbege3AaM3O9KEkKwSW7SJR0z2H/+hXsj1UjSX78EBiGzNp29A2pcrPdKIgNxCWHOFQNLmLvWD/K+J3akwRbB4dzaMtPRXRALMr65rC+L6HhIprTguB+wQe53bPqsTM/1riFvR39Oci2bh0bSzMYq02Bu6cX/C53Y2VLH4jv7atjmu1hVCbEIjoyA01Tm9hR33FncxSlIe5wc4tGzbRMk3tzH3NKLYeEvmv9JQjxdcKl83YISKhCh2q7c8ubWrBqHtCqYzyd4fxoex3r0wNozglR6yMMqa0z+u+lLd+eNrX62kwHsrwc4BtZhhG1b5TpsQ+PtrE41ohM/1Ak5tRgeFNGi+tfI/tPbTSq9ln6HxCZTnusrQf1GaaMPxh5f89J//lenjN93Pw57ftZbBMm/ZAqI8HvUHkcfC/6ILt9EusnVjZalYiIiIiIiO659x94tmTA85IH/CLyUF5ehvLifGSGe+PSww7wSqtD/9oJTowXNeWEfH0O422luFxyGUU5MQjxsMMDdl5IqO3FyrWrOJITftPPIasj94qSEXzBwSH6sDM9XQtybmojFtyJwDM6OhodHR344Q9/iB/96EfaSDt5zFLZD+pOBZ5SZzLyT+qkvr5eC9Ik4JTgUMjf5bGWlhZtCtj3Usf3gnwvCW0lvJTlEPJ309BTSKgpwZzpyE4ZDbm4uGi1y2ZK+kJZX9nZ2VqQaWdnp60feVy2C7l/Z0BAAC5duoTY2FgUFRUhPz9fqw9Zdkvv+X7csRGeGsMFRrUtayMELdLvC7R1NdeIRF93OHq4IzgsVB+Iqv1FaHgEImsGsbK9pwVhus0uZLq5w9U5Ax3rm9g9veB6a3JhVrc+j4Z4F7h7J6BxQaYTVK9Tj7974DkMuT/e/uoIKuPd4BSUjLYFtW/ZmEV7pjHwPMbJlW0sDJci9JMuCIyrxaTpTASm30ULPEdQm+SM81rguX6HA88VPHb9BGsDFYj2sYN/ZhNmdj+Do8kGZFgKPNND4eDgAJ+QYH0wrdZBSFw8Miqr0D0ygVW5L6qq89PAMz4Q9k5O8AsNQ5SfE5wuPoTz3rGonVnC7tVj8zpQdXugG0BxuIf6vlUYXd7D1eMjHJ0sojEpULW7eNSPq3Z9JKNqVLtQ28FSSxoC1X49pnoSS9tHhgv6hjbzoQJP1YaSazAxu4jl5SUsTQ+hrzQKdhed4RFaidGdbWyutSLF0RUeXnnok+WWC+imy6MYA8/+QrlnqT7wPDjewepsLaLPOcMnuBQj2oX3d+iPzAJPf0RXz+CR/WWMVEXDziUEma1Lqj/Yx+HJMdYn25Hpcwl+idWYVut/ZaTGJPA8UdvsOsbbc+D3CVdEZLVi/qphusYz9G2nC0WRdjgfIIHnjXZ1+vx7CjyDcMEjFiUd49hYW1F97zwWe4oRF+CIB85Ho7hrBrpHHsHOUAUS/c7BL6sF4+tXtOlpT99LPk/6gTP/1v9dwpg1dOWFw+NcCEqH1H7r+hXVDlT7O5lEdUwAnLTAcw2HV9fQlhYItwtRqFb/3lPt71BGZh+OoizUB85eOeha2FTvt4TGBF+428ejaXEL+1eMI+QGUOjvBVf/QrVNbKt1O4uaKNV+nFLQsabDgYyglR/RbXUj28sT7qFlGN+SUGlcvb8b3D2y0av6qUNp00d72F5tQ5qrBzyjqtU2t6v6oEH1/q7w9C3AkPr+R4eq3PEuNmQUs6M7fBMasajef2tRvb+nM7xDSjEuIyplRN3JLlZVu42280BgehtWTw6wNt2KVFcn+EfVYPrqiapTVe6qDotDqh+SwDO3G5vXDrEyVocEB0cEJTZiXtXd0b7qb65tY6a7AAESeBYPYOfRIyxKH3HJGeEZbVh6VK1vmW742ibGW7Lgc84PiRUj2HvsEHOdlxF23gXRBT1Ye+yaKneIK9fXMFSTDE8JPOsncPD4AaabsxH4sBsSy4ewocodaeVW1HYWp9ZRCHIldHt8H2O1ah/0kBfSG8axpT5XX24JnXmRcLkUieLueRw9touhsnh4P+SHnPZp1aaknCzHHJpVn+VsGnga2o/l9mSk3z/JsaZ+WlcJQcdQHu4PpwejUTW+oJ+S3Ow1lm2NNaG6vBhFxRnIiFLnKxcvwSkiG10Shsux7GlZ+Uxpj/qRlftqG9je6ES6q8xYkIWu9a133Z/tqb5if28bc/1lyIgMgrerPS6dV/1BXCHqe+exotN/Z9m37W+vqv1YJUpKilBckIhYf2c8eMEZwXn1mDk+UdvQjTqRUelbCyMoU/sSz9BsdKyeGWmvluNGuGkk/ZrJv03rXD2+s6vTfrxltLWl06aKlsBUJ6N/tyw8J8Gwhed238tzOxae06actvD9FEt98v7RCWabUhDs7ID46mEs7ak+xHQZiYiIiIiI6CPv/QeerZnwtnOCm6/hYqsSGRGOEB9v+HhEIa9+DKvb6uRbvUamkttbmUR7cRyCQ8L1I4dCfRAQ4I/YrDr0TcpUUu8++ofuPQl3ZCRXWnqG5fZxC3ci8BRyz06ZWlQkJCRYLPNh3InAU+pM7gcpIwFlVKdMYysh4fT09GmZqakpLRSUaVFlGlUJ295rXd9N8p0k8JQQU8I94/1U5V6XMuJMnpcgWsJNCTuljCyXcWSntY9eNZLQT0aoSnv713/9V7i4uGijVWV7MD4n7e9//a//BW9vb+1+t9LmpW7Eh13OOxt47uNQfdeTk5N3ICNoDNu7XPT3dYeDiy9CJOSMjDTsA6IQU9KnTT16qAWevcjzlsAzGc1L7yXw3MO+et3W2gAK/dzg6V+AAd2OFojJxeN3CzxDSsfUv1cxWpUAN6cgJLfMautgf30GbWaBp0wJWImoc07wj6nA2MGtA8/9Zf0Iz4u+sSgZ3L6jgWfp4AYe0w1rU9na+WeiaWoL11WfszPecOvA85IrfIPDERWl1oFaD1HhIQhwscN5ew/ENvRhce9QCyX0gWcAHOzc4a/2wdHREQj2coZnQJQWgK2rdSujbG4s+yEWWzIR7OaEmIphzG+q/bNuW5teeLo6Tn2GCxLqx7Gyc4RD1Sa0wLM1XQs8o6smbl/gOVWDaE9XOHp5qrYWhvCwUIS428HO2QMBEXmoHlXfVbWrrdUOZLhJ4JmJzo13CjyXMVAUAEcPX6S0rODgeBdrMmJZHct4BxViUO57J9/3zGtPnQ08qyZx9doeFoerEGXniMCMBszvq3V0tIaxpmR4q3aY1rqC69dV/QxXnwk8NzHZmY+gB5wRltGEmeNbB557hhGel4LTUT+x98ECz6xwODo4wDs4SG2vUYhQ68PNyR7OHuFIrRrDzNaJ2l5OsD1cqQWevpnNFgPPW5PAcwt9BeHwOO+JjPZxbKj2e+XKVVx/ZBa1cYEmgecWujID4HrBD3l9M9gylLt6dRIVYb4mgecaWpO94WIXjOLRRWyrclevXsHJ0QiKAuS+vMbAcxH1sW5wdoxE5dQKdrVyJzjc7UOut2ngOYPqCGc4u8ahbl7tU9VnXrt2rNqFhFnGwFOmIx1DSZADXLxS0Kze/0DKXT+CbqUFSaeB5wG2lvqR73NJfY8sdEq/py3rITZn6xBzGngeYmOmE5keF9X3KEDvjmpDUu6xA6yOlSP8NPA8xtp4E1Kcz8MrqkQLWo9PruGRx/ew0HcZgaeB5wmWB6sR53ABvolVGDuSPu0aHn18B9PtOfB92Bh4nmChuwSRly4gIL0BUydXVB1fx6Of3sZYfSq8zhkDz2PMtuYi5PwlhOa3YlbtS/TlNjFUngD388bA8xiT9WkIOOeAqNJuLEgda+XW0VMQDdeLxsDzEKMVCfB52AXxNQNY1srJciyjLSMMLmcCT8tt6QzpY4zbpRbqTaIqJgAuD4ehdGQeW0fvEnhqr9/FcncRkmLVeUqYnIeEICTQHYFR6ShrHsfSlnp/023/9DONgWcPcrwk8ExF68q7B556sk87UN9tAUPNpUiPCIS360VccIpERtMSNlU/JWGu9EsjtSmG2RTkxyv+CFTtOzy5FK2qrjbUMhvfUx94DqNUpjkPzUGnSeAp5DubhZvvRL3v0d4KJocaUVB4GcXFxcplFORXoVVG6x6uYry/HvkFps9Vo6NvHodH6jv31p15rgbd6vseHi1hsLvmzHN16B1Z1kbn9nVUn3muHv1jS9qU+e+1TUjgOdMogacjEmoYeBIREREREdHNPuA9PAMRVzuNq1fUiebhEY7lYvVYM4ojnODgEoSMxjnsnk5Vq07sZZTO4SEOj/dxuDuBwdpUBNs5wD0yHx1LBzg2ueBK1kvaxHsd2Wl0JwJPeR8JmSRwETKy7naGqeJ2B55SZ/KLdqmLuro6LeyUgFBGCJpOAyt/lwBUwkEpI1P3mj5vLYzLI4GmhLbGEZzypwS1Mp1rf3//6eMyYlXCTglBrW1Z3om0d1lHoaGhWuApozllHWqjTlQ/KXUgIzrl3p6+vr7aMkqbt/ReH8SdCzzl4ug65idGMTwwiMGhIS2svcngJBY3JUhS/fnpPTybsLR5q3t4ypS2c6iLdYObSwBKRja1e569W+B5cKDDxkwtomXKyZQWLMioD3nPdws8XXwRXj6s3UM6wV3u2deCWbnQrPZL+2umgadMaSsjrmRKwPPwDM1Ex4rl+0fvHx1jZ2EQ5VH2cAlJRdO8TDd7eGcCT/ckVA5MY6ouXpvKNqtxClvXjnCgXnfLwFPu4emdduMenhJ87K5htjkX8Z4X8SmPVNQOLePoyglOjPfwDMhD54wOjz26h5X+eqQHOeOcYygud05j68B44Vz69yW0ZoXC9WEfRKbmo6i8BMVFRSgqKUFZQgg8HS/BJbkJk6u72ki6Oxl4xni6wdHdX5tuWevro7KQU9mFsWXDdIjqvbbXJ1ER4Qw3z3BUTd5iSlu1fLsb8+jM9IarVzCKh3dxcHSIrUUZzXcR7v4JaFpQ27P6vrdspzcFnhOqPV3FzvIYauIvwdE3GmWTMuXoECqiHeEakYXOpSu4cnXvTOApU9oeYGmoFonOD8EnvhgDG1ctXrCXdrg91Ya8oPNwjy1E95lA870HnmFwvOgKn+BwREfJVNUJiM+oRPPIMrZ2JbjWv9cHDzyljo+w0F2IlEBHeMRmoKyrH4MjwxgZrkd2iDccPdLROrWGg5MTzLVlI97fEZ4JuajsGcDQsPQzNUj394CTTw665yXwPMJUUyqi/ZzgnVKImj4pp/qp/koke7vDJeAyBlZ0WiA1VpuACF8X+KWXoKFfvZcq19ddijh3d7iHlWNsQ32/XbXvrYhCiI8bArPL0TQ4hOGRAfS0X1Z9jjs8o2swrVNtR7eOvuJQBPp4Iji/Cm1Dsgz96GrJQ7gEnokNWNhX7WlzCV0FAfDz8UbY5Tp0DI9gZKQPHfVZCLL3RFB6K1aO1Da8NovWbLlfqB+iShvRNaLKjfaitSoVfpe8EJ7bhfUrqh0tjaMx3RNefoGIrWhGz8goRkfVvrU0EV4XfRBb3K/6hWvYnh9CTbKbarMhSKxpQ++oKjfWhbrCGLhf8EdSxTB2HrmO7dkebepnt4BwpNZ3oF8r14nq7Ai4XgpGRv04dh95BJuTbSiKdoJrcDQym7owIJ871o6KtBA4XwpDXusU9lW59dF65Ec4wi00Hjkt3WrdSjm5PUUgHO2j9VPaqnKrA5XICnWAW3gyCtp7VTlZ3mYURvvB0SkB1e838DSlts/9gw105gTDy84Z6W0zWNuz3IffRMJSbeSmcrSGtck6FET4qO/ugzT1Pps76nmt3zKnTdm9OYuaaFe4uQWhTPW5O++6P7vBOPJyf28OfY0p8HVW5z2+MvOBPGfcZxrOj7TpyOcw3Zmv2q4znHzjUTm5rZZPX+7dAs/3RUJ1tVx91RkICg7T/xg1IgzBgQnIrR7Gpvq+vRWpCDR7LhEF9aPY3p1BZ2nKmedk2ulJ6HYm0VKUdOa5FJR2zmB3exwNBYlnnktFhUzN/j6mpWXgSURERERERO/mAwaeAYitnsSx/CpXLhKq546v6TAv03T9myMC42sweaJOxuVE/kidyO7rL35q73l4guvbM+gqCMS/OoYgrX4KR8eGC8dk9W5qF+/iTgSeMtpOQiYZaSfKy8u1xyyV/aDuxAhPCS9lpKNMiSpBoNzDUwIzS3VqDD0lTFy00ulf5TvJfTxl/cp3NQ09Tf+U5yQ8k2mRrXE53omM5JRQ193dHZ/4xCe0qZNlBKs8Lm1bRuxKW5ERntJ3yr1X5bnbNYL1TgWe2r20DsZQFRkA94t2cHBygtMZjo6OcHRPRdvcGnblIrUx8ExowMK6IfBS61NjfF/Zd+i2MHzZDy4uToipnsXGnuwLzn4H/QgX7SKn2n8c7GxitiYSzu6eSGhYxI48Lxcx1XPvFHj6uvkiML0MVQnucA5ORuusXASW9z7Cnlngeaj2MyfQLYygIvIhXPKNRunwPq4enW2P+zi+souloUpE2l2CX3w5RnSyD7sTgWcYLnnFIzsvB6lBjvDPbMTUlkwrqX/dOwaeXqmoG1nHNbWf1a8D9dwjy+jMj4bbv/ggs2UMa9eu4qox8PTPQfvUJq6q9XhwfBWr3bmI8ngQdpHqvRd21L5cfV/1HodLrcgI84GHdxDCI6MQGSkXpoUEjtEI9nGBo2es+uwV7BweqfW6j8U7NqWt6T08DeH6wY17uklQsLu5io50FzipdpPatq7WkxyTGNel/nPk3nfbS13I8HKEm386Opb14cHe2hxaUhxg5xGAnM4NHGgjskxfq2jbiXrc5PjHGHhKCH58uKGNrvNy8ENC5SAWZcpkD2/ElI5iR9X10cnZwFOmUr2ilq8T+YH/rh+5OXWs1ouxXoz2cXJ1B9Md+Qg8b4eQrEZM752YBRzvOfCUe3h6pdy4h6fUo1pWuVeesa7kvbaGKtT2/bA2pe3E+ww8xb7cI7etAOFuF/HQQ5fg4ukNX39fuDk74JJ3JtomV7Gv6uTwZBeLjVkIcjmPh8/ZwdVLlfPzhouTI+z989Azv4H9I9VOj7ZVn5ACH8fzOH/eHm5ePvD1lXKqfwopxuDylr6cWgeT5fHwtFflLjjA3UcCRi84ObrALaIC4+s6tb6lXa1i5HIUXC+dw4WLjvDw9YWPjyccHF3hGVuL6W0JUw6xv7OI/txQOF48h0uXnPXlvD1g7+AOv6RGzGttSpXbmkWXqlu786qcvQs8/fzg7eUGOwcvBGe0YVltGwdqeffXJ9Cc7IsL586p93CFl5TzdMFFBx9E5HVhTb6b9K8rw6iL98S5h1U5Rzd4+/vBy8MFFxz8EVfcj02pO7Ud7C72oSLKDQ8/dE712+76cu5OuOAYhJSKYWyrPuHwitoHzXSiKMwZDz14Do4uHvBR5TzdHHHeKQxZ9ePYkR+sXDmEbqIZOar/efDB83B0NZRzdcQ55ygUtk5h11Bua7gWaX72ePCh83By81TlfOHh4oDzrnEo657Dnva5B9joK0eC9yVV7oLqz720NuCu2sAF92TUfpjAU/YJqq+dq4uDn+vD8M/rw9yWTGF8dtsx7Fu0fkLWleqnZFSm1k9KvyPhp6rz4SL4eTrjUnQNZmQ65NO+6QbpY/Z0mxgs8IWzqwvia+ewpfYF77Q/k9ccSfsw2Valv9ndWkFr8kU4e/ogv09fTs6P9NuhwcExrsiPV9QyPqTaUUhhv/6eoeq9bprSdkV9D7O+7v2SujCEraf0/cK7PXf6I1ZLz6l6OPucfhaBd3rO0vezbF/1n9qUtqrtcUpbIiIiIiIisuRDjPCcwTW5/5KctKoT0OvXdJjrzoHXA84ISmrA/NVD6FaXsTA9jy258GYYDXR89SqubY2iJcMDn7gYgISyYezIRVvTz6L7xp0IPGW0z+joKIz/PfbYY9pjlsp+ULcz8JTtSe7HKaMcZapaGeEp31/Cwpu2MxMSnkloaM1T2wqZulXCW9ORnkbyb1luubentX7/W5HvK32WLMPFixfx4IMPoqCgAOvr6xgZGdFGc7a3t2ujjc+fP6+N/pTpimVZZapbWe+W3vf9uGMjPNWy7an+fLq1EXXl5aioqtKCeFPSVqvaBrG+KReDTUd4NmN56wBXDX26kXbBUwKivR1sj5Qh2F0CjAy0z69j78oxZFpYKXek+oTjI9Vu1laxvruHg+MT7G9MoyLSAc6uASgZ1Wnvo4Ux7xR49hYg0NlJu6eou3MwUltncXggy6XWnYXAU2YjONiaRfflIFy46I7ggg6s7BxrI1UlvNJGSp5cwfH6JFqzguFg54fkmknojuW7qH3YaeAZhszWxRvh0ck1PLYtr5HAMwm1Y3t45KphWa88gsPFHhRFWAg8C6Lg7OQMF0cXuAfnoHFqC9eO9G3m3QPPdG2Ep9z7U/sOx9fwyJU5NGWF4NK/+SOndQKbZwPPyQ19SKvq9mRnCtXJgbB3CEFp7xy2D4+1EGe5NQPBzt5Ib53GplquE/WY9v4yk4Oqm8XGRAS4PgQ/tR7mN2V2h32sdmQh0NMe4eWjWNxSZW9n4JnWhrUttR0aAgvTNiw/tNrb2cBUYwLc7B3hmliFyZU9tT6lfanvIT9KUN/5RCf32kyCp70rgnN6sSJtX0KJ3XXMt2fB1c4RnjGlGN7awaG0U8PyHkm7ONBhU7XTDSl/NvCUi/fHh1ifake2jyv8A+OQmRoIR/9EVE1uqzYqU0bLtLfmgefBgarrtTE0ZnjjwUs+iKsYwNb+ibY9mbbDw+VhVCf64KJDGHLbVP95Yj6y7H0Fnp7JqB5cMwnITcoZ32u0GkkBF+CV1oDRVbnfpHmZd7av6nMT4w0p8PHxQmRsHlr6hjEx142cMF84uKejRQs81TLurGG4OgGe3t6ITbyM1sERTEy3Iz3QG47eMsJzHftq3R1tL6OvLBruXr5ITClG+/AoxiZakOTjqY3w1AJPqa/NBXQWhcPVU/WRGeXoHBtT/XM9YtT+2y2sDGPrqv9S5Q7WZ9CSFwwXzyBk5lSjZ2IMwwPViNBGeFZjantXH3qvjKMuKwDOXiHILahF79Q4BrrLEGIY4TkvU4Grdb+7OISKVB84e4ehoLgRAzPj6G27DH97D22E57IWCu1jZ64XRYleqlwEisqbMTg3jq6GXPgYRniuqbZ6pNr39nQHcmM94So/xqhqw/DCONqrMuB+QT/Cc1PV3bEqtzHejIxId7j5xaGirhOji2NoLk2Gq2GE57a0f1VubbgWiWFu8AxIRHVjD8aXRlGfHwenC0HaCM8dVU7ut7/SX47YYDf4BKWgpqUPE0sjqM6MgsOlUG2E566U29/BQvdlhAe4wS80DfXtA6rcIMpSQmFvH6WN8NzTyukw25aLYH/Vv0ZkoqFrEBOL/bgcFwR7x/j3PcJT+vFj9b5avy7/lu1wrgXJQS445xKNiqF56GQku7QraQuybznZh25d7Vt2dNjZ3cby9DRW1ra15+THSOLkZA9b3RnwdXfAhaASjK6otiR9jFq3B2r7O5btVPoxta0c7Kk+YLgUgW6OcAzIQseiOhaTOtb2Z+r9jPsz9Zkbck/MjUVMzSxie089Lt/L0A8dqP1RVbgdXDxCUTG5q/q+dSxNzWBdt68to3a/WLU/v6b2M6OlwXjYzh0BGe1Y0/o+CTyPsDk/gKLgS/AKzUfPpkngqfr0Q7UflX7vvY6U1NP306bu3XPvjfQNU3VJCHRwQXL9KJZVf8rAk4iIiIiIiEx9gMAzHW5Ovogs6cLy0gLm5ucxPz+HhcFGlCZ44VMOQUivn8TeI/uY665GZkAQCut7MDE+o42Mmp+dwkBdOmJcH8A5n2SUDa3g5HT6W7rf3InAU0YcyWhJ43+f/vSntccslf2gbmfgKaMJJCCrqanRSCgmIwPfy8UemU5VgkNZXglILZW512Q5ZESjhLgSAMooVgkJhYSgEgzK8lp6rbWRZZELlBLySD8oSkpKtOls3dzc0Nvbi7m5OW2K2wsXLmhtWkaAyr1kH374YS38lBGt0tdZdeCp2dMHTDI6Q/60SC4CGy5MGgPP2FIMTsxiaXFeqwuN2gcsr21iR72vNhXtziI6s4PgevE8PFKL0DA4gck5Q/mpcfR11aEkpxCtq+tYX5vBYG0KvC45wjeqFuOG6Wy1i+LvFHj2FSLQ7iIuXnRBcEor5gwzDsiyWQo8ZTTi4fEO1mZakeVpjwuOnogq7sHY+DSm5hewMDeD+bFu1GfGwf2TD8M3pRT9Kyf6i6mngWc8HJ0DkFjdh9WlRf3yLC5hbbwLlYk+ap8Wi8L2Waws6Zd1fmkF8wO1yA4+pwWenQsmgWdhNFwe/CTO24cht0k/la3xYvU7B54SYMWhtGMMa8vqO8g+eG4aM20FiPJ2wDnfTDSNr2Jf7sF6U+BpCFSPrmKlLQthbp+ER1Y7JtdO8MjBHBrSg+BkH4Wq4QXsnsgopRsXprWwYaERCQFueNjvMgYWNnF0fISD8QptSlG39DbMru0aQk1Dm7kNgafcG1Y/ekhfNzfIiCG5x94QysO94HDRDn5ZTegfmlLrU39cMj8xgK7ybAQ+rOo/NAVN03JsY2jT6rhDtzaGmhhXXLJzRFBBLTrGDK9V6252chidTeUovlyO3p0jnOyvYcos8JTRn2r5N2fQVRQCx/Pn8dA5L4RntmHlioQ6exYDz30JzE506vEaJDmfwzmXQKRUDqi+fgbTqt9YmJ3G3EgHKhPC4fzAOQTnNmBs/ao28td0+d9/4LmKq7eaTUNGli11IDfSDRfCi9Azu4MrN42cuzW59+vOQAkiPexwMV5tw6sHuCah0MkkqmMCtHt4Nk+pNnn1CNvdeQh2dYBjSgtmN4xTY4+iLNQHzl7Z6JrfwMGVA6y3ZcDHxQmuWZ1Y3pZy0h4HUOjvpd3Dc2BlGwdHO1huSIKHkwu88/uwvithllrGrW5ke+nv4Tm6uaP6sS3M1cTCyckNAaUj0O1LuX1sr7YhzXAPz6kdtb721jBZGgE7J7UeqybV+j3GyZU9bKh2n6jdw1Pu1Xqo+qRFDBcG47yTH+IaZtU+Q8rtYnWqGtHaPTxbsaweO9qaRU+2Hx5yDkZK6yKuHJ/gylW17odKEabdw7ML61ev4Gh9Am1p6vjZNRzZ3Su4KkH9tW3MdhcY7uGpn9L2SEaBJrjhAfcYXO5fx3W5J+z1TUy0ZMHnnNzDcxi6R67jeLEP5VHOeMA7CZUjW3hE7SeuXF/HUE0KPM/LPTxlSltVbq4DhaGO+KRfBhomdIZyK+grjYPbBbmH5xT2Hr2Ow6kmZAba41PBeWib2TGUW0JnXiRcLsk9POew/+g1HI7VINnXDg+FF6N3cQ/XJYy8Nofm9FA4v997eKrtdHNpEmNDw5he3tTuIyx9yv7hJkYqEuB36UE4yH04u0cwLvsW2W6nJjE82ILy7FzUTy9hY38J9dHBSM0sQWffBOZm57Ggyk0NtaEizkn1Gc4IKOrBytauFqru7qxiaWpYHbOOY35DAlN9P7WrW0BHZgCcL12AZ1oJGg37s3n53Em1P+usRXFuMTrX19S5UBGC/WNQ3DiAoSnph5TZMXRVSD/kBJ/oOswc72N9thuFAf7ILm/B8MiUKqfOj+ZnMdJejAzfh1S/EIo0tS+R/ZYst9x3eGWyAUlOzvCPq8W02t/pZ0HYx87WOubHBzAyMYdVnfrOlurzvqC20ZM19BREweN8MC73zGD7ynufDpeIiIiIiIg+Gt5n4LmCiaZUuMjUXN5eCA0JQXBIGML8feDtdBGXXAKRXNCMyZ0THB/vYW2mCyVxPnB2dISTsxfCwsPg5+UJJzt7uPkmoLBuCKs8Wb2v3YnAMyYmRpvK9tvf/ja+853vaFO+ymOWyn5QtzvwnJiY0ILAjo4O7T6W7zUMkyBRpoOVINFap7YV8r2EBH3yXSX0k6C2q6tLGxFp6TXWRr6/jFaV+48aR6TKNLzSN/7Lv/yL1sZk5KbIysrSRnTKMko5aY9BQUHIzMzUpiOW97sd09re2cDzvdKv293ZOsS4O+C8kxP81bKGSP8fHIxg9ffg0FBk1o9gXaaF3JNRnup1yz0oSopCgJMdLj3sAtcgVVaVD3T1xiVHTwTFZqF1sg+VSaFwffASPIITUT8h60H2P4bP1gLPVczVRuPBSy7wyuvT74v2NzHfnQOPh87ByWQqW+OFXi3wXJ1Gc6ojLnoEo3TEOAJVvfZgS7uHYmqAHzztL+Kikyc81X5Pvx+7BDtXH4SlFaNlakcbAaX/HhJ4LqC/Ig4O6jMdfX30+z9ZfvVnqH8AvOwdtO/o4qveK0S/rMGh6u8B7nA9/29wj72MnhVj4DmFppwQPPxv5xCS14xpw1S2+vqWAOkEO2O1SPF+AM5x5ehfuWYIPEdQleSPc+cuwD3AXwveg0NCEertDGcHB7h4xaCkYxJrMopw/xDHW/24HOGGBzwz0DqxgauGwFOW58pKOzKCnfCvjslomtzE/mgRQt0exIPRVRhZ3L2x7EZqvRwcLaAh3hcO/+6OrK4ZbByd4Gi9F3lhXrCPKMfo0hZkquPTNjNXj1gP1WYiqzGzYinw7EamuzPsfQowsGISeE5UINTZEfaJzVi5ZeCpyHdS9aab70BepDq+cFTr084NbsEhCAkKhL+LWp/OngiMTUf5wLr2Pjfalrx2G2uTTciMDIKPnTqGueAOd1WnYYFB8FXt4qKjN6LSSzG0cYwrB6uYaEyE/QVPhJWPa4GnhJpHMgXySA1iz/8rHnAJQXrbsiEs1AeeC4MViDp/EX7xdZjRAk/5bLUuD9Yx3SXTf3rC7ZL63i7e8A4LR7ifBzwc7eDg7ovInFr0zu+fTpFsSgs85bv7fRL2kYXoXlJt5KbAcww1Kd54wDkOFf0ruHarwFNtF8e7k6hPD8IluT/s6BpO3uutBlQ9Hm5PoirBGxcv+KCgcxZbMmJYfmBwNK6F0RfsE9E4uaaOISdQEu2u1lEQyvqXsC2BsSq3vz+EIn83VQcZ6JB7eG4NIz/EWW2b4ahR30Un95mVNrDTixxPF9h55mrtZXetF5n+DmqbjVXvv4kd1eYPVB3oNjqQ5uIMh4BijG1uQ7fYgRSvS7D3SkL7vNyTWLWzwx1sLjUhwc4RzqEVmNnRYXO6CbGuF+Hkn4meZWmjqv850mFtthbR5x3gHlOPxX0dVseqEeF4AS6h+Rhclx9ayGhfHZbGyxH6kCO8k1uwdrSDxf5SBNmdh0d0Kca21LqX/ufKFub6C+H/KWcEZHZh64oOs5358L1wHj4JVZjUHWvljq9uYqojG14PuCK8sB+713SYaM6Ep9r2A9IbMKtNcSzl1jHakAq3f/dATNkIDq5tY6QmGa4PXUJobhsWD/TlTq6tav2X8wPeSKqdwNH1TfSXxsLpITtEF/dg+bTcEroLI2H/ST9kNs/g+NoaOgvCYf+QExKrBrGq2p2+3ALaMkNw6cEQFHTN4+TKMloyVft52A3pDaNYN5Q7vjqD+kR/XDwXifL+hfcceO6rfmS4NAJeF+yR1DCBlT3VVtS2K/uHw61R1OYnIcTNHnYPqvMLn0AEhal+UG0z9o4e8AqMR93oMrb3NzBQkYxwHyfthzEBAUGq3w6GmzoHcZL7A8dVqPW3jV3V7+yrfmRnqwOXfc7j/EPeKBhaxbb6/vKjD9mf7Sx1ozAxEgGOl073ZyGyP1Pb7SX1mUExuehe3MLGdCuyw/3gprZhOzdVJiQI/gGqzdo5ITAuGRUDa9qPjLZXx9T2FgwvV9XPObircqEI9POD8yU7uHhHIrWgA/OnP+LZx9HRFuYHihBs54Oo4gFsqvqRepR7/W5MdyHH+1NwDclG15q+nizVqe3bV+cUU6hNCoKLR7r2w54D1U/dvwEvERERERERfRDvI/Dcx+HeujrhrkF6TAxiY2O1AEATFY+45GJUdk5gafvYcLItv8Teg25jCl0NBUhNi1blohGVEI/Ushr0zqxq9xBi2Hl/uxOBp5B7dhrbX3x8vMUyH8btDDxlW5LQT6Z9lTDt3aayNSXlJHST10rQZqmMtZDvKiSY7evr04JPCXrf67Lea9JWZSSuBFUyYlPCWxlh6+XlpU1pK6NzjfdclT9lncrIVWOwKf8Wsn6t/R6e748hvFruRWl6MuKi1XZn2v/HqL49Nh45LdPY0Kl+3xBOaeHVwQom6wqRHx+LWEP52Pg8FNT2YHpjFbr1AVSo7Tc+oRANvavaxWWz6TYllNrZwHJPCWISU5HVOGHYF21hZbQO6QnpyJWpbE2DLPns/UPsbSxisDoFCRn5aJ/RX7jWv+ceJAzcmx5Hb3k60jMMyyH7sZQSVHVOYmVHpvQ0abd78oOfVUx2lSNF7cfMl19R/45VbSZeiYs1eVx7LgZREQnIr+7G7I4EPOq9dhcwUJeLqORStJkGkQYS2O7M9qAqKwqp5R2YXD/RptE82plBV1UeEiKiTL5DNKKjU5GSW4f2iTVsG4IBLSzenkRLUTqiMmsxNL+F49PgTNXByZJa/lwkBmehaXIVU/1lyIkPQX7rFJZ0xv24KQmADjHXUYjMxDDktc1gVZU7PFzXRj+5e+lDrZ1DmVbR2Gb6UJaRjPjibiyt72jr6fS91PM7ujHUpaciKbsZU+tq25LwS6ZEnu9EYWoKkioHsb4lIbrJujhLPSff62B5EWM1ecjNVm1M6iVarZOEfFxuGMDM+pEWUN78elUP8n23ZzBYmoUs47qLVusxsQhlrYOY39rQ1pl2/NNfiaT4TFzumNO3OfUee4fH0C1NoSUvFIk5ZehZvHEMdKDqe3WqEyXxCcgt78XSkUnYo7XjA+yMD6KjJBkp6hhJ7hEcHZWIhPRy1PXPYWNXtcMzIzuNpI3szg+gLjcKScUtGFtTbcS0rLTZnVn0VGUhKrUcnZPr7zCbhoyc2sNoVQL8XAJR0D6D7eP3eHwm7XmuE8WZ8QjJa8X0ss7QzmT559BxOQvxSZXoX9jC4UI78tLjEXa5E/NrO9o2Ju1gb28aLbnpSEirxYhMLzrTjMzUeESV9GJlU99utPa0M46GTNVesppUe9lSdVeH1OQExFUMYkO1E2OgvbM1ghrpL/PaMKf66K2RKiQkJiGpZhTbOtWepNz+DrbWVP+TlILUy13q2HUTa2obiElMQXqD6mfU99fCroMdbCz1qHWYjPSyfqzp1rHUfRkRCWmqz5sxfKYs6w7WZMRkbAqyqoaxvbOK2bZ8hCZkorBj/jQgl3uTLk+2IFdts3kytezuMiYasxGckI3SniVDuC1h+RYWRuqRFZWGy6pv3d9ZwFBtBgIT81E9sGII1VUbOt7ETH810iMzUNo5p63z3spUBCRdRuPImmFUtyp3so7JznKkRmWhsm8Rx7optJcmwz+lVPUbxtHfUm4NYy3FSIrKRZ3MwLI1hqbLiQhIq0LP9KZJuVUM1RUgMaYAzeNrOFkfQk1eAgIz6zA4t2Voa/L9ltBXmYuEuGJ0qH5m7/C9BFRST+vozguH5zl3ZLRNYU3CcWOfJH3biaqfzkqUJqptVfZJWl+YiazSVgwtLKr1q//xjdzjdXawCUUFieq8RfXdqlxsdg4qO0awpJ7flzaoPk/ajW57FDUpSeq75qJ1ZgM69bxxv7Knhe4rmFDLfGN/pv6U/VldN6a0H7Kp761es7s8io7KHGRr/Um0+twEXC5pxOz6hqEfkv2keu+dRQy1lSErS/qcGESr/Ufi5VK0jsxr92w93f72DtV6XcZoTSw8PIOR17tl2D+pzztWfcxEM1KcL8IrvAB92/dx4Lmv+vHlDuSEOcMjqU71FYc4Nt1PExERERERESnvPfA0kAuL2j1rFP39cIz3qTk03GfrTHntgoOxnCKvOdT/Wp+/yr3/3anAUyQlJWksPfdh3c7AU8j29E7b1Tv5MK+92+Q7SuAn9x+VsFPCWkvlrJGsZxmx+c///M/w9fXVwk+5j+UDDzygBaAyRalxHcifxr8bw807sX6sI/A0UH25dl9EYz9uZPi3NiXgTa9Rbdd4nzON4TVyrzypL8N7ytSoFl9vIPsd7TNNQittilV5P4tBltB/ttzXzNIFYAnXzPZN77Af01Pr/ODs/s/gdPmM73Pzc7LMN/Z56rsdGL6b2hfe/FmKVjc3v06+s/Gz9J9h/ExL+1VDeeP0h5aeU6/VRsfKvl0+T5bfrJw5Yx2c3i9VrYfZxgQEurgjqXEKqzuqDo3Bm7HNGEYjnX0vCUQOtGU4E4JIoCGP3zKgs0B9ltbWpD5O60SmS7W07OZOj1OkXk3qU0Jm07BVf/xjoa3K67XPvbmt6Uf/yXq0XAdSf++vHZowfK5+e7LwvLQzbf1b3gZM7R9ewVp/MeI87RGa34Fp3a3D1psY1/NN7czY/mQ6WvNy5sumypm+XsJa+be0fbNyJu3FrNzZujX0K8Z2JX2F/PtsOcP3Od3GtG1A/ftsnyLlZL0YXm+pPxL6da0vJ8sk24qsz7PtRcrd6LveoZyhj9M/buwz1L/P9Bnm7fLWfYt+2zW+3qRtmJWT1+vL6R+/sQ4tlzM+rt+GTte1aTl5XMq9533knqrDRbSkB8LNOQG1Y8vYuWkkn/7zpY/Uthvjdivbwk3f09CfnJaVurK0fRnalyz7Tc8p77Y/M5Qz608UKaNNk392+VU5rQ5Nvpf+/Mi8ne6p99pZHkNNnCtcQ1PRNq/vs2XZZJr25eEqxDi7IDSzA0v38YhHuX/ncnsuwjwcEV3ej8WdK+D9O4mIiIiIiOis9x14Er0fchHnTgWed9LtDjw/aqT/sLV+RNpqf38/XFxctHvCStgpoz2lX5TH78U9VK0q8CSyQJticqMPOcHu8E5qxPTaLg5PR5KSzdg7wJX9adSm+MM1KA8dMzqcHL+PwJnodjk4xu5MDRIDfRBR1IOFrYObQt6Pjj0cHu1ieawWsR6eiCgcxPZpkH+EI908eksi4BWQjLpJHY7u23qS6WxX0JETCjefVDSOreGQ09kSERERERGRBQw86Y5i4Em2Qvo8mapWgsSMjAytDcj6l3tyyuMMPIkskB83HGxg6HI4XN3CUTqwiO39s6O8yPrt4eBkD3NNGfB38UJS7bD+XrBcj3RXqXa4u4rWzCB4hRWga24bB0fmIx4/SmT07sHWHLoKQ+DqHo2ysa3Tkbzy59JALRL8fBBXOYndk/s3ANxTfZFuqhZJ3i7wy2jG5MYBzKadJyIiIiIiIjJg4El3FANPsjUHBwda/2ecqlb+vF335Hy/GHiS9ZOpbfdxONeO/MwEFLbPYU13qI4jLJUlq7Z/iCtrw6gpSEBaVR9mNo5vTE9MdDdoI8aHUJNbiKLWOazo7uN7Ur4HMuXt9vIUWnITkFXUhYXT6ZxVPe2tYrq7CllZDehZOrqvp3fdPzzGYm8ZchKy0DC6BN2Jyf2QiYiIiIiIiEww8KQ7ioEn2SLp/6yhD2TgSTZDu9+g3ANUbTuWnifbIEGK3FPwFvccJbrzpA3K/SzZBjXqWER/j+CzIzj193/V7t/8EQiF9feqlR9h8PyUiIiIiIiIbo2BJ91RDDyJPjgGnkRERERERERERERE746BJ91RDDyJPjgGnkRERERERERERERE7+6mwDMiIgLXrl3TQh65mE70YTz22GOYnJy0ycDT3d0dNTU1+MxnPmNx2YjutE9/+tPIyMiAn58fA08iIiIiIiIiIiIiolswCzwl7PTx8UFXV5d2Mb2jo4PoQ+np6UFpaSlcXFxsLvD08vLS/t7X12dx2YjuNGl7Muo+MDCQgScRERERERERERER0S2cBp4SRsXHx2shj1xMJ7qdgoKCbCrwlFBJRjy7ublpYa2lZSK6G2Rq5ejo6NPth4EnEREREREREREREZG508DTNOghuhPOtjVrJwGTpeUguttMfywg/2bgSURERERERERERER0w02BJxERWS8GnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RAGnkRERERERERERERE5hh4EhHZEAaeRERERERERERERETmGHgSEdkQBp5EREREREREREREROYYeBIR2RBj4NnT04NHH30UR0dHREREREREREREREQfaQw8iYhsiDHwrKmpwfLyMmZmZoiIiIiIiIiIiIiIPtIYeBIR2RAJPP39/bXQ093dnYiIiIiIiIiIiIjoI4+BJxGRDUpKSkJiYiIRERERERERERER0UceA08iIiIiIiIiIiIiIiIislkMPImIiIiIiIiIiIiIiIjIZjHwJCIiIiIiIiIiIiIiIiKbxcCTiIiIiIiIiIiIiIiIiGwWA08iIiIiIiIiIiIiIiIislkMPImIiIiIiIiIiIiIiIjIZjHwJCIiIiIiIiIiIiIiIiKbxcCTiIiIiIiIiIiIiIiIiGwWA08iIiIiIiIiIiIiIiIislkMPImIiIiIiIiIiIiIiIjIZjHwJCIiIiIiIiIiIiIiIiKbxcCTiIiIiIiIiIiIiIiIiGzWx2JiYnC/iI6ORmxsLJKSkiwurDVITEy06u93PzPWfXp6OhHdR1JTU5GQkGBxu6e7S9YD93H3nuzvhKXn6O6RbYHrgYjeCY9f7h2el9873D/eW+x37h32O/cO+517i/3OvcN+595hv3PvfKyhoQH3i+bmZlRVVSEjI8NqN+bc3FztAj07m7tL6lvqPi0tDYGBgQgJCSGi+0BwcLD2Y5fCwkKL2z7dXcZ+lvu4e0fqPisrS8P1cO9I3cvxnmwTlp4nIpIfbEkfkZKSYvF5unOkj87JyeF5+T0g9S3Xa6T+Wfd3n/Q3eXl57HfuAWO/Y83XK+9X7HfuLfY79w77nXuH/c699bGnn34a94OnnnoKr7/+Or75zW+ioqICcXFxFhf4XpJUv7+/H0VFRfx1y10mI3/7+vpw+fJl/Nmf/Rn+/u//nojuA3/1V38FOzs7zM3Nads6DyTuDWO9DwwMID8/n/u4eyg+Ph4tLS1obGzU/m6pDN15sg3I8Z4c9/FXnUR0lvQL8sOUwcFB/lDoHpA+uqenB2VlZdxX3mVS3/Ij9c7OTtb9XSb9TmZmJoaGhhj23wPS73R3d6O8vJxt/y6T+q6srERXVxfr/i6TfkZCH+l3GLrdfdLepd+R9s+2f3dJfUs+JfXPur+7pJ/52BNPPIH7we9+9zu8/PLL+NrXvqYdQFhz4CmhGy8G310SeMpJrYwC+8u//Ev80z/9ExHdB/72b/8W9vb2mJ2d1bZ1HkDfG8Z6Z+B578nxjzHwtMZjoY8K2QbkeI+BJxFZYgw85QIgA8+7j4HnvSP1zcDz3mDgeW8x8Lx3pL4ZeN4b0s8w8Lx3pL1LvyPBG9v+3SX1zcDz3pB+5mMSFN4Pfvvb3+Kll17CV7/6VasKPOWgxtihywGm/IqXIzzvPgk8e3t7GXgS3WcYeFoHY73LPq6goID7uHtIjn9aW1vR1NTEwPMekm1Ajvdkm2DgSURnGQPPkZERBp73gPTRcm7I4OHuk/qurq5m8HAPGANP6XcYeN590t6l32HwcPdJfcsPLeSHLqz7u8u032HgefdJe5d2zxGed5/Ut9Q7+527T/oZBp53kJxISYcuJ7Hyb+no5VctDDzvPgaeRPcnBp7WwVjvciLDwPPekuOftrY27b7mDDzvHWPgKcd9DDyJ6CzpF7KzszE6OsrA8x6QPlpG4DN4uPukvmtqangB8B4wBg/S7zDwvPukvcttlhg83H1S3/JDC7kmyLq/u0z7HQaed5+x35HAn23/7pL6lnqX+mfd313SzzDwvEPkJEpOXpeWlk4PaKSjl4vBxcXFvBh8lxkDT5lejoEn0f3jb/7mb7TAk/fwvLeM9S4nMvLDEu7j7h05/mlvb9emtWXgee/INiDHe3Lcx8CTiM4yBp5jY2MMHu4BOTeXafgZeN59cmxSW1vL4OEekH5HRpZLv8Pg4e4z9jsMPO8+6XfkhxYMHu4+Y+Bp7Hd4XnR3SXuXH3hJ4M+2f3dJfUvgKfXPur+7pJ9h4HkHyEWu1NRU7QL8888/r92fIioqSqtwuRhcUlLCi8F3GQNPovsTA0/rYKx3OZFh4HlvyfGPHHfItLYMPO8d2QbkeE+O+3hiT0RnSb8ggefk5CQDz3tALjzJlOMMHu4+OTapq6vTLgDyOOXukn5HAk/pdxh43n3Gfocjre4+6WvkhxYSOLPu7y7pdyTwNPY7PC+6u4z9jgT+3OfeXVL3EjRL/bPfubukn2HgeZsZw06ZXvGpp57CW2+9pU0rZww85WKwXABjY7+7JPCUX3PJ9HIMPInuH8bAc35+XtvWeeJ+bxjrXU5k5IclDDzvHTn+kftiybS2PKm5d+Q4T4735LiPJ/ZEdJb0CxJ4Tk1NMfC8B6SPlhH4DB7uPjk2qa+v14IHHqfcXdLvSOA5PT3NwPMekL5meHhYuwDOtn93SX3LDy0keGDd313S70jgKf2O/MnzortL+h25xQoDz7tP6lvqXeqfx5p3l/QzDDxvI7nAm5KSgpmZGTz55JN47bXXNKaBp1wMLi0ttb3Grg6GE2KjEBkZhZg429tBMfC8330cH/+nf8Df/+1/w5/92Z+d8ef4q7/9O/zjxz9u4XVk6+6PwDMJifGxiImKVH2sKdXfxicgSe1XLL/OehjrXS7c2k7gmYSkhFhEmdW5UTSio2MRn2B77Un2d93d3dq0tvJ3S2WsVlK8he3AICoWCTa0fctxnhzvyXEfT+w/2pKS4hBjqU2LqBjEJ1l+Hd3fpF/IycnRLgDaYuCZlBiP2Bh1bnimz46OiUVcotq/WniNNZE+Wkbg20rwkJQYi+ioKETf8jxc1XlcDKKiolX9W3reekh9NzQ02GzwkJKo+nTV7qNiE5CYZP3H6Kak35HAU65X2eZIqxSkJCUiXut71P4zUf3bYjnrJP2O/NDCpoIH7dhc9T2xiTf360kJiJV9gI30OxJ4SvBgS/1OitrXav1NTLzN9TdGpv2ONQeeKdo1mRj98Ux0jGrT71zfKcmJSIiL1spHxcQhQfVPlsrda9LvyA8tZISz1bd9tX+NNhxPxsTf6rhYsolomznekXqX+relDCgpMQFxMaqODetCa+OqvmPiEtT5iuXXWBvpZxh43ibGkZ3GsPPVV1/Fiy++eFPgKSe1Nhd4qoPKJLVsuVWdGOjtQkNRqurMrf9E1hQDz/vcP/4D/v6f/if+3c4f8cmpSMvKQU52FrLS05CaEAW3hz6B//Mv/hr/wNDzviOBp4ODg20GnikpSIqPRWRMAtIKqlDf1Y/+4RHtRHh4eAgDfd1ovFyADLV/sfb+1ljvsg+Uftb6A091QpOchszCWnT292NwaES78CmGhwYwONiO1sYK5KfHq/UTq/Z5lt7DOsn+TqZwl2ltbSrwVG0oKbMUjR09GBgcwohhfZzqbcDlzDR1ImQb27gc58nxnhz32d4FRbo9VJtOTEF6ZhmazvQzRkN9rSjPUuUYen7kSL8ggadMyW87gWeK/gK3XAhMykF5bTt6+4cxPDKKEXXc0tffh9aachSnJSLFyi9CSR89Pj5uA4Gn9A8pSMutQlt3N9qqcpGacqbPkP1nijqmKWtCT1czKrJlPVlve5L6bmxs1C4AWv3F17OSEpGQU6aOVfrRVXcZ2WkSelooZ6Wk35GR5dLv2GTgKfWflovihm70d9SjJNu26l/6HZn5wyaCB0X6mdS0YjSovqe1Kg9pJn2PXBCPj09HefsAhoZ7UJuXqu+LzryHtZD6lh9ayLGXzfQ70t6zS9Eg/U19EXJsrL8xkn5GAk/pd6w28FRtNyE5A3mljeq4ph89bfUozop9h/pOQnxiJvLLGrXp2TsbK1CQap3rR9q79DsS+Ftv29cf66TkVKC1p0/VqepT8hORmHzmhxaG45286nb0dLeiMicVKVbe70i920y/k6L2UzFRiEvOQnFtk9oWBtUx/og6xh9Gb28bqkuzkRgbi5h4tQ2rshbfw0pIP3NbA8/f/u63ePL3T+KlZ57XPPfUM9pj4imTx581PG7pPT6oexl4WhrZ+cILL1gMPGWq27KyMpsKPBPjEtRJVhNWfgz13+v4zaPdyFUN3JZ2tgw873N//9f48487IKrzS9JI8fYzqt956gU8/yftn/j+/iDiLvwL/v6v/8Hy68lm2WzgqfYZMmo+OTMblYPL2P/KL/Gcaq9vvvkqXlX7jbffkpb7On6wMYqysEjEWnoPK2KsdzmRsYnAMykesUl5qBr/El5RNf3HN17Bs88+i+dfehFvSNWr/7/y6i/wxaM5tFWVICNKnfBYeh8rZNzfybS2thN4qhMVdYyUWL6G770k9f8mXnxBHUc+95zm+efVnz87RFtRFpLkl4UW38O6yHGeHO/JcZ/NXVCk2yQR8bFpKKzchhxC/0n178Y2rW/Xz+N3P/48pi+rtm8DI+Lo9pJ+QQLPhYUFGwk8U7Rf3ickpiC3rAfTm5/DT36nDlZeeR2vv/Y8Xn5T+m7gD0/+FF+caECZlLXic0Xpo2UEvtWPtJIL3olpyO14BE++/TaeuNaGrDR5zKS9JMYjLjUP5ds/xB9f/wUOGtPVYxZGY1kJqe+mpibbCh6M4mMQ0byNH6hjlde/NI6GvAjExFsoZ6Wk35HAc3Fx0TYDz/hohBW0YeFbbwPPfRMr9eGItqH6l/Y+MTFh5cGDURIS4lOQWbCIb7/5Jn73aCdyDX2PjPCPi01F9eAufqB2Ay/+9NOYLk/V+h1rvUYo9S0/tJDgx2b6HdXfhDeu4zvPqzPTr8+gOT/cpvobI+lnJPCUfsdqA091zBKZVIrOje/pD2Ze+jEOuxMRHnuLY7OEKERm1GHqsaf1xb93hP6sCMRa4Y+9pL3LD7xkKnmrbfvasU4qMpoO8BvDNdxfPtKB0uR4JJjMuCV9T2J6Hroefxp/fOu3uNKSidRE6/0hgNS31LvUv9X3OxJ2Rscjq6gag5vX8d1n5KLMG3jjpdfw2htvy9/wxA8ew/JEE3JTk5EQZ93X+6Sfua2Bp4Sd3//5j7Dz5evQffkavvD9r2sB55NP/B7f/dkP1ePX1ONX8eUffFN7/HaGnvcq8Dw7stMYdt4q8JSLwfL9bCfwTEBcfBaK2o/x07dews9/9Cu8/NxXMZuvOhobujgjF33llzfFxcUMPO9Hf//X+IuP2yGq6yt4/ulvY6vADZ6havus6cPc9S/gt2/+Ab+80gbf//GX+Nt/sPB6slnGwFMuGMq2bisjJJLiopGYloP+w8/jmTeB1379PXz9kQOszQxgcHgYczPbuPblfayMt6BApvK0+D7Ww1jvsh6kn7WNwDMXleNfwLNvvoTvXplAgzoYbe3sxOSGDrq9T+Nz3/0JnpY09NdfxXJlLhJibGGa3hv7O5nW1vYCzxV865nX8ex3DzHU1Yz6hibtGKqlpRnNLSVIz0i1mR81yHGeHO/JcZ/NXVCk28QQeFZt4Xt/eBk/fGQGzU2NaGxS7VnadWsrGmrqUCDH0zbSrun2kX4hNzcXS0tLNhF4yjSeUfGJyGtdxRd/+Sr+9MIv8Z3P/gdO5scwNtyC3qll7F/5Kr77y6fw0y/r0JMTaZUX/oykj5Zp+K1+pJUh8MxpO8GvXnkFvzhquUXgmYuy9W/j1ed/iJ166w485dhE+kCbCh6MZLrDxnV86yng+c+NoC5Xpt2zUM5KSb8jgaf0OzZ5L734aITnt2D2K+oA/YkvY6E2wuYCT/mhhU0Fnvlz+OpLL+HnV9qRo/qeeLUfiItORXHnjjq2AZ793hUMF8Rpj1vzgAipbwk8JXC2mX5HfmBRv4yv/R548YuTaLSxH1gYST8jgadV9ztyjJNUgvbVb+Jldfr/p7efxo9PhpAeG21hX5qEuIhY5DTN4fEnpPCbeOqb++jNss7jHmO/IyOcrbbtGwPPhh385JW38aYWev4cxw25SFLHa8Yf0OkDz1x0XPsNXn35Zzhosv7AU+pd6t+6+x25PhmJpKwGbHzzGVX3L+N3P/kSjk8WMNk1hKGJeeycfA7f/dkL6rmn8OWNTmSrdRFjxbd/kn7mtgaeLz3zAna/+gj+Z1sI/qUtFJGz5Vq4+dpzL2Hjiyf4v1uDtcfj5qvwtR99Wxv1ael9Poh7EXi+U9h5q8BTLgbbVOCZoA5esorQde0neO7HVzDUcYKfv/AMvjqXh7gEdSJlxQc1phh43ucMgWd099fw1G8/jfbA/4w/+8u/xl//H/8b/ssD/qj59FvAbx5DZ8h/wV/8jYXXk82yycAzKQGRCWloXfsKnnzrdTz5lR0MFGYgLkydtMfGafuv2NgYREfFINbG7uEpJzLSz1r9Pu408PwSnn/9KXx9sVjbT8TFyS+Wpe7DEBWbhubpz+C3f/gTXvnJCbrz1cmNlU/RJ2Q55L5YPT092t8tlbE+5oHnc18YRklWHCKj5QJKvIHtHHMI+c5yvCd9k81dUKTbxBB4Vm/j+689h++sVSAhLhaxqp8xtms5l7DWUILuLOkXJPBcWVnRAk/r7idUW45LQlrDHB79xWv4w5NfwHprLhJCI9S+Uo5bVHuW+1iFxyO7pBldfS2oyLlxgcoayfYn5/BWHzzcp4FnS0uLFjzYznGKwX0SeEq/w8Dz7pO+Rm51YNUjrU7dHHhmp8YjJiYWl9t28B9qG3j5Z1cwclntA9T5qrXP/iZ9jYwst/7gwcR9FnhKvyN/WmW/Ywg8O9R+9Nk/vI5nn3oSLz35VazXpiDybKiTGIPohEqM7P8AT+FNvPryc3j62wdWHXjKD7wk8Lfatn8aeO7hRy++hqd++W08+cof8dw3llGXrY4xDedLthp4Sv1bdb+j6j8qORvDV3+Kl996Dr98ZAhlmVEICY9R/bsc58ciOiIUifmdOP7WC/jjaz/G7lAZkhOirbbupZ/5QIHn73//e83ZxyXw3PnKdS3UdBxMxSfaw1Gw0Qn8AdiTILQ1WHv8f7WHoVzXr/aQb9626W3vduBpDDtlqjJLYeetAk8Zxl9RUaGdZFl6X2uTEBuPzMIOXP/Fy/jxdh3Si9px9ItX8eI31lCaLh2LDYQLihzgSOBZUlLCwPN+ZBp4/u6z6Ar5c/zV3/0j/vGv/iv+8yd8cPnKy8CvrqLB47/iL//OwuvJZhkDT+lbZVu3hcAzKTYMsbXTeOwJ4I2fHGOwIBoh0bZ90dtY78vLy1o/a/X7OLPA82l8Y7lc20ebBmpJ8dGISS1C9+ETePtPz+F72/U2MZ2q7O+Ghoa0+3jazoXEM4HnF8dQnpuE2HjbOMawRLYBOd6TvskqT+zpLkg0Czy/u1GNFHVCae0XBenukH5BAs+1tTXrn1oyIRpRmfWY/MzT6sDlRzjuyUVQRJyF/WESEhMkzLf+i99yrUDO460+eLiPA08JHmznOMXgPgg8ZSpt6XcYeN590tfIDy2seqTVqTOB50kr0uMjkVozhM+qc9jXf/UdrDQlaEGELRzXSF8j12UlcLb+uje4jwJP+aGF9DtWH3hufg8vPv0LfO+zj+Nnf3wVPz7qQVJ4rNn+NCEqEpkN0/jcb1/A07/6Pr7xy5fx/HetO/CUfkcCf6vd5xoDz8Z9/PTFl/Drq10Y3Pkxnv3Ty/jWSj2y5UeiMiOOjQWeUt8SNEv9W3O/kxQXjoT2HXz7JeCVryyiIVPta2Nv3k4TY8ORWLOKrz79R7zx3SW0FantJs46r9dIP/O+As8nnngCv/71r/HDH/4QP/3pT296XsLLL/7gG4ieq8C/doTjEx0RSFmqx9VvfBYrnz/U/i5h5yfUcxkrTdj/6iP4kip/O6a3vZuBp4Sdcs/Odwo7bxV4ysVgmwk8k9QBTGImKgc/i1+88nPs1cciPiUfbVs/xYuv/Qwnben6TsfSa62MdDQMPO9jxsCz5+t48jePocnj/4H/1//2v+P/+C9/gQtJLbj221fxs/0q+Pz//hv+jlPa3ldsL/BMQmx4POqmHsUTeAVfX+9AZkiU1U9Z+26M9b66unrfBJ4SVsRGJqOwdhk/eONtPPXNNVTFqoNsKz+pj4mJwfDwsLbPk79bKmN9zAPPZz/Xj7zkcASFhCMiIkITHWe9F28tMQaectxnlSf2dBck3gg8X30W31oqQmR4GMLC9W06IiISUbG2MVU23X5yPimB5/r6upUHnklIUPuSrIZJfObJN/HM1zfQlBSBOBu4wP1O5FqB3P/dtgLPl/Gz3WrER4chNOzG/jEiLATBUcnIXfyGzQSera2t2ogHq734eiv3SeAp/Q4Dz7tP+hq51YFcALf+tm8SeL74An560IC8+n7ovvcm/vTkd7DWUqiWx7YGQMgPLSR4sJl+5z4LPKXfsf7A84d47cXv4PH1UWz84A28/PMrGM6IVc8ZyiXFISI2B80rX8Izv/0GTtbmsP7jN/DS96w78JTsQnIJq237JoHnz156Bb866UBORgtWfvQC8Mq3sFyXrf9xRYLtBZ4SNEv9W++xZpJ2zatr59t4EU/i+nANUsOikWixbAKiwyqw8OXf4U+vfBVTTYWIjo63yuNN6Wfed+D5y1/+El/72tfwve99T/u36fMSWr74zPP46g+/haKtbqQtN+Bcbzz+Z2sI0pYasPnFE5Ru92rB58M9cfjnthDEzldp5T/s9LZ3K/CUC1jvNrLTyFLgKReDKysrrbix35ColjUltxpL330Or/zsAI3q+8dGJSK3bBpfe/Fl/OS4FalyAdIGTniloxkYGNAuxP/FX/yFxeCEbJjxHp7tX8CzL/wIxyN5yMvPR1lDBw6/8UP84j+GkHnxb/Cf/vqf8HFLryebZQw8ZSpV2datPvBMikVkdBXGr/wSf/rDd6HrzUeIOkiwWNaGGOtdTmTun8BT7QfjopBW3ATdT/+AF352iK7YOCRYeRuTkHNkZETb59le4LmMbz79Ol792WPYWp7B5NSMdmFC9NZkIyPFdkbHyXGeHO/JcZ9VntjTXWAIPKs28b03XsHvvrKN2ZlpTBva9Mz0OIaai7T+05bCfLo9JPDMy8vD5uamlQeeCYiJTEftyHX8/o8v4Ds7HUiONI7uTEGK/EA2JvJG+CaiohGXkIyUm97LekgfLVOOy0grq774bQw8W4/xy1dfxzPfOsDinOpHpm/sH2empzA5t4TNr/war73wQ+jqrD/wbGtr0767Vde9JfdJ4Cn9DgPPu0/6HfmhhW0FnrP48osv4VffOMS1772AV3/5NewPFyA+QT/iyvJrrY/Ut/zQQgJnm+l37rPAU/odWwg8//Dqj3HYX4Ky0U/jmTeewdc26pASGY+kFLUs0dFIKB/C8a9exnNfmkdDRTv2f/GW1Qee0u/YTuD5Kn5zrR1ZaQlIaF7HT18EXv7WCuqz5PYJcUiwscBT6l36HevNgOIRHV6PpS/9Hm8//zlM1GchLOZWP8hNQlx0GnqPfoiX3vo1DnsqkR4Va5WDN6Sfed9T2krI+fTTT2thn6XnJfSU8PKPL72BK9/4DD7ZHQ3HgRT8a3s4ire6gTdkettH8UBXlPa4jPiUEPTlZ160+H7v1d0IPOUC7nsZ2Wl0NvCUE1sZxm8bgWei6kxSkF21gG8/+zJ+tt+IRNW44+NikJRfhpmvvoTXfv44evPjbOJXXdLRMPC8jxkCz/CWx/HyW2/g1d/9Gr/69ZN49pm3gT89h6/ttSPbyxEP/MN/w//5Tx+3/B5kk2wu8ExUJy7pzVj8wrN4++kvYKk5BRExth+GGOt9Y2MDpaWl91HgGY2Uomas//Almwo8R0dHtft42lzgWbaEbzz1Gt78w2t47tln8PQzz+AZzdP4zGIp8tJV/dvAfVSFHOfJ8Z4c98nxn9X3TXQH6APPgvJ1fPePf8Trr75kaM96z/7+F/iOOjeSvsdWRkjQ7WMMPLe3t6088IxHdEQ+mqe/gpfxBL6yVIfwGMM+PjEBcRmFqGwfw+zcHOZmZzA9OY7xvlZUF6Za9cVw6aPl2NHqgwdD4JndcohfvP4W/vDay+r8xnT/qPf0M8/h+Rffxhsv/hBbtWlWH3i2t7dr11Ssuu4tuU8CT+l3GHjefdLvyKxEVj215ClD4Jk3gy/KPfWeexrA23jiP/qRGxml2r1ttR2pb/mhhQQ/NtPv3GeBp/Q7NhF4vvZzXO9LQnRRF45+B7z242P0JIUhNjEekXG5aFn+Kl5682l8broAyUX9OPqVdQee0t7lB14ywtlq2/7ZwPN6J/LS5P7AyWjb+AlexCv45ko9MmNjEJ+WY1OBp9S71L/19jsSeNZg8YtP4LlfHWOoIhGRFqazNYqPCUfj+jfxFF7C50fqkRep1omFcvea9DMfaErbH/zgBxantBXGwFPuz3kj8NTft7Noqwt4E9g/DTxT8S/q8ZLtHqsPPI1hp/wS8b2EncJS4CkXg6uqqqw+8ExSHX6C6khaNn6EZ57/AVZLwxAeFqqEICA8CTmDX8BLf3gO35jPR5xqSNY+ylM6Fwk85UI8A8/7kHGEZ9eX8dxT38R6njNcPEIQF1OG9v4DfOaHr+LN338avWGfwD/87d/jHy29B9kkCTwdHR21aSNlW7f6UCEpBpEJtZh+7Lf448vfwEZnNsKibX9KQ2O9b21t3VeBZ0JsJLLKW3H1N8Cz39ehyUYCz/Hxce0+nrY6wvPZ7+yhv70B1bX12ugbcbkkHSmpqu6t/HjDSI7z5HhPjvsYeH5U6QPPwqotfO8PL+EH1ybRUF+Hunp9m26qq0NVboHWNqw1mKA7xxh46nQ6Gwg8C9A881W8it/hyws1CDUGnhL+FNRj7Pr38dwzz+Cp515UZdR/L30XB32ZiHiHCyb3mvTRcuxo9cGD2QjP1/DLzy2gtaketXU39o8NdbWoaejE4OEvDCM8rTvwlGOTjo4O2woejO6TwHNnZ4eB5z0g/Y780MKqR1qdMgaes/jyCy/hl1/dxuGPnsAf8Gs8PtmKgmj5EaLtHNtKfUvgad3Bwxn3WeAp/Y6tBJ6PDmciIKEY3fs/xRuv/AJXR7IRGxqKmJIubP/gLbz+w2N0pnsjpnIYJ796Cy9beeApP7SQEc5W2/YtBZ4ZCer7qmOZlDZs6Id5YrkmDXEp2Wi/aluBp9S/9fY7EnjWaiM8X3vyUYyqOg57x8AzDPVr38RTbz6FRwdrkBV5n4zwfLcpbYWEnd/96Q+w8+XraD+e1qa0vdiXiICJAvRencfx1z+N5sMJbUpbedx3PA+rnz/Ec089e9N7vR93MvD8IGGnsBR4yjD+6upqKw881cFNbDwy81tx7Wng7dd/isdm5zE3O4e5+TnMTC1iY+ebeA5v4OmvziFXnfRa+y/TpXNh4HkfM97Ds/treOq3n0ZbwP8H//Uv/wZ/8zd/hv/3//NvcDFqCD/441v44XYF7P5MRnlaeA+ySTYXeKoDiqjQfPRsfVv1oL/CtfFKRIRb+4j/d2esd7lwW1ZWdp8EnkmIi4pDVsUIvvzM6/jd58aRFWcb9/CcmJjQ7uNpe4Gn/h6ez31hGCWZcYiMjtPakki0oYsqQo7z5HhPjvsYeH5UGQJPuYfna8/hO2vlSIiLRazqR4ztOsEaL/rQXWEMPHd3d21gSts01A5fwxN/ehHf3e1AUlisPkxT/VpiRhryKsrQVFeD8qYRrH/tafzh+W9hpzvzHX8hfq9JHy1TjttM4Kndw/MV/OKgAWlJsYiJvbF/jI+NRlRiJopXv2kT9/CUY5POzk7bCh6MbDzwlH5H7h0s/Y7VBg/vJD4aYXnNmP7yK8Dvv4LFOtsKPKW9r6ysWPdIq1PGKW319/D8yUELMktHcPKL1wD8Do8PVCM1KhbxNnJ8Lv2OjCyXwNlm+p37KPCUH1pIvyPBp1X2O2cDz9FchIfGIKt+Bp979lU89cUF5IeEoWTwEL986QV8Y6sBcYGhSKq2jcBTrpVJ4G+1bd9i4KnOo9Q+K14da6a0reNnknl+YxF1BTlou/obvGIjgacEzVL/1tvvJCA6vAyzn/01/vT2j7HVVYLYcMNx/k2SEBuWgp6jH+GVF7+H5fZixEcbb3NhXaSfed9T2orf//73mrOPy+jO155/GVe+8Vn8Xy2BONcTj0t9ifh4kz9aDifx+e99Df9f9XdjCPrfm/xQtTuAt154TXvt2fd7P+5U4CknER8k7BSWAk8Zxm/9gWcCYuPTkdd8jN/86TW8/Mxv8funntamMtZ7Sv3793jyhVfxxrNfx2ppmnagY60nVUI6F5nej4Hnfco08PzdZ9EV8uf4q7/7R/Xcx/F3f/Gf8AmvdGw8A/z6ehuC/utf4m8tvQfZJNsLPJMQFxmP8vGr+MWbb+Dnx4MojAlGlDp5seZ7Xb0bY73Licz9EngmxkchJjYXnRs/xMt/fAJfni5XJ5lnQ1HrIyf0U1NT2rS2Nht4fnEM5bnqgDredkNCY+Apx30MPD+q1Im6SeD53Y1qpKgTemv/0QTdHdIv5OfnY39/38oDT7U/jAlHavUQrjwBvP7TY/SnRiI0VvVrKep5CT3lglSseiyhEiNXfo23Xvy2TQSect9xqx9pdTbwPGpBVpo8ZrJPSYxHXGouyta/bTOBZ1dXlxY82M5xisF9EnhKv2ObgWcUogrbsPjN1/HH33wes+URiE6wUM5KSV8jtzqw6pFWp0wCz5dews9PWpGRovqaxlV8+VevqZ3Bd7DdV4WUmDjVjqz/GFf6GhlZLoGz9de9wX0WeEq/YzuBZx6iY6IQllKFvpOf482n/wPLHW2Y/OIL6u9fxGJlEiIiI5BiI4Gn/MBLAn+rbfu3Cjylb1HHOEmJKWjb+Cle+OOz+Pp8Azp3foSXXvgpDpqtP/CUoFnq33r7nSTERyejYu5z+O2bf8SvDgdRGheByPikM9cnU5CoHo/KGMYjv/wD8BvV5itSrfZYX/qZDxR43oqM7vzxL3+mjeA83xuPh7pj4TWag5q9IQxeX0bb0ZT2+IPdMdrIzoqdfiz+xx6ee+oZi+/3ftyJwNMYdsr9JSTgfT9hp7AUeMow/pqaGqsOPJPUcidmlmPgs7/BG89+DVsD9aitrUVtXR3qRG0NKmtaMbj2NfzhTy/jpydtSLPyi8DSuTDwvI+ZBJ5Pno7w/Gv89V/9Of7T//6f8e9xDfiC6pN/cVQPt//6l/g7S+9BNsn2Ak/pY6MQr07Wt775At5+8ft4ZLwQ6bFRCI2IUn1VHOJlBFBMNCLVv2Ni5Qb5KRbfx5pIvQs5kZF9sG0Fnk/h64vF2n5C6j82OgqRYZGIiElH/ewhfqr6jue+voqG9Bgk2EBQER0djenpaYyNjWl/t1TG+pwJPD8/jOIzIzyFLd3nUI7z5HhPjvsYeH5UMfCkWzMGnoeHh1YfeMqFwMi0QrTrvoMX33oRPzgZRmV6MmLCIhCl9p1xcfGIiwqFf1Qx+o9+hbdeso3AU0bgW/1Iq/s08Ozu7taCBwaed5cx8Dw6OrKdwDMlCYnx6hhdHdNGhIYipWocn3v2bTz7jS00Jkcjzob2qdLXyK0OrHqk1akzgeeVduSkxiFaAs7WNXz3WQCvfhubrYWIUsfr1n5sI32NjCy37uDhDJPA84UvjKE2KxgR0TfOi2T0m7X286aMgaf0OzYVeKpjm9iIVJR27+EHLz2H53/9I/zkxZfx/eNu5IbGaD/0spXAU37gJYG/1e5z3ynwVM8nyD2D09tx+JtX8NZvvozNk6/j5ed/hP2mLKsOPKW+JWiWH7pYdb+TGIPQ7A7sf/811a9/H0fDFUiIDEdYhNrHxqnj/Fh17BMWiujEAgyd/ASvvPUCvr7ehPzUSLWOLLyfFbjtgedLz7yAna9cx7+0hWojOH1Gc7Hy+UNA1dneVx/BP7eGnE5ju/WlK3jrxdfw7FPPfOjRneJ2B56yAzGGne93ZKeRpcBzb2/PygNP1anEpyKnagHfffkNPPmlCeTHx6mN0/Sio9oZRMQjp3QS33gDeOknx2hJibXqC5HSuUjgKSOPGHjeh4z38Oz+Kp75/ZcwEfd/458/cQ4Ol3wRmlqNwf/4Gd58/cfYKPbA//irv8M/WHoPsknGwFMumsi2bhOhgjpxj4uIQ17LAr74zFvAKz/D5zdn0NPZgoqKy8gpqkJVfQcGJnrRXl+KbJlG1dL7WBFj4HlwcGBjgecX8dwfnsM3t1q1C0CFRcWo6WhH5+AYVva/hJ+/8Qae/8lVTDWmIdpGRhtKyCmzUsh9PG018Hz2a0torChAdm4+CgoKDC4jKzkVKTYSHBoDTznuY+D5UcXAk27NGHgeHx/bwL30UpAYE4HU/HqsfPF3+OPbb+P36hx/abAbHVXVKL5ciLLaerQObeHRH7+qzv1/gMO+LKu+h6ecG8p9x61+pNV9Gnj29PRowYPVXny9lfsk8JR+xzYCTxlBnoHckjrUtTWg4nIbFh/9AV5+8yl8caEcSVHxNhH4GElfIz+0kMDT+tu+hcBT+h51jpeQmICisSv4ldy0+XefxmRrAaJirTd0EFLfMrJcgh+b6XcMgedXf692q19eQm95GjJzDedFhYUozMpFekqq2gas+xxD+h0JPKXfsa3AU+1HE6IQm1mL8etP4o9yj/Invoz1+gRExKu+yYYCT/mhhQT+Vtv23yXwTE5S/Ys6Fi0b/TR+9QbwwjNP4M2Xf4TdBuse4Sn1LUGz1L9VH2tKfx+VhPLuVXz9mT/ij0//CNeWJtDZ3oCSkgoUVzegc2QIq1e/j1dffRO/+Y8FVOamaD9stNZZ6u5Y4CnT2f735gAUbHRq09W+9MzzWP/iMf6Heuy/N/ujbLsPb7/44aexNXU7A8/bEXYKS4GnXAyW0ZJWG3iqE6b4tHw0bv0cb+MFfGWyEEkWLs4kJsQgKacEE//xkur1n8GXx0tVB2W9J1bSuTDwvI/9/V/hzz/ugJi+b6r2+Dae/co1XL32eXz9a0/jLfXI609+G/s9KXD9+J/hb/7/7J0FWBtLF4apG/WWuru7u7u7G9Td3d3d3Z06Fdzd3d2dun3/mU1SAgRKaS+b9p/vPt9zy85kk+yenDmz70qtOorXwf1X+q8EnuRZGtMxSX0e1h24DWO3MHxkgfrlLfz9XWDjFoSgqLe0IBSWT09ixdhJmK5gHcpkGfBkZ26uX79eiU/qkVoAnkuw8YINPtCWfhfpB3t7ezi7uyP040d8/voZH2NpmfkNHNk+GxOnzFC8HiU0g5ysfmHP8fzrgOf6+/BgB08+RMHD1QkODo5wdCQ7OdH/zXF98zLMpzpF2U8AYGa/AVbvsbqPA8//V0uA54otz+GPT/B9vIUDT+4flgHP169f/wXAk8xO1po8AwuX7sBdLQsERSZQsv6KpOAQuLs4wyc0Fl/ff0ZSdAAcX9/DkU1zlPq25GxuyJ47rvTgQQo8Fx/Qoxk3EKGzDwsVAs8lWP/IC/gcCK0dyg88jxw5Ilzx8NeAB5mnT8aEXY/gSWX6Z+vz2L7k73qGJMs77NnBLO/8HcBzGiZPWIFdl0zg9T4W4f5sfvQO/jrXsHPJeKWECxmZ5R32qAN2xY/yx74UeC67BZdv3xBucBCLpblHg9Xi5F23tRH0mXZJjA0u71sm5Ctlvesb297synIGHv6avEP5ZvyO+3CKo22cFAZ/Z1vYyeZGzs5wfnUbO1ctwpRpyj1PZXmHAU+Wd5QZeE7UWINDTwNpY4fD9MJSTJrGPqc6poybifVHXiDsKxBpfh3rNCZhOsW5+tQJmLXlHPRocP7u9wbHF05QWuDJTvD6K4DnrtcI+wbEGh/GUnngSdaYzuZQq3DaIIz2EVMYXu6cp/TAk213dqKLcgNP8iwW6zOw9vBV6LiF4yM7SPYlCl5e/nAPjqGRl/5MCoL161vYsnA+ZkyZJnm0haJ1KYH/OPBkV2uau9kJt6pd9+gYrho/RkxElLDc2MVaWLbu0VHcNH0mLFO0jqz6TwHPPwU7mRUBT3bbInZbWGU9GKxByWLmvMXYfvUV9GmyengZJRh2IDtNX3VMU5+HRVsuQsdYFy8vb6ckIzngnbKfcpglmpMnTwqxwYHnP+ia1VClThv0nroN1+8/xKNnL+i39hzPnj3GgxvnsUW9D9rWLYOKNeqgjqLXc/+1lgFPdpY4+63/TVBh1swZmDJhBuYu24lzN1/CwMAMlpZWsLaygIW5AYyMbuHo7jWYNUX5z16WAc9Xr179JcCTCmiN+Vi2/RJeGRvD1NwSVlZWgi1MTWGoeR+n9q7CrNmTaBL598QUM4Oc165dw4ULF/4u4MliaOkB3NLShYmpOSyl++OHLbVxZfsSzGNneP4FwIj9Bli9x+o+Vv/9TbmJ+0+Z3YZvNhatOIZ7uq9w98gK4QplZX8OMHf2mOUFdpWGtrb23wE8mWfR554+GVMna2DLrhO4r6cHXQsLIUdbGhnD+MltXDmwFQtm0Fg0XXnP+mZmB57YLceVH3hSHtGYjfnrz+CJjg4en16HubPZMrkxhR0onDUfSw/fge7r+zi+enY683flMNveR48e/bvAg8zq0zF1zWHc1jLG68s7sGr+VKW9nZsiy4Anyzt/B/BUx7QpC7B2xyW8NDOHhaUZ9DTPYufimZhI9bky5xhFlp1oodS3lvxhyjPqszB3wT7coHh5dGYD5svlHvUZ0ymeZmHnDSMYm5hA68wazJklqefTrkt8s+3Nrixn4OevyTuUb6asPojrT3RhzOLfyjp5XsT8+jK2r5n/VwBPdmU5yzsMfCpl3qH5JTsZesOR+9DTfYTzOxZg2gxprE+bjHlrd+HaAy3c2L8cEwQQygDcVMxasR1nnhhA+95JbJ5L44ES1vgs3tmJFuwKZ6WNfaHWmYU5a05CU1sXT89txII5qWoddhIGjbezaF712NAYhnqPcGL1HOFkUmU+0YJtd7b9/4q8w05unDQWMxbtwtnrT2FiYgRLS0tYWphDV+cJLh3diLkaUzGJ5Rwlhp3MLM/8UeDJrthkz/FMiokXHBsZIyxLu/zP3MZW3n8CeLINwhIxK77fvmVnjwGfP3/Gly9fsuSvX78K62ATqYkTJwqJnl3Gzw6AKTXdp6QyY8pETGDPk8uwgKcExM5yHD9B6a9+YcmFA89/2Qxk1kT1KuWhVro0SstZTa0Myleqiuo1+ZWd/6L/ZuApMeXRGdMwZTLLueMxfrzMEyi3TsbU6ayY+Hue4cnO3NywYYPyA0/BbAybgok/tnmyJ0xioHMGNP6yM8eZGeS8fv06Ll68+BcBT6nVp2HyxAlp9ofEEzGFJp7KDv9lZnUeq/dY3ceB5/+3NdRpYjhhonBrLEXt3P+flgFPHR2dvwd4/rCG8LzxSRNYrSLN0ezfNHZOnvp3PG+Z5Wh2y/G/40oryiMzJNub3TZS8ThINc00mpdP/Nn8XXyz2uTYsWPCFQ9/xQHAFJ6FWUKtMh4Tp7BYp78V9lNOy4AnyztKe6VVKs8SnuGZXK9PmDQF09T/PtjJzPLOkydPlPtKq9TWYFfZppN7KNdPmyzJ/5OU+BbmzGx7syvL/xrwIFiabyalMzeaOEW4Am6WkoMHGfDU1dVVXuBJnkXj6Ixpk4Tj4FOmy+WYWbNoDJ5O+0FSyydv71mSk2Bo/0yYNBUzaDyQX5+ymMU7O9GCXeGs9LEvzJkkfCG9OT+rhyay42Y/5RXim21vBjzZ9v+b8o4G5R12fJLldlm+mcDmskKNr+g1yuc/DjzF9J8AniwRr169WhgE9fX1hStVfsfswC8rJtltVFlxw9bPlm3btk25gec/aJZcOPDk5v73zIBnr169hNtisd86hwriWAY82Zmbfw/w/DfN7ihx48YNXLp0Sfi3oj7c/71ZncfqPVb3sfqP5yZubm55s7zAgKeent5fCDz/frMc/ezZs7/kSqt/yzLgyY65/HUnZv3lZnmHAU+Wd/4W4PkvmeUddqLFXwU8/xGzXMOuLGdX9vNtn71meYcBT5Z3GPBkfyvqx/3fmMU7O9GCXeHMYz97zbY3A81s+/Ntn71meYYDz1RmRR8bDCdMmPDHLEvo7P9v3rzhwFMET54yGRfOnsO29ZtRrqQaaletwc3N/Q+4StmK6NutF55pPhF+6xwqiGMZ8GRnbm7cuJEDTxHNIOfNmzdx+fJlDjxFtAx4srqP1X88N3Fzc8ub5QUGPA0MDDjwFMEsR7NbjnPwkP1mx1qOHz8uXPHAgWf2muUd9uxglnc48Mx+s1zDTrRQ6ltL/qNmuYadaMHBQ/ab5R0GPFne4cAz+83inZ1owa5w5mNu9pptewaa2fbneSd7zfLMPwk816xZIxzkY8/jlJkdfE3PbMKTkVlgZmSWNDIy+yzslrbsMmB2Vgs7AMZAqPzn4/5vPXXSFCzftg6j1migUpeGqNm7BTc39z/gqt2aoNW4Xlh1bJvk9045PfXvn/u/t2w8NTIyEp7hmXoM5s4+jx07VrjFM3uOJ/u3oj7c/71ZncduacvuGMJqRfb7UNSPm5v7/9MsL7ArrUxNTTF79mxhzqmoH/d/Y5aj2RX4DHiyObqiPtz/jceNG4cTJ04IBwDZvxX14f5vzPIOAw4s78ybN4/nnWw2yzXsUQfsih+ed7LXLNcw4MlOdOHbPnvN8g57ZjDLO+wEL/a3on7c/41ZvGtpaQlXOPMxN3vNtjcDzWz787yTvWZ55p8Dnuzhzbt37xZuqbd582Zs2bJFOODEICPz9u3bsWPHDuzcuRO7du0SzPrv2bNHeNYmM3uWB7u9DZsAsbOvmFlRwsg8C1ZmlizYgMnOTmQFOzO7ZeqpU6dw+vRpnDlzRvDZs2dx7tw5wefPnxcCnb0/O8OFndXLnT3esHwNui8YhRyzm6DYog4ourA9Nzf3P+L881uhwuzOWLF8BZYvW64wB3Bnj9mthdlYy8c48czO2Gf1BqtB2L8V9eH+781+A6zWZPCZQQ1Ffbi5uf9/zfICO0Ho/v37WLVqlXDVlaJ+3P+NWY5mt39nc34GgBT14f5vzGoTdjzl6tWrvE7JZrO8wx63xJ6fyh7lxPNO9prlGpZ32HFGHvvZa7a92THd69ev822fzZbPO+ziJD4vyl6zvMPinnENHvvZa7a92XZn25/Xmtlrlmf+OeBpaWkpFBDsIJMMYqYGmPLwMjW4TA0tZcCSHTy8cOECLl68KDwXi90q7sqVK0Khzq6iYAHMihd2G7nbt28LB7iY7927J0xkWXJ/+PChsE72jDMLCwvubLSdlQ0uPr2NhVd2YLPmCW5u7n/Iq+8cxMbrh2BpYanw98+dfWa3CTI0NFTYxp19ZmePs2eJK2rjzj6zWzexK1gUtXFzc3ObmJgIzxMzMzNT2M7935rdWpLdfUlRG/d/ax0dHeFKK0Vt3P+ted4R1yzvsEeAKGrj/m/N8s7z588VtnH/t2ZXd7K8w/6vqJ37vzWLexb/itq4/1uzfM/zjjjmt7Qly9++VpHZpbAZWdFtbOXNPgszu4SZXU3KPidX9ispPgFvYxKkf3Fxcf1LCg8Klf6LS0z5+/vj69ev0r+4xFJUVBRiYmKkf3GJpc+fPyMgIED6FxcXF1da+fn5Sf/Fld1ixw/ev38v/YsrO5WUlISwsDDpX1zZLZ53xBPPO+Lp7du3wrFjLnHE8454YnmHxT9X9uvdu3c874ikfxJ4rlu3TgCZih5cKqbZQ1PZFafsQCRX9is8PBzBwcHSv7i4uP4VsSLCy8tL+heXmGL7ge0PLnHFaiJ+IFF8sQO63t7e0r+4uLi4UurTp0/w9PTkJwqJJHbwNS4uTvoXV3YqOjqanxAkktjJWDzviCeed8QTOxmUnZzLlf368uWLkHfY/7myXyzv8JOhxVFsbCzPOyKJA89sNAee4ooDTy6uf1MceCqPOPBUDnHgqRziwJOLiysjceAprjh4EE8ceIonDjzFFc874okDT/HEgae44sBTPHHgKZ448MxGc+Aprjjw5OL6N8WBp/KIA0/lEAeeyiEOPLm4uDISB57iioMH8cSBp3jiwFNc8bwjnjjwFE8ceIorDjzFEwee4okDz2w0B57iigNPLq5/Uxx4Ko848FQOceCpHOLAk4uLKyNx4CmuOHgQTxx4iicOPMUVzzviiQNP8cSBp7jiwFM8ceApnjjwzEZz4CmuOPDk4vo3xYGn8ogDT+UQB57KIQ48ubi4MhIHnuKKgwfxxIGneOLAU1zxvCOeOPAUTxx4iisOPMUTB57iiQPPn3iWhjqmTp6AiZOnYYbGLMxS0Cez5sBTXHHgycX1b4oDT+URB57KIQ48lUMceHJxcWUkDjzFFQcP4okDT/HEgae44nlHPHHgKZ448BRXHHiKJw48xRMHnulaA+rTJmHctHnYfPQGLh3dhlXzp2G6uqK+mTMHnuKKA08urn9THHgqjzjwVA5x4Kkc4sCTi4srI3HgKa44eBBPHHiKJw48xRXPO+KJA0/xxIGnuOLAUzxx4CmeOPBM41nQmD4ZE8ZOxdyl23DioS68KC/EWFzD3mXjMWm6otdkzhx4iisOPLm4/k1x4Kk84sBTOcSBp3KIA08uLq6MxIGnuOLgQTxx4CmeOPAUVzzviCcOPMUTB57iigNP8cSBp3jiwDOVNWZMw+x1e3HmhjYsXYIQBUlCjjA6i51LJmAyB55/rTjw5OL6N8WBp/KIA0/lEAeeyiEOPLm4uDISB57iioMH8cSBp3jiwFNc8bwjnjjwFE8ceIorDjzFEwee4okDz1SePnk81t+yR/inrwj1fIaLbwzhFU9BanaBA8+/XBx4cnH9m+LAU3nEgadyiANP5RAHnlxcXBmJA09xxcGDeOLAUzxx4CmueN4RTxx4iicOPMUVB57iiQNP8cSBZyqrT5+KlbvP4dLlU9i6cjyGrb8MyxAgyeIiB55/uTjw5OL6N8WBp/KIA0/lEAeeyiEOPLm4uDISB57iioMH8cSBp3jiwFNc8bwjnjjwFE8ceIorDjzFEwee4okDz9SeNQvq0yZh0sRJmDppMiZsuwXbcCCRA8+/Xhx4cnH9m+LAU3nEgadyiANP5RAHnlxcXBmJA09xxcGDeOLAUzxx4CmueN4RTxx4iicOPMUVB57iiQNP8cSBZ0aePoUDz39IHHhycf2b4sBTecSBp3KIA0/lEAeeXFxcGYkDT3HFwYN44sBTPHHgKa543hFPHHiKJw48xRUHnuKJA0/xxIFnRubA858SB55cXP+mOPBUHnHgqRziwFM5xIEnFxdXRuLAU1xx8CCeOPAUTxx4iiued8QTB57iiQNPccWBp3jiwFM8ceCZkTnw/KfEgScX178pDjyVRxx4Koc48FQOceDJxcWVkTjwFFccPIgnDjzFEwee4ornHfHEgad44sBTXHHgKZ448BRPHHhmZA48/ylx4MnF9W+KA0/lEQeeyiEOPJVDHHhycXFlJA48xRUHD+KJA0/xxIGnuOJ5Rzxx4CmeOPAUVxx4iicOPMUTB54ZmQPPf0oceHJx/ZviwFN5xIGncogDT+UQB55cXFwZiQNPccXBg3jiwFM8ceAprnjeEU8ceIonDjzFFQee4okDT/HEgWdG5sDznxIHnlxc/6Y48FQeceCpHOLAUznEgScXF1dG4sBTXHHwIJ448BRPHHiKK553xBMHnuKJA09xxYGneOLAUzxx4JmROfD8p8SBJxfXvykOPJVHHHgqhzjwVA5x4MnFxZWROPAUVxw8iCcOPMUTB57iiucd8cSBp3jiwFNcceApnjjwFE8ceGbk6ZMxfsd9uCYC3xyuYc/S8ZjEgedfKw48ubj+TXHgqTziwFM5xIGncogDTy4urozEgae44uBBPHHgKZ448BRXPO+IJw48xRMHnuKKA0/xxIGneOLAMyOrz8C0pVtx9MItXD28EcvnTcMMdQX9MmkOPMUVB55cXP+mOPBUHnHgqRziwFM5xIEnFxdXRuLAU1xx8CCeOPAUTxx4iiued8QTB57iiQNPccWBp3jiwFM8ceCZoWdhlvo0TJ4wHhMmT8MMDfpbYb/MmQNPccWBJxfXvykOPJVHHHgqhzjwVA5x4MnFxZWROPAUVxw8iCcOPMUTB57iiucd8cSBp3jiwFNcceApnjjwFE9ZBp4hIaGICA9DUlwkEmP/jNm6YqIihHUres+M/N8Azz9rDjzFFQeeXFz/pjjwVB5x4Kkc4sBTOcSBJxcXV0biwFNccfAgnjjwFE8ceIornnfEEwee4okDT3HFgad44sBTPGUZeEZHhsPGxRfbrhtj503TNN5F3nPbFLtvZX751mvGeKjvhJiocIXvmZE58OT6mTjw5OL6N8WBp/KIA0/lEAeeyiEOPLm4uDISB57iioMH8cSBp3jiwFNc8bwjnjjwFE8ceIorDjzFEwee4inLwDMhNgJaZq5ov/Qehm95hOGbkz2C/h64QRMdlt1Hz9UPhb9ly/uvlyzvtSbt8ibzbmPrVSPhSk9F75mROfDk+pk48OTi+jfFgafyiANP5RAHnsohDjy5uLgyEgee4oqDB/HEgad44sBTXPG8I5448BRPHHiKKw48xRMHnuIpy8AzPiYCr83dMHDDIyw69gILjyZ7Mf09Y98z9F77CKO3PRX+li2ftvcZetHyMTuSly+h/0+l5e2X3sfBu+bAh1jp7W3Dkdnb28oDzzVr1mDSpEmYPn16GjMQ+jNPnTo1Q0+ZMiVDT548WaHHjx+P3bt3CwHPlf2KiGC3Sw6R/sXFxfWviE3c2YETLvHF94Ny6P379/j48aP0Ly4xxSeXXFxcGSkyMlL6L67sVnx8vPRfXNmt79+/C8duuMQRzzviiecdcZWQkCD9F1d2i+cd8cTyztu3b6V/cWWn2LbnJ3iJoz8GPBccSbYi4Clbnhp4suUy4Nl9jSam7X8l3O52w2UjPDRwQmwmb28rA56WlpY4ePCgABb37duH/fv348CBA8KyQ4cO4fDhwzhy5AiOHTuG48eP48SJEzh58iROnTqF06dP48yZMzh79izOnz8v+OLFi4IvX74s+OrVq7h27RquX7+OGzdu4ObNm7h16xZu376NO3fu4O7du7h//z4ePHiAhw8fQlNTE48ePcLjx4/x5MkTXLhwAfb29ggKChKCnjv7zM4o8vDwUNjGzc39d5pduW1mZoqhQ4di6BBu0S3dD0MGp1rOnW0ePHgI7Ydhwr4Q/q2gD/d/7x+/AdoP/PfAzc2d2sk5gvK1/N/c2eIhND4O+7Ht+ViZnRa2N6sXafvzbZ+9Tpl32PZP2c7931oS+6xG57Gf3ebbXjxL8oxk2yf/zZ1dlsU+YxKyuytwZ5/Z3Z7c3d0VtnH/t/4t4PnGwh291mpi9I6nGL092Qxmjtj6BH3XP8bgTU+Ev2XLh2+RLt+cvHwsWy7tP2TTYwxY/1C4ve2OG6Z4m8nb28qAp5WVFXbt2iXc1nbjxo3YtGkTNm/ejC1btgjeunWr4G3btmH79u3YsWMHdu7cKZi9jpnB0j179gi3n2XQVAZOFcFTGUBlPnr0aAqQKg9TZWZ/M+jGzvhnt7blzj6zy/h9fHwUtnFzc/+dZmdMvXihhXwF8mLt1hWCV29Zxp3NZtt9zZblwn4YP3U0Nu1aq7Af93/v7Xs3oVbdGmjYtL7wb0V9uP97b9mzDsPHDkFB1QLYsGO18PtQ1I+bm/v/0ywvzFo4A7ly58SS1fOxfvtKhf24/7zXkLfsWY8SJYuh94Ae2Lp3g8J+3P+Nt9H27titHcpVKCP8W1Ef7v/G63eswpwlGkLeWbhyLuWdVQr7cf833rJ3PUqWLoGe/brxvJPNZrmmc4+OUCtbmm/7bDbLM/OWzRLyzoLls3neyWZvZXlHrQQO7D8oMBNFx9S4/zsHBgYKj31S1Mb93/q3gKe2lSc6rHyEdkvvCc/ylHen5Q/QY+0TdF2lmXL5CsnyLitTLu9C/Xpt0MK4XS8wfd8z4Tmf+++aIyn214BnRre0VXT7Wnkrun1taiu6ha28Fd3KVmZ+S1txxW6hwG9py8X178nM1Bz1G9bFe8QITkIUdzabbfd3iBb2g7bZC9or7xX24/7vDXzHFPWJmL90tvBvRX24/3sDH/Ho1R00adEIX5Ao/D4U9ePm5v7/NMsLzv42qF6rGkISffAJcQr7cf95vyODtnjHru1x9toJ+vcXhf24/xsDX7H78Db0G9xb+LeiPtz/jT8jAR4hDkLeCYj1pF9BvMJ+3P+NQXugc/eOOHnxMM872WyWa/af2I2efbvzbZ/NZnnHO8JZyDt+Ua70N8872Wkh7/TsiLNnztG/ubJb/Ja24inLwDM2Jho6hmZYsec8dOyDoM1sJzH7+4G+M3affYALmkaSduny+7qO2EXLLz4xSbH8zAN9TFywCXO3ncfU/Vq/BTzZ1Z0MYM6cOVOpPGPGDOGqUUaaubJf7NaXwcHB0r+4uLj+FZkYm6JOvVoITvAWHBjnyZ3NZts9KN5L2A+ar+4g5nOwwn7c/70ZWBs7aRTU504T/q2oD/d/77ivobh2/wIaNqmPiPcBwu9DUT9ubu7/T0d8CICJvS6qVq8ClwAbhL31VdiP+887KJ5y9LcwtO3QGodO7UUCIhT24/5vnIRIbNy5Fj37dhP+ragP93/j8Pf+sHAxFPKOg48l5R0/hf24/xvHfw9H+05tse/YTiTyvJOtZrlm696N6NKjE9/22ezwd/6wdjcR8o6dpxn9zfNOdjoBlHe6tMWZ02elR8+4slPsgjd/f3/pX1zZqSwDT3ZLVl0dbZw+zs5OSqvEuGg8eXgPro520iUSxUdH4PGDO/BwdZQukcjB1hLz1Sdizpo9GLxNCx2XP+DAk+uPigNPLq5/Uxx4im8OPJXHHHgqhznw5ObmzsgceIpnDjzFNQee4pkDT3HNgad45sBTPHPgKa458BRXHHiKp98Dnrq6wjMrFSkiMgp3796FrW1K4BkWFo47d+7AwTEl8LS0ssL8mdMxYcludFz1DB1WPcXeu1YceHL9MXHgycX1b4oDT/HNgafymANP5TAHntzc3BmZA0/xzIGnuObAUzxz4CmuOfAUzxx4imcOPMU1B57iigNP8fRbwNPAwADbtm2DlZUVLCwsUtjQyAhPnjzBmzfaKZcbGgrLtbWTlzNIeevWLWioT8eZy7dw+akZRsxcg3M3HiE+Lkbh+6c2B55cPxMHnlxc/6Y48BTfHHgqjznwVA5z4MnNzZ2ROfAUzxx4imsOPMUzB57imgNP8cyBp3jmwFNcc+AprjjwFE+/BTz19fUFgBcYGAj/gADaiRKzB7I6OjlBU1MTRkZGwt+y5Q4ODnj48CGMTUx+LA8KCsLzFy8wafJkvHnzCh4ujpg6cSxuXL2MuLg4he+f2hx4cv1MHHhycf2b4sBTfHPgqTzmwFM5zIEnNzd3RubAUzxz4CmuOfAUzxx4imsOPMUzB57imQNPcc2Bp7jiwFM8/fYtbY8fPy5dVUpFRkUrvKVteHhEure0nTBhArRevoSjoxMmT56Ma9euceDJ9cfEgScX178pDjzFNweeymMOPJXDHHhyc3NnZA48xTMHnuKaA0/xzIGnuObAUzxz4CmeOfAU1xx4iisOPMXTbwFPHR2ddIFnbFy8cIUng5fyioqKFq7wdHF1lS6RyNrWFlOnTsW5c+dw//59TJ8+nQNPrj8qDjy5uP5NceApvjnwVB5z4Kkc5sCTm5s7I3PgKZ458BTXHHiKZw48xTUHnuKZA0/xzIGnuObAU1xx4Cmefgt4GhsbY/Xq1bh06ZLgi1Kzf586dQrbt2/HoUOHfrSx/588KV1++HCK5QcOHICGhgZu3b4NbW0dAX5y4Mn1J8WBJxfXvykOPMU3B57KYw48lcMceHJzc2dkDjzFMwee4poDT/HMgae45sBTPHPgKZ458BTXHHiKKw48xdNvAU9TU1PhSkwGJ9XV1QWox/7NPH26BDgyyMfgI4OZ7N+sv2z5dLnl7PVTJk/G02fP4OTkzG9py/XHxYEnF9e/KQ48xTcHnspjDjyVwxx4cnNzZ2QOPMUzB57imgNP8cyBp7jmwFM8c+ApnjnwFNcceIorDjzFU5aBJ4NHPj4+MDAwgLm5OW7cuIH9+w/A29sbXnJmf1tYWOLChQvQ0tL60c7+b2pmhvPnz+PV69fC327uHkhISIC1jQ0mTZrEgSfXHxUHnlxc/6Y48BTfHHgqjznwVA5z4MnNzZ2ROfAUzxx4imsOPMUzB57imgNP8cyBp3jmwFNcc+AprjjwFE9ZBp7MDCCxnffhwweYmZlh7dq1AvhM7fPnL2DXrl04duxYiuXseZ07d+4UngMqLLt5E1euXMGevXuFKz858OT6k+LAk4vr3xQHnuKbA0/lMQeeymEOPLm5uTMyB57imQNPcc2Bp3jmwFNcc+ApnjnwFM8ceIprDjzFFQee4um3gKfMbAey53nOmDFduGVtarPb1c6ePVuAmJlZLoOD7NmeHHhy/Slx4MnF9W+KA0/xzYGn8pgDT+UwB57c3NwZmQNP8cyBp7jmwFM8c+AprjnwFM8ceIpnDjzFNQee4ooDT/H0R4Cn7Pa2RkZGMDEx+SM2NDSEk5MTIiIiFL5nanPgyfUzceDJxfVvigNP8c2Bp/KYA0/lMAee3NzcGZkDT/HMgae45sBTPHPgKa458BTPHHiKZw48xTUHnuKKA0/x9EeAJ4ONstvb/klHRkYK61b0nqnNgSfXz8SBJxfXvykOPMU3B57KYw48lcMceHJzc2dkDjzFMwee4poDT/HMgae45sBTPHPgKZ458BTXHHiKK8a2OPAUR38EeCqDOfDk+pk48OTi+jfFgaf45sBTecyBp3KYA09ubu6MzIGneObAU1xz4CmeOfAU1xx4imcOPMUzB57imgNPccWBp3jiwDMbzYGnuOLAk4vr3xQHnuKbA0/lMQeeymEOPLm5uTMyB57imQNPcc2Bp3jmwFNcc+ApnjnwFM8ceIprDjzFFQee4okDz2w0B57iigNPLq5/Uxx4im8OPJXHHHgqhznw5ObmzsgceIpnDjzFNQee4pkDT3HNgad45sBTPHPgKa458BRXHHiKJw48s9EceIorDjy5uP5NceApvjnwVB5z4Kkc5sCTm5s7I3PgKZ458BTXHHiKZw48xTUHnuKZA0/xzIGnuObAU1xx4CmeOPDMRnPgKa448OTi+jf1+8DTS4ARyVbQJ0U7OXV7asv1zahN4lTtqf3T/qnaU7SR5dsUtKdoU9CeGf8p4Jn6syS3pVyewnKvV+SM+qVYDzl1e2r/rH/K9pRtP42zFG0K2jPpPwI8U3+Wn7Vn4rNm1Dflusip2lM7df/sbs+MOfBUPme8X1O2pW1X7B/9M2qTOnV7av+sf8btKdt+Of9wZ7t/F3im3J+/Gi+KLNc/ozbBqdtTOUVfRf1/0p6iLQvtPzHr/zvAM+V7kzPsk7ZNkTO3LolTt6f2z/r/1+0/8+8Bz5TvrXD7yrWnaUtj+XUxK+iTUVsqp1wXOXWfn7SnaMtEu3xbZvy7wPNn7/+z9tRO2V9Rn8yv6+d54SftKdqy0J4J/xbwTP3+qdpTtCloT+3U/TPso6AtteXXxfxn21O2pW3/uX8PeKZ+f0V9Un0HBe3JlusnWEGfjNpSOeW6yKn7/KQ9RVsm2uXbMuPfBZ4ZvX/qNolTvj61U/dP2yejtlSWW4/Eqfv8pD1FWxbaM2EOPMUVB57iiQPPbDQHnuKKA08urn9TvwU8qXAMTvJFxIdARH0MIgci4p0vguWKyaB4b4S89ac+rJ05AGFJ3ulPZKT9I6lv5Hs/hMR7pGrzozbZ+wUg/K1P+sUr9Q9V1P9HHy+EJPnJfX5qZ59Ntj72eppkyL8+xWen7ZWi/cNPvls6/n3gSQV8gg/C3wdIPyf7LP4ITZBMNIIS5beBvAMRlqhofWS2bxN9ES7sN/peCfLtsjbZ+wVK9lWKPvKWxYlc/xRxQu0JtL73ss+YKo7oswj76cd3UNBO+zlFO+1n+TjMrH8beCqIGSGmUrQHUDtry8xnlezbMHoN659iXWSh7b2/sB5hfWy/J6Y/wZT0TxUncv3Z71X2XoJp3cnt9FkSKc7S7Hf5dkVxkf7nSc8ceCqXM44bFqPyv9/U7QqcIr+kzkNZyC/UP0V+SdU/ZX6U5h9ZO/ssGY1jP8s/3KI468BTPvYyHy/pxx9ZiCEWI1S3UOynrFt+MX5Y/wzHM1m8y9oldU1yvP6kTqL2NHXRL9YtbF1ZBp5CLqFtKrw3mbZXGOWK5PeXjnnSfBKeJN+mwLS9JPuL9We5RD7vUBsbs+RzF+1rWW2U1qx/xrknZS6UtSfnQkW1TvLr0+aalLVQ5px14Jk6dgJTxg6zED/SGlz4bHKxnMbS2E6vhiYHCXWypOZhcRwUl8H6flZTC7Er306xI9cu2Tfp10PycaWoPTP+HeD509j5yTiW2inHXQV55UfuYfOpVHkptX8576SKHdo3P8s7srj60f6LeYc5y8CT3v/nsSP77JL2jGKD1cosVlP3T45VWe5h60ydl1I7vbyTOnazGjss77DfqfSzsvYs5p2sAc+0saNw3iMfz2x70vcLkG//YQV5Rz7WyJL9k5x3gv/2vEOfL6vAM8PYiae2H3EhcwAi6PulXo/MbH3yeUeIJfk8JZ936Lv+NO8IfZPX97O8k6Kd9s0v551UsZIZc+AprjjwFE8ceGajOfAUVxx4cnH9m8oy8Iz3RVSSG+y1T2H6kH5o2aY5WnbshnF7zsM6MgihVOAGvQ1AUIQdXl1ehCmDqJ36tOs3BDsfPYPXB7+0E92kAMS9dYXhvdUY2qEFes5eiwfe4Yh864mABD/EJtpD58ZODO/RRVhXq+6DsPjSI7jHBdPEKOW6AhL8ERtvjefnN2Ngl46S/r2HY93dV/BKYP29EfXVA4Yvd2HMoHaSz993NLY+1oNvIrUn+SMm2hS3D6xAr46S9laDJmCPlhH8EgOp3Q8xkUa4snMJundoI2kfOhVHtM3gnxhABX7Kz5ORfwt4sskCTapDvJ5gx7wpaMO+R5sW6KCxBpqunohIcIfb81Xo0rmF5DtK3aptC7Tt0QNbXzvBn/ZlioknTYDYZMrX9hKWjG2B9n36Y48B7U+aOASxtiRPeFhew6JxwyTra9ceA9cehGGgZIKaYr/SuiOT3OFkcB4zhw2Q9O/QGSO3n4JFGG1HWmf4J1+4e93F6ll9pO1dMX7vBdhGBdOk0g/RSS6wfHYUE/v3krR36omph6/BIZrtJ9oPiU4wfnAAY/r0kLR36YNZp+7AOSZtXPzMvwU8EynmYs1w9/Bq9O7UXvgsrQaMw85nBvBNoN9Eki+io8xwfe9o9OhIn5N91rZ9MePkHdhGe9N2SjsBDqbfUEyYPs5sHISOtM/UzzyHfVSQAIjYwa7I4Dc4vmYOtbWk9bVAq/HzcNnCnj6LX6p9Kpk0hvk+x55F09COvTf1bzNtOe7YuwjrCkmiOEo0w4X909ChnaS9w8y1QhyFsNeyCbDLA2xQH4dWwutboev8zXjhQZ+TtdME3s/hNlZNGSX5bm3aoufSnXjjQ+tlMS73vX5mDjyVxdK48dPC/iUzKG5YHqG4mbIMt+2cKW7oN09xE+p9Fjvnt/+Rf9
Но спортивного интереса ради и общей пользы для:
=СМЕЩ(СМЕЩ(S2;0;СЧЁТЗ(T2:Z2));-(ЯЧЕЙКА("строка";T2)-1);0)
Первый аргумент функции СМЕЩ "ссылка" задаётся смещением на последнюю заполненную ячейку в диапазоне дат.
Позиция последней даты определяется подсчётом количества непустых ячеек в диапазоне дат.
Второй аргумент "смещение по строкам" нам даёт функция ЯЧЕЙКА, определяющая номер строки. Поскольку смещение необходимо производить вверх, до заголовка столбца, номер строки нужно перевести в отрицательное число.