Запрет ввода повторяющихся значений
Простая задача: есть диапазон ячеек (допустим А1:А10), куда пользователь вводит данные с клавиатуры. Необходимо обеспечить уникальность всех введенных значений, т.е. запретить пользователю вводить значение, если оно уже присутствует в диапазоне, т.е. было введено ранее.
Выделяем диапазон ячеек и жмем кнопку Проверка данных (Data Validation) на вкладке Данные (Data). В старых версиях - Excel 2003 и ранее - открываем меню Данные - Проверка (Data - Validation). На вкладке Параметры (Settings) из выпадающего списка Тип данных (Allow) выбираем вариант Другой (Custom) и вводим следующую формулу в строку Формула (Formula):
=СЧЁТЕСЛИ($A$1:$A$10;A1)<=1
или в английской версии =COUNTIF($A$1:$A$10;A1)<=1
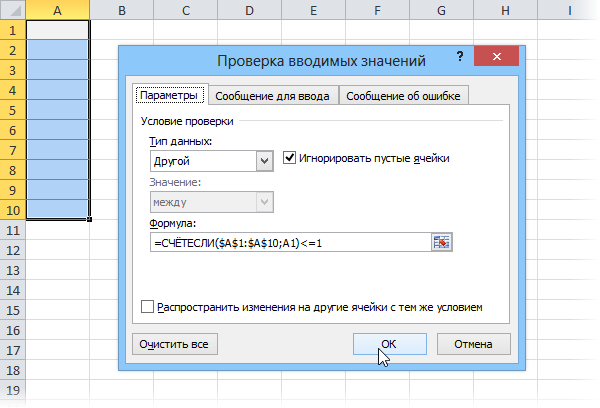
Смысл этой формулы прост - она подсчитывает количество ячеек в диапазоне A1:A10 равных содержимому ячейки А1. Ввод будет разрешен только в те ячейки, где полученное число меньше или равно 1. Причем диапазон задан жестко (абсолютными ссылками со знаками $), а ссылка на текущую ячейку А1 - относительно. Таким образом подобная проверка будет производиться для каждой выделенной ячейки. Для полноты картины можно в этом окне перейти еще на вкладку Сообщение об ошибке (Error Alert) и ввести текст, который будет появляться при попытке ввести дубликаты:
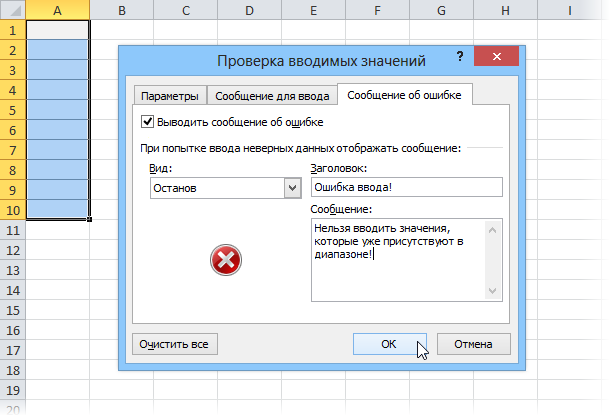
Вот и все - жмем ОК и наслаждаемся реакцией окружающих :)
Плюс этого способа - в простоте реализации, а минус - в том, что подобную защиту легко отключить в том же диалоговом окне или скопировав и вставив в наш диапазон ячейки с дубликатами. Против лома нет приема. Для предотвращения таких террористических действий пользователя придется включать уже серьезную защиту листа с паролем и писать специальный макрос перехвата копирования.
Но от случайного ввода дубликатов подобный способ вполне предохранит.

У меня уже стоит проверка по кол-ву знаков при вводе и надо в том же столбце исключить повторы.
=И(СЧЁТЕСЛИ($A$1:$A$10;A1)<=1;ДЛСТР(A1)<20)
Например задача. Необходимо создать список сотрудников и ввести их табельные номера. Понятно что табельные номера должны быть уникальны.
Мы создаем программку не дающую возможность вбить дублированный ТабНум и сажаем девочку за эту работу, Через некоторое время выясняется, что работа встала, потому, что девочка подошла к очередной фамилии, завела ее, а табельный номер, ей программы вбить не дает. она тупо смотрит в список и говорит, ну вот же, здесь написано, Иванов, номер 7534, а Ваша программа не дает его занести. И оказывается, что этот номер действительно правильный для Иванова, но ошибка была совершена ранее 50-ю десятью строчками, при вводе Сидорова, и вместо его номера 7543 он ввела 7534. Приходится искать а где же это раньше она совершила ошибку? В результате работа по вводу (срочная между прочим) останавливается и начинаются судорожные поиски. Поэтому общий принцип такой: Если вы посадили человека (часто малоопытного) за вбивание данных - разрешите ему вбивать все. Ошибки найдете позднее и его данные "причешете". Вывод: Если Вы профессионально занимаетесь созданием больших списков - время дороже контроля ошибок.
Помогите разобраться.
Есть таблица с колонками Дата; Время; Показание. Ввод времени и показаний осуществляется через форму. Временной диапазон занесения (0:00, 0:30, 1:00 и т.д. до 23:30). Это повторяется каждые сутки. Меняется только Дата и показания, временной диапазон остается неизменным.
Так вот, как сделать проверку на случайное повторение временного диапазона привязываясь к дате на текущий день, занесения данных?
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAA14AAAJGCAYAAABLKlSwAAAgAElEQVR4nOzdv27bWP7//5d+2JsYd8ZIwSCT0hXVGbvAykECV2lGQKpQmClW+hZ2FSAwkCouPtQWu7BSBdA0qYwEkQbYgTupcukJBqYG6pzLOL+ClERSpET9oUTZzwdgIBHJw8NzeI74Jg+PCsYYIyzsjz/+0I8//rjtbAD3Hm1tdZRhvlE/20cdrIbyQxLOjbD/b9sZAAAAAID7jsALAAAAADJG4AUAAAAAGSPwAgAAAICMEXgBAAAAQMYIvAAAAAAgYwReAAAAAJCxws3NDb/jBQAAAAAZKvADysvhB+GAzaCtAQCwm/gOD2OoIQAAAABkjMALAAAAADJG4AUAAAAAGSPwAgAAAICMEXgBAADgARqoWa6pu+1s4MEg8AKwQwZqlgsqFOb/lZuDTHPSrQX2V24q272lNdCgW1M5WEblsmrNrgaSBs3m9AXGoKtmraxyqPzKKtea6kYOKnTM0b/Afnb7OLuqxR5fU4OkZbXtXrYNuk3VypNjqkUrDms0ULcZOI/Ktal24q0WqJNyTdPdUcp0xuvWVF6on9lkPhc5lm0alWOw/Zb08cWJKhvMQ7Mc/s7o1soqFAj+HgyDpdzc3Gw7C8CDENvWOraxJCPJyO5EFrqmY8tYjptxzlzjWH4eLMdkvbf52ekYO5CfjhtcNCov23RM3OeWsQMbuB1nXL5T5eg6xo4sc4P1kXVZbOg4Xcf29uGfY4GtJvUuy2R+ms3TCeQz8DfVLLAWHXu6rKPnm3H988qvhI5tTZ0rqdIxruk4y7WtTeYz3bFsX1w+rS00FLdjG8sK5sMy9tY7kuxwvRxG4LUkTiRgM2LbmuvMCLy85dl/keUp8OqMg6HY8jDGL7PAxVDggj02SA0sDyfZmQq8vNU3cdG/weNM3C4YeG374rJjbHsSfLqONftYsRrXMdY4CHdD53xcWxifT6NzafRBynRcxwpfoKftZzaZz5T72rqO7QWVnRzl6YHgejmMoYYA7p9iXRf14rZzsTHd2pFakiRLzknCoJliXa/t0X8Gar5t+f+29TqurConcizvn62384c4lR5b43/f3GYzzigPx5kvFV1c1FXxD6tYf63RoT959HDO/815qg8XFXklW1TlxJE1tU5Xl62pDz2tS384WZp0pGK9p17PqGPHLMxNPtMdy7Z1L2/kuD3VK7QLbBeBF4B7a9Ash97RadbKk/dgpl5m8Mf/B98Tq0XfWRr44/ELKpRf6uP48496WY7ZpluLvCdUC7yL4/3VunHr+QFAt+nnpxzz7sV4J5MLKOuFns64rqhcXHjvMgy+6GN/tM1jlWLXLurRE/+f/Y/6Micicb/2x/9OvOhPWx7xG+fiOBey0PGmOf9mGHTVLHuBqeW4upjx0kqoXRQKKtSaU+9OButh0K3Fvr8z852/0XuWg2bkvbrg8U0Hukn7StuWU+Upqb3NUywqdNoVH8k7dSy9GJ2Qg1vdJCZwo9tBynRWscl8LnUs0+9Keu/kBt7hLTfVXdN5KnV1qRd6qm64/UXfRVu2v556P2v6XeT4fn6B/m9qn9GyG+26OXWMzcgLd1PtP1X/i7XZ9iO3XcWjU2AzlhpqGDA9BG4yXC24qbee5X0W8x6Tt1srMOQnOtRw8v/4IXijYWnxw+Xi1nPszmSfM4fWLTgUqRN+fyl92YXzH/uOV+r6mF0eWz/ONQ01XKz+Z59/qY5TMrLsOe+exQyTdePfdxudf95no+28Y+nYtj/MMZBeYJjaeLjvOH+j94dc49jTZTBrX+GyTG7LafM0XS9LGB1X8HyMG7qaOGx3RjqhxSsOad5QPlOvY4z3rmZse+4Ye/z/9Zyn3pBcv4+aStuK+R6Y314nw3qT3vNM38+n6v9C+wycs8F2Nioby/GXT8ovnLRrHHtUDvFDx9eJ6+UwnngBeBgsR97otIqO/aE7waFl3lC5vm5uu1LxUUwCXZ03vMcn1ounmr6XW9TTF94gm37jfHwHNDgEz0vmUuMHN48nz2Ci6w2al9JJRUX/cYx9vLl5t9LqN0oqFAoqHbUky5LdceXOetSi9OWxdaXH4yFT/Y9f/PNkoG7zpRr95M2mk0keeDVd/7POvxkqFzJuR47t76vfUuPlrKc4gad8449GTyqCRuf86OnFaLuWLrv+k8Wkhxoph/tOymD2vsIbJbfldeQpre5lS5Il50M9pj/YfDpZp58mndT7KlZ04frDEvsNnY/quHurx6/r46GL6zhPNbjVTaulvoJ996i/7sd8D8RbR/+09v5vfE4P1HzZGB+j1wtPvpPCw6iLevR48V1hPQi8ADxc/a9y/X8W6z0ZY/Th0a1qtbfTw3BmDs2J8ofqTKXRVPntzZx3IFo6KhRU+vhYjyTvotqYmUPHFhYIKnRzm2KYlaW4awLLcWW8SZrU6/V0USkudmGXqjxWsMpxFuv60LHHF4alQlnl2hfp6evxO2GL8eq1UDhS3Ks1c8+/eYoV1S96ckeZW3DY5KD5djpf44vCvholbyjSkb/Scu/xjdIpqdGSLLujD6NAaNV9BdryYkb1UvB+kiDtPOiDpt62JLvTUyiWC55zU2LaUVI667LJfC56LMWnehF5v7J7KT2dOUx2tfM0dhh07Lkzu70GNh7vc+Gf1Fhr/+fqa8wNodGNu3B/MNDt17XsFEsg8AIASaNx+aWjrzq+eB1zV3ViuYkLWjp6+VEvPsxOW7LV6dhSv6GjUoox94GLl9QX26Ftki5YB7odXf3PeadqOWnLw7eF4yxWLtTzA0tjeupd1FUpLnvX21bHGBnTUfxcCenPv1kmE2w80azTdDwJQr+hl+Wa3KevE/Ll575jxkG2MUa9paIES45rZIyrjmOp3zpSKeb3i9azr7S8enEdW+r31ToqpXjPpataqSHFvUsX+0RmJFonM9JJIe5dndD7PhvN5zLHUlR9NBNOv6HzZlOXj8OjCdZyns481sSU5rTXEf+cdjuy+321GkcqpXpRasH+b0mD27hbOK6+6lEmT1cxH4EXgIdrPOHCQM1yyRtCZh/H/5hm4Mt7/h34+Ite+3XKO8GVi/FMZq2jWRNrSFJR9Q+jmcT6apwnfekP1BxPZhDcJmYolyR1z8dD6uzX2QyBSl0eknb5OOdLcf7FbdUsx0y8UtJjK0U6xfo4qOz1EobnBZ6KrHemyqIqT1+E62XVfSVOnpIyR/Xj8QX27P0P1Cwf6cZxQwHh5Ee7J8Mfp4TqZF46afLcCwUZ4SB1k/lc4ViCs4o2vuo42iGs5Tz120TS8hXPHS+fgfIczwo522L93zyTY4wVvKnUvZRyOHT9oSDwArB73MA4iVRDyCT1P+q8O1BwdrzJhXZ4mMYgdljh5It18s5P0EBf/Cn0LOdkfOEyme1vevhO/+vkGYwbGSdSuRjdae3PeV9H3sXJaFhc62hqNrxBt6la+aV0EggsAtu0jsJDrAbdpspH3rsadidyB3twG5v/tNKWR6xNHmfyEYTOlXkxQrRegybHm+b8S0q7r0ZpclyD7rk+ylZnHWNTA1Pz9xsvx7OjDbrNOTcD5hmoe+69jzI+DxbZ18y2vGSOAu/azHqiPfDf8Ru93zj6K33U+OJ99JSm5Uf63lOH8E8gpEnHX1OTFpd+OOUm85n+WOJMnnoF+82FzD13Jjdgxn33oKtzv78Onjvp2muMQXDW1eRAbqX+byxuKPukHIPvpH6ZOsaBmpePNa7ihYbQYy02OpXHPcIsLcBmhNtacEa58F/SjEzBGcE6gZmooj+wPF5m2cbpBGZds2wz+c1N1zj2ZL3xj5talrFHMxqOf0zUxM42Z0fyb3fi1puewSvVjGauazqOHf7RVVnGCvzIbuw2tjXZz4xtgrPKTR1DGmnLY8vHmbjbwA8Uh/6SMr3A8aY7/6IZ6kTSs8LnX2rT7WpySF65BY8h2tSi50WoLQbP4Wib9Y81mI9Z+0rblufmKVov4/1Zxp51MiRtF9f/uM6kbqJlljKdpPY2b/a7jeZzkX0lco1jJc0OGF1v+fM0dKyBtpZ4vGn766n2l5DPVfq/pO+IqSKadYyBGRQT/lL35QvgejmsYIwxwsL++OMP/fjjj9vOBnDvrdrWujX/RWvLkdtb51CywPCwtacNICq7toztGqhZ+6KnF9RptrqqFd7qcefD9A9JD7qqvTySXq95IidxvRzFUEMAAABsjv9jx7WupMEXfT0m6NoI+/V00CV50/u/nj2NCNbjb9vOAABshD+rHV/uwI6jLe+8we2N947f7cCb6+Fi2zl6CCq6mFXOlQtRDdnjiReAe2vQLI9/z8X7XZZ5MwSm162VJj+k22+knEIYwDKybMvYvOLTF7ItbzKMy+P6cpNqADuocHNzwzteAAAAAJAhJtdYEi8LAptBW1sdZZhv1M/2UQerofyQhHMjjKGGAAAAAJAxAi8AAAAAyBiBFwAAAABkjMALAAAAADJG4AUAAAAAGSPwAgAAAICMEXgBwIPVVa1QUGHqryZ+DhoAgPUi8AKAB2rQfKtWzOeWc6LKxnMDAMD99rdtZwAAsA0DffkoOa5RvbjtvAAAcP/xxAsAHqLuuRr9vhqlggrlssq1rgaDbWcKAID7i8ALAB6g7mVgkGG/r37rSKVSQeXmvOgr5r2w2uSNsG6t7H1WrimUVLcW8y7Z5K8WfKls0FWtXJ4sL5fVjH3pbKBmLbpeNP8z1hk0VY7kI+74B83y7PwCAJACgRcAPDSDpt7Gvdwlqd8ozQm+KrpwHVmj/9odmYuKn2xNl8cf1LEl9VtqnAeik8qFXMeW4xoZY2Q69niRZXd0MXqprFtToXSkmxcfZIzx0+qrcVQOB3LqqlYuqdHqy+746fX7ahy9DKw3Z51iXb2OHTgWRx9ixl0W6z0FsivLcSf5BQAgJQIvAHhoinX1jB8Aua46TiD4kNRvnC8xq2FX518f66RSVOmxl5p9nDI6eVyapOI/iet//KKBNE5L6uurO9lk0HyrVl+SbB1XJFWOZVuS9ESPFlhHpceBjDxS0utuk3xITx7xUhwAYHEEXgDwkBWLqtQv1DNu4KnOjW4Xet9roG7zrXRcV1HeEyJjzFJPhUqPw0Fg0v6+fOx7/7QeywvbKrroGRlzoUox7ToAAGwOgRcAQFJRlQtXzvyoJ6x1pEKhpKPGEz3W6rNzFOsX6hkj98MjnZfLevkxbi1XX/vzUkqzTkTrKPQuWK3ZXcMRAQDgIfACAPiKevrCkvREqUfT2R3/SVlLjaOSCuXmisGKNxlGqXQkve7pw4u4dUqajED8KjdulVTrRNgdGWPkuo7sfl+txpFK/Jg0AGBNCLwA4MHxZyYs1zQ1CaAW/wHl0JOyfkOlqVkOk2YljBqo6U+GIcvRSWIminr0ZPTvli5j006zTkLqxbqOlx52CQBAPAIvAHhoBre6kaR+S0elsmqB6dXPv76Indkv2a0GKqre6/gTV0hqHXm/C6aBbm/6kvr6eNvVl68aP0kb3MalFRge2P8qdzCQ9CRuRVUuOhrFRq2jUQA5ULc2mcY+zTpyv04nPuhqMtu+9/TPDY5bJBIDACzDYCk3NzfbzgLwINDWVhdXhm7HNpZkNPqzLGN33BSpdYwd3E4ysjvxyywnsB/LTFazw9tL42WuY/nb2sbLjmscy1vHsh0TyqHbMbY1ScMab5NyHdcJl0HozzKW7ZiOG8hTTH7XgXN8+6iD1VB+SMK5EVYwxphNBXn3yR9//KEff/xx29kA7j3a2uoow3yjfraPOlgN5YcknBthDDUEAAAAgIwReAEAAABAxgi8AAAAACBjBF4AAAAAkLHCzc0Nk2sAAAAAQIaY1XBJzNICbAZtbXWUYb5RP9tHHayG8kMSzo0whhoCAAAAQMYIvAAAAAAgYwReAAAAAJAxAi8AAAAAyBiBFwAAAABkjMALAAAAADJG4AUAAAAAGSPwAgAAAICMEXgBAAAAQMYIvAAAAAAgYwReAAAAAJAxAi8AAAAAyBiBFwAAAABkjMALAAAAADJG4AUAAAAAGSPwAgAAAICMEXgBAAAAQMYIvAAAAAAgYwReAAAAAJAxAi8AAAAAyBiBFwAAAABkrCDJbDsTAAAAAO6fm5ubbWchNwrf7u4IvJbw3d6evt3dbTsbwL1HW1sdZQgA2Ibv9vZkDKHGCEMNAQAAACBjBF4AAAAAkDECLwAAAADIGIEXAAAAAGSMwAsAAAAAMkbgBQAAAAAZI/ACAAAAgIwReAEAAABAxgi8AAAAACBjBF4AAAAAkDECLwAAAADIGIEXAAAAAGSMwAsAAAAAMkbgBQAAAAAZI/ACAAAAgIwReAEAAABAxgi8AAAAACBjBF4AAAAAkDECLwAAAADIGIEXAAAAAGSMwAsAAAAAMkbgBQAAAAAZ+9u2MwAAAADgfvrjjz+2nYXcIPACAAAAkIkff/xx21nIDYYaAgAAAEDGCLwAAAAAIGMEXgAAAACQMd7xAgAAMw3fP5f15nr2StW2vr073EyGAGAH8cQLAADMtP/qk771zlQ96+nb3Z331676S6s6690RdAHAHAReAABgvv3vVUpYVNzfaE4AYCcReAEAgDUaqnX6XN/t7Xl/z0915S+5Ot2bfB79O72au/2Uq9Pk9Pb29N3ec7WG3lDJ0WfPTk918jw57eH7Uz0LbH/yfjh/f89PdTWMpHMVSCeyPJif6N/JVYo0ovk4vYqUrXfc89eb7C983Ml5ArA8Ai8AADDf8C/p+3mPtoZqPS/rzZ8/6Ne7O/1alXTd1k/joKqqX+/u9K13pgNJ0oE3TPGurWqq7SMO36l/5qWkgzP174JpSQdnTdn70v6rpkarXf9Z0i+f7rztrtv66fl7jeIZ7122tuQPqeyfSe03ZT0bBV+H77w8BfY3TqceSac6Sqensx/a+qk8CfL2X33Sr2ej/PY0OYSezg9TpBE97neHOnw3fdzz1/P3N3yvf71p61pStd0L5UnV9jhPAFZD4AUAANbr+k8NgrHSn39pKOnw3TvFX8Mf6jz4jljC9utw8Ozv2pe0//dnXvB3/Vn/G0rSlf7z5lrSgZ793QswR+tcv/lv8lO3SLrT6ezrH6UDSW11Uz85WkcaSUn/pnb0s6Erb+qUqiqH4eD6oMQ4UmBdCLwAAMBcw98lzb0G35f96U7f7poq/vZc/zd1hZ/19ovs6nv9IEm6ljuUNPxLfyau/KcG0cjv+o2svT1vtsfqmf7tB2uTdK71puwN1RvNCPnnX+NnYhq4M/KWKo1wPr7bq04HVFOudPKbxk+8xg7/6X/W1v+9X1eICyCKwAsAAMw1lPSPNA8/hu/1bK+sn9TQ/5u6wt/A9psyGmrYrkrtN7LK/ntVkxX8YZSTv8+vRgU4lKvv58exM9MI5yM4xDLJ/05/U+XdP2OWHOrcH/55/aas7/bKmvfrAQAWR+AFAABmG75XV39PEShc6aT8xntX6J/LvBi06vYLGD9VOlBpX4EnYHF+SJy5cX/8tMh/chZ4kvb594SnR8O/pFnHlyaNRV1/ln5OGuoZ3OeBznqBd7wArA2BFwAASDS8eq+T/0q/RJ+0jAWG4YWG6w01SB67l7CzFbdP4frz77oaSsPf/feaDp75T/IO9cvZgYLBzvD3z7qWdHD2c2LAMnwffWfqUBX/0dP1m/r4Kdjw6r3/76Fa/5V+GSc4lDv1dGleGstIDh4l6eq94x1HteFNzOG7dhl6CKxL4dvdndl2JnbRd3t7+nZ3t+1sAPcebW11lCGWc6WTVO8N+aptfXu3781KeC0dVNv69z9/07+qbV3rQNX2J392vGi6Vf16N3oSM0yxfTCLp/quGshhta1fVdVP448OdNb7JHs/kO7ZmX74/Ebta0kHVf36KfwUaPj+dDzDn3Sg6llT56OgM7q/8W4OVG00dX44GUp4dVrXT20/ojqo6qz5Tvb+/DKttu/840xKY4HjHs5bz9tf5bc9/zOvLvbfPx+/UxbOE7CY7/b2ZAyhxgiB15K4kEnv6vRUSpzJCpiNtrY6yhDL8YOEg6rOGj/LPox/XDK8OvWCo2pb397ltacPBl696fekNuZKJ3uO1A4Gab7hlVr1qtwGQQ7uDwKvsK0MNZz64cDAb2h4rsY/bvgs6bc7EGOo1vOYHz8cl+GVTmaW+zqycKWT5+H6/Un/3FDQ5R/f6ZV/XH55ZHGc2DEJbWNv8rs6k34p+oI88JB5T4SSgi5J2j98p8/tPM+CkTPVxnTQJUn7h7IblCNwn20l8Np/9Unfeu3Ji5vXb/SvwPSlw/d/qfLJe7Hzuu1wEZSaNw1vvz36YUqNfzDRc6jz0Y89Vtvqf3qV4kXpRVzppFxV+zowWD20/6wd6pd2VQd/Vv2pdct6c32gaiPNC+G43/wpqgMXhwfVtr6Nhjddneo/avo/NHqtN//lhg8gSaqmvHF2+LPOSlln5j6I/F7Z1OJ3PO0C7rHtTa6xf6h/PJtMmRN6eVTSvvb95bNfBsW0/cNX+vcoqr1+o/+EriGv9J/Pz9R/d7j2YGT43tGf1bY/ra3/t/bgbrb9w3f6/Ck49e6n+DuLeJj2S5ObEoEfBb36Taq82tf+996cXtV/cs4Ac4OEkH3Zr/IbMQzf18fTo1+/KesZv1UFYAu2PKvhDzo7G92Bnr7LvP/q0+SONBay/6o5fqLYrgaHUzlSIxAMXZ2Ghl49ez/U1WlwKFZ42NXw6lTPxkMVT3U1XjbU/9xn+vc//9K/nk+2PbkKbBzZ13enV/H7islTUHSo6slVmrT99aKi2039eXkK7vPZ6el4KOx3zydlO7+MYobZRvM3fD/Zdi+SdmhZunqJlkH8ENSH7krd0XDYw3f6dncXCtZnleHknBqqdRqo23nnxd6enp2Gh8DOWw5ged71xIzfwgKADdj+dPJ/f6dfR7FXuxq5OB7q6nTy3sUJd6gWsB8YK+7/Ev3wvf71+VlgCltJh4HyPzjTv1/t6/Dd5EcYD86a42llh++fy6q2pbOevt31dPZDWz+V/QvM4e9y//wsq/pGetbTt7s79c+kdjVwZ/HwnT+US+MhiLH7islT6MgCQaWqbW9Yxty0e/HDN6LbRX6EcpSn4D6v/yzpl0/+kM3rtn4KvEM2s4zkffn/ejbaz+R3Usb52w88rVRb3UB7GE1rvFC9qKpf7+70rTcafjr6Mc75P7T5UAzfOzN/T+fwXU9nZ23/gq03fe6NXtr/8wf9enfnnbvXbf0UCGzDddRW9UC6br/Rf/wIed5yAACw+7YfeEk6/HnyTlK7eqqu/+/he28a1Wr7Tr9Wr9UODEdECoc/T4KFN//VyX8/64fGjKF/P3w/Y1jglf7z5lrSgZ79fV/Svv5ROlAwOPjzOrhc2v/7Mx34+1702cp+adYvN+6rmPwrl4EsR39bZT0OnnnvjI2OT9ef9b+hlKaM0vlB1ap3/G1nFNRd6X96Ng6Wfvh+VFOz93mYOJvkIkOI7qfrN2V9t7cn642kJZ4tHZQireX6Tw2C9fznX+O6C9fRoc794bDek7V5ywEAwH2Qi8Arepe//dn71zDwi4Lehbj/q/BIaV92cxTUttX+M/K0K8q/UByOfkQxaPyjltd6U97zL1iv/c2G0tDV1O8/ThKe/LjmyPUbfwKMOb8RM15vT88iw/Zmu9LJb8r2qc7+9/LiP/+8nFdGkqShBu78pEs/N7y8j4K6q7+kv38/vWKqfSLOwVlvPJlGu1qOH4qaij9xx11Txd+e6/+iJ3ToB2FjzFsOAADuhXwEXooMHxt9Fnjq4QVhB4reZMYc+6/0//zoo5rwtOvw5zNVvUdTsp6f6n/fP5sRsIyGqkXGygcnLUgjZljfrPX6Z1VdX7f1UzndVN//O/1NlXf/XCRHa5RQRpKkoVzNerI4cqiKF3np8+9Xav31/Xho4eL7RJKkdyEXNnyvZ3tl/aTGuL1Nls26KZFiOQAAuBc2HnhdnSb9rlLw6Yz/yaumfq0eqF3d00/tA1XbzTkXn/CEf7/q8OczHRycJT/t2n81Htr07dM72YcxT1YCT3c+/x4T+YyXx1l9Zsr9V//0A7QUTz2vP0s/b2BSlvGTCv+GwLwy8reZ9T5R0GgI7vWbqtzvE7ZJs0/MEH4q/NNSE45c6aT8RteSqnF1ezg5d2PraN5yAABwL2w48Bpq8KfGw6eGrsIX5KEhh5K0r8N3n5gWfGFDudeSrl0Nh0Nd/feznjVXndZ99AQmMvX/1Xv/34f6xR+2Nbp4HE0GcXD288JBUHCYqSQN34/e1zpQad8/jxJl+xME159/19VQGv7uP6k4eKZ/7Evzy2io1n8VCID9ekqy/3c9O5AUEzRPhhHO2ydCgk+XRhF8sN9pV/3JYEaze57qavi73FmtJzRUMO7cHLUNv47GE2qc+sMb5y0HAAD3QeHb3Z3Z6B6vTvWs2ta1DlRtf4qZae5KJ8//0i+fXmn/6lTfVYMvTBzorPcpF0+9vtvb07e7u21nI9Hw/XP/XR/vSeEiQevV6Z5+Ghd7sMyHujr1JjzxFlV11nwXqo/h+1P9603bv7g9UPWsqfPRkLdofVbb+lXV6X0No/U+Wuzt7x+/Px+/x+Qlc6dzzUvbXy96vqXN074/c921dHB2ph8+v1H72svTr5+CT9eSyuhKJ3PeZ6u273S+/17Pym90fXDm/cD11ame/fWzPr/aX6Feovuu6tcd+pmG9bS1Sf2Fjcoisrza1q9yvDIN1HG4DkbnVODcqLb173/+pn/F9HGhtnFwoLNGU3agXc5bvoq891cAgPvpu709GbPZUCPPNh943RNcyDw0wcCrt8T7U1c62XOkuCB4eKVWvSq3ERMYgra2BpQhAGAbCLzCcjO5BnDvVRvxTx73DwO/uQYAAID76G/bzgDwMBzq/N2sxe90vrG8AAAAYNN44gWkMHxfH7//c/2m7E/AAAAAAKTDEy8ghf1Xn+jC3akAACAASURBVPTt1bZzAQAAgF3FEy8AAAAAyBiBFwAAAABkjMALAAAAADJG4AUAAAAAGSPwAgAAAICMEXgBAAAAQMYIvAAAAAAgYwReAAAAAJAxAi8AAAAAyBiBFwAAAABkjMALAAAAADL2t21nAACQve/29radBQDAA/THH39sOwu5QeAFAA/At7u7bWcBCb7b26N+tow6WA3lhyTf7e3pxx9/3HY2coOhhgAAAACQMQIvAAAAAMgYgRcAAAAAZIzACwAAAAAyRuAFAAAAABkj8AIALGZ4pdbpcz3b29N3e3v6bu+5np2+19VQGr4/VWsYXf29Tp6P1vX/nj/XyVV4xavTyDqR9Z+dXimSdHg/759HtnkfWf9qnI9np1fJ6QyvdPX+1Ft3Ko2cy0ndrKcuhro6DaTzfDr/G5OTcp3K1rrO+VB+n+vk/U6d9euXSX1f6SSmnk+uYuoxti5xHxB4AQBSG74/1bNyVW/a0g9nPfXv7vTt7pM+//y9uvU9WW/+DK1/dfpcVvWN2tdV/dq707e7O33rtXWma7Wr5dDFxeG7O33rnanq///grDdev3p9ret2VdaMi5H9V5+8tA/8D67f6F+BC8jh+79U+dTT2YF03XZiL+KH75/rX/WqfnrTVvt6lZLavDzVzTrq4uq0rJ+ClXDd1pvy840HX3kq16h1lLOuTv38jj64VvtNWSfJcdq9ll19H+r87k6/Vg/G21bbdzo/9Oqxfxb+/NunV9rfzCFjgwi8AADpXJ3KetPWtaRq+5POX+1PLgz2D3X+qT2+gJS8IMa7cD7QWe+dDvcn69qjda/fyAreid//fnq/+4f6ZXRRcv1G/5l1Qbh/qH88m1zAXL+pjy82h5L2te8v/0HFmKua/Vef9PnTnX6tTi/LtTzWzSp1cXWq/1Pbv+jt6ddJZKHPv28w8spjucasu/w5f6UTpxQIGM40SunPvx7g85YN1Pd+afSvA5UC9bH//Q+ZHBLyhcALAJDCUC2n7f3z4Ey/HMatc6hfzkYXD1f6zxv/FvrBM/1j6oLvUJXRFUzSnfil/aCzs1Hi13rz3/BV6/6rT/p2906xh7CT8lw3S9bF4Tt9fnfoX/Tu6/BVY3zB+8P3m3oOkOdyjVr2nD/U+adXfsAw1HDo6lrSQfVM/3710J637FJ9Y1cReAEA5hv+rs+joUg/fJ84BGb/1TvZ+5KuflNb89f3XMud+SJL8AIn6YIo4u/vJk+t2tXIsKngu0P34H2WvNfNWuuiqsqmIua8l2vUKuU8fK9ne2VZ1bakA6kU8xTuvttmfePBIPACAMzn3wlfp/3SZHhU3LCm6zdl70KxXNWfBweqnrXVX+C9h8OfJ8Om2tVTdf1/D9/X9VP7WtX2nX6tXqsdGJq1k3agblaui+Ff+lNStb3BJ5U7UK5RS5fz/it97vX894+udf2mGh4O+RBsqL4nQwqv5Q5HY0KvdOK0hfuPwAsAsBVDd3KZEzd8bDzRwN2dPn/6pPNXh4u9bL7/Sv8evxvUVvvz9H69CyPuRketvW5WrIur/76Rzno63/Hxobk+5/f3dfguMMlD+zc9sNBr7WLr+/BnnfkTbHiTbzzXye/SL41de7EUyyDwAgDMd/jPyUvlf/41f5rjhdbPbvjY/qumApOFeZ8F7kJ7F0bhl9x3zo7UzbJ1MXz/XP+ntj5v+p2jHSnXqFXP+f3A+3QPysbqe1/2u0/jAPvbMgE2dhaBFwAghXSzrA2vrsZTJ0/W/6z/Ra9Khu/1f+P32H9eefjY1WnS797sy25Ohl9J3oXpr9UDtat7+ql9oGq76b2zsbPyVTfrrIvh1an+o6Y+v5vkYvj+/YaexOSrXKPWUc7e70c9j7wPtq/SgaTqP+/RBDRp5Lu+cT8QeAEAUhldvElSuxr5cVD/B0f/89dk+uX9V5/G74y8qZ9qvPrwSq36G3/2tHZ49rThX0vkbKjBnxpf/AxdhafNDg2/kiRvSNU3//d5zg+jUddQgyVysU35qZv11cXw6lRWta326L0n/8/6rI09HchPuUatp5y9p1/XoWMbXv2uz9dV/fru4YUKG6nvBMO//py7DnZf4dvdndl2JnbRd3t7+nZ3t+1sAPcebW116y7D4dV7/cf5rPb15P2Fg4Oq/l8z8Ds2KdZ/1vhZdmCDq9M9/TT1fvmBznqf5j+RujrVs2pb1zrwfn9n6prxSifP/9Ivn15p/+pU31WDO5rsIz4PkqptfcvoQnSd9ZOLullHXQyjnwfWOOutfdjhvDrIRblGraOcdaWTejXw48kHOqg29O93iw19u2/9dFb1He9KJ3tVTZ8GZwtNrJJX3+3tyRhCjRECryXdt04GyCva2uoow3yjfraPOlgN5YckBF5hDDUEAAAAgIwReAEAAABAxgi8AAAAACBjBF4AAAAAkLGCJN54AwAAALB2Nzc3285CbhQMU40spVAoMEsLsAG0tdVRhvlG/WwfdbAayg9JODfCGGoIAAAAABkj8AIAAACAjBF4AQAAAEDGCLwAAAAAIGMEXgAAAACQMQIvAAAAAMgYgRcAAAAAZIzACwAAAAAyRuAFAEvpqlYoqDD1V1N321nblEFXtbJ/3OWauoPYldRt1lQuF1RbpGDmpj1Qs1aelHvi/pfZbtm0cyBFnQyaNZWDx7b1tO95nWCL0vQ/WfVRtAfEMDniOpaRZOzOtnMyX7joXONYMlLgL3AQo+OSLOO4m8/rxnRsI9nGO3KvTKx7fcDYhJx1U2OTdh3+y+M5n00ZdowtGbvjHa8bav8jrnEsy1h+2aTv2+el7RrHtk1nVNSut/70/qPSbLds2stbX/2kqJOOM14+PrZUFZNV2vmok7z2M7sin+WXpv/Jqo8yO90e1imf58b25KQ0woHL7gVevo49HVy5jrEd1xjXMdaOHNvyIgGo5Zj8XYJi1+Sz0/a+rHMYY8XKogxdx5pq4x074cJiwf5vbtodZ7rs/X3MDHzTbLds2itYV/3MrxPXOJFj8G4gzL9gyyztnNRJPvuZ3ZHr8kvT/6y7j9rx9rBOuT43tiAnQw2LqveMjOvI2nZW1qx7/lGPnxalYl09Y3RR2XaOsuTXo/H/enUVt50lIAvdczX6fTVKBRXKZZVrXQ0e1DCPrs4bfVkvnobaeOmxJbUuVxxqmSLtSl31aOdSfKQn85JOs92yaW9dmjopqh45OPdrX7KPNfurKcO073Wd4H6iPWB5OQm87quuLvV6uoFIUrcWei9kPK540FSt2VWzHLMscbtBaP1CrRtYLzymeNAMjAkulNUcxH3ubzNKo9xUs5aUfrrl8dek8e/IlJuDmeWQdAxx5TDvuKL56i58HEnv+Xjbz0svVG6RbePrLFif3r7LzUFgnWB5JJ9n3cT9NkNlWB4lFjqflt/vfdG9bE3+0++r3zpSqRQor/tucKsbSU8ehTu34qMnkm50u0oxrJS2pRdPl7ndk2a7ZdPekEXLbTBQt1bWW3XkzrsjmGXaie5BneB+oj1gFdt+5BayQ8PxYosuNNSwY+zER8qjscGjzQLD8lzHWIHhiuFH0zO2G/1/vK1rHCu8//D6o2GBk3XC+3KN44RzHx1GFH3UPm95WHT/3rFZkwOfUQ6zHtn76U69Y5d8XFGLHcco75O8RLdPTs81jh1f7x3H+7xjB4cO+MdmOcY1ozHdMpZl+evEl+n0+TJvv/Fj0Tu2ZRx3lf0uJ2/d1KifUsLfgxjqkdRXxw23nrX+OtIOLl/myyPNdsumndJa6meRcuvYgSHh9vwhs1mmHWcLdZK7fmbH5Lr81j3U8AG0h3XK9bmxBTzxWjt/+FHhSDfOSfwj5cGtbmTpccn7b+mxJfW/ypX8IYm98VMy92tfsh6rNG87SZULV47VV+NlU83aS+nDxWT/g6betiw5H0bD/4qqv7YTj2LQfKmvj2bdmfEetS+/3Jf02H1WOaxg/nFFpTyOpdIrqn4RPxyzUq+rOGjqbcvW6/EjU7/O+g2ddyu6MK4cS+o/ea1evegt/+DIUkuXXc04X+bsVxWdONEhY11d3rzQ0+Iq+70n/GHDxhgZ11XHsUNDpPuN84czq2FuDNR8K3UWvpucZrtl086xyoWMMXI7jqx+S41S5In1VtN+oHWC+4n2gAgCr7Wz5LhGpmOr3yjFDz0KBBXdWkGluAt7f6jW5XHgXam52xVV73Vk9xv6+PhDeIij+1V9PVHoyXjlQsZcRAKflo4KBb3Uhxnvow3ULF/qsZP0Rt685V5en76wpNbR7GFoceUQyWu6KbzTHNcyx7GIBdNzv6ofOsaCCkfeELebwFgG63EgHPXHed/cDtKdZwmK9deyR4GUJHUvpdfh8s9ivzunWFSlfqGecdUZ38dYcagdFtatnYdvNK1xu2XT3gXFSl29ji2pr69rvjOybNoPvU5wP9EeMELglZXKhVzHUr/xMvbuxugdm8tjIzfuQty/S3J8GQ4q5m43uJUsS/1GKSagSXNBaKtjOnqSFDTqVs2y9zTtaez285ZPFOs9GdfRzZH3hLAVt1JCOUzyamRMR7ZaOkp8lyzNcS1/HOksmZ7lyDWBCUv8v17si4PT5p4vibynXq23TQ38u2nHC/Tqy+93VxX9J87bzseGBAPtgMHtjRS9wZNx2oNmTZfHF/Hv0s6QZrtl096KZeukcqzksQ8bSDuY3n2rE9xPtAesgMArQ8X6B2/oXykSMHRrOmp5QcO8py+Vk8AQrrnbdVV7KZ30eurYUusosN/SY1lxd1oGTTWnAjTvojt2yFTro/Shl9zI5y2P5vi8ob4fFM3qkELlML1Ux7ZSDGebcVxRCx7HXMukV3osq/9RXxZ5euIP83vxtLjQeRanWH8tu9/QefOLPj6ZMxPTGve7u/ynuKsGHjvBa3P9j19CNzvSzZC3vrQHzZrOH50EzjPvh1Dn3VtJs92yaW/PKnUyGRq8+bQ997NOcD/RHrCCbb1cFuteTa4x/nBqogJvsofAhAb2ZGIC17FCxx9cd9Z205NpBCdiCK4fzl/HTpqwYjrf651cI3o84ck1ZpVDYl5HE0fMnFxj/o8Ypj6Oju197jrGmlEOqdJLmDggXMeT7b3kpidICU5kMft8mb3f8P6jy9ew3wXkrZuanG+BH7D0uY71MCbXMMak+wFl36hvjyubjh3T789PO+kHrENtKybtNNulSnuN1lc/c8rNn0zHdjrjSZY6dsw5u0ydrJB2Huokf/3Mbsl1+c3qf9Ks8wDbwzrl+tzYgtyUhndxlu+TJyh8IkV+ODh6YR+c1cbumPGFm/9n26Pl3sVqtCwmSSVvZ1nh/YYa5VTwNZ12uBH7ncc437axA9tZjjuVvjNneeRnBMfl5e0/fFyjjildXoN5jtSD3Zl7XNOTEi1wHIHZ7eKOQ3YnXXrRWfKmZhMMH2t0lkPLtifbh/I4+zybt9/xMSbU39L7XVDuOu1QuVnjL17jOsa289lvZVaGrmPsUZuLCUSNSdG3x17UzE478aJDkVklI2mn2S512mu01vqZWSedyI/c28aJr7SF62TZtPNSJ7nrZ3ZMXssvzbVlFn3UrreHdcrrubEtBWOMERZWKBRE0WG7BmqWS/r4wk39ztfiu2iq9uWpLkLpb2C/AXlsa4NuTS+PWhpPG2JZsl9/0EUln2MM81iGmKB+to86WA3lhyScG2F/23YGAOTX4It0zFu7U4qVC/XMxbazAQAAdgiTawBI0NX510dMUQsAALAGBF7ATuqqViip0Zf6jZIKM38MbTGDZtn/3bBLHU9NS5jdfgEAAO4z3vFaEmNWgc2gra2OMsw36mf7qIPVUH5IwrkRxhMvAAAAAMgYgRcAAAAAZIzACwAAAAAyVpD3o2sAAAAAsFY3NzfbzkJuMLnGknhZENgM2trqKMN8o362jzpYDeWHJJwbYQw1BAAAAICMEXgBAAAAQMYIvAAAAAAgYwReAAAAAJAxAi8AAAAAyBiBFwAAAABkjMALAAAAADJG4AUAAAAAGSPwAoCldFUrFFSY+qupu+2sAQCA3MlJ4DVQsxy8cCmrOdh2nhYRzX/4r7xbByN1a4GLR+/Ydu4YgIwNmm/Vivncck5U2XhutikYgMYFnZH+sdxUut5kwXRTfW+k2WbXv4+kbMpuiXRT1fVDqRNs06BZVqFQUG3uXbHAOT73/KU9YAlm61zjWJZx3OD/ZaTgZ/kTW3SuYyzJ2J3JRx1bRpJR8MPcG9WB/2c5JsdVgXsuF93UlGi/lW+ZlWG0z+vYRrLNpLeLllPH2Gn6w4XTTfO9kWab7XwfrbV+Mim7ZdJNU9f5qZN89jO7I7/lF76emXU6LnS9ds/bwzrl99zYju2XhusYJ3oe+ie0ldezyCSdSF7DCrer/DcKIM9y2Wl37MCNCctYdse4OW7fWZVhx56+kAh/5k6XS8eeezNnbrrLfG+k2WZL30frrJ9Myi5NusvUdY7qJJf9zA7JffnF3BgP8oKu9Ndp9709rFPuz40Ny2lpxAUw+ZI+8JrcRbE74Tsv40Yyvoib3C1xHWtyYRfTGSQtD3/upzdK33KMY0/2L7sTuYCcvzy+Wft3ciJ/luMa4zrGdjqxd5ySjzHyxM3uzD2ufHY3WIc8dtode/p8D7XpnMmmDBP66ak7v9HF8/r25dJd7nsjzTbZfx+tr36yKrus6nqZvKRdZzF57Gd2Se7Lb1bg5V9LpD+f7n97WKfcnxsblpN3vCIGt7qxHJ3cixclBrq9kSRLj0tF1Xsd2ZJkd9SrF71VKhfq2JYc90IVSd1aQaWPL+QaI2NcOVZfjdJk/PCs5cV6T65jSbLVMReqaKDm7bGMMTK9uuoXRh3b27+5qEiVC299y5GbYnkx5via5SO1ZKtjjIzxjs9y3PHx3TTeSh+MjDFyHUuto7i89lQfJ15UvefKW+TlY95xTecLyMigqbdxL3dJ6jdKD+d9yMGtbhIX3ug2phi6tYIuj40uZvXtS6Q73m7R74002+zS91FWZZdVXS+Tl7TrAKkM1HzbkixHjy9Tvo9Fe8AKchl4dc8/6sWH+3ExPWi+VKMvyX7tBxYVnTiW1LoMvIjZ1eXNCz0tyr+os+SMj7+o+ms7mODs5TH7//poVmvs6rzRX2G5zz6On1CgWFcvEFS5X/uS9Vil+SnONP+4gIwU6+p5owVkXFcdx5YVWNxvnD+gWQ0tPU7RmEcvth+1pNZRQYW5b7inSzdome+NNNvs3vdRVmWXVV0vnpfdqxPk1uCLPvYl68lX6XjUrzuy+g2VZp67tAcsJ3+BV7emy+Pg04/d0zqa3DUpNfqTp0e+Yv21bLV0OX6EdSm99huN+1V9PdGj4PFXLmSM9zRs7vJJLnRUKOilPsy4wzJQs3ypx4615HJJKurpC0tqHc2eLahbU6Hg3fGZfkLl5TXdVNxpjgvYkGJRlfqFesb1nhRLmvlk4YEq1nveBY3/RFytt+udhWuZ740029yD76O51nyMK9U1dYKtsPTi5EL10TVFsa4PjrWWfor2gKh8BV6DpsqXxzt/QW13/Lsmo7+pA/KeerXeNjXQQM230nFolXkXbmku7Gx1TEdPEoc+3apZfil9uNDT2O3nLZ8o1nsyrqObo4IKhaPYKba94NDo+DIuuAoOU2zpaOaUq/OOC9iGoioX/vDYh6L4SE/U11c3/PHg9kaK3hwaq+jCdWTFbLd0ust8b6TZZhe/j7Iqu6zqetG87GKdYCcVHz2ZtZD2gKXlJ/AaNOVd5wfOoG7z3v42QbH+Wna/ofPmF318EhimV3oc3zAHTTW7KZaHeAFe7NCn1kfpw4y7JPOWR3TPG+r7QVHywEepcuLICj7ti+T32JbU/6rZ/dKM4wK2xn/6m/jFe9947bUVaczu137y0GPJv2iZNUxngXSX+d5Is83Ofh9lVXZZ1fUCednZOkGuFZ/qhdXXxy9xJ1JyEEV7wNK2M6dHhD/bjKJ/OZ6tLrboFpzSM2n60rjPO/Zkppx5y70ZAEf/n/7tiOg0qK5jhcp63vLpw7YC+fH2NyoD17FCM+2E103Iq+UYdzSzYTQfM44L91NeuqmJ0Xlqm07MbKN5nNkwszJ0HWMF+6K5s+d5/cvcMkqT7jLfG2m22cL30VrrJ9Oyy6qut18n+etndkvuy2+hWQ1TzBJ4z9vDOuX+3Niw7ZdGcLryHZma2ZjoiRSZ/jxhCvgprmOshIYSna46aYr66PKZ067LNrYdLt/Q+pHp5OOWh/M6OW5v/+Fp5Uf1ly6vwTwvOJ38nM4Ouy13nXboS88ydmd8F8HY9gP84guVR6QtxvTv0xczo35jVnAwP93p741Iumm22dL30drrZ91lt2S6c+s6R3WSu35mx+S5/KZ+/iPuuitynoXP3YfXHtYpz+fGNhSMMUZYWKFQ0MpFN2iq9uWpLngrEki0lra2ZoNuTS+PWhrP92lZsl9/0EUln205j2WICepn+6iD1VB+SMK5EUbgtaR1nEiDZlNuvZ48HhgAnfYaUIb5Rv1sH3WwGsoPSTg3wvIzucaD09X510cEXQAAAMADQOC1YaMf0ysULnXMHKAAAADAg8BQwyXx6BTYDNra6ijDfKN+to86WA3lhyScG2E88QIAAACAjBF4AQAAAEDGCLwAAAAAIGMFeT+8BgAAAABrdXNzs+0s5AaTayyJlwWBzaCtrY4yzDfqZ/uog9VQfkjCuRHGUEMAAAAAyBiBFwAAAABkjMALAAAAADJG4AUAAAAAGSPwAgAAAICMEXgBAAAAQMYIvAAAAAAgYwReAAAAAJAxAi8AWEpXtUJBham/mrrbzhoAAMidnAReAzXLgQuXclODbWdpIZH8R/7Kzd06GgDzDZpv1Yr53HJOVNl4brYpGIDODzq7tYIKtTSh6bx0o/1uWfO72jTbLJNu/gyaZRUKBc0q6jTrhC1YJ6m+yx9OnWB70pzr3dqi1260BywuB4HXQM3yS+mDkTFGxnRk9xsqpf8myIGi6j0j4zqyJNmd0bEYdWyp3yilvNAAsBsG+vJRctxJWx/99erFbWducwZNlQtH0qjP60hHM4KvQbOso7hodeF0o98brhyrr0Zp1gVImm2WSTdvvIuyUqO/4jrRTRatkzTf5Q+lTrA9Kc/1QVNvQ32TpRdPZ/TltAcsy2yda1w38lHHNrIcE/04T+KLrmNsydid4GeucSwZyTJOng8IyKlcdFNRHdtI8v4sy1h2Z7ofy5GsyrBjyyjc4cV+ZowxxnWMZdnGthKWL5Ku6xgnmoTrGEsyVlJHm2abZdJdg0zqx8/3zKJOs45vfl0v8V2eozrJZT+zQ3JffnPO9Y692DXafW8P65T7c2PDclkaHTvdF8E2pQ+8/MYoGbszCsK8v3EjGV/E2WbcZB1rcmEXE7QlLQ9/7qc3Sn/U4IMXjVP59Y5Bkb/4Bh2/ruR1PqPjHv0/fLHqGMdO3jb+OCflM9q35biBdSLllHCcncT9OinqZ/n9Yjl57LSTzqGH9cUX399553+wrY7WtU1ndCNqZqNYJN0U2y1zDCunu5j8B17L1cly3+XbqZM89jO7JPflN+tc95dFrz+S3f/2sE65Pzc2LAdDDcO6tYIuj40u7s1LEgPd3kiSpcelouq9jmxJsjuTIUmVC3VsS457oYq8Mih9fCE39Bh58gh71vJivSfXsSTZ6pgLVTRQ8/bYeyTdq6uormpHrfFwyI4ttd6Oxh0P1CwfqSVbndGjcUmW4yYMn6rownRkj9f30pPdkbmoqHIR/r8qF17eLEdu76kkxzsG15Elazxsq/P4VgP/OF/qQ+BxektH5aYG6qpWOPLer/n40l8nWk5JxznQbeJ+pacz6+dYl0vvF/fG1JCUiX6j9HDe6Rzc6iZx4Y1uA8XQrb3VY79/W2e6U9tZjk4W+e5Is80y6d43S9TJ0t/l1Ak2rHve0HggYuto/jtTtAesIDeB1+jFx6OW1DpK+/J1/g2aL9XoS7Jfy7uOr+jEsaTWZWAscFeXNy/0tCj/os6S86Eu77K/qPprO5jg7OUx+//6KNAaB7e6kaXHJe+/pceW1P8qN7iRfZzR5ABdnY/HWRdVvxgdQ1ilXldx0NTblq3X44DPP85+Q+fdii6MK8eS+k9e+wFSUfUPjiy1dNmddZxz9juzflbZL+6NYl290TtdrquOY8sKLO43zh/QrIaTcz3JoFnW5XFPi736Nj/dqO75R734EN+2V9lmmXTvp3R1sup3OXWCTatcBN7T7diSwje749EesJzcBF7Fem/yAqIktd7u7IuCraPJbDOlRn/yxMdXrL+WPbpQl6TupfTabzTuV/X1RI+CLahyIWP8u8Xzlk9yoaOC98QodIelWFfPeBdB3Vr0hdOinr6wpNbRArNcpTVQs3ypx441f1XJP07vGMYz9/hv5d8EbidZwZ6v+EhPRstnHudsM+snw/1iBxWLqtQv1DOu93RX0synMg/NoKnzaB+UhW5t8eAuzTbLpPvArfRdTp1g2yoX/miYwDXACmgPiMpN4DVR0YXryFJfX3f0MUFwVkNjTCjo8nhPVUZD35pvpePQKvMu3NJc2NnqmI6exAx9Gk2Zenls/GGJE8V6T8Z1dHNUUGE0rG5lt/4sPBd6ushmlj8kcMlZ42Yd52zz6ier/WJ3FVW58J6GPhjFR3oS008Pbm8k/+ZQ97yhVqMUmPa45I0AaB0lT+2cIt3wgqbKl8eLBXdptlkm3ftq0TqRtPB3OXWCvCjW9doO3+QNL6c9YHk5DLzkn9SLDzXZJcX6a9n9hs6bX/TxSWBoX+lxfMMcNNXsplge4gUQoaFP3ZqOWt47WUmN1Rvv7AVuyYMYF9D6KH1Y8I5M6bGs/kd9WeTJgT/M78XTYqrjnCWxfjLeL3aZ/8Q48Yv3vqno2JZakdvC7tf+eLhyaAjP+F1NeaMAEtvI/HTHBk1593QCn3abc97Pw2eQPwAAIABJREFUSLHNMuneawvUSVDa73LqBLky0O3NrOnkaQ9Ywcam8VhAx87v7GAjsUW34JSe3sxo0zMWxn3esScz5cxb7s22N/q/P/OgP92Nt2yyrZdWdNvR8skMfjGZ92ZJdB1jBaZHjU6xGv2/61jT06l27BnlEJ4hyHUsf+ae0QyRkXLx0553nLP2G95/dPka9ouF5K+b8tuUZZtOzGyjeey7MitD1zFWsI3MnXkwzayGKdMNzkQW/JszXfPcbZZJd0WZ1M+ap5NfvK5TfpfnpE7y18/sltyX34I/nZDuvL2/7WGdcn9ubNj2SyMy9bZyPCVmUPhECk8Tr7gpxuNEgpag6HTVSVPUR5fPnE4+MB36eDs7qfzD6011FoGGH7d+dDr58PTrgQ4i2oHE/S5GbD68Mrdse7J9qCyTjtOvlzn7Ta6fFfeLheWu0w6dO5axR9GX6xjbfoBffKHymHeTIS7wGrWZWYFV3E2TeVP6R9JNs02qdNdv3fUz9XMHMd8zs9dZT51Md6v5rZPc9TM7Js/lN/tcn75+m3vejje9v+1hnfJ8bmxDwRhjhIUVCgWtXHSDpmpfnuqCtyKXMFCzXNLHF0lT3a9jF3H1s4H9ImQtbW3NBt2aXh61JlMQW5bs1x90UcnnOZHHMsQE9bN91MFqKD8k4dwI+9u2M/CQDb5Ix1y85xb1gyTFyoV65mLb2QAAADskn5NrPAhdnX99lNHvZWF11A8AAADWh8Brw0Y/plcoXOqYae+W1FXNn5a63yit9ce2Z9dPdvsFAADA/cY7XktizCqwGbS11VGG+Ub9bB91sBrKD0k4N8J44gUAAAAAGSPwAgAAAICMEXgBAAAAQMYK8n54DQAAAADW6ubmZttZyA0m11gSLwsCm0FbWx1lmG/Uz/ZRB6uh/JCEcyOMoYYAAAAAkDECLwAAAADIGIEXAAAAAGSMwAsAAAAAMkbgBQAAAAAZI/ACAAAAgIwReAEAAABAxgi8AAAAACBjBF4AAAAAkDECLwAAAADIGIEXAAAAAGSMwAsAAAAAMkbgBQAAAAAZI/ACgKV0VSsUVJj6q6m77awBAIDcyWXg1a0VVKjt+KXLoKlyoaBcHka3Frg4HKhZLqjcHDyc/QNrMGi+VSvmc8s5UWXjudmuQbOswsz+Lhikpg1M523j9R2TgLes+d1Imm2WSTdvFiy7clPpDjGLdB9KnWCbctFH0R4gSSZnXMcykozszrazMtO8ouvYyvFxuMax/PxJRpZj3Ae1f+ySHHZTxjuHLePsyImbXRmG23Jsd+c6xgou69hGss3MnnHuNtHyH+VjVp2k2WaZdFe31vpZuOw6xk7zXZVJuvmpk3z2M7sjv+WXlz5qt9rDOuX33NiOfJWG6xjLso1t5TVgmZh9InWMLds4jjW/8QKYKZeddscO3DiwjGV3jJvTLz1jNlCG0YuQgI493Z/HfbbQNq5jnOjmfh6spKuPNNssk+4arLN+5pe3O32uduy5N8AySTdHdZLLfmaH5L78Nt1H7Xh7WKfcnxsblqPS8IKVzih63+HAy3UsL/8JDX38NMy/+zF+yuc//ekE/6/wuuO7JgnLo2mHLxAd48xZ7gaPYZz25E5K+HM/qBylkSL9tPuPlFjsMVuOa4zrGNvpxN7RSjqGqSdu0TqIOa58dmcPQx477VA7i56TObS9wMtru1Ofz7yjvMw2M7abKc02y6S7mPXVz3Jl17GXLIOV011gXwuvs5g89jO7JPfll4M+apfawzrl/tzYsNyURsceXRjveuAVfAyc/Gg5erfEdayYwCfy2NoeLR8FqfFpzUs71fLx/0dBymR/4by5xoncfll1/2HR/XtlGrz7Y00Fhkl5jUk3mo8Zx4XtyF2n7X+Bx978yGnwtbXAK+nzjp08NGaZbUbbLXqTJM02y6S7oLXVzxJll+piMKt0k/a1hTrJXT+zY3Jfflvuo3atPaxT7s+NDcvF5BqDZlmXxz3Vi9vOyRp0z9XQCz0tSlJFx7ak1uUaZjkrqn5R1+JF1NV5o59++aCpty1LzofRvoqqv7YTtx40X+rro1lTCSy4/yT2cfyEBcW6emZy7rhf+5L1WKX5Kc40/7jwYBXr6nk3rWRcVx3HlhVY3G+cM6thiKXHCzfIxbfpnn/Uiw+L9ZFptlkm3e1KV3ajyQaOWlLrKM2EVlmlG3Y/6wT5ll0fRXtA1PYDr0FT5/qgi3tyjdu9bMl+PWkAFS/y0mVcW2sdjWelKaUJPhY2ULN8qceOlX65+1V9PdGjYAuuXMiYi0jg09JRoaCXM+tuif1PKerpC0tqHc2eIbJbU6FQ0OWxkelFOyAvr+lmK0pzXICvWFSlfqGecdUZ35+40S0zTG1Wt7b4zbs02yyT7o4o1nvezQPTkS1JrbdrmRltpXQfeJ3g/qE9IGrrgVf3vKFWoxSYFrOkRl/joCSX07EnGTT1dnRXY3Q8R96E0624yMvu+A3SyJ0ZfCzjVs3yS+nDhZ4uvDzNhaOtjunoSaOUMBX8KvsPK9Z7Mq6jm6OCCoWj2Cm8veDQ6PgyLriy1Rl3fC0dzZzSdd5xAXGKqly4Wnsz3nXFR3qivr664Y8HtzdS9AbPstsMmipfHi92oyTNNsuku23LlLcqunAdWTHbZZ5uKLF7WifIt030UZJoDxjZeuBVuTDj4MP78y9e/KBkl06owZePkuNGjsd4d8LXMtxwAa2P0ocZd0GSlpcex3cMg6aaUwdQ0YljxQ+tWnb/CbrnDfX9oCh54KNUOXFkJT1hHA397H/V7H5vxnEBifyns4lfvA+R1+aiN57cr/3k4cOLbDNoyrt/E/i025x9RznNNsukmwvLlLf8C8lZQ6eyStd3r+sE+ZZxHxVEe4CUxzfednRyDdcxVtJsNqOX8ReYACN2UojRVKSRFykzmVwj8oJox06asGJ6ApH1Tq4x2l94wpLRBAauY4VeWA2vm5BXyzHu3Mk1Uv62DTKXv25qdB7ZphM5aV3HYnKN2GWB/iT1b+TM2SZpkpM50zXP3WaZdFe01vpZorw7dopJYTJNd/t1kr9+Zrfkvvy20UdF7FJ7WKfcnxsblsPS2MXAKzjdeWRGm2gDiZlSffZ08oGGHEjLK57INOuR6eQtx51K25mzPBx8zZuiPTLtumxjr2n//t7G077HHe+oA0uX12CeF5xOnt9i26rcddqhNm0ZuzOO8o1tP7wvvqmp9eO+/ENlFm1Po3Y9K7CKuQkVd+Gh4IVNJN0026RKd/3WXj8Lll3SFNur1sncdHNUJ7nrZ3ZMnssvL33ULrWHdcrzubENBWOMERZWKBRE0QHZy2NbG3RrennU0nhKHMuS/fqDLir5HGOYxzLEBPWzfdTBaig/JOHcCCPwWhInErAZtLXVUYb5Rv1sH3WwGsoPSTg3wrY+uQYAAAAA3HcEXgAAAACQMQIvAAAAAMgYgRcAAAAAZIzACwAAAAAyRuAFAAAAABkj8AIAAACAjBF4AQAAAEDGCLwAAAAAIGMEXgAAAACQMQIvAAAAAMhYQZLZdiYAAAAA3D83NzfbzkJuFIwxBF5LKBQKouiA7NHWVkcZ5hv1s33UwWooPyTh3AhjqCEAAAAAZIzACwAAAAAyRuAFAAAAABkj8AIAAACAjBF4AQAAAEDGCLwAAAAAIGMEXgAAAACQMQIvAAAAAMgYgRcALKWrWqGgwtRfTd1tZw0AAOROrgKvbi18AVNuDradpSUN1CxHLsbKTe3q0WxFtxa4gPXKc3fPB9xHg+ZbtWI+t5wTVTaem+0aNMsqFAqqJUacwSA1bWA6b5toP1vW/C4izTbLpAsgz+b3Uctcgy7YR6W6DqSPuu/yE3gNmnobuoqx9OJpcVu5WVFR9Z6R6diSJLtjZHp17erRbEXlRI7V0lGhoEKhpIYcfahTgsiLgb58lBzXyJjwX+9BnafeBUCp0Z+xSlPlwpHU8cuoIx3NC77mbjNQs/xS+jAqd1eO1VejNOsCJM02y6QLIL9S9FHS4tegC/dRHdn9hkqzIj/6qIfB5ETHtozjbjsX6SUVnetYRlLin93ZcEaBHZejbmqiY0/atWUZy+4YN8f9V+Zl6DrGSujfOraMIgviPltoG9cxTnRzPw9W0hdJmm2WSXcNcnmOPzDUwWpyX34z+ihjFr8Gnd+vudPfCR3byHJM4m5y3EetIvfnxoblozT8k0aa/WWcJ9MnkmscS0YKNN6OHf7/6DjHDa9jbL+xTAK2SOMPXuAFOo2OHQjo7E444LMc48xcbhvbmiwfN9bxvmzTcR1jOx3/mOKDxnCQOcl3+HPbdIJpx+QtfBE7f3l81+KVZTTQtRzXmBnHknQMk/pMKMOY48pnl7f78thph9pf9HzLoe0FXl67nPq8Y0/a0JRltpmx3Uxptlkm3cXk8Rx/aKiD1eS+/GYFXgtfgy7XR3XsZfqRfPRRq8j9ubFhuSiN6YuY/D/9mjqRokFW0mfjxj8JFCzL8i/YRhf7o4YbbkwdO3yBH73j4jrWAsv9/U/dsfHz6zrGmgqmJh1KOC/RfEfXd43jRPezSt6j4ssteIdo1rFE/z+VbjQfM44L65e7Tjv4Jb0jwdfWAq+kz+P6xlW2GW236A2QNNssk+6CcneOP0DUwWpyX37znsovcg26RB+1XNBlctNHrSL358aG5eIdr8pF4B2Jji2pr0Zpt2YGG9zeSHqiR/Ne7yg+0hNJN7clXRhXjiX1n7z23wspqv7BkaWWLruSBre6kaXHJW/T0mNL6n+Vu5YcV3TiWFLrMlDOXV3evNDToqRiXT3T0+h1FfdrX7IeqyT5Y6EtOR9G760VVX9tJ+5p0Hypr49mTTfQ1fnM8dfzlvvs4/hJDWYdywrmHxfupWJdvVF/5brqOLaswOJ+43yn+q7sTfqwLLfpnn/Uiw+LvUubZptl0gWwO5a7Bk3XR40m9ThqSa2jggoz3/GaRh91/+Qi8AqpXMi4geBjRxSfvpClG93Oe7nRD6aCL21awdY7DswGoYChW0t4ObR1NJ7ZZu7Lo9E811/LDpZz91J6HWm83ZoKhYIujwMThLhf1Y8GmZULGfP/t3fHyuk6//7HX/7neyO/M/op8s0VYH/OaBqrtOmw1JnfSZcyXU4BpXRpU9kE5lyAXoHfFIE5t7L/AomAoIiiaJ6PGWc+H2XXdRc2vGHZneUCn3hyjCe9a1Yan0Ry+3PdOVbNzyWpq4dHS/KGO2csKvwtubJWm3Wtyu/Cr9DtajCZaWFC+T/XHir0AzitYKz5aHNx5WRp6uQL4Hqd+By0O1lsJteQJO+1+iQY9FE3qX2BlyR1J3qx18HHtehO9GLvmVkmctXvTbW0XyofJMn0pvORUVgUfNj+z5Waws93iu96ea+uIkVyX6VRPpAYzGSM0WieD0iqnFza8o2v+2mvZFrW7/XsPDM9FKbf9/lGd7KQCR2thh11OsPCab7Lf0tS1qRz9DTcOe3rvt+F36erwSy+g42U7h/da6mv3G36nSMEDk0TuerPR4ddBKmSpk6+AK7fvnPQOv2aBpqFjqyCdIXoo25WOwMvRfpeXd908oOZkfHvNe2t75wMPcW3rNf/70117xuZXUdJ+o5YMNbQiwOCpg6s7uRF9nKqN/dTH/clQ/UkDZ5TV4B6d8WdR+TK3bpCFAd3hcOvvA/pfceVmn2f5wRvUy3XQVH5wMfcb9n+VCNbFYZ07vhd+KXWd16rDDn+NeLjycsdbOHXsnxo8CFpIlfxtZnUu4G7+4pylTR18gVwI/adg9bp17QO2CoMUaSPummtDLyCcU8fj+/Xeet0fVdlM1Z4vY7X+r2iACp98h68TbW04ues4qsnmztL4ddhQwkLbQUU6w5k+qHH503hIrefGbYXfX5omXQY66tB3jB7dy94+1LRI0/JkMZhfhzgvjt/B9wZjNy+hp4lJ8wPd9zzW7YEmnuq9AxY6e/CjVsvmtkfKyj4I/cbF1DeZfDsyEoPr0kuKO24mlQpTTKCYDlVL71Y/atUer5UJU2dfAHcjCrnoHX6tWA81MrZc25LH3X7LjGjR1Zu2u4WT4mZtrvqtn9T8Yx88XaWbW9mSctsl50i3bbtnxl3rF1TneenZM+/tueFL5wRJz/TTz5Z2ec7p12XbexUuuxU+ttlL/o8W85NXcffn62zZIa5amVNl/nA6eR3TnONY7Sim0rLzGpoGdvfzJ5p2+2cWarJOtyaEayor8vUWf5YSY7Z3Pu70uSW2VDBMb+Vb5U0lfI9vdbt478QbXCcNtff7j6qyjnoafqovfm2uI86Rpv3jUvoGGNMWVCGcp1OR8dXXSS339PHY7ie1fAMktvT6cklIlfjzwfNrvIWI27daY6104qCsZ6Gnn7uQVuW7Jd3zQbtPIbaWIfYoH0ujzY4DvWHMuwbWX9dugA4s+5EL49u5q3oUxoRdAGVdQczLczs0sUAAABXhMDrFxpMJqn/BXr7+iNOIQEAAIDmtHJyjd8h0LjT03QpLae9gxfVO1ayqF+nM9eIuUgBAACARvGMV02MWQXOg2PteNRhu9E+l0cbHIf6Qxn2jSzueAEAAABAwwi8AAAAAKBhBF4AAAAA0LCO4oXXAAAAAOCkVqvVpYvQGkyuURMPCwLnwbF2POqw3Wify6MNjkP9oQz7RhZDDQEAAACgYQReAAAAANAwAi8AAAAAaBiBFwAAAAA0jMALAAAAABpG4AUAAAAADSPwAgAAAICGEXgBAAAAQMMIvABgS6Bxp6PO1musoHD7SG6/aPuOOn1X0ZlLDwAA2ofACwByIvdVXsH7lvOsQWGKriYLIxM6sjZbywmNzGKibkPlvLx8wNmXm48yg3FxQFoaxP4kTAW/5dtGbl+dTkfj3ZlVL2+lbdqvSr0cVnfS/japU3fX2CZ76qGxfT5XD5Uu6lxj/Z5e9X091QZ765f2wuEIvAAgI9Lnh+KgyWRfi8nthlCHi+T2n6T3pH5COdZS0172JCCYF4WwkuxRSRArKXLV7wwlf523Lw23Tmzik4/edHnC8lb7Te1WpV4OrTtVaJM6dXeFbVJh32xmn8/Xgy97OVVvZyRxhfV7ctX39WDcUaczlGf7cV3sumhGe6Eug1qoOuA8zn6s+baRFL8sy1i2b8KwYtrQMVaSVpZxqqZrWCN1GDrG8bffsyRjJT+8aBtjTOhYxi54P+HbMsptUPRe+jt35XdUefPbNKCp9tlbL1XrzlRokzp116I2qdoGterBnGKfD7f7Id82shxTWgtnrN/WnxPt2dd9+7A++9rb65xav2+cGbVREzsScB7nPtbiP8Dbr0p/1H5T4FXIN/beE3nf2LJN+SYlefi2UVG6A4KH+uWtm3817Q+8DmyTfenqfNfR+e5WrQ2OqYcT7vM/H9epg2bqt/XnRLv29fXFtuq/9/rb65xav2+cGUMNASARuXotGSW0nPbUZyzHbtG3Vpaj59LxVJKCuValz8qt8yhNvNL3KZugSnmrbHPr6rZJnbprc5vUrYcG9vlg3NF8ZDQ7tA7aXL8XEcl99STL0d284vNYtBeOQOAFAInuRIvkma4wlO/YqckypOX0bc/D8b9b8Pahx/fdk4kE85UeH/Y9K2fprnfKkpWUpUp5K2zzOxzeJnXqrv1tUqMeTrjPJ5NEDD3JG3bUqT4zSlyW1tfvmUWf+lhK1v2XNEr6fkfW3uexaC/UQ+AFAEW6XQ0mMy1MKN9O3jzxHZdbEow1Hy20e/6RQPPVo/aeg55DlfJW+k0oVKfubrJNTrvPdyeLzWQNkuS9Vp9U4Sbr9xQsPT7PNEnuGHUnenesw+q2BO2FPAIvANipq8EslGPt37KqyHVv685Z5Ko/H+0dRhO5r1o9Puy+Mtv9o3st9RXm0n6vJN3rzylOMKqUt+Jv+hUObZM6dXcNbVJj32xunx9oFjqyCtIVuob6bZHun/tdH9JeqI3ACwD26urh0dJpTvwDvX1IZxhJdx6Rq/6T9J7+6x+4hWvPfH6owpCrgUa25M2zoWn4tdw9Hfcpy1v5N/0WB7RJnbq7mjY5dN9seJ/v/tF9lSFvV1O/F9B90KO11Mdn0Q8tD6JoL9R22bk9rhdVB5zHeY+1eHYoWbbxczMSho61f2bDKrMa7ptSuAGN1WHm96ZeRb8vdIxV9XeHjrHS9bdrtrBDZjWsUt5DftOJNNI+J55OvlKb1Km7lrRJ5TY4dN9sYp//2aTCbKtnqt/WnxMdNKthhVkCr7y9zqn1+8aZURs1sSMB53HWYy0XONn+Zu0U267wR20rfe5j344/P/O8v43UYXq9swpT75dPpbwOdneexBef0GxN/Z858cjlW6W8B/6mUzl1++yulyrb1GiTSnXX3jY5qA0q7JvGnHifL6iH7bwvV79tPieqcjzk6yFbt7fXXufU5n3jEjrGGCMcrNPpiKoDmnfuYy0Kxnoaelomb1iW7Jd3zQa7hgtFcvs9TZc7NkmzfZkzDsynv2o32ufyaIPjUH8ow76RReBVEzsScB4ca8ejDtuN9rk82uA41B/KsG9kMbkGAAAAADSshYFXoHGVlcNbJZLbT614vmeBvGBccXV0AAAAADehVYFXHJAM5dl+vODc4lpW4u5qsjAyySqruxbIi1y9evE/bf+afiMAAACAuloTeAXjjoaeJSc0Z33o/KR6d7JtW5aWmr4V3/WKPj8k25ZVZS0HAAAAADehHYFXMNbQk2x/ocm13/65e9aLrZK7XoHepvd6eb7bTheMN8MPOx0loxUzwxI7xcMZI7ef+mysoCDPfq4w6TQ/WdUoQ+azcZDNo+8qKCpbsk0yzLLkewEAAIBb8delCyBFcl89yXJ0N++oM1y/bTkKr3QY3uDZkeVNNX0LNEndvYvcV62cd830qddMikDjoSfbN5oN1nf/Xl09Dx70LUehmagbuer3PvQYxsFp4LqKNFA47uj1LpQxXSVTWg/7d3HdDWYyvtQZelp+fCqaJPUZ6fNLsiTdr7+zbhl6EyNfHQ2VTI89UOis1Pt4XLffRKH66k3v5ZuZBorkfo9kzGzPb7/OtgeAQ/zHf/+X/vXv/9R//Pd/Xboov1rSBv/3P/976aIAuGGXD7yiT30sJcv+kkZGZiYpctXvTdUb/7nOYYfdiV7sqYbeq9znwfou3vpul+lqazaN6FsrWXpcDz3s3VmS96VQE01mk8KvGEwmUuTqybPjPOMv1uTF1nQ41VswUVJ1lm1LXuq96FNfd4+6V2rRobplkBRm3g30Nl1K1mNhmsh90tefRYXvFYEXfnQ6nUsX4epRh+30r3//56WLgBSOk/qoO5T5559/Ll2E1rh84CVJsvT4PNsMM+xO9O58qDdNBy7XJbnr9fEZaTLpSsFcnj3SrGjj7kQLEwcx8bNuknS//0vCLy3ladjxtj5afUdSsuDr3bNebE/DeaDZYKDo80t3DyN9TU9QhoxIbn+uO8eSPvKfxeW0nFCLdCx9ku/FrWMNkOOwjkp7JXe6uNNyWUk7cJzUQx+DMp1OR3///feli9Ea7XjGq0D3z5WffHcnerGl5fRNgSK5rys5z+V375JnpeYjo9Cxqn+P5Sg0Jp4FMvVa5KLVwciWvLkCBXr7uNNDQTBbuwySpG+5/SfpfaaHws9t+cbX/bS39bzZcd8LAAAAtN/lA6/ugx6tpT4+i+Zfv9efK7zblRg8O7Lk6bX/pOn9S/mdu2CsoWfLN0YHjazs3clafqiw6rYKM5ItT6/9V60eH7aH8dUtQ8L7kN73TY4y0LNjrYPRE30vAAAAcAUuH3itn0taTnup2eySCRdmuqpz8fBL3lfqiafkrtdS2btd4ZeWWirZNPpeSVrpO0o+Tj17lUmT053oxV5q2kvNZKh4xsLtmQEHGtnScnmvl4LoqHYZEvaOwDJT5BfZ8jRcF7DS9wIAAADXzrSFbxtJPy/bv3SBdstWXWgcS6nyW8YJk48cY/38mPx2MrIcExrf2OnfbtvZfELHWOk0ucrx7WyeVvLlqTq1/XRZct/nm+33KpYh/d2WE5rQsTK/zU//X7bxM+Wyjb/ve/HrtambulbUYXv969//af717/+8dDF+PdrhOPQxKMO+kdUxhqch6+BBUuA8ONaORx22F5NrtAPtcBz6GJRh38hqwVBDAAAAALhtBF4AAAAA0DACLwAAAABoGIEXgCsWaNyJ14HLvrIzfWZSjAu277sqXpUhkts/ZPtTlrXou/vKLYO3/Xu2pzQFAAAtQOAF4GpF7qu8gvct57l0KYrBzMgYX3Z6re6y9fCiT33I0mZTS7ZvZBaT7bXwTl7WriYLIxP6sjcF3Vo+YjBbb2PZ8kMjc9YF8fLB4XZgqGBcEGzuDo7XCVOBavm2kdtXp9MpWEKjZnkrbdN+h9RLMK4asO9rkzp1d51tsr9+q+2/h6XJ1UOlC0DXWb+nVuV4yF/E6u+tBNoLhyPwAnClIn1+SE5oZEz2tdi7qFxPd/d2KvgqXsQ9+vyQHh91n3rvrnfmsnZ7uksHifI0zP8B7/Z0d3+n3lkXnI/k9p+k9+S3hHKspaa97ElAMC8KNyXZo/J1GiNX/c5Q8td5+9Jw68QmPvnoTauu/VelvNV+U7sdVi+R29ewpIlyG+5pkzp1d41tUqF+K+2/h6bJ14MvezlVb2fAfI31e2oVj4fI1WvmOLD0+LCjQ6W9UFfzM9bfJqoOOI/SYy299p9lGcv2TVh57bfQOHZunTnLMdnkvrFlGSdMrzVXc325E5Q1zK11mF3Pb71NSQ6N9FehY5z8eovr9f5+1hIs2sYYEzrWzrUafbtkvcKiROvv3Lv2Y93y5rc5scbWj6pSL6FjLMs2tlVStyl726RO3bWoTQ5uhx31e9D+WzlNuN1n+HZBv5Ut47nqt/XnRHuOB98+rG+/9vY6p9bvG2dGbdTEjgScR9mxll84PHlV++OTBCpFi4n/fMEg6wJ8AAAgAElEQVT6j+jxgddpymqyC5Rn0l8g8CoU19Xuc3jf2Mli6ofk4dubRdjTqgZeR5W3bv77XS7wStohNM7ewOvANtmXbqfLtMnpAq86dVWvfn27Th00U7+tPyfadTysP9u+oFXm+tvrnFq/b5wZQw0BXJ+tYSEby2mvwtj8xECjzQNU8uabYSDB3JM9OsHzUicrq9SdLOSnyruc9io+23Qm0bdWlqPnXdUWzLXa8Qyeom+tShOv9H3K4TRVyltlmysUjF91F87K2yGtbpvUqbtrb5M6dVUjTTDuaD4yOviRzmuv3wYEb1P9DET0hvufmaK9cAQCLwDXpzvRInlOKgzlO7Yyc2VM3yo+zC4Nnp1NWm++Thdo7tk6Rdx1yrJK0mAWykll4A3bM7Y/ePvQ4/vuiUeC+Wr3sxOSJKvms3SHqVTeCttcm8jtaz5aaO+jkBmHt0mduruNNqmz/1ZLk0wSMfQkb3j4LKa3Ub+nFU+4lDyrZatoEqNttBfqIfACcN26XQ0mMy1MmLobdMCdke6DHjeRl+aB9t+VuVRZ40w0WeRmOnx609cJi1lLMK5wMh9ovnrU3rjrHKqUt9JvujKRqze9H37l/VB16u63tskBupPFZrIGSfJeq194oX73G8xkQkdW8rfgSLQX8gi8ANyI7tbdoKrpHjaRl7zXscavVe7KHKNuWRMDzcLUnbqlJ6987EvzIlf9+WjvyXzkvmr1+LD7ymz3j+611FeYS/u9knSvP6dolirlrfibrk3wNpU37aWmou5putR6iFXJdNuHtkmduruVNqmz/9ba55M+YDtdoVup33PoTvRiS6uyK2K0F45A4AXghiRB1GEn6N3Jy+YO0tKTp3PclalX1k3yiRbpB74uJXLVf5Le03/9A7dw7ZnPD1UIaOPn7rzc5ebwa7l7CvpTlrfyb7o+mWFVP9NRS7J9GVP2DMoBbVKn7m6qTersvzX3+e4f3VcZ8nZT9XsOkb5Xu6aTp71whEvN6nHtqDrgPIqPtfVMg5Zt/NxUfqFjVZgtcHsWwPTMg9nZocpmNQyNY8ezDFo7ZhRsoqz5PFQ4Hf5GY/1Vejaw9KuoLKFjrF1TKW/lm6rrXbOFHTKrYZXyHvKbTuCi08nHG1aY1dBUa5M6ddeSNjnldPIH7b9HpPHtCjOjnql+W39OdEA/Ub1er7e9zqn1+8aZURs1sSMB51F4rGX+8FjGTiKa0DH2ziAoSe8b2yo7adx+3858V1EZdvxBP1VZd2zo2xcIvPLriu2ZJr98KuUksN11El98QrM1TX+mDnL5Vinvgb/pFJoIvHbXS15R4FWjTSrVXXvb5JB2qFS/O/ff09Rv2VT2l6jfNp8T7W6v9f5/SL3+JL3e9jqnNu8bl9AxxhjhYJ1OR1Qd0LyyYy0KxnoaeptpgC1L9su7ZoPdQ9mCcTzD1A/bl5kNJEVy+z1N75P/F2z7812OwsWDPvvr52MkWU6oRckTzqcv69Y3yB1/6mFWPLMV/VV7/cd//5ck6f/+538vXJLfjXY4Dn0MyrBvZBF41cSOBJxH+4+1OGD7eqmxRsuZtL8Ofy9O+NuBdjgOfQzKsG9k/XXpAgDA9YoUjJ/0ce9r0dKgCwAAtAOBFwDUEsntP+nr5V2LPUMGAQAACLwAoJauJovFpQsBAACuBIEXAAD41Xi2C8A5EHgBAIBfKZlUI40gDEBT/t+lCwAAAAAAt+6vTqdz6TJcLeoOOA+OteNRh+30r3//p6TiOy9oVtmdLY6Veqg3lPnnn38uXYTW+Iu59ethXQLgPDjWjkcdthcBV/twrByOPgZlOp2O/v7770sXozV4xgsAgAv5v//5X05aAeCX6Bh6+1r4QwmcB8fa8ajDdqN9Lo82OA71hzLsG1lMrgEAAAAADSPwAgAAAICGEXgBAAAAQMMIvAAAAACgYQReAAAAANAwAi8AAAAAaBiB17UIxup0OhoHly4IgFigcaejztZrLA5TAACQ147Aax1UXO8JTCS3nyt731VU9tmh0VMwVmfoNVBuAHVF7quKjkrLedbg7KW5lHz/1pcb1dmmSDqwLfpbUCffJssLoJ329SWxyO0feIH7wD7q57xwF/qoW9eKwCuYlwQV9uhKTmC6miyMjG9LkmzfyCwm6m59ZskJjczswF81mMmEjqwTlxpAXZE+PxQfzyb7Wky6ly7cmURy+0/Se/LbQznWUtNe+iSgyjZFWbvqd4aSv07nS8PMiU2dfBssL4B22tuXSEkg05suT5hvvi/xZS+n6u2M6uijfgVzaaFjHL/obcvYBe+3RWHV+baRLOOERR+p9LNKQsdYUqvrBGhCG7qpLb5tJMUvyzKW7Zuw7rF9Bo3UYVHfve6nrKSjq7JNAd+WUa6zy7xXJ98Gy3usVu7jvwxtcJy21t/eviTtgPOs/fmG238TfNvIckxpT9LiPuoYbd03LuXyd7y6E022bgAFepvea3Qdt7v2CsYdzWVvvZceepjc4s7ejk7dxn76kCStXvult7UzeXQ66mcuf8R59d0otV3qCklquGc/d9kkne/PxZrc8NDk/czvyg2vzP/mTB59V0Gm/Ovfl2yT1EnJ9wLnlLlLv1xq6Q3V620fOzetqO/u/tG9pPs/3erbbAk09yQ79wdgMLIlbx73C3Xybay8ANqpQl/SWL5ddXNdRjD3ZL8ko6EK0Ef9CpcPvIoEc61u5DmJYNzRfGQ0G2XfH8yMfFuS7cvMBupOFgodS7IchethisF4KM9yFBoj83KvpSQ9vssYI9/2NExFHZHbV+/jMd7WxEMbl9Pe+nmyQOPOMH4e5eNJT3pP3Z5eBziD2c9QyeXHZ2occqTPL8lSPIQyHiUZaDz04iGVJv4d3qurSJG+tS5v6MhKhlYaI//uW73cb9ZglvnNg6QOZMs3Mw0Uyf0exb9nMVG39HuBM4pcvZaMjl5Oe78r+MqLvrWyHD3v6rz3bRN9a1WaeKXvsuqt8t110tTJF8Dl1e1LGsj351zw0H6EPurmtDLwCuYrPT5cf+Qeuf16B5qknysqydWR3p0sba5oxFdWXuM7VpGrp+kyeyUlCWq8V7nRQDMTyrGk5f3L+hmUribvjix5mqcu+1i2LWs51VvyXvSpr7tH3Wd+2LdWsnTXi//bu7Ok5ZdCdTWZFV/NGUyK3g/0tmNMdeQ+6etPqvJKvxc4o+5Ei+QCRxjKd+zM85fL6duVTAp0esHbhx7fd1zRrbiNUsf5Kb+7Tpo6+QJoi8P7klPmm4wYGnqSNzx8cjX6qNvTwsAr0Hz1qGuPuyK3rye97w+6vOHPsLnMg525IGNL706WlvoKJYVfWhZs2/1zLyXbrFnpjda3p1fpyzN3z3qxJW8djUWfX7p7+JPLeKKFWWjSja/iHPRA6uYHyu3PdecUTRniadjpbNffSb4XOKFuV4PJTAsTyv8ZTXzEldRrFow1H8XH51HbNPXdddI0VV4Av0J3sthMriFtLphXQR91k1oXeEXuq1aPD9cduX+O9aT3arOb2f7PbGhhYRBSVTbAkvRzl+xQm3HKgd4+7gqD4OR5rfmoTrm/17PyzPRQ+Lkt3/i6Lxi2ddz3Ak3pajCL7yr/SpGr/ny0+0JTlW2k9QWh7f4s+l5JutfWYwxV822qvADa6dC+pNF8B5qFzuaC+T70UTerZYFXPEXzdQ8zXGr6NTp+SumSA/tH+i7XOsDy5kHBNnb5JCXru2pb9T0YyZan135JEByMNfRs+abmMErvQ3rfd4VmoGfHyg7bOvZ7gUZ19fBo6ag/6NcochVfR0kdlIGbvapbZZsfA43s7f4s/FpuLzFyUL5NlRdAOx3Ql5wj3+4f3VcZokgfddPaFXhFn/rQtQ8ztOSc5AnH4gM7EcQPgMXBS3eiF1uSN0zN8hfJffW2FnNNBzLB21RLq6i+4+9eLu/1UhAdxVd1NsOpwq+CIX/hl0oHAibl3qM7eZGtzSQilb4XaNx6ttH+WEHBH7lftYBy5Krfm2q5nKqXnsX0VZt+pco2OYNnR1Z6SE5y0SV9klEj36bKC6CdKvUlZ8o3GA+1ct53n//QR92+S81jX8S3r2edqmzVhcaxtFnXR0qt1VDwme2v1/Xa/D90rGppf1622V7Kwcpsk63LOC/Lto219T0msy6R7Zt4XQjbN8b4xt7KM/eenaRdr1O2XlMi/fvir9i8Zznh1m/2M+Vf/76fctnG3/e9uEkt66Zy+7dlbH+zvopt71ij5YIaqcP0Wma51896MlW2+Tmuc31app5zn9XJ92TlPb3W7eO/EG1wnFbX366+ZC1zTpY/PzpRH7V9fns9fdQxWr1vXEDHGGP2BWfY1ul0dNaqW1/huPfrDrOL5PZ7+ngMjx8GCZzR2Y+1CqJgrKeht7mra1myX941G7Tz2GpjHWKD9rk82uA41B/KsG9k/XXpAgDAtekOZlqY2aWLAQAArki7nvECAAAAgBvEUMOaznrrNBirM/Q2/7d9mYPGGwYad4b6yeHg9MDlMEzheNRhu9E+l0cbHIf6Qxn2jSwCr5rYkYDz4Fg7HnXYbrTP5dEGx6H+UIZ9I4uhhgAAAADQMAIvAAAAAGgYgRcAAAAANKyjeOE1AAAAADip1Wp16SK0BpNr1MTDgsB5cKwdjzpsN9rn8miD41B/KMO+kcVQQwAAAABoGIEXAAAAADSMwAsAAAAAGkbgBQAAAAANI/ACAAAAgIYReAEAAABAwwi8AAAAAKBhBF4AAAAA0DACLwDYEmjc6aiz9RorKNw+ktsv2r6jTt9VdObSAwCA9iHwAoCcyH2VV/C+5TxrUJiiq8nCyISOrM3WckIjs5io21A5Ly8XcO4IMiO3r06no3Fx5FogHfyWBbyH5psPkPtytwpcZZs2q1b+pN6SV7/Sj9zXJnXq7je0CS5tfz9Rrb85LE31/rE0DcfDzSHwAoCMSJ8fioMmk30tJrcbQh0uktt/kt6T+vFlL6fqbZ3ZxCcJvenygKxd9TtDyV/n7UvDrRObQ/PNlzeUYy017aVPWqps02bVyh+5ffWm6X081ONHb3fwtbdN6tTdb2gTXFaFfqJSf3Nomqr9Y76sHA83z6AWqg44j7Mfa75tJMUvyzKW7ZswrJg2dIyVpJVlnKrpGtZMHYbb9eLbRpZjCn/2um5sf3/Ovi2j3IZF7x2Ub+gYJ7/NOq2VNFSVbRpwsvapWH7f1lY7hY5VXL/pNLvapE7dtahN+Jt+nNbX345+4qD+pnKaA/vHdRnbcjycUuv3jTPjjhcApATz1CDD5VJLb6her+pQrN+kq27uBmAw92S/HDu0MtDck+xRdlDnYGRL3rziEKAC3Ykm+XGi3T+6l3T/p1t9mzarWP7ByJaWUz397NOB3qb38mfFA2krtUmduvsNbYKWq9PfVElTo3/kePgVCLwAIBG5ei16uEvScrpnKNYvF4w7mo+MSs/dq4q+tSr9cKXvUzZB9K2V5eh5V5mrbNNmReUfzBQ6lpbT3voZkblGZlby/KLqt0mduvsNbYL2qLNv10hTu3/keLg5BF4AkOhOtEie6QpD+Y6dmixDWk7f6t9xuVHJQ+tDT/KGHXWqz56xg6W73gmy2SN4+9Dj++47dFW2abOy8ncn73J+du4qAe3hbVKn7n5Dm6Bt6vQ31dIc2z9yPNweAi8AKNLtajCZaWFC+Xby5onvuNyA7mSxeXhckrzX63jIOxhrPlpo53wpVbZps9LyBxp3kgf0k4fzD5lx8pjvPjLNtbcJfpWj+keOh5tE4AUAO3U1mIWpuwPHi1z3Bu+cDTQLHVla6is8IpvuH90X5BF9ryTd6ySPMUSu+vPR7mE/VbZpsx3lD8ZDefbL+mQtXgrBtyXvtWS660PbpE7d/YY2QfvU6W9q9VEH9o8cDzeLwAsA9urq4dHSaU78A719SGcYSXd+3T+6P3qY4EDxM+rZ0DT8Wkr2qPw5pKoiV/0n6T19thK42avQVbZps53lj/Rd8IDKYGRvv7n5tHqb1Km739AmaKk6/U3NPqpq/8jxcNsuPKvi1aLqgPM477HmG1sysmzj52bmDR1r/3S9VaaT3zelcAPOVYe+vXvq8KrTycfbpurPt41km8KkB+erzXIBP8sGpNqjyjYndtL2qVD+0LGMMnUWGsfaMx11lTapU3ctaRP+ph+n9fW3q584pL85Is3O/jFXzksfD6fU+n3jzKiNmtiRgPM467GWC5xsf7N2im1X+KO2lT73sW/Hn1eKEk6nkTpMr3e2fpX9LN/edYKwDnZ3nsQXn9AclG9BeZPXz8lQlW0acLL2OaD8SfBV/HmNNqn03e1tE/6mH6fN9be7n1jb2d+c5njY7h/bezycUpv3jUvoGGOMcLBOpyOqDmjeuY+1KBjraehpmbxhWbJf3jUb7BpjGMnt9zRd7tgkzfZlzjgwn/6q3Wify6MNjkP9oQz7RhaBV03sSMB5cKwdjzpsN9rn8miD41B/KMO+kcXkGgAAAADQsNYEXskic8mrf1VTs0Ry+51M+bdeJ10gBQAAAMA1aUXgFbl99aaSE5r1QnOhHj96VxR8xeugGN+WZKV+R/LyZa++i9dHAQAAAHDzWhF4hV9LyXrUw8+z6/GaOcujVuFsk4Fmi4lYWBwAAAD4nVoReA1GtrSc6unnDlegt+m9/JtYjjuQW3DnLju0sv+z6F0w3j9UMZt2rPwgxlp5B+PCz/IjJHcOCY1cjd0gM+wySZ/57nGQzafvxncDc2WomtYd7/gtSd4V6g0AAABozDnnrt8lu6bInoXrWqCw6nzbbC2a6ttbayv4dnodiXjhyvg3h8ZJ1grKLc7nO/H72QX41mlTa1Ick3fcBpu6L/x/ev2LZD2JZHGKXL759L6dXb8om1+8nkXycfZ37Etb7fNd9Yb2alE3dbWow3ajfS6PNjgO9Ycy7BtZf10q4MvrTt7lfCTr4Kz0HUk7l81praWmvY6mqXcs53nzn8jVq2fJCZOhh11NXmxNh+t/zyaFuQ4mEyly9eTZejFJxSRpp3oLJpr1jshb2noGLRkC2luX+2m6lO0vNkMmBzOFzkq96avc54Em3YkWZlKcfp/oWytZelxv3LuzJO9LoVRjiGagt2n83VqX/XVXvd3CjdUb1+l0Ll2Eq0cdthvtc3m0wXGoP5T5559/Ll2E1mhJ4BVo3HnVXWhkuuuFSHsdffnmCk+KLTnhQpPkHD8Yq/+d+jj80lL3eklHE4OZKi1xEH5pKU/Djrf10eo7knRE3j82+VtOKDPrpr57Exglun/uJXn6SkdIwVidoSfbNzKzfPZDZYqfBEepoC0YdzT0JOm+WtqMSG5/rjvHkj6UKvuOervOCP9XMawBchTWUWk32ufyaIPjUH8o0+l09Pfff1+6GK3Rime8gvFQnv2yDlbiGQJ9W/Je3eufCXAw0nZ4EN/Rq8VyFJr8rIlGi59I74i8JUm2/HWeL1+9zDNi0lJb85307mTlsxjMZIzRaF7wLJXt/5Q5dLIpk2e55qPtz/aljX3L7T9J7zM95D/aW28AAABAc1oQeEX6Xm2/OxjZ5y9KIwaaTLrriSeidaBSEMBErtx9sz307mQtP/RZFlgdk3dRyZ8dWVrq4zP6CbC8eS6j8EtL2RoV3JmM03vKJykUjDX04qCv9l1O70N6T91tTOyrNwAAAKBhLQi84qnj5Q1TM+hFcl89WY8PNzIFe6Bx70N3D12pO9GLLXnD9J0kKXj70p90wBF+aZnPpjvRi73UtJe9ixS5/bjujsm7QPT5oaWk+z+bche2k/OsQbocmfSW7io85BV9r5S+Wxd+VSlhzs9d05x99QYAAAA07cyTeZTKzmqorZkA2yZbdcnsgTteuRn0fDv7uZ2exjF0jJVOa2fneMynLZw18dC8kxkKtTvvfDvlilb63Zn3bT+bj+WYcD2r4U86OymPZSxrd1rHzpZ3O+9q9YZ2alE3dbWow3ajfS6PNjgO9Ycy7BtZHWN4GrIOHiQFzoNj7XjUYbvRPpdHGxyH+kMZ9o2sFgw1BAAAAIDbRuAFAAAAAA0j8AIAAACAhhF4AbhigcadeP237Cu3flw6xbhg+37ZmoGR3P4h25+yrEXfnZ2xtPD3MFUnAACtROAF4GpF7qu8gveTJQ6KDGZGxviy02twl63zFn3qQ1ZqkXBLtm9kFpODl7o4vKzxYvIm9LVZ1XB7WYTBbL2NZcsPjUzthfDqSgeU5QHvz9bjqsHhvnzzgel2ULqtSpo6+bZNE3VXI99KFyh+S5vgcvb3UZHb53jAWRB4AbhSkT4/JCc0Mib7WhQu6JbW0929nQq+1guF57/h80N6fNR96r0q69KdtKzdnu7SQaI8DfN/wLs93d3fqXfuhQ8jV/3OUPLXv8eXhjuCr8jta1gUfR6cbyS3/yS9J/UYyrGWmvZ2nYBUSVMn35ZppO7q5OvLXk7V2xlk/5I2weVU6KMit6/ex6PCpF/27zke0Jym56u/VVQdcB6lx1p67TnLMpbtm7Dy0myhcWzH+CVrvq2/wNiyjBOm15izTK3l305Q1jC/1l52gb54m5IcmuqvfLtkncH8An/GxGsIWraxrZLPD8k3dIyTz2K9RmHp+nxV0tTJ9wRO2T6N1F2VfE24vU/7dsFxlf3etrQJf9OP09b627/fxv174ZqkO/bdWz8eTqmt+8alUBs1sSMB51F2rOUXxE5e1f74JIFKbuHu9B80317/ET0+8DpNWXctNH+JwKv4hCUOMm3jb21rGz9ZbH5n4HVIvhXS1fkNR+d7mNO1T1N1Vy9f365Tb5dpE/6mH6ed9Vdhvw0dYxX16769o7+//ePhlNq5b1wOQw0BXJ/I1WvJkLXltKd+5TEXA402D1DJm2+GgQRzT/boBM9LnaysUneykJ8q73La08Xm0oi+tSr9cKXv1M8Kxq+6C2elz93VzXcrneXo+ZAmq5KmTr6X0lTd1cg3GHc0Hxkd/MjhrbUJLqfyfls81Pz4fDc4HpAg8AJwfboTLZLx+GEo37GVmStj+rZ3kofE4NnZpPXm63SB5p6tU8RdpyyrJA1moZxUBt7wkmP7rb3PvEVuX/PRQnsfuzsw37zg7UOP74dNelIlTZ18L6upuquWbzJJwdCTvOHhs2zeZpvgcvbst90HPVrScvqU6UeDuSfpXn9KdzKOB9RD4AXgunW7GkxmWpgwdTdox9X9rfTxH96Yp3kgKZhrtWNmxIuVNc5Ek0VupsOnN32dsJgnE7l60/vhV3kPFYwPD+6qpKmT77U58W/sThabyQQkyXutfmGANsHZdTVZJBNUbGYKHHqSrDvVmkspnTvHA3IIvADciO7W3aCq6R42kZe817HGrys9PjT5l6xuWRMDzcLUnbqlJ6987Eszun90r6W+wuzb0fdKyZXi4G0qb9pLTXvc03QpyRuq0+kUD5OskG/2A1f9+eiw4K5Kmjr5XlpTdXdovpI2++h2ukK32ia4nMr77Xrpjp+RCXHfar+U3EXieMARCLwA3JAkiNo1RKQg1eRlcwdp6cnToxqNu+JvrVXWTfKJFukHvs4ufj4u/VycJIVfS8keaaBkzbT0ax1s2r6MKXveYX++PyJX/SfpPZ1R4O6fBnpfmjr5tkJTdXdAvmndP7qvMiTrptsEl1Nnvw007k0lJ9wR0HA84AiXmtXj2lF1wHkUH2vrmQYt2/i5WadCx6owW+D2LIDpmQezs0OVzWoYGseOZxm0dswo2ERZ83mocDr8jcb6q/yMYHtnz6syq2HFfNdTKCv/2jNd8940dfI90knbp9G6O6St42Nq7/7dkjbhb/pxWlt/B+y3SV9aabbZGz8eTqm1+8aFUBs1sSMB51F4rGX+8FjGTiKa0DH2ziAoSe8b2yo7Gd1+3858V1EZdkzle6qy7thw35ozjfZXmd+3+8SjOPBKAttdwUHus/yaZoVT7OfyrZKmUr6nd/L2OXXd1cx3+5hob5vwN/04ra6/nX1U6sJaaR/6+46HU2r1vnEBHWOMEQ7W6XRE1QHNKzvWomCsp6GnZfKGZcl+eddssHvcXjBePzidsH2Z2UBSJLff0/Q++X/Btj/f5ShcPOizv35mSZLlhFqUPOF8+rJufYPc8aceZsXPJNBftRvtc3m0wXGoP5Rh38gi8KqJHQk4j/Yfa3HA9vVSY42WM2l/Hf5utM/l0QbHof5Qhn0j669LFwAArlekYPykj3tfi5YGXQAAoB0IvACglkhu/0lfL+9a7BkyCAAAwFDDmrh1CpwHx9rxqMN2o30ujzY4DvWHMuwbWazjBQAAAAANI/ACAAAAgIYReAEAAABAwzqKF14DAAAAgJNarVaXLkJrMLlGTTwsCJwHx9rxqMN2o30ujzY4DvWHMuwbWQw1BAAAAICGEXgBAAAAQMMIvAAAAACgYQReAAAAANAwAi8AAAAAaBiBFwAAAAA0jMALAAAAABpG4AUAAAAADSPwAoBaAo07HXW2XmMFly4aAABondYEXpHbT5249OVGly7RISK5/dzJV99VVPbZ+NZOy3b/xk3bXlu7AuUi91VewfuW86zB2UtzWckxXt61pYPUqoHpvjT5fqdK/1IlTZ18AbTXgX3Jz/nbJfKlj7p1rQi8Irev3sejQmNkjJHx7zXtXdOO1NVkYWR8W5Jk+0ZmMVF36zNLTmhkZrd2WrbjN0au3vQuEzqytNRXeNGCAicS6fND8b5usq/FpHvpwp1RfALQmy53bOKq3xlKftK/S8N9wdfeNJHc/pP0ntR7KMda7vm7USVNnXwBtNbBfYkvezlVb98F8kbypY/6FczF+caWjO3n3rVlZDkmvEyh9iqsOt82kmWcgkL7tko/uxkFv9+3b/w3o3Gt6KbyfNtIil+WZSzbN2GL9/PG6zB0jFXQjxuz7vtyHxS9d1Ca0DFOPvm6DFZZh1MlTZ18T6CV+/gvQxscp631t7//CYWe4kQAABBcSURBVLf7bt/ee/7ZSL4t7qOO0dZ941Iuf8cr+tZKlu562bcHI1tafujzBiL4YNzRXHbhZ2VDLINx0bMjZUP44lc/c7kjvgXed6PCoX6Z/MeBFIwLbocXP8PSr3xZJdBcLyq8AZD+vvQQpcjV2A0yt9EzF4gK0+Vuu2d+T/bKeu36Lilvvh4z+Sf1WPZbcbWCeWqQ4XKppTdUr3fIsfFbBJp7kj3K3uUfjGzJm5fc9aqQpjvRJD9woPtH95Lu/5TccaySpk6+AFqqSv/TVTd3aAdzT/ZLMmrpjPnSR/0Klw+8JElLfdxChFUgGHc0HxnNRsWfbYZYJreLxwoU6VtO/H7oyEqG7xkj/+5bkYqGZ9paTnvrQCHQuDOMnz/5eNKT3nP5S4OZkW9Lsv14WOBgptCxJMtRuJioq0hufyhPtvzkNrkkywkrDqUKNO7MNSocVhloPPTiIZkmLof3uhn7vJq+/txGDx1L3jAJnsrSxUMd45GelpzngTR4lmPZ8s3s53mb+vVdXt58PXYni1w97v6tuEKRq9eih7skLac9gq+06Fur0g9X+i6qqjppknSWo+dDRnJXSVMnXwCXV6Mv+Tln29cnNJFv2XfRR92Uywde3Qc9WtJy+pQZnxpfUb7XNQfwkdsvP9AiV6+eJec99SzYS3JXrKvJrPiqyGAyUTdy9TRdZq+cJIGT9yo3GmhmQjmWtLx/WQdKXU3eHVnyNC+8zBzoreg5DXt04EQBS017HXU6Q63KJhnI3eXs3VnS8kuhJHUnWpjFz12y8GspWXfq7UsnaTBbB1NPrtzxk/S+CbqOq+/d37vTMWnRTt2JFskFjzCU79iyUh8vp2/MapixPaKhiTTB24ce33ddpa6Xpk6+ANqiWl+SjFYZepI3rDIJWlP5ZtFH3Z7LB17qarJI7j5shmMNPW1OuK9Q5Pb1pPfyqxvhl5b5wHIwk0ndoSkVfmlZcNB3/9xLuQksrPRG69vRq63LMZHc/lx3Tvr0sauHR0vyhgcOjVvfLVrfgSu8+p8KroJxyYP56+F581FqopK96bqaLOIHWD/u3rNDHI+p7yrl9YY/+27m8yppcb26XQ0mMy1MuL7jKu28K4NmBGPNR4viYc3HpKmTL4Cr050sNpNgSOuL2BfOlz7qJrUg8JJ+ZsX7uYrsyJL2jLFtsc+xnvReYUjeMSdoBTME9u4yV96r+V7PkDPTQ+6T7mQhEzpaDeM7WCWjq4qt78Dl72Qmkmej5qN4OGFRemOMRvPsc1p700XfkmVpOe0VBIz163vv99r+z/6b/3xvWtyA7vqO66XL0TLdP7ov6Kui75VKRzQcmiZy1Z+PDhvCUyVNnXwBtEed/kcDzfbNwtxUvpnM6KNuVUsCr7RA495UcsIr3ZmWmn6N9gddvbviAzBy5e67w7QOsLz8mMHwS0vZGpXV23rY2+NDqmzeh/RefrUkeJtqKVt+crXmAN3Je+a5sk2mYw29+NmxfW08eE4Nj9ybLtD4SXpeLOJnqYap7z2mvg8o70nT4sqs7xJf+RDp0xooft48e5CFX8sdw5gPSBO5iq8bpd4N3N1XlKukqZMvgJap0/9oHVjtGkrYVL5r9FG37fwTKZYLHcuoxVNiphVW3Y7p5IunWt+eYt63bePvSbdJm56+OTSOla67+P/SJr/8FP356VBDx8p8HrdH8t3xtP8726awrHG6re9JbRf/lricoWNlpqROb7srXfx703W3/v3531ujvnd/7+563JcW+7WsmzI/+7RlGz93OISO1cr+q/E63DGdfPxZ6pjy7f3HQJU06+9U/rVnuua9aerke6T27eO/D21wnNbWX43+x7crnIc2mm/7+qhjtHbfuJAW1Mb6JKbFO02R7I6UBDlFB0DBZ6mzkySASl6ZE5f8wZU7q0kC1cK0SSBm25s8toIQ/QS6mbws29hWOs9UGxUGX7t/Y2bNI9vfys+2k8/jTqy8TsrTWVb2e7O/p/h3V6/vCt+73n77e3f/VuzXuk47s59Yxk6ir9Axtt3OPqzJOswfU4X9eKbO8icnyTGyK7AqukBScOKR6Z9y+VZJUynf02vdPv4L0QbHaXX9HdiXbF9AOk0ftTffFvdRx2j1vnEBHWOMEQ7W6XTU7qqL5PZ7+nisOv070E5tPNaiYKynoaefqVIsS/bLu2aDdh5rbaxDbNA+l0cbHIf6Qxn2jay/Ll0AALg23cFMCzO7dDEAAMAVaeHkGgAAAABwW7jjdZMCjZPp35c9db58GabUAwAAAC6GZ7xqYswqcB4ca8ejDtuN9rk82uA41B/KsG9kMdQQAAAAABpG4AUAAAAADSPwAgAAAICGdRQvvAYAAAAAJ7VarS5dhNZgco2aeFgQOA+OteNRh+1G+1webXAc6g9l2DeyGGoIAAAAAA0j8AIAAACAhhF4AQAAAEDDCLwAAAAAoGEEXgAAAADQMAIvAAAAAGgYgRcAAAAANIzACwAAAAAaRuAFALUEGnc66my9xgouXTQAANA6Fwu8IrevTqejcekZSvqkpu0nMpHcftEJ2PrVdxVduogATipyX+UVvG85zxqcvTSXtL+vTvr7+NWXW6lD3Jdvvt+tkm+VNHXyBQBgvwsEXvEftd50uWMTV/3OUPKNjDEyvjRsdfDV1WRhZHxbkiUnXJfbGJnQkbWcqtfq8gM4TKTPD2WP9fVrMeleunDnU6Gvjty+eh+PCpM68u817e0JZvbmG8ntP0nvSb2HcqzlnnyrpKmTLwAAFZlLCR1jScb2tz/ybRnlPih675IKq863jWQZJ8y+HTqWUclvBbDbJbupUr5tJMUvyzKW7Zsw3J/sUpqqw/19tW/sgr7Pt2VkOaasyvbmGzrGyfen678pVr4DTn2+N02dfE+glfv4L0MbHIf6Qxn2jawWPuMVaO5J9ig7WGcwsiVvfpV3jbp/7gvf3zf8Jvt56mpvMP55v59LlE4zDqRgnBoyE7+RGwIZD+fpu1Eq7aYs+fSZMiVDKNN5bg0fLX4OJl/uou/aLuvuesuk7+TyKkybL8dhdVFcvuq/F9crmKcGGS6XWnpD9Xq/rZ0r9NXRt1aydNfT9jbLD30WVleFfLsTTfLjObt/dC/p/k/JHccqaerkCwBAVRcL+crueJW9X3I36VIKq66wjPEVX8k2fmbT9BXf0DhWdhvfTl9hXX+evkKcXHHPXDUOjWNbW/WXv3ocOtY6XVI2Gcuy1t9XXJbi9Jvfl3y8+3fF2+66crz7u3blHxrHXr8fOsZKtYPvxO/n8/qpQ9tPtdMxdXH478V+l+ymCq37KJW82tjejdRhlb667G7Rrv687t+A0DHWjrtotdPUyfdArdvHfyHa4DjUH8qwb2S18I6XpIIrpNdjqWkvfbdjKM/2Zcxs88B95OrVs+S8TxRfQ+1q8mJvsohcvXq2Xn6eFVl/vpzqLXU3ybJtWen3ok993T2q+P5aItDbz/N1A81MKMeSlvcv62dTupq8O7LkaV7l9mLuinbvzpKWXwrT29ijmpMNpMuqPfXW1WSWvJ81mEzUjVw9TZeyX1LbDGYKHUvyXuVGdeoiV76jfy+uQneixc8znKF8x5aV+ng5fbvKO/P17Omruw96tKTl9ClzRz++Y3iv8ptIh/8NCN4+9Phe3Acck6ZOvgAAFGlp4HXNcpNrmFDOapgdghd+aZk/6RjMNsFZ+KWlPA3Tw9WG8dCm1Xfq7OXuWS+25K2jgujzS3cPf3aULZLbn+vOsbY+sdJnOeuhNZnv8oY/ZclMjNKdaGEWmnTjoXjZSVO6eni0JG+4Y/bKA8q6r952Cb+0LDiZi4eBLvWVihT31kVZ+Y76vbhK3a4Gk5kWJpT/c+1kpa3d5dfqarJIJqjY9GdDT5J1p5NdXwvGmo/ifuikaerkCwBAifYFXt0/us+dCEtS9L3S7iukbdXVZOHLluQN07Ny7Tk5s5zNLGA7ZkzbPPcQ6O3jTg+l9fO9nq1rpoc6P8P2f8oQ5gK35Nmn+Wj7s+5kIRM6Wg3Xd/8qfdmush5zUru9X6l3p+0wdJ/y8tX7vbh+XQ1m8R3TX6NyX72e9TU906uUvftcK9/kA1f9+UizQ24zV0lTJ18AAHZoX+ClgUapuziJ8Gt5O0O4eneyioKAyJUbrD8vffA8ZzCSLU+v/VetHh/Kh8N4H9J7xSu36+GDj+VR3EYw1tCz5RtTeoISvE21lC3fxAHoXmVl3Vdvu6wDrPx+Fd8JszUq27GK6mJPXR78e3Ej1nc8r/ICUR11+upA495UcsIdAc0B+Uau4msgqXcDd/9U9fvS1MkXAIA9Whh4SYNnR5b3uvkjl5zcX+Wlx0huf33nIzlp6E7iIYLD7EyGwduX/gySz5ea9rbXw9kewhafpCyX96lnwgrYLzuDrvRzKcHbVEvrccfds1SZvldK34UKv7LPPEVuX0PPkhNWGA64r6z76i0Rfmnryat12uwwwEjuq7e14O3euthRl7V+L67MeubK/lhBwYn4b1pA+ZC+Op4pdKiVE+5d66xSvpGrfm+q5XKqXnpY9qvK+64qaerkCwBAFZeY0cO3czOBFc0YlZk5LDsjYBtkqy6Zze6wmc7y9VC41k1RHqk1hGzfxHWVm5kv+Sydh+WEP2uKbeo9Lrtl25v6zs8imLxv+wXpc99p21u/Pf5d2e321UdxWSvUW37GuVylZvLcqvPqdbFdPtvY1mG/F9VcqJsql9nHLGP7mzWgbLvZ2e/qarQOd/bVqeOgdGbA4plfd+brb/cz28daLt8qaSrle3qt28d/IdrgONQfyrBvZHWMMeaAOA1rnU5Ht1F1kdx+Tx+P+69C3z7qoo3aeKxFwVhPQ29zZ9WyZL+8azZo537TxjrEBu1zebTBcag/lGHfyPrr0gUAgGvTHcy0MLNLFwMAAFyRVj7jBQAAAAC3hKGGNd3GrdNA4/SU57Yvc5UTmJwCddFWt3GsXRZ12G60z+XRBseh/lCGfSOLwKsmdiTgPDjWjkcdthvtc3m0wXGoP5Rh38hiqCEAAAAANIzACwAAAAAaRuAFAAAAAA3rKF4cEgAAAABOarVaXboIrfEXD7zV888//+jvv/++dDGAm8exdjzqsN1on8ujDY5D/aEM+0YWQw0BAAAAoGEEXgAAAADQMAIvAAAAAGgYgRcAAAAANIzACwAAAAAaRuAFAAAAAA0j8AIAAACAhhF4AQAAAEDDCLwAAAAAoGEEXgAAAADQMAIvAAAAAGgYgRcAAAAANIzACwAAAAAaRuAFAAAAAA0j8AIAAACAhhF4AQAAAEDDCLwAAAAAoGEEXgAAAADQMAIvAAAAAGgYgRcAAAAANIzACwAAAAAaRuAFAAAAAA3rrFYrc+lCAAAAAMAt6xhjCLxq+Oeff/T3339fuhjAzeNYOx512G60z+XRBseh/lCGfSOLoYYAAAAA0DACLwAAAABoGIEXAAAAADSMwAsAAAAAGkbgBQAAAAANI/ACAAAAgIYReAEAAABAwwi8AAAAAKBhBF4AAAAA0DACLwAAAABoGIEXAAAAADSMwAsAAAAAGkbgBQAAAAANI/ACAAAAgIYReAEAAABAw/4/QSVsf+Y6nKAAAAAASUVORK5CYII=[/img]