Сравнение двух таблиц
Имеем две таблицы (например, старая и новая версия прайс-листа), которые надо сравнить и оперативно найти отличия:
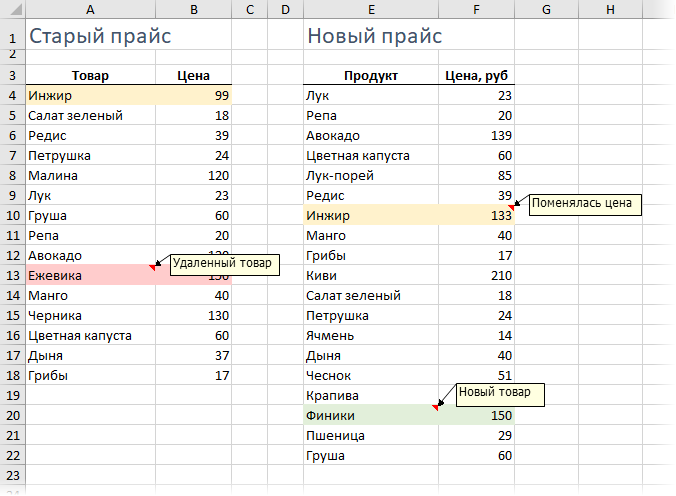
С ходу видно, что в новом прайсе что-то добавилось (финики, чеснок...), что-то пропало (ежевика, малина...), у каких-то товаров изменилась цена (инжир, дыня...). Нужно быстро найти и вывести все эти изменения.
Для любой задачи в Excel почти всегда есть больше одного решения (обычно 4-5). Для нашей проблемы можно использовать много разных подходов:
- функцию ВПР (VLOOKUP) - искать названия товаров из нового прайс-листа в старом и выводить старую цену рядом с новой, а потом ловить отличия
- объединить два списка в один и построить по нему потом сводную таблицу, где наглядно будут видны отличия
- использовать надстройку Power Query для Excel
Давайте разберем их все последовательно.
Способ 1. Сравнение таблиц функцией ВПР (VLOOKUP)
Если вы совсем не знакомы с этой замечательной функцией, то загляните сначала сюда и почитайте или посмотрите видеоурок по ней - сэкономите себе пару лет жизни.
Обычно эту функцию используют для подтягивания данных из одной таблицы в другую по совпадению какого-либо общего параметра. В данном случае, мы применим ее, чтобы подтянуть старые цены в новый прайс:
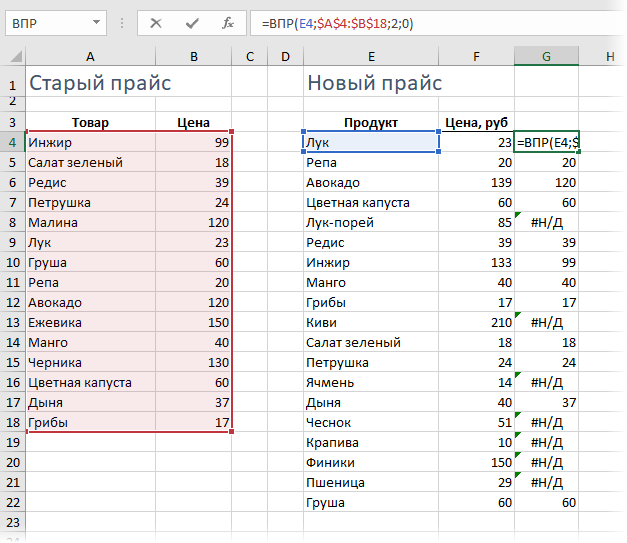
Те товары, напротив которых получилась ошибка #Н/Д - отсутствуют в старом списке, т.е. были добавлены. Изменения цены также хорошо видны.
Плюсы этого способа: просто и понятно, "классика жанра", что называется. Работает в любой версии Excel.
Минусы тоже есть. Для поиска добавленных в новый прайс товаров придется делать такую же процедуру в обратную сторону, т.е. подтягивать с помощью ВПР новые цены к старому прайсу. Если размеры таблиц завтра поменяются, то придется корректировать формулы. Ну, и на действительно больших таблицах (>100 тыс. строк) все это счастье будет прилично тормозить.
Способ 2. Сравнение таблиц с помощью сводной
Скопируем наши таблицы одна под другую, добавив столбец с названием прайс-листа, чтобы потом можно было понять из какого списка какая строка:
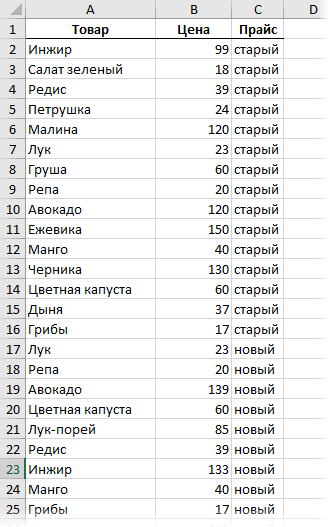
Теперь на основе созданной таблицы создадим сводную через Вставка - Сводная таблица (Insert - Pivot Table). Закинем поле Товар в область строк, поле Прайс в область столбцов и поле Цена в область значений:
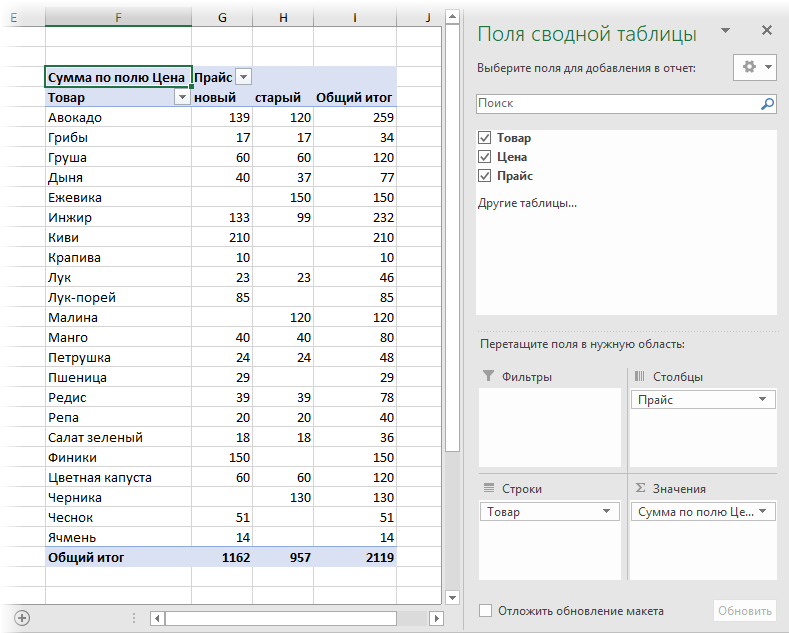
Как видите, сводная таблица автоматически сформирует общий список всех товаров из старого и нового прайс-листов (без повторений!) и отсортирует продукты по алфавиту. Хорошо видно добавленные товары (у них нет старой цены), удаленные товары (у них нет новой цены) и изменения цен, если были.
Общие итоги в такой таблице смысла не имеют, и их можно отключить на вкладке Конструктор - Общие итоги - Отключить для строк и столбцов (Design - Grand Totals).
Если изменятся цены (но не количество товаров!), то достаточно просто обновить созданную сводную, щелкнув по ней правой кнопкой мыши - Обновить (Referesh).
Плюсы: такой подход на порядок быстрее работает с большими таблицами, чем ВПР.
Минусы: надо вручную копировать данные друг под друга и добавлять столбец с названием прайс-листа. Если размеры таблиц изменяются, то придется делать все заново.
Способ 3. Сравнение таблиц с помощью Power Query
Power Query - это бесплатная надстройка для Microsoft Excel, позволяющая загружать в Excel данные практически из любых источников и трансформировать потом эти данные любым желаемым образом. В Excel 2016 эта надстройка уже встроена по умолчанию на вкладке Данные (Data), а для Excel 2010-2013 ее нужно отдельно скачать с сайта Microsoft и установить - получите новую вкладку Power Query.
Перед загрузкой наших прайс-листов в Power Query их необходимо преобразовать сначала в умные таблицы. Для этого выделим диапазон с данными и нажмем на клавиатуре сочетание Ctrl+T или выберем на ленте вкладку Главная - Форматировать как таблицу (Home - Format as Table). Имена созданных таблиц можно подкорректировать на вкладке Конструктор (я оставлю стандартные Таблица1 и Таблица2, которые получаются по-умолчанию).
Загрузите старый прайс в Power Query с помощью кнопки Из таблицы/диапазона (From Table/Range) с вкладки Данные (Data) или с вкладки Power Query (в зависимости от версии Excel). После загрузки вернемся обратно в Excel из Power Query командой Закрыть и загрузить - Закрыть и загрузить в... (Close & Load - Close & Load To...):
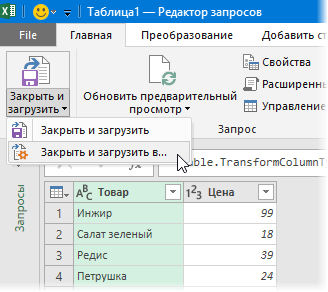
... и в появившемся затем окне выбрем Только создать подключение (Connection Only).
Повторите то же самое с новым прайс-листом.
Теперь создадим третий запрос, который будет объединять и сравнивать данных из предыдущих двух. Для этого выберем в Excel на вкладке Данные - Получить данные - Объединить запросы - Объединить (Data - Get Data - Merge Queries - Merge) или нажмем кнопку Объединить (Merge) на вкладке Power Query.
В окне объединения выберем в выпадающих списках наши таблицы, выделим в них столбцы с названиями товаров и в нижней части зададим способ объединения - Полное внешнее (Full Outer):
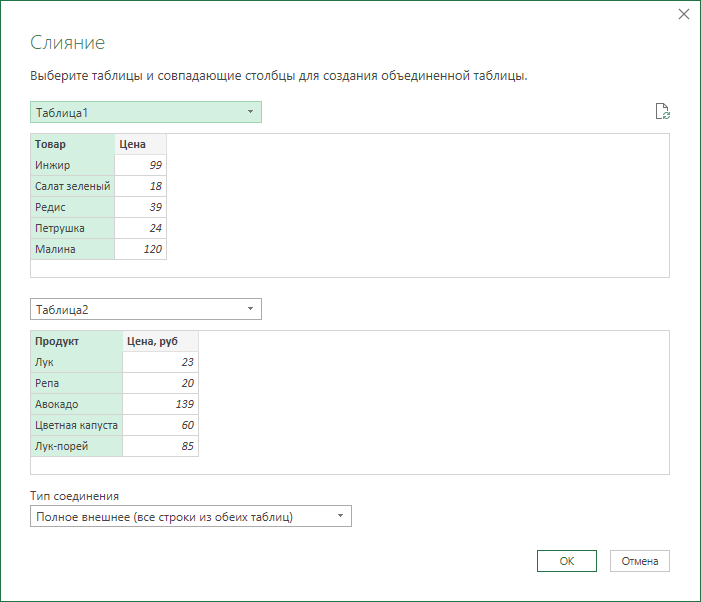
После нажатия на ОК должна появиться таблица из трех столбцов, где в третьем столбце нужно развернуть содержимое вложенных таблиц с помощью двойной стрелки в шапке:
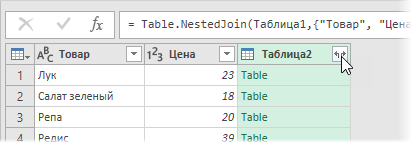
В итоге получим слияние данных из обеих таблиц:
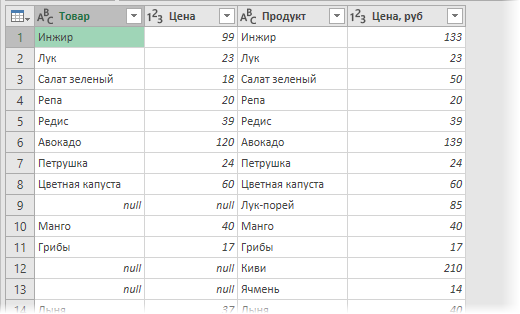
Названия столбцов в шапке лучше, конечно, переименовать двойным щелчком на более понятные:
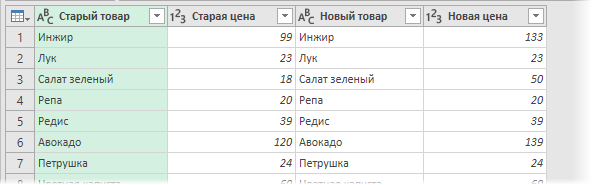
А теперь самое интересное. Идем на вкладку Добавить столбец (Add Column) и жмем на кнопку Условный столбец (Conditional Column). А затем в открывшемся окне вводим несколько условий проверки с соответствующими им значениями на выходе:
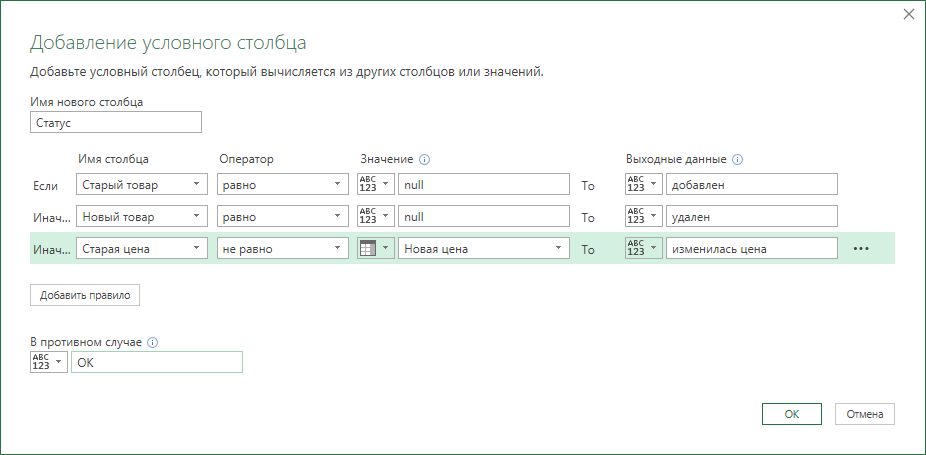
Останется нажать на ОК и выгрузить получившийся отчет в Excel с помощью все той же кнопки Закрыть и загрузить (Close & Load) на вкладке Главная (Home):
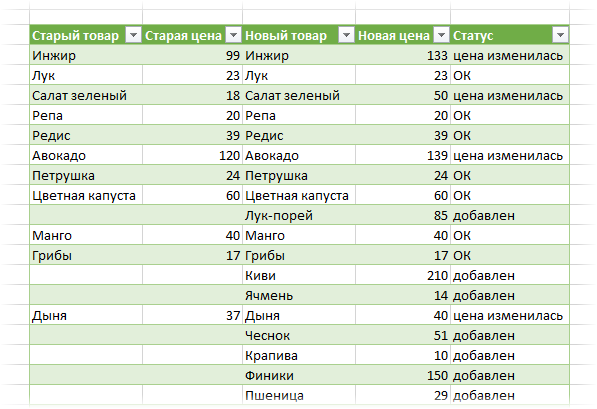
Красота.
Причем, если в будущем в прайс-листах произойдут любые изменения (добавятся или удалятся строки, изменятся цены и т.д.), то достаточно будет лишь обновить наши запросы сочетанием клавиш Ctrl+Alt+F5 или кнопкой Обновить все (Refresh All) на вкладке Данные (Data).
Плюсы: Пожалуй, самый красивый и удобный способ из всех. Шустро работает с большими таблицами. Не требует ручных правок при изменении размеров таблиц.
Минусы: Требует установленной надстройки Power Query (в Excel 2010-2013) или Excel 2016. Имена столбцов в исходных данных не должны меняться, иначе получим ошибку "Столбец такой-то не найден!" при попытке обновить запрос.
Ссылки по теме
- Как собрать данные из всех файлов Excel в заданной папке с помощью Power Query
- Как найти совпадения между двумя списками в Excel
- Слияние двух списков без дубликатов

Подскажите пожулуйста, если какой то инструмент или как сделать
1. нужно, что то типо расширенного фильтра, но работающего с несколькими исходными диапазонами желательно на разных листах (расширенный фильтр работает только с одним) или как его заставить работать с несколькими исходными диапазонами
2. как поместить результат расширенного фильтра не вертикально, а горизонтально
нужно для автоматизации сравнения двух таблиц с множеством столбцов
очень кстати полезная штука будет, особенно если можно без всяких макросов и ВБА 8)
Да и в Способе 2. Сравнение таблиц с помощью сводной в 2016 Excel можно в одной сводный таблице получить значения из разных таблиц. При этом не потребуется копировать две таблицы в одну.
Подскажите а если строк 3000 на 2 листах одного документа и я делаю объединение запросов и неожиданно эксель говорит что не хватает ресурсов. 6 гигов оперативы, интел кор i3
В чем дело?
Причем в результирующий запрос рисует почему-то 5млн строк, откуда он взял столько?
Приложите файл.Расскажите, какой тип слияния используете (добавление, объединение). Если объединение, то какой тип (левое внешнее, внутреннее и т.д.)
Всё это лучше на почту или на Форум - тут такие вещи неудобно обсуждать
При объединении запросов, после разворачивания правого столбца, содержащего "микротаблицы" получившаяся таблица содержит в себе две сравниваемые таблицы с весьма странной "синхронизацией". Количество строк в итоговой таблице значительно превышает количество строк в сравниваемых таблицах. Исходные (сравниваемые) таблицы имеют по 5 столбцов каждая и 200 и 220 строк соответственно, а таблица после слияния имеет более 1000 строк. Строки в итоговой таблице дублируются по 6 раз (закономерности не нашел в повторениях). В чем может быть причина такой "синхронизации"? Наименования в строках должны быть уникальными? Без повторений? Т е если есть две и более позиции "лук" с разными ценами в сравниваемых таблицах, то такой способ сравнения нельзя использовать? Извините, если описал сумбурно или вопрос сформулирован слишком "по-дилетантски".
Обработка, сравнение, анализ прайс-листов поставщиков, на предмет меньшей цены.
Ну типа берешь два прайса и он тебе сверяет наименование количество и цену.
Загружаете прайс листы поставщика за 2 разных периода и после их сопоставления
вы увидите все новые позиции.
Заранее благодарю!!!!
В случае с большим количеством столбцов, не совсем удобно в последствии просматривать результат, приходиться крутиь бегунком в лево и право и перепрыгивать фильтром, как вариант можно объединить не только первый со вторым запросои, а так же второй с первым, а после соединить их (добавить), в результате получим по ширине таблицу в два раза меньше, хотя манипуляций больше, но кому как удобнее!
А как сравнить две таблицы, если текст ячейки совпадает частично.
Например на вашем расмотреном примере, совпадение по какому то частично общему признаку.
Кукуруза и кукурузасвежая (написано слитно)
Общий признак в этом случае слово кукруза
я раз в месяц использую ваш метод с Power Query уже несколько раз удачно сравнивал 2 таблицы , спасибо большое . но сейчас не получается - на этапе Слияние кнопка ОК не активна . что делать ? не пойму почему, помогите. Спасибо
[IMG]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAB4AAAAQ4CAYAAADo08FDAAAgAElEQVR4Aey967cdxXX26/8kccbJGO+Hc8b5fD6dd5zw2id28CGJE0exHY8QJ3Ycx9iAwQZjGwQYYowBCwMmRkJCXCQM6C6hC7qhC5K4CAFCAiQhCQnd0F3autUZT8vPYu7a1d3V19Vr7afGaFV11aw5Z/2qeu1eNdW9PuOUREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEhoLAZ4ZiFBqECIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiAUwBYi0AEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEhoRA4QDwmXMj7s3d29yTa+e5nz43yX1l0rXu//zxVe5PvvcX7k/+8/8ZEiwaRlMEzl+84Oa8sdbdOmeq+/YT9yU5zlFfNV177bUu63jnnXeqmhjT/6WXXnLf+MY3HHIklHkcOHDAvfLKK+6Xv/xlUved73xnTP8qFVffu9h94ZZZ7sTpc0E1YFFX+uTjk+7xm5a4uyfM7B2o81OdNn3dOhcBERABERABERABERABERABERABERABERABERABERABERABEcgnEB0A/va0ie5//tfV7rM3fN599oefd3963efcn177v9yf/uAK9yfX/EUvAJzUof6Px5//8C/drc//Nt+TFAkbcCpSTlFXqPrggYNuzqw57oXnXnAL5i1wJ0+ODXgVUtiCMHyEr/AZvmMM/UwMyE6cONEdP3nC3Tn/ySTwi+CvPX4x/0l37sL5Sq5mBR/RdtNNN7m6g8CTJk1KgrvIkRD8RfrZz37mduzYkZzff//9ydqpc/289t6BJPj793fOdzNXbk9s+v9k8fBl885fuG+te+Sa+YnYzjc/ToLATQeAuXbS8k2bNuW5XVv7pfNn3ZFNj7gDK2/rHcffnVWbfikSAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQgboIRAeA/+xHf+k+e+P/mxsA9h1DUA9B4LKJQd/Y/kXl0/QeOXLEzZ09Nwmkzn5htjt06FCaaOfq4St8RhAYY8BY+pUQdGWa9fqaUUFfBIDvWvC023FoX1KP9iopK+CJNgR/6wwCI6CLgC9zPPHLp38RAOb5li1bqgwr2PeBWa+7O5/e4B578S33vYdWBGWyeAQ7ZFQuf3JzEgA+c3LEtRkATnMJY7v11lvdxo0b00Rqq7908bw7unmqO779cgCcihEMVhIBERABERABERABERABERABERABERABERABERABERABERCBrhGoPQCMJ3+R+AQwy2UHXjSgW1Q+5NexY8fc/LnzkwAqgqi7P9wdEut0HXyG7zgwFoypH8kGgH/ywmOjAsDXzXjYHT553D2+5sWkHu1VUlbAk20IAt988821PAk8d+7cXsAXgV+eYwy//e1v3eTJk5N2vAIaqa4ngPHKZzz5u2DDTrd97yfJk8DI/cQx+/VlzhH4ffqOFb3XP+M6a+MJ4DRfOTYEgfGa7arpzL5X3YFVd/Se7rVP+qJ89K2nnbt0aZQZBYBH4dCJCIiACIiACIiACIiACIiACIiACIiACIiACIiACIhAHwisWbPG+Ufdbvj6Y87r9qEf+vLGWbdPsJeWstpCfQoHgH/87H1uw44t7s9v+IL7Hzf+ldu2f6dbsHlV7xXQISMMCofa8uqKBnSLyvv2EaTjK5QZQPVzBFSXL1vuNr+xubagnu9HzDl8hQ/wxQasfX9xvmB+f15hbQPA//Hkb9zvVs5zb+75wH33yd+4N3a/71Zse6MXFEZdlcSgYJYOyPDIkotpQ9CXv/3L3wLmE8DIEZjcunVrL0hc128AI/CL3/61B54E9lMMD79P2jmCvfd/c5ZbN3trZ54A5jzWMU4Ec88efDtt+MF6BYCDWFQpAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiLQEoGsAGWdLhQNPhaVr9PXOnVl8a17jNaWP4asNl+W54UDwF9/9MdJ3+898Qt387P3uwsXL7rP3fXNXgCYwd5BfQL4xIkTuQFgG2DFq5a3vbuNPFvLt2/b3nvNs/UnrYygNsbWdJo/f767/vrrkyArbDFId/ToUYcnfL/75ANu674P3f5jR5JXPyPoy98CrvMJ4IsXL7rly5e7e++9N/EHOc5RT7+aZtGU/pumrEle/0z9CP7iiWA/1REYpU4EfhEA7soroOkX8jrGWSaYW6aP9VtlERABERABERABERhmArNmzRr1UzQvvviiW7duXatDxtt/4EfZhL72gL46k8+oTt3SJQIiIAIiIAIiIAIiIAIiMD4IMDDI0fIceZ3J6o0t12m/X7qyOGa1lfXXsqWOUB3bsvLCAeDP3vB59+aebW7d+5vdzoN73R82vuj+5Jq/6AWAQ8YYFA615dUVfaK3qHzIPn4zd86sOb1XKH+468NRYiMjI+7ggYNuwysbejL79+0fJWNP7OSwbNuLlmGLgV74AF/gk03wmTIYS9bvANMnm1tdRcoM/oaCci++tTEJ9v7gmd8mQeCbnv99L/iLIDDaqyTaRJD3wQcfTAKDU6dOdYsWLXLI0Y56tFO2ir0iffHU7q3T17vzFy4HoIv0tbL7jpxKnvyFPia+BnrVlr2sSvK6xoigL4K/Cx/dlOjtwm8A24HWMU4bzD2zb1Pm66Aha4+jW56y7kSXb7zxRucf0Z0lKAIiIAIiIAIiIAIdJ2CDmwj8vvbaa616zIAz/Cib7BjK6sjq17T+LNtqEwEREAEREAEREAEREAERGE4CdcR5QmSg10/nzp1LXj3tx6cgF5L3+3f53HIMlZscY8heGZ6lAsDfevzWZF7OXTjv/u87/mlUAJjB3rqfAF7x1Ju5a2H9nK293yjNFc4RQFAVT/ciiDrr+Vnuo70fBXu88dobicyqFauC7ay0E8a6sjlswS/YDiX4Cp8hgzFgLHmpLv8QjAsdt99+uztz5oz79ZI/jAr68ulf1KO9SmIgcPHixclTv2+/PfqVvjhHgBrtbaa563f0Xtd81zPVgtxF/CaPIn2qytZpM1ZXrFzW2BgAvjhyolDwF/0Orb0nS7XaREAEREAEREAERGBcEmBwE4Hftp/8tcAVALY0VBYBERABERABERABERABERhmAnXFeUKM/AAkgr7W3tmzZ0d18+VHNQ7AiR1bqIwhNDlG32YZZKUDwHj1M47/dde/jAoAh5xgUDjUllfHJ3qL5nl6Y9p3f7h7VCD1wMcHxnTDIkegFU/Z5qW6FgOfTg79rwr4aAPXGENsqsM/BOPSjocfftjhQ+Clra+7exbNcNfNeDjJcY56tFdJDAQi2IwnfkPpiSeecGhvK9ng71fuXODwtG7VhN/jffymJb3/7IBrA3V+Ig+/vsr51fcuToLZJ06fC6qp02asrli5oMN/rGQA+NSuFaOe7rVP+qaVj701I0u12kRABERABERABERgXBJA4BWvTF6xYsWY8TM4zAZ7bst8hTPfZoQ2HtSLnHWhQDPayib0pW3qwJPFfJqZ/rENOdrpz65du5Im6GAd2plC+tmmXAREQAREQAREQAREQAREQASKELABwyL9YmX9+JG1x7LV5cvbtkEoZ/nPNuZNjAe67VHGRuEA8P/2o7907x/Y7Wa//pLb+8nHbsHmVaMCwAz21v0EcD8CwDFAGQCeN2dejHgtMrCFoDMer+9aQjAu60Dwde3ate748eOJ68hxjvqqgTz2v+GGG9yyZcuCaFCP9jrTyLkLQXVNBH9h6IX71rpHrrn8m79tvY4Zdl9770AS/MXvDc9cuT04Zs5BsLFgZayuWLks80kA+NIFd2jdvYUDwKc/KvdUt//6Z5wriYAIiIAIiIAIiMCwEGDAk0FQOy4/8GnPbZnBVAZhbZvVx3KoHXVlE/raw/oBnfCPdThHMDoUhLZyCBpTJuRvWV/VTwREQAREQAREQAREQAREYHwTqBoszKPnBztxjp/bRH7hwoUxT8P68nn6s9qhK+/I6l+mLct/60sZ3Xl9rH5bzuvntxcOAN84895Exxd+9e/uztm/S8pf+tV/NP4bwAgA5yUbJM6Traudr4Bet3ZdXSpz9cBW1iugcxU0KIBgXJWjimsMBCKYPH369KAq1N9xxx3BtjKVR06cdd99cLl78qWto7rPXvdB77XPePL3/X1HR7VXOVn+5OYkAIzf5m0zAPzArNfdnU9vcI+9+Jb73kNjn+TAmDgHVcbHvrG6YuWoN5QjAHz24zcLB3/R78KpsW8GCNkI1dkgcKhddSIgAiIgAiIgAiIwqAQQ3ETwNxTktEFVlhlIpTyCpHzC1m+zTChDPX7AGfWhBJ3sQ5u+XFo9bSJnoj6eMycDa4tPL6fpZ1/lIiACIiACIiACIiACIiACItAVAmkBUdZfunRplKusH1VZ8sQGQdPKJVWndsvyP6stVWFkgx0fu4Tq2JaVFw4AP7riWfeHTYvdn173Ofd/3HSVO3D8sFu5dWMvANzkE8BZA0FbWwFgPHl78OBBt+GVDb3f2T16tL4AX944YYuveYYP8KUrTwPjN3YRkLNH2ngog3aUqz4BCR1I8+fPT37r99133x1lmr8BfNddd/WeQB4lUOLkx5Nf7gV6n15+2V6TwV+4iMDv03esGLXe7SugycHPSwyv1wWvfMaTvws27ExeY/2FW2aNep21b4vnPQUlCrE6YuWyXEAg95PXHyscAD607tdZaqPaqq77KCMSEgEREAEREAEREIGWCTC4yWCpNc821tlzlNEnFCS1cujrB13xpG1sAJi2s3LfHmU5ptgAMPwKpTT9IVnViYAIiIAIiIAIiIAIiIAIiEAWgbJBwiydti0t6Fm03urscjltXPA5q63KmKCXh6+H9UVsFw4Af/aGz7vP/vDzSQA4ec3zD64Y9Qpo36lzF867P//hX/rV0eehoC7rfCWsR95UQqAVT9/yWDB/gft4/8dNmUvVC5uwTT+QdyEIvHLlSvfTn/60UAAYATz0WbVqVep4YxoYCASHBx54IPEBvwW8dOnS5DeB0c5j4sSJSeA8Rm+WzN7DJ93Xf7moFwS+dfr6XnnCXfU++Us/EOy9/5uz3LrZW4NPAHOMNmffsjkCvwj62gNPAjNZWyyzrWwOPTEpVi5LFwLAZY5jW5/LUqs2ERABERABERABERi3BGxwE7+Zy4AugNg2/xxt9pXJVtaW0Q/BXurlk7ZtBIDhB/1OCn/8B37z94FtPeRtsJht/nhYr1wEREAEREAEREAEREAEREAEihIoEyAsYsPqjy0X0d812bwxNuUv7KalrLZQn9oDwPztX+YI/t76/G9DtqPqQkFd1vkKWN90AHj+3Plu9crV7t2t77rz58/7brR2DtvwAb7Apy4EgP3BZwXnstp8PTHnVh/ePY/f+73nnnuSoC+e+l20aJG77777ekHgn/zkJ+69996LUZ0ps/vgCffVuxeOCo42FfyFIwj8IgCc9QposOCR6Xxk401T1iSvf6Y4gr94Itgm2rPzYNuLlmP1xMpl2S8T/EWfM/tfz1KrNhEQAREQAREQAREYtwT84CYCtXwS1m+z5yjbIKrfxtdBEyx0Qob66w4AQzcP+IUy/UPOMdEfyiKnLwxOs02/AUxaykVABERABERABERABERABERABJoiEB0A/va0ie5//tfVrugTwFUdXzXzrVGvurVB3qxyVbvqXw+BrOBcVlsZ6zH6ECSfMmVKLziKJ4/rSDv2H3P4rV88Idtk8BdBXwR/Fz66KXG7jd8A3nfkVDIuPAXMtH3vJ0ndqi17WZXkMXMwqkPGCXTFHhlq1CQCIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiAC44pAdACYVM6cG3Gvf7jVPbl2nvvJsw+4Lz/wffe/3/il3m8AU065CIBAXgCvTkp5ttgOmwsXLkx827TpciC1Dj/e33fUffuBZQ7BYCUREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAER6AeBwgHgfjgpmyIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAvkEFADOZyQJERABERABERABERABERABERABERABERABERABERABERABERABERABERgIAgoAD8Q0yUkREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAERyCegAHA+I0mIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIwEAQUAB4IKZJToqACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIhAPgEFgPMZSUIEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEBoLAZz573efceDj+7PrPD8SEyEkREAEREAEREAEREAEREAEREIHhJLBlyxanYzAYDOcK1KhEQAREQAREQAREQAREQASaJjBr1izX5BHr/2c+e/34CAAjyK0kAiIgAiIgAiIgAiIgAiIgAiIgAv0igOCvUvcJaJ66P0fyUAREQAREQAREQAREQAS6SqDJ4C90xyYFgGNJSU4EREAEREAEREAEREAEREAEREAEKhBQYLECvBa7ap5ahC1TIiACIiACIiACIiACIjBkBBQA7sOrp4dsDWk4IiACIiACIiACIiACIiACIiACA0RAgcXBmCzN02DMk7wUAREQAREQAREQAREQgS4SiAkAL1u2zG3bts198sknbvfu3W7t2rXRr42OHbOeAI4lJTkREAEREAEREAEREAEREAEREAERqEBAgcUK8FrsqnlqEbZMiYAIiIAIiIAIiIAIiMCQEcgLACPYe+HChTGj3rlzZ1QQeEzHlIq+BoD/ftK17sipYw6/z2vLOG/iSGGgahEQAREQAREQAREQAREQAREQARFonIACi40jrsWA5qkWjFIiAiIgAiIgAiIwzgmcP/mxO75tjkOuJALjiUBWAHjx4sXB4C/5vPbaa7lBYMrm5X0NACPIu3jLmp6Ptz7/20YCvwwm9wypIAIiIAIiIAIiIAIiIAIiIAIiIAItE1BgsWXgJc1pnkqCUzcREAEREAEREAERIIFLF9zhDZPcgZW3Jbm7NPZpR4oqF4FhI5AVAH7//fczhzsyMuJmz56dGQTOVGAa+x4AZnC2jdyMW0UREAEREAEREAEREAEREAEREAERaJWAAout4i5tTPNUGp06ioAIiIAIiIAIiEBC4NSHq5PgLwLAOE7t/vRBwDxEDz/8sLvmmmtGic2cOXNM3SgBnUQTuOKKK9zEiROD8mCPdvw2bVZC+4QJExIRW87q06+2mPHU7VtWABi/+ZuXVqxY0Y0AMBzF65vTArg7Du5xOPz2UL9Xd76djNvqw1PBfrLtvt6sc19P2XMsGHtwoUMfJsa2hRYXPrz8DzD09ftBF1NID/v4F2Oafsj5Nvy+tNdG7vtix0v7YEs5csb4WGdzfDgxpTGw8ihbmzi3PGDP/yBM00u7beb+WKzv9CPNX8sVemzCuT9utvt/AHwf+IfYr8e53xc6qzK240AZKWt9+H4VYYa+IXlbb8tkBpa23pYp49f552lyrO9HnuYjfPE/B+21iXb0tYflivqY9QedmGubuP5Y5/thfbZlyiNPq7cyTZfBA37YwzKC/bRrO81/W2/Ldiy23pazZCDHA/z7legDc8uLdczpJ86tHHz369iHeVZfv7/9fEJ/m3w7aAt9VtBuSN5f33nXmf17R1/qXkd5YyA/2m8ztyxRtjxCfP2xwNeYa7OfY/LXM3xJm+O89Wl5FdFr+6Hsf55nrVv46vfHeej+AWNDG32zZc6BP4e+DBj4/rFvm3naHMFfe/hrNtQGXf5nAa472khr88drdaOMflz/ZO73iTn39db5mQDdVXyD//AHemyy69LnZ+WKlMsGFv3vua/temeU2VmvLhv1nfvnzz/Ya//r+7/nHlr2TO8cBehDHyaUIcc2a499bR3KrKcOm6PNyn97yq22OWnzxwB51tm+1lZaPXy3Y4Yx+MAxjTIecVJ2niJUS0QEREAEREAEREAEhp7ApfOn3cE1vxwVAMY56mOTf4+Pe3P7vShWj+TGEuB3s9B3KO4XhNp8TfiORF1dnht/LfnjaOI8KwB8+nT+dbBu3br+BoDx271+8r+M8Xd9IesHbdHX1iHQS522/vHVsxwCw9Tt92N9TO77W/Y8a8Fg48BuJvmyuHBwEeHwLyIryw0y+mjbWIfcr8/Tbzda/L5Wbxtla98fL8aBdusv6ux5aPyoy2OAdiTfpvUHc+hv8mTpTRS2/I/1F1ywpmxK8xfjtmPDWPEHlAl6rW7WI/f/AKTJsY/fbs+rMMbYoMuuB9TZc/hg7fnnRZj5fTk+v963B9YxzPx+/jntpdWzvY2c44EvPKxdcPX9RB+75my7Pw/Uifn0E22zzeqBrH8jCN1pn8d+X9pKq2d7GznWjX9NcsywjzJY4LD1aEvz39bbsh2PrbflojJWvq2y9Te0pnxO8Mv2oZ9+nX+eJufXx3zOWp/yPiv8MeHc9y3rOoN+yNtU9zrKG4O13Y+y5eXzsG3wLTQW1mddm22Py/rtrxH4kjbHGJ/9TA7dB3B9FtELm9Ynn0fMumUfX49/7tvy20NzaGVC9yC03WaeNkf++LLWrG2DPozTJnw2QCarzcr7tv22Kud2DqzfVXSyr9XNuiI5OGFdWH5ghnXLVNUG9ZQNLOL7LoOjCGz+X7f9I1UmgU7bjga0MyAKeRuAZbCY7ZBHmee+Lhqy9dTBNptDj/UPbQjE2mCs1cW+ts6W2Y7c1lsfwAZtNsEHyJRJZeepjC31EQEREAEREAEREIFhI3Bi+7xe8Peqq65yOPAUMOpjE7638rsrvzvF9pVcNgF8twl9L8b3H34vAvNhSXV9lyvCIysAfOTIkVxVK1eu7F8AGE/0MigLTxGwRaAWCV+6eOD3fe3Ben4xs4Fe6KQOW8/+7Et7PC+SJw7W8E/WgrEfTDDly7KduXXHl7XntpzVh3qZUza06ZOmk32azn379hwbrHbDJc0X24cyHDtz1iP35e05y+iHDzo/UR9zv73tc/pLu/45/WROOT/HBhw2vZigJ/YPgG+TOpj77TyHT1UYl10ftJ/mH1kxpxxyvy/bbL0to51+2npbDumItcW+beYYD+eN4+CGPv3AWvKvXf/zh33Zx56jHLv+7DyFbgRtO2z5dkI3MlaG/rWd82aLdn2fOC7mlEPuy7LN1tsy2/2+VWSszrbKvr/23JatP6F6v84/Z/+i9aHPWbv+Yj4rrM2q1xnGwfXDnGNDbm2l1fsyMWOwutou+/7ac1uGX6GxoD7v2uzSmOAL55Z5mn9569PnQ33MrV5f1rbFrFvK+3r8c8jZOltGW2gOKQO/+beM9vqVkyFz6wf9ZZ09t2W023OMjX+HMbdgwZTVRhlfn62vWrZ+1m3H113WV+hJS2AJplVT2cAivvcyAAwf7DkCnQjy2mQDoijbgCwCtAgI24AsygyWWt1Wp1/vn0PW2rV9UbYB2VBfW2fLVo9fb88xJnLAWOz4rI6Yctl5itEtGREQAREQAREQAREYZgLnT+5zB1ZNDAaAUY/22MT7c/tdBn39+397zn1I1HHPGznO7ZGnB/f/lLffIVFmPXK7vwOd+H5n2znWNH1WlmXqtPrxPc+eQ68dF7+r+DK0b3PIQB65TfzOY3Vk+U0/fd9sf/hIfqinLMpgxWTnjXJsQx4aa5E+0ImDPlt9bLP2/PKNN97o/MOXsedZAeCtW7da0TFl/Abw3Llz+xMA5iuZ8UULBxIDtgziso1P/vLpXtb7/RD45WuirT7IIdCMdvb121kfkyfO1vCPXSi+urwPIywsLDJcYCjbZPXiQuCFARnbltYH9Vn60Qa9TGk62d50bu3b8fLCjbFvdVA+i4GVtzbRF22ow4daKGXpDck3XWfHAlv+eay/GK/9sIWe2D8Avk1/zH47zqsyrrI+Qv7wQx++ZzHz+3Kstt6W7ThtvS2HdKAuJJNVTz1N5v6asD5iDWG8WXMDttARGofVhbJvC31gg/V2ziCP5H/2hup8O1ZPoiSDPdvbyP2xWL9hv851asdj7dhyURkr31bZ99ee27L1J1Tv1/nn7F+0PvQ5y/UX+1lBm2WuM9iw9xQYR53rKHYM5NePnPxg2+fht2G+kGw9zvOuzaRTi//4/vnnWXNs3cxan5AroteXpZ3YdUt5X49/7vtl27PWo22jrX7mWXPkj8lew1lt+FsJvUj828kxZrVRBrnVn1YPGfBEjsPeS3K+UU9ffL3oa9vS+mAMtGEZWHlusKAOybZZG9ADHcjTUl4bbaT1j6kvG1jE991QADg24IrgK/sjMOr3g34m31ao3n8KmTKoTwu8IkCb9ZSxtWvL1I3c1vs+IOjLQLcNaNv+seWy8xSrX3IiIAIiIAIiIAIiMKwEPnl9ci/4i6d+7RPAOEd7bOL3cP8+Hef23tye4zsA2/C9w36PsHLwIe+cflKO3zX8ep77uf+djO3Uh3Nb9s9tG8Zlz6Hbji2km3V+Tj3ki3Z8X4ROJLan9fNlfN/YH/owB0yopw2y5FxBB2X9trSx5vXh91T6w71l+uOPw9aHyjYAHGq3dVkB4Hnz5rlTp05Z8VHlN998MzP4C92x6TP4AlXk8IO5MMQAMIK1eGIX+nw5BINRR1u2X1oZsggMp/Wjrtg8FkqeHBdMSA6LEQuJycraTRe0Y4H6spDnQR3IWRfKeZHk6adNq4N9ra22ytYPlJn8cbA+lKOfHYPftwxjOye0maeXcm3mduz4MOOHJ3zI8xft5M8PQvpOvTF/AKiDuZ0L6KMuqxt1VRj7Y6PuUB6yTx+LMo1MSUoAACAASURBVOMYQzl1WnsxZfpsZVHn2+AfP1+O/dvIfe7WF6wV8AQHXHOhZK9F29efB7bFrD/YoRz6+Snr8xjy9ugCY/oPVlxTqCMTlP15sFwpa8dly9Rp6/xymkyIT1pfjqPNHL7Q99Casr5Szvahr36d7Wfb/Hp7Tv2YK9bDJ5t8XeyTVm/HBNnY64z2kdtU1zrK89vat2OzvrRV9n2xdq1vaWXIZ12bVl9bZeurXSOwnzfHseuzqF6fM9d+7LolOzs21IE9P4dwjrKViS1DDmPvQsqbI/hqD+uzrUfZT/xybO8NKZPVRhlfP5mh3l731M/1xP72WsFc4W81ktXLvnl92M7+tG/XBNaZ9S3LPtek1WvL0BNKvNcJtRWtKxtYxHdeBnARRGWQFXUMevq+2Cdu7dOxlGeQ1H9a1v9+Tbu2nvZ9mwjKwlYowe8iAWBrL9YH+AX7af6F/ArVlZ2nkC7ViYAIiIAIiIAIiMB4IXD24zdHBX8R8L3mW/+YHCjzgFxMwv0/7tH5nYJ9UMfvKajj9wF+N8E5D/vdg3JWD+WY8zsHv3eyHrrpj+1PedYhh7/oZ30M6YMs5KwOe84y9LE/ZH0/rG30sYdtY5l64R/50IbvE+1SJ8dEHezHc/aHXv/7l5WBHGSgHzrRZhPb0sZapI+1S720ZdtYl5UjCByTsgLAaIP/oSDwzp073ezZs/sXAEawF4lfxlBmANg+AWyDwZBFYJivjcY5+/lyrKd+PkXMc7+d9TF5YrSGf7IWhd1wgCkri4vBLnqUUcdkZbmwkft6KO/X5+mHLvjHZO2xrs3c2rfjZTnGF6sD8nkMrDztIEdCGz84WEcf8vRSrs0c/vKw8wofiviLdQg9TChj/GCBD0Tqw4cxEtv9ctLo/WNlKV+VMefNMxU8DdlHHY6izHxdNGjrWfb5s54M/PVl230Zy8uXow9t5D536wv/cPoy1i/wxliQ0JeHPw/UG7P+oIs2wdxP0G1ZUzd9YFtXGHM8vO44Huu3v7ay/o6wvz9eqy9GJo1Pmh6rs60yfOGRtqZ8X0L++3X+OXUUrU/7nPXn0+pFmYcdE9c8fbE55Ox1xjXOPjz37VZZR74ufwy0af3sR9n65fNgW9ZY0Cfr2uzXmEJrBL74Y/Hn2PobWp9l9ZIl9JMz1iTL1i7Ldt2yzupBHT+H6BfGZ2VY9sfNeuhAmXrgT7+T76s/R9Z38qPfWW2WF+/d7FjJINRGOaufdchtvS3bNupHOw9eO+zD8VB3Vh/4ST3IIYvDfi4WtU+7oRw2/AT/MT91pbKBRft9lwFc+ITAKNpCyQaAGZhFsJcBWgZkmVMH9DHgyjrkrM+ySTu2H8uwWyQAXMYHjA9+wo8qqew8VbGpviIgAiIgAiIgAiIw0AQuXXCHX3mgF+RlsPdH3/u6u+G7XxtVDzl36ULUcHHvz+9C7MDvsfa7AmRC3xXYBznkra60c/87i/3e6tu2+qwtlPFdAt9psvSl+UB/0T/vO5W1a/X53zspZ2Xoo/2OxfY8v0O+0W/og32bqJd1tM3vhKxHzjbfB8oU6WPtUi/12DbW1ZGnBYAXLFjgNm3a5BYtWuTmz5/v8L1jz5497sMPP3QbNmxIAr9og8yLL76YGgiO9bHwE8D4MoVAL4O5MIQAMH+/F+040pJtRx8EeFnHfgwoI89qt/1iymk+Fa1PWxRYjPZCgV4ri3LooH0rizosRixkXw/l/fqQbtQx+Re8b49ybeW+fTtecMQHSF7ydeA8dFCPL29tsg12UbYppNOXsfJtlOlvyFZRf60uW+YHol3Xtt2W0/zAdcFE+aqMq6wP6w/9Qg7fQgdl6DvPmdt6lDE2y4u6adfKh3T48jiHPv5Rox72bTPHeuAfbo7Dn0v6av2Cz5BnYl+e29y25a0/9oNNnwvOi8wD/bb2qb/NHDeR/iaz9Qnl0EEfrSzrkNt6W46VCfFJ02N1tlXO8iWtLVTv1/nnHE/RevSzfVAu81lB+5wPniPPu878v3fwwT+oz/rKOuS2HuUqY7B62yhb32HP55E3lrxrs40x+Db8Mdl2tIUOK2PLVpctWxmUQzpRx+T35ec42mPWbZoe1tvc2kI5bw4pDzmU+53gQ+igX/SX5/6atX/3bBvl/f6sR57VltVu+9my7YP7Fcx1KNk+9ppK6+N/rnENheSpO9RGXyjD81AOGZtCbG17mXLZwCK+74YCovDBBnrpkx+kxTnkEIBlcJRP/vJJYPZNs2Xr/aAx+/p2WY8c9jkG32e/n7Vlddj6NB+sjO1bpFx2norYkKwIiIAIiIAIiIAIDBOBUx+uHhXkZQA4LYd8XsL3Bu5FZsnae32U8b0vlKwc2tPO8b0C3wWQUIYcciTUU7/fPxEw/0AWY8jS5+uw5yjjexC//9k21EO3n6yMHw+irJXhd2Sri+15fqf5xv6wb+cP9bRDrnZs5MrvgmzLGmtMH/rj2wQPtpFNXbkfAMZv+u7evbun/vz58+61114bE+BF4PfcuXM9uQMHDiTBYl9fTyCnUCoAjC9UCMz6CfU47G/6sg65fUKYfe3rnSGDxACw/9Sw3251x5Rps2qetiiweO2Chh3KYiHyQ8PaT/vA8Bc59di+VfTbvr7Ots7tmPzx8oMHFyUTyrygWWd11MkYc8n5itFLf9rM7dit3Tx/MTbLFfLQxWT1so0fzJCx7bbM/jb32+15Fcb0y44jb334vls/85hl9bVjQhmH9cvva+Xpg19nz6EL574e9m07xx9c+GMP6wPnhn+g6XfaGrJ9Kcu+1JXVF23+5y70hOotV1vuEmPrF9mwrs51Ssa04bOnTdSn8bEyVk8/ylm+pLWF6v06/5xjy6vH+rOfA1zLtj90WBm0Wb22zH7Mqc/OI+TTrhXIUV+d6wg6y46BY2kr5/hhz/LAOdrKjMXqbGsc1k6a/bw5jlmfdm3RZp5esmRfn3PMuqWttLGx3bcFeRyx6xEMeJ9ndbZVrsrS8vE5cwxWhnXMs9ogk9Zu623Z74M2jNFPRftgPjlPKKM/59iW/bUVa9/3j+NgPfSG7jHYXjYvG1jE910GT33bCOj67Tjn07aUR9DVBmFRj3PI2uTrYptf759TDk/6Qq9NfDUz6/zXNOMcB1Oabr/eP0f/UB31xuZl5ylWv+REQAREQAREQAREYJgIXBw57g6+fFcwAPyDb3/V/ee/TnD7V9w6qh3y6BdK+M6G+3rsQ8YkyPK7KL87oA6Hvae3ctCbdc49UHwnQRl6ocv65PeHTsigHoeVDenL8wE60vZ62Je27Hcl1iEPJdSTF9qtn9TL9iy/03yz+tGf+lFv+djvjfxuCxkcHA/9Z71tK9KH/Tkuq9evY1uV3AZs8UrnI0eOBNWdPHnS4bXPOEKvhEan48ePO/xusNUZVBaoLB0AxpcqHEgM2LLOBnpZh9wGhtGPTxFbGepjgNnXzXbbJ7aMvnUkLBZ/UfBC8Ospiw8Ku6DpB+q4scFFyNwucuphP+asz9Mf2uhiX+pqO+c4mdvxwhewZBtycrJ+op7M8xign9WHsrVpdUEW+jCvMXqtT22VfX9pN89fjNnnwL7Ifb38gKaMbff12A/9kC7bF+1VGBddHyF/OKY8Zll97ZhQtjcV1O/L4Dx0cC37bVynVg919yvP8gWfa3YM/mdfVl+/LW39Ya1B1m8HD9T5elBv61C2RxcYW39C5X/7t3+L+jvCdWTXBvSx3pazZKwPIT62HWX/+re6my6njQl20/z06+25ZWXrOUbUUcaOjfUxn7MxnxUhG7QXc51Z3zmH/fy8Iz+Ooc3cskCZPOADzrPmw+/rn2fNU5NjhB8h23lzHLM+y+glS8vH//zPW7fklTY2ttMW/YR81hz68jjnPYjV2VY5b47or2Xpr9m0No4hi2FWG22TLfX59b4Oe+6vMc6NlYE+fCbw73haH/5N53yRg11L0G91p+myMnZctgwZJviHc3twLJQpk5cNLOI7b1oAGH4wCMzvxnzK1/qIgHAoMOv/Xi51MGcg2fchpI/20Mb+zPHEsU0MPqPd94t9mBfxAX2yWFkf0spl5ylNn+pFQAREQAREQAREYJgJHN/6wqjgrn3q96qrrnI4bB3L6Kc0fgjEfCdrgkY/7Npg7caNGysPC99PrM5YhZUDwPxCNgh5LBTJiYAIiEDbBPrxh6jtMcpeNoGsNZDVlq1VrUUJiHVRYsMvn7UmstqGn4xGKAIiUIbAeA0s8rd56wjOluFetM94naeinCQvAiIgAiIgAiIgAiBwYNUdwQAvA72p+ao7BHAcEejXHko/7Npg7Y4dOyrP8scff6wAcF4QujJlKRABERCBhgj04w9RQ0OR2pIEstZAVltJc+qWQkCsU8CM4+qsNZHVNo6RaegiIAIZBBRYzIDToSbNU4cmQ66IgAiIgAiIgAh0nsCZfZvc0TefcEdefTT6gDz6KY0fAv3aQ+mHXRsAPnz4cOVJxuuhrc5YhXoCOJaU5ERABERABERABERABERABERABESgAgEFFivAa7Gr5qlF2DIlAiIgAiIgAiIgAiIgAkNGwAZrz5w5U3l0Fy9eVABYTwBXXkdSIAIiIAIiIAIiIAIiIAIiIAIi0BABBRYbAluzWs1TzUClTgREQAREQAREQAREQATGEQEGgGfPnu0uXbpUy8gXLFjQCwLHKtQTwLGkJCcCIiACIiACIiACIiACIiACIiACFQgosFgBXotdNU8twpYpERABERABERABERABERgyAgwAL1y4sLaRLVmyRAHgrKeAayMtRSIgAiIgAiIgAiIgAiIgAiIgAiJQkIACiwWB9Ulc89Qn8DIrAiIgAiIgAiIgAiIgAkNAgAHgFStW1DYa6KLeWKV6AjiWlOREQAREQAREQAREQAREQAREQAREoAIBBRYrwGuxq+apRdgyJQIiIAIiIAIiIAIiIAJDRoCB2nXr1tU2stWrVysAnPYE8J9d/3mHL3E6xEBrQGtAa0BrQGtAa0BrQGtAa0BrQGtAa6Bfa6C2HQApaoxAv9aG7OpzSWtAa0BrQGtAa0BrQGtAa0BrQGugrjXwmca+MUmxCIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIhAqwQUAG4Vt4yJgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIQHMEFABujq00i4AIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiECrBBQAbhW3jImACIiACIiACIxXApPfWuB0jGUwXteDxi0CIiACIiACIiACIiACIiACIiACIiACIiACTRFQALgpstIrAiIgAi0S2LVrV4vWZMoSEHtLQ2USCK0LBX/HBn/BZLyn0FoZ70w0fhEYVAK6ngdj5jRPgzFPWV5qDrPoqE0EREAEREAEREAEREAELhNQAFgrQQREQASGgIA2Qfo3iWLfP/ZdthxaFwoAKwAcWrOhtRKSU50IiED3Ceh67v4cwUPN02DMU5aXmsMsOmoTAREQAREQAREQAREQgcsEFADWShABERCBISCgTZD+TaLY9499ly2H1oUCwAoAh9ZsaK2E5FQnAiLQfQK6nrs/R/Cw6DydOn3GLdn4npv4xBp35c9mJQfKqEObUvsEis5h+x7KogiIgAiIgAiIgAiIgAj0n4ACwP2fA3kgAiIgApUJaBOkMsLSCsS+NLqh7hhaFwoAKwAcWvShtRKSU50IiED3CXT1ej5//rybNGmSu+qqq5Lj6quvdtOmTXPbt293aBtvqcg8vb5tj/vy7XPdF26ZFTzQBhmldgkUmcN2PZM1ERABERABERABERABEegOgcYDwD//+c9dmWPv3r3doZTjSZnxoU/Xxjgs48B0lR3Lnj2D/+W97Ni7th5zLrtamhfMXeBKHQu695uVXdkEufK2ha7No5aFUFFJHezTNhWr1lccWuvdm1o7rQ8k5ekiBYAVAA6txTo+Q0J626gre88xDPdbXeY7Hu/p2piPGBtdvJ4R4L3jjjt6wV8GgW2O4PDmzZvdmTPj42nWmHm6ePGie2TOq6OCvhPuWuBumbrWfe+hFaPqcb8GWfRRaodAzBy244msiIAIiIAIiIAIiIAIiEB3CbQSAC46fGwmPfDAA50LkKaNA/4WTV0c47CMA3NRdiz33XefG/RNybJjH6Rrruj1liaP4O+Z42cKHegz+4XZbkHHgsBd2QSxATzL3dbbclUZ279f5TrYVw30pvXvF5Oydu3aqLNc1p8q/ULrookAcJ2cYnQ1MYYqnNEXf/faPKr66/cPrRVfpqvnZe85huF+q405Kct3vN3TrXxppcPRhdTF6/mFF17oPfV7/PjxBBNyBHxDgeHrrrvOLV261B08eLALSBvxIWaeXtywvRfk/aufzXZPL3/XXbx4qefPoWNnkmCwvQfDK6GV2iEQM4fteCIrIiACIiACIiACIiACItBdAp0NAB84cGBggsBlN2e6NsZhGQcut7JjwUbHoG9Klh1719ZjGx+bZQPAh/Yf6lwQuCubIH4ACfPo1/nnVWTaWCd5NupgbzcP6yzn+d61dn9t1HXej3GG1kUTwdO6GMXqaWIMVecHf/fy/J8zZ04tMmX+xuaNL7RW8vp0pb0MD/QZhvutNuagLN/xdk+nAHD2auSTvmkBXTz1i1dB45XQlGWOV0UjgIz/IDtMr4rO+9w9cfJ08ju/vCdD8Bdp/5FT7qG5m920pVvd6ZHz7vyFi6OeBsbvA584dTp1QiZMmOCuuOKK5EBZqTyBvDksr1k9RUAEREAEREAEREAERGB4CHQ2AAzEg7J5UXZzpmtjHJZxgGuVsWBzBE9ODOqTwFXGPijXXF0fwWUDwHhqOAkCz+rOk8Bd2QTJC8LU3V7XWqiipw723GCsO68yrn70/dufP+++fCuOF3rH3/z8eVf16MdYQuuiieBp3ddUnr4mxlB1fvB3L89vBYCrUg73r3LPMej3W2Ei9dZW4Tuo93S4NytygDgDwEePHi3UF3bqTqHP/rptFNXHYG5sP3wHQtAXTwKzL3MEiYfhVdF58+Q//Xv89EiCz776+dEFW5K6BRt29p4Uxn1c6Cngbdu2JUHfmTNn9qYBdfa816BCFIG8OYxSIiEREAEREAEREAEREAERGHICnQ4Ag/0gbF5U2Zzp0hiHZRxgWnUsg7wpWXXsg3DN1fW5XCUA3LUgcFc2QWLWHwIxeSlGJsZWnp062utgf+2116a6ksUiqy1LZ6qxPjdgYzktZY2nbFuarTrqQ+uiieBpXuCz7vYmxlCVNz4L8saJa6UOmSY+d0JrpSqTtvqX4WH7DPL9VhuMLatYe7bPIN7TxdybIdA7c8ZMt+v9XQkWGwDG/dmMGTPcyMhI7k98KACcv6rwqmi8Djr0qmjUoY2vlc7X1h2JvM/dGx8d+xu/35n00qhA79LXdycDenbVp6+KRgD45sfGvo78mmuuUbC35unPm8OazUmdCIiACIiACIiACIiACAwkgc4HgEG165sXdqMldhX4fbowRt+nmLH4fbowDvjt+1VmLIO6KVnH2LsyjzHzVkUmZpPR/41gv09XngTuyiZIzPrLClpyPmNkYmxRX5N5HeyzAphZLLLasnQ2yaOK7vvvvz+1e9Z4yralGquhIbQumgie5gU1625vYgxVceOzIG+cuFbqkGnicye0Vqoyaat/GR5+n0G932qDsc8qxqbfZ9Du6fz7LP8+DOdIzz//vFu/fn1SZgD49OnTSR2eXkUK9bV1CgAnmKL/waui8fRv6FXReFoY3CEzCCnvc/evb5szKtjrv6EFT/0i7T54wn317oWjZL929+gny/n0bxYXvhba5uiHhDo8Kcy2hx9+uKcKgWXWT5w4sVfPOuSQYcI59eIV1OyTpof9upjnzWEXfZZPIiACIiACIiACIiACItA2gYEIAANKlzcv/I2WmEkM9en3GEM+5Y0l1Kff44DPIb/KjGUQNyXrGnsX5jFvzqq2x2wy2o1ClEN9uhAE7somSMz6ywpack5jZGJsUV+TeR3sswKYWSyy2rJ0Nsmjiu6bb745tXvWeMq2pRqroSG0LpoInrZ5HcBWE2Ooiht+4Vpo42iCd2itVGXSVv8yPEJ9BvF+qw3GIVZ5dkN9BumeLnSf5d+LgQGCvnPnzk1wMACME9ThHMnv558rAJxgKvUPfg8YvxuMoC9+J5iviEZ5EJ4IzvvczQoAz1h5OTC79/BJ9/VfLhoV/EWgeMKd80cxXbFihcv7vV8bmEVne26DuAwmM4hrDfl9KIN6JspkPZFMGfbpap43h131W36JgAiIgAiIgAiIgAiIQJsEOhsAxuZF2nHp0qU2GeXaCm205HVKGxvr+zHGYRkH2A/TWPLWkt8+nsfus8g7j9lkDG0Wol/a0Y9rF+PsyiYI1l8bQRjYKLPW89ZEmfY62GcFMDHWtJTVlqUzTV+/6+FzzPH9a693OGJk+8UhtC6aCJ7mXQe8Hjm3Vc5hq4kx0LeyeR4D6M26Vmg3RibGFvXF5qG1Etu333JleKBP1tGvv6P9ZhmyPx75xtybgRWCvC8tecktXLCw9xvAKKNOAeDRq4nB2dG19Z7hd4P5muhJkybVq7wBbXmfu9c/snxMYBfBXTzte/HiJXf05Ij7xj0vBmX8V0AzaJs1DD/oas9tGTps8NY+GQw5BJuRUOZhf2cYdehvnyKGfJqeRFlH/8mbw466LbdEQAREQAREQAREQAREoFUCnQwAZxEosxGSpa+Otrp9qltf7Bjrtlu3vthxQK5u23XrKzKWorJ1+1q3vqLjaVI+ZpPRDwBnnUNfv1JXNkFi1ktMkCVGJsZWG/NRB3sEKTFme7Th+yDauHjxontkzib3yJxXHcpdTaF10UTwNO864JoipyrnsNXEGOhb2TyPAfRi3HkpS+bs2bMOx+OPP56npnB7aK0UVtKnDjHsi7hWt74itrsoWzePuvU1wSzm3gx2Fy9a3AsC8wlgBn/RhpR1z4a2Ju7bung91xEAvnDhglv75k5399Nr3ZU/m5UcKK/bssuhDQlPBddhK1HW8D9587Rw3bZgcPd7D10OsG7c9nGwHUHiFzdsH+M9ngC2gVhfAIFZPrGLNntuy2hjANgPLMOGDQBTn1+Pc776Gfqy9Ph+duk8bw675Kt8EQEREAEREAEREAEREIF+EVAAuAbydW+m1K0vdoh1261bX+w4IFe37br1FRlLUdm6fa1bX9HxNCkfs8mYt3lo25vYSIwdf1c2QWLWS1aQheONkYmxRX1N5nWwT3tK1f/NubrOm+TRpG48GThj2ZbepivKXX1aMLQumgietnkdwFYTY6i6ZmIYxHympMkg8Hvu3Dm3ceseNzIyUtXdMf1Da2WMUEcrYtgXcb1ufUVsd1G2bh5162uCWcy9GQJpGzZscIsWLOo9/csgMOrQBhl7jxYqN3Hf1sXruWpQ9uCR4+77Dy3r/e39y1tmORy4J/niT2e56x5Z7g59cjxZDlVtNbGmQjrz5unEydNJkDt034UgMI5QG4Lj6OsnPmHLAC3aUWZQ2A/y2nOU+cQu+rANZQSDqQv11E8ZtPkBYAR8EQBmEDhLT6K8o//kzWFH3ZZbIiACIiACIiACIiACItAqAQWAa8Bd92ZK3fpih1i33br1xY4DcnXbrltfkbEUla3b17r1FR1Pk/Ixm4yhDcO0uiY2EmPH35VNkJj1khZksWONkYmxZXU2Va6DvQLAcbOzbsvOMRuueCKpiym0LpoInuI6wPXSxgFbTYyh6vw1yWD16tVuZOScm7zoTXflbQuTvO4nz0NrpSqTtvrX/Tlct762ODRlp24edetrYtyx92YInG3atMktmLegFwRGGXUxwV/cyzVx39bF67lKUHb3/sO9v7s/nvyyW/fOPnfw2Bl38OgZt/btj9yPH1vdCwTv+fjI0DwBjLWd9hQw130oABx6+pfyfNIWwVkcDN6i3QZs/XO0IVjLfgwaQw7BXeryA72UT7MDeRxZepLGjv7TxWuto6jklgiIgAiIgAiIgAiIwDgmoABwDZNf92ZK3fpih1jV7pkzZ9zJkycdcjwt089UdSy+73Xr8/XXeV63r3Xrq3OsVXXFbjKmBXz9+iY2EmPH2JVNEKyXNgJRsNGVtVkHewWA41b6o3NfG/MEMOq6mELroongaR3XAa6nmARbTYwhxnaWTAyDmDH6MriXwStNz46cczf8/uUkANxEEDi0VrLG26W2GPZF/K1bXxHbXZS1PBDYfOyxx5IAZ1lfrb6yOpruV+TeDIGwN954w82fMz85UI4N/ioAnD+T+PybcOf8JMD7+4VvBjtcuuTcYwsvv5njq3ctcFf97d8nQeCgcIcqYz53L//kxKu9ADgDvhwGz5k39dMUCOTydc60rdy5mDkUJxEQAREQAREQAREQAREY7wQUAK5hBdS9mVK3vtghlrWLDVIcJ48fcp/sfcMd3rHSHdoy3R3aeI87tOG/kjLq0AaZNlLZsaT5Vre+NDt11A+Sr3WMt4qOIpuMfrA3dK4AcNzT936QJTSHMTJdWet1bEApABxaBWPr3tmxL/ndX262YnP2nR37xwp2oCa0LpoIntZxHcRcb0AKW02Moep0xTCIGaOVwX0NXvs8dfEWt3Xnx27k3Dl39zMbkiDwVRMXuo8PH6vqdq9/aK30GjteiGFfZAh16ytiu4uylse0adOSADByJKzX2INjs/pY17W86L0ZAr5btmxJjiLBXwWAwzN/xx13JAFc5Kve2JEEP7/7m8Xu4sVL4Q7OuQsXLrmbJ19+EvjKb906NAFgDvj1bXvcl2+fOyYQzHsRtEGmqaQAcJjsIP/tDI9ItSIgAiIgAiIgAiIgAiJQPwEFgGtgWvdmSt36YodYxi5+exEbpIe2zXOH1/00K7TbcwAAIABJREFU7ti+INal0nJlxpJlrG59WbaqttXlK55ywjHMqegmYyjoa+sUAFYAuOz1ggCwv5EPXWmBYbTZYJVvN6stS6evp2vnCML5CU8odTGFNiabCJ7W8ZnP9eKvQXsOxrDVxBiqzl8MA44xyxZlbPCXfwsRBL5w4YL73bw33Pt7DmapKdwWWiuFlfSpQwz7Iq7Vra+I7S7KWh7j+QnguubG3rONpwDw8ePHHY6YxNdFI//xfy93X7xlltu8I/8/8L6541Dyu8BfvP6xoQsAg9up02fcko3vuVunvtwLBKOMOrQ1mRQADtMd5L+d4RGpVgREQAREQAREQAREQATqJ9DpADCe7MErhU+dOpUEGTF8bMp1LdnNmTp8q1tfrE9l7CIAjHTo7afigr/rfuoOvfVMrEul5cqMJctY3fqybFVtq8tXbnpX9afL/asEgPfs2uNmPDPDrV+/3h05ciQZJvN+jLkrmyAx649BlixOMTIxtrJs1NVWB/u0oGxaPXzPYpTVlqWzLiZN6cHrns+OjPQ2X89fuOCeXBJ+LWVTPsTqDa2LJoKndVwHWevFjhe2mhiDtVGmDL8whjoO/uYvnvzl30Hmb+/Y73jfU8bPtD6htZIm27X6OtYfx4R7/rOnTrhDG+e4C+fPJwfKqBuvqU6+YFi3vibmJXRvBjtTH5/q5rwwp9SBvkjjNQCcNk/2aV/K2AAwXumMAPCpM2P/8xXlmZ84fS4JAH/hJ88NZQCY41TeHQKD/LezOxTliQiIgAiIgAiIgAiIwLAT6GwAGEFfPNXz0cFP3POr33VX/3qJ+8JPZyc5zlHflVT3Zkrd+mI5VbF78tiB5PXOR3atv/z651fv7wWED716f1KHNrwC+tihXbEulZarMpaQ0br1hWzUVVfFV2xsYwMWiRvedfnVRT2hTUZ/czB0/uyMZ93evXvd3Llz3eTJk93MZ2a6F/7wgpvx9Aw3ZfIUN3/+/OQ1tW2OuSubIFh/dQRhYnRUWet1zk0d7NOCsmn18B+M0lJWW5bONH1dqf/VzPXuh79b3gsAT1n4hkNdF1NoXTQRPK3jOshaL5YtbDUxBmujTDmGQcwYEfzla5/5N5A5XvuMJ38PHqz36V+MN7RWynDoR58Y9rF+4f7j2J5tbt+9n3P7n7ouOVBG3XhNdfIFw7r1NTEvoXsz2GHwd/GixW750uVRB2TZDzr8ezrYqjt19XrOC/aSgw0Af+XOeUkA+My5/DdtnDjzxwDwTTMVACZM5Y0S6Oq11uigpVwEREAEREAEREAEREAEChLoZAD4xIkT7ty5827yojfdDx592d01Y5P75bOb3OmR8+7uGRuTc9SjHXL9TnVvptStL5ZPFbt4/fOhd2e5Ywfed2dOHXfnzWs6z50bcadPHXNHP96eyEC26VRlLCHf6tYXslFXXVlfsemNJ+wPfnI8uba46Y3rDHXDmEKbjP7moH+O35d77733kidRpk+b7mbPmu12vbcr2VR8f+v7btZzsxzq8bTJjh07WsPWlU2QmPUXE4iJkYmx1cYE1ME+LSibVo9xZTHKasvS2QavKjZWb778e4T83T3kq99o7zor4ntoXTQRPK3jOuB6QZ52YOyw1cQYinANycYw4BhD/VGHv38jI5d/85d//5gz+Iv/nHjnnXemqShdH1orpZW13DGGfYxLuPfHf/w8eeijJAC87/F/d8lx7+eSuhgdwyhj+Y73V0AjkLts8bIxQVz/Ps2enzp2KumDvki2DeXxFAC2gd0zZy6/stjW8fqxdT+bujoJAL+58zCbU/MtOw8P9SugUweuhr4RGOS/nX2DJsMiIAIiIAIiIAIiIALjjkDnAsDYXDt95qz7jwdXuideetd9cuKs++rdC5PgL2YHQeBv3POi2//JqaT9W79Z4UK/CdjmTNrNmTrs1q0v1qcqdqN///ePvxMc61NZuTJjOX36dPK68ZGRkcQsNiKxQYInUm677bayrrTer8zY8eQvNr83bt3Te/KXG9/M0TZsqWgAGE/+fvDBB+6pJ59yz/3huVEbib6umTNmJnJtbU60ZSdvDcSsv7xADGzEyMTYyvO3jvY62KcFZVGfFpArW59mqw4WTevAZ9WMZVt6TwCj3MQreesYR2hdNBE8reM6iLnewAS2mhhDVd4xDLLGiL9/+E9Q05e+NeZvoA3+4qdJYmwVHU9orRTV0S/5Onnsn3uX2zfpqiTwC9Y4kiDwpKvc/tm/6NcQ+2rX8p02bVriC/MifwM4CKuPdV3L/fspBGqREMRds2rNqHsvP6AbOkcfBYBd8lQug7ucc54jZ7J1K1//IPl7+/2HX8r8W3vx4iX348mrE9krv3WbngAmTOWNEhjkv52NgpFyERABERABERABERABETAEOhUAxkYPNuBufWK9+8dfLnXTl293kxe/7R6ZP/r3/XD+4NzNSTvkHp2/2Qyp/WLdmyl164slUsXuIAeAse7wHw9OnDrtJs16zf1/ty1MNoD/8b8Wu4WvvOcuXLjgjh07Foux73Jl5hFBbjzli41uHKs373Rnzp5NDpRZf/jocP0OX2iTMbR5iDr85u++ffuSJ3ufe3Z08BftIV34jeDHpzyerKGmF0ZXNkFi1l9WIIacYmRibFFfk3kd7BGU9Q/4nBWszWKU1Zals0lOdenGZ/ZDsze5h2ZvbP1V60XGEFoXTQRP67gOstaLHTNsNTEGa6NMGX5hDGUO/uZvVvD36NGjyav9ob8O3v4YQ2vFl+nqeVke+E93fkKQd99vvuT2T/1Ocm33AsCoUwDY6QlgBYD9a6bIuQ3ssl9eHb6X/93t85LA7mOLtrDbmHzyosv/MWvCXfPdVV/+BwWAxxBSRRMEBvlvZxM8pFMEREAEREAEREAEREAEQgQ6FQBGEOqDvYfczVPXu50fH08CvF/5xUL31V8uGfVEBs5RjwAx5BL5jw6FxtdKXdnNrzTn6taXZsevr2J3kAPACP4ePHLc/cPdi919L2x2b3/4idt98KRbt/Vjd8u0V9zPp61vJYDnz0fZ87Lz+Os/vJpcZ6+8vXuMadThSeD7n391TNsgV4SCtmkBYARzFyxYkLzeOSSTpguvg16yeEnjmLqyCYL1VyYIU6ZP2bVe92Q0yT4rWAtmaSmrLUtnmr626uFbzPH9a693OGJk+zXe0LpoInhax3XA9ZJ1HWINwFYTY6i6vmIYcIzWVt6Tv7gnxT0CApFMMbYoG5uH1kps337LFeUB5ni7Cpjitc9IyMmYr4BGEBgHfgMYdeM1FeWbx6lufXn2yrSH7qegR08Al6H5aZ+8YC8lfbmdHx3qvXXj+w8tc+u37nefnDybvKVr3Tv73I8nv9xrn7zg9d6TxtTX1XyQP3e7yrRtvzSHbROXPREQAREQAREQAREQgUEk0KkAMJ4GeGjO6275m59u9PzzvYvd7oOjnzrcf+SUQz0T5NGvX6nuzZS69cVyqWJ3UAPA2NjF70j/869fcg/OfWsMKrxa9P5Zm90Lq98d09bViiLzyNc72zz0SnXUWRmWu8og1q/QJmMouIu6l19+2U2ZPCX5zd+QTJqu52Y+56Y8NiXWpdJyXdkEiVl/oUCMP/AYmRhbvt4mzvvFPotRVlu/AqIx7LN8a6ItxqeyMqF10UTwtI7rIGu92PHDVhNjsDbKlGMY+GMsE/yFbzG2io4htFaK6uiXfBEeeKMK7qsObZrr9v3+ajdy9nIgeOTM6eQc9cf2bEuCvvufus7tf+bGpIy68ZqK8I1hVLe+GJtFZUL3U9ChAHBRkqPl/cAuWmPqcM1+6evfdV/80fReoPeLt8xKfhv4C7fM6tWh/MWfznJXfucXegJ4NHqdNURgkP92NoREakVABERABERABERABERgDIFOBYDxm6tX//old+iPv/UEb/924jx39OTl32Sl9/gdYNQzQf6b97/E09bzujdT6tYXC6SK3UEOAC9/bYf79wdXupHznz7hY5lhvX39V0vdzn2H3ZmzI+7EydO9J1WsXFfKReaRgVybKwB8Jvj7ch999JF7avpTbtd7u4LtoQ1LBIpf2/Cae3L6k40vj65sgsSsPz8QE4ITIxNjK6S77roq7K+6fVHynysmL/70P5mcOXfB/WjK+t5/ukAZdX7KYpTVlhVI9W20fZ7lWxNtTY4vtC6aCJ7WcR1krRfLCLaaGIO1UaYcw8COEcFf3HOmvfY59OQv/YqxRdnYPLRWYvv2W64oD/xnzwOrpiWB3X0P/q3b98CVLsnv/VxSf/bUCXdo4xx34fz55EAZdeM1Wb56BbReAV3lOogJ9kJ/qtzf/J3D7/ve+eSaXtD3F0+tdas373BPL738CmgGhBEE7noq+rl76vQZt2Tje27iE2vclT+blRwoow5tSu0TKDqH7XsoiyIgAiIgAiIgAiIgAiLQfwKdCgDj9W82EIUyvkj6daH6v7l9Ud9o2s2ZOpyoW1+sT1XsDmoAGE+jXPfoajf3lV2ZmB6cuyX5beBfPLPRfes3K5LXkm/d+XFmn341lp1HvQI6HPjl074jIyPu2ZnPBoO/kEEA2B7st+uDXW7mjJmNL4eubILErD8biEkDEyMTYytNf531Vdj/070vJX/jvv3gquTJOPoVCgKfPDPi1qxZU/kV21mBVNrvV57lWxNtTY4ztC6aCJ7WcR3wekOedoAVbDUxhqrzAL/S/Pbr8Zu/+F3LrOCv/c1fv38dvP3xhtaKL9PV86I88Prng+v/cDkAfO/nRuWoVxpNwPKdNm1a0sjcX5tZ59Rq9bGua3noP9TBRz0BXG2mUgO7V1016ondPDk8ERw6nlr6Zi8wjO/vi17ZXs3hhnsX+dx9fdse9+Xb544aH4PdyNEGGaV2CRSZw3Y9kzUREAEREAEREAEREAER6A6BTgWA054AxhOYNukJYEujvnKVTaFBCwBjAxLH6TNn3VW3v+je3Hm4EMh3dn/i/unepW7fwaOF+rUhXGYe8fvbBz857q6auDA5Vm/e6c7gd/rOnnUos/7w0eF6Cie0ycjArZ/v27cveQJ4+9btqUFgvw/OX1n7inti2hONT31XNkGw/rI2oetsK7PWm5iIKux/9fwbvf/kNHXZ6NecnhnJfhIYLNNSVltWIDVNX1v18K2Joy3/rZ3QumgieFrHdZC1XuyYYKuJMVgbZcoxDDDGKk/+0q8YW5SNzUNrJbZvv+VieeCeC/f5p48fcfvu/XwS+D2w8nF3fN8H7sDKqX8MBH/enT52pN9D6pR9y3c8PQFs/0MdykgIAC9bvMydOnYq+j4MsuiDvki+XupOGmv6p6vX8x133JEEepEz5QV7s+SOHz/uJk2a5LZvvxzoRVB40rOf/h4wXgeNp2O7mmLmCf85/ZE5r44J/P7d7fMcDhsERhmy/D3zro57mPyKmcNhGq/GIgIiIAIiIAIiIAIiIAJlCHQqAJz2G8D4zV+b9BvAlkZ9ZbvJVFTrIAWAsc7w5XzDO7vdtyYtd0+tKPc/1Je9sdfd+9ymoqgaly8zj9i0wcb4xq17esEo/8l7tA1bwsZfKGgbqsNvAE+ePNnNem5WdB/owVPD+O3gplNXNkFi1l9MsClGJsZW09yhvwr7XQdOuC//YnHvuvvWpJXuJ9M29I7rf7+u14Zr0r4OOotRVlvXA8Bpc5bld9m2NFt11IfWRRPB0zqug6z1YlnAVhNjsDbKlGMYLFy4MPe1z3jyN2/zPsZW0TGE1kpRHf2SL8Jj36Nf//SJ38nf7L31APcg+yZ/89O2R7/er+F0zm4RvjHO160vxmZdMgji4li8cLFbvnR51AFZ9qvLjzw9Xb6e8Z8wbKoSFN68eXPvddHXXXedW7t2rbvu+h+6v/rP+3qBUQSBF28o9z3L+tlEOWaeXtywvTcWBnsff3Fz8rcELFFmPfMuB72b4NhPnTFz2E//ZFsEREAEREAEREAEREAEukCgUwFgPIX4/p6D7qbH17kPD5xwT614z33lFwvd1+5ZMmoDHOeoRzvkIL/zo0N941n3Zkrd+mLBVLE7SAFgPIWy8o2d7jsPrnQbtx90l2IBeXL7PzntvnLXYq+2/6dl5xGvxEQQGE8CT170Zu+aQxl1w5iKBIBnPDPDLVm8xE2fNj06AHzy6Ek3/Ynp7qWXmv+N8q5sgsSsv5hgU4xMjK021m1V9q9/cMh97VfLetec/58v/PN5Gy6/sj6LUVZbVrC0DV5ZNrJ8a6Ity5eqbaF10UTwFNdBm0cTY6jKOuaz4P3330+Cu/j5BntN4Q0X/M3f+fPn57oSYytXiScQWiueSGdPi/DY97uvfRrkzQoA/+5rnR1v244V4RvjW936YmzWJTP18am9YC6DurE5+raVBvl6BqPYp4Ihi6d/Efy1fRAEnrrw9VGB0bbYF7GTN08nTp5OfueXgV3m23Z9+hNAKLOeOX4f+MSp00FXVqxY4a644ore8fDDDwflVBlHIG8O47RISgREQAREQAREQAREQASGm0CnAsB46gJBqJ9OXe++ds8yN23ZNvffC99yD83bPGoWcD5pzhtJO+QenT+6fZRwCyd1b6bUrS8WQRW7gxQAxjr7p18tdavf2heLJii3/aNj7h/uHp4AMAaJp3DwHzGQuEEeHPyQVBYJAO/Ztcft37/fPT7l8eQ3fUNPCft1Tz/1dPL0L7g2nbqyCRLzOZIVnCSnGJkYW9TXZF4H+1Nnz7s5r+xyE59+1f3g0TW9A78NzGsR+TW/W+OOnz6XDCeLUVZbViC1SU4xurN8a6ItxqeyMqF10UTwdBh0lmXMfvgsyDpuv/12h99xn7p4izs7cs4xCMzg78GDB92dd96ZqcPqp9268tBaqUt303piP4d7r4A+djjnFdDFfpKj6fH1W38s31g/69YXa3c8yQ3y9Yx5in0q2M4pAsF4AhhPBePJWNz38jeBn166xYp2ppw3T6GnfxHkvf+5jb0ngFFm4NfmoaeAZ86cmQR+t2379Oc+JkyY4BQELr8k8uawvGb1FAEREAEREAEREAEREIHhIdBKANhumuWVly5dmvwuK57OfGble+7oqRH3jXtedPwdYOT/fO9id+Do6aQdciPnLm+G92ta8sZUpr0fYynjJ/ogdTEAnDYevAIaAeAlr1d7pfHDC952D819ox9TlWkzbdxF6mGAQadMYwPeiABwkWPKlClu7969yW8B44lgP+DLczz5+/TTTydP/+K3g9tIXdkEKbLO6pBtg22ejabY4+/djZPX965FBH+Pnjzrpk+fXvl3cvPG1K92BHmbOPoxntC6GIZgbRNjaGN+9h06mlxL1/5uVS8IjCd/u5BCa6ULfsX4UPRzHDoPrv/Dp08C3/u5XvngumdjTI4rmaJ8Y+SHEeBzM5/r/c5vv8c3yNdzGjv7hG+azKDV583TjY+uCAZ3baA3rXzzYyvH4ECwF0FgmxAMxhPBSuUI5M1hOa3qJQIiIAIiIAIiIAIiIALDRaDxAHBZXOfOnU+e7P3Boy+7u2Zscvc8u8kdPTni7nx6Q3KOejz5Czml/hM4uu8dd2jDL3IDwZCBbL/Titd3uG8/uNLt835fOsavcxcuuufW7HB/f9did+zE6N+njuk/KDLjIQBcdi4QBMaTwE888YTDpuOm9Zvcrg92uVfWvpL85u/0qdOTJ38/+uijsiYK99MmSGFktXVogj2eCL5h8qe//2uf/K3NcSlqlEBoXTQRPB0GnY1OxB+V3//8q73/TLFmy67kCa427MbYCK2VmH6DKnNg1bTLQd8H/9bte+BKtw/5vZ9zqFcSgSIE0l4BXURH3bLDeD2Hngqum1vb+vLm6a9vmxMMAP/wv1f1XEU5FAT+2t0LejIoZAV6ERjGq6H9ZF8VzTKfHsY5nyhG2T5FTFvsY4POrEN+zTXXJCZRTtMFGfaZOHFiz0Xbn5XwAfUcS4yM9RUciqa8OSyqT/IiIAIiIAIiIAIiIAIiMIwEOhsAJuxd+w67385+3f3dHQvcF26ZneQ4R71StwhcOH/enfhknzuye6M7vHONO/TOzORAGXVog0wXEl5Ntv7tD913H17Z2xBmwDMmf+CF14Y6+NuFOeq6D1hDS5YscVMem+KenPakm/nMzCQgPGXyFLd8+fLW3dcmSOvIewbrZo/g7w8fU/C3B3hAC6F1MQzB2ibG0MYU42/79KVvOfyuY9dSaK10zcc6/Tm0aa7b9/ur3cjZM4nakbOnk3PUK4nAoBMYb9fzoM5X3jxVCQBPuHP078kj0JkW4MwKADPgC8YIqPLcBlcZRGUb9DHo67dZHZy3LF2USbPPYC/aESy2Y6HeLBnI02/4bIPM1nZaOW8O0/qpXgREQAREQAREQAREQATGE4HOB4DH02RorCIgAiJQloA2QcqSq95P7KszHEYNoXXRRPB0GHQO4/wXGVNorRTpL1kREIHuEND13J25yPIkb56uf2R58OnemCeA/VdAMxAb8scGTW27H6y157aMPgi+IoCKYCvabGIb6vx+oTorb58MRl8Gc1G2AVvU4wlgO5Y8GfoKOR6wXSTlzWERXZIVAREQAREQAREQAREQgWEloADwsM6sxiUCIjCuCGgTpH/TLfb9Y99ly6F1MQzB2ibG0OV5bMO30Fppw65siIAI1E9A13P9TJvQmDdPC9dtKx0AfnHD9jEu2+AoG7MCwwiK8ulYyNtzW0Ybg7YMqlK/bfN1UCZNl++b9Z99UIeEJ3chX0QGvrI/fSma581hUX2SFwEREAEREAEREAEREIFhJKAA8DDOqsYkAiIw7ghoE6R/Uy72/WPfZcuhddFE8HQYdHZ5HtvwLbRW2rArGyIgAvUT0PVcP9MmNObNE34u4MqfzRoTBM57Ahh9Qj81wKdp/aCu/f1eO04GWVlnz1FmPwZ9qRdtsIXEIK5tY9nqDemCXj6RSxvIkegL+iH4S7lQADhPhr7SnyJ53hwW0SVZERABERABERABERABERhWAgoAD+vMalwiIALjioA2Qfo33WLfP/ZdthxaF8MQrG1iDF2exzZ8C62VNuzKhgiIQP0EdD3Xz7QJjTHzFHoKOC8AHHr6l/4zCIwAqg3Ust3mDLKyzp6jjMArchw2iMqgL9sYtIUe1IUCwGm6ENBFHwR4Q8Fd6qSNojIMLNNX+FEkxcxhEX2SFQEREAEREAEREAEREIFhJKAA8DDOqsYkAiIw7ghoE6R/Uy72/WPfZcuhddFE8HQYdHZ5HtvwLbRW2rArGyIgAvUT0PVcP9MmNMbM08WLF90jc14d9RRwVgAYsujTdAoFcsvarFNXWR/K9ouZw7K61U8EREAEREAEREAEREAEhoWAAsDDMpMahwiIwLgmoE2Q/k2/2PePfZcth9bFMARrmxhDl+exDd9Ca6UNu7IhAiJQPwFdz/UzbUJjkXl6fdse9+Xb544KBH/hlk9fD402yLSV6gza1qmrrfHTTpE5ZB/lIiACIiACIiACIiACIjDeCPQlABz6osFXD/mvJRrECena+Or0h6+Vwiue+pXqHE/RMbQ1/n6OsSiTtuXxW1Jpx969e9t2pzP2qm6C9GvNtXVNNTlRsez5Kj2w7udnaF0sOHcYDw/UxSb2HwYWoTGH1oUNnpJZKP/VwinOyg572fKz1wnYjIcUWitNjxtsQ9drWn3T/vj64Rs/G2zZl+vaeeh6Zl2Id9f8b8qft956a9S927Jly4KmcB+He7ypU6cG2wehsh/Xs+XC9RbKx/MatIxQLjpPp06fcUs2vudunfpyLxCMMurQ1mbC3NY1l3XqapNBmTls2z/ZEwEREAEREAEREAEREIEuEOhEABi//8INv7q+zPQTrv9Fqt/jq8Mf/kYPN+PGG9+2x1/HnPVzjpq0jY3BUKA3rb5JX7qku+hGlu9722uu7WvKH2+d53ns8XcNfP3faLPndfrTli7MIX4XjslfQ6z382Gae39s9jy0LmwgF7xCgd60ett32MrkhrWBz3Im/OdAu8ZYP2x5aK00Pca06zWtvml/QvqxFuAPDqyNQUhp/NLqB2FMVX1ct25dcl3bezcEeG0QmAHiQQ78klM/rmfaRp621tLqbd/xVO73PI0n1k2NVXPYFFnpFQEREAEREAEREAERGCYCnQgAY3MPG+HD8sXUH0e/x1eHPxxDFxZ/HeMpOo62x9+PMRZl0i/5tEBvWn2//GzbbtVNkLbXXNvXVJPzkcd+mMZqOeLvNgJ0TP4aYr2fDysPf5yhdWEDt+ClAPCC5Elnnx3PEfTrwn88oz9N5aG10pQt6k27XtPq2U95NoE0fmn12dqGoxVBXQSBbeKTvqx79tlnx8iwbdDyflzPllHaWkurt33HU7nf8zSeWDc1Vs1hU2SlVwREQAREQAREQAREYJgI9D0AjA1kbAYj8Yup/R//qBu0xHHA7y6Mrw5/oMPOC8pMmD+042AwwMqingnl0FPeafXsZ3MrW5YvdPDg+oMNPqmHNrvpjHM7Jjt+61tdZdgjp7JjhC8co9WHMnSyjWPBeFHPZDfeKYucvFC2PvIceqiTdqizjhy67VMk1GnrubGIOhz+xiM2I9mGp06YsAHJeuS0Y/X5T6eE5G1f6Lbntuw/FZNlhz6m5VU3QTh/0F9mzWHeocMe0BX6fEA95MCC8ijbZPtBhmvNlrm+Qm20kdZGW1Yf64rmWexhHzbyUpnx8qcToN+Ow5Zh157bss+PvkLGfv6l+Q770MFkdVtdqPfl0ubecuDfE44BenBAxibbJ80HOx4rQ92hdVKVT2hdFA0AI0DMcSO/YdLE3quhcc4A8pe+/NfuX374H0nbhH/9Rq8P6/7zjh/16tCPflgdrENu61HmAd2UC9mBH5Rl7utjf5vb+bRlzK39bLBznbY+aBdzinm3a8/+XYMd+7nFNvZn7q8Ruy5s/zR5O560cmitpMnWVQ9/ue6tTlufxhvydux57MgMuu0kl2tzAAAgAElEQVR85n1O0D/257n1EX5wLdh6v48dY5Nl64O1Y+vTuEKGfqNsWWX1QZtN/HzFvCBZzuCFZOcPtnAgZfmANs5BIvzHf9Lq0cz7GivPMu6neA8Gn/FEMHKWKYdz3o+hzp5TP/vZ+z3WIcf9HZPtb+/D7L0h+/r2qCMr78f1bP1Jmw9bb9cE6rHumKwc16Odd7t2uMZsH3tNUidyyPDw16yVa6vc73lqa5zDbEdzOMyzq7GJgAiIgAiIgAiIgAjURaDvAWD7hdGWOUB8QeSXS9Z1PbfjSCtzDG2ML80HW5/lDzcJsBnChL52s8DW200C1NsxhmxCJq2eem1uZdPKlLe2WYfc78c2bFrQf4wPm4pFxk89VXPfP/pk62kjbYzog/Eg2X4oow8Sx4Yc42U92jB2zrHtn3T0dHIzyPoJOcuT/armduPO6rL12MTjJiA3B7l5iE3AefPm2a69MvpRztfHeuhlf9ShD5KVt+WsNm42Ure1b+30HMwoVN0EsXOcVqb5tDWHdtuX8szZxnUHTkxo43pDnV077Id6Ww6tO65BX9b2o01fxtYXKWexZ2AkT1/R8ZIh9drx2TLa7bkt+/ysD/z8o/5QbuV9O2jjfNJX5CxnzT1tWV/9MmWQWz+snK2347Eyvt+2Df39c/iPZPUlFYF/QuvCBj2hmwHctHoEVBn0ZTCYfdgfgVjKWD0oU8bWQ/7W6fcngdxQu9/PyqBsdbFsZfz+oXP2Y27x4ZqBPhx2nVgZlNHO+bBl24Z5Svu7hnoGDrN0W30o++vCbw+doy4rhdZKlnwdbWQcysnV2rGMi7LjHPD6p36wDH1OwK615zNnG/Syf14fO5Ymy/TNtxFTD5k0Vlaf1cU+9rsSdIAZ61Amc/+zy+qCDepD2Z8vX5Y+pdWj3d4nUZ457nkQAIYMrnX7Smic8z4OZd4noa89hw7KUQ9lrRzKTLbevw/z9YfOqSct78f1bH1Jmw9bX/baw9oKfW5St39NpvkF+X6nfs9Tv8c/DPY1h8MwixqDCIiACIiACIiACIhA0wT6GgDGF0j7hZxfHjFotOGcmxdNg6hTP8fRlfFV9YcbQJYRxoYDCZtJsMGDcxaaQ8owpyzOuTll7YTKlK3Cl/aRc/MQvth6lLGRkTV+trFf7BhC47J10AddVcaI8XCOqA82bBnndrMGG0JMtuz3sXpgg2uA4+c52VJnHbnduLP6WM/fkbNtfLUgNwdtmy3bzyNfH8558EkS2GIwmPLQRzmb+xuS6IdNS/aj37YP7Vgf08pVN0E4x1XWHHyjHvrJtYB6HFiXvG4ogxx2uV6ph+1WJ8uhdce2tH5o51Hms4d6/TyLfWisfn+cwy8mOw6W/fH6eilHXTi3B69Nyvn60j7/6JOfQx8+O2yibuqybfyc8f2GDHzBgRRaL6i3Y/E/V9DG5Ptg+9FfW8dy3XzgT2hdMOCZFRSFTwjyIkiLsu1jg71owzme7rUyCAZzXMgZ7MXTwPacPoRkUWcDzZSxgeY0O9TL/jynDuTWX5TTEj4PIc+UtT44h5BFH57bv2Ush9Yhbfj97bl/3bCPtUd51PGgXFoeWitpsnXV+z5Tr60P8S7Ljvr5WZD1OQFZ+hFijjbowfqwKauPlWuyTB98G7Y+xBXyVgbnZIVyVh+08TMUXMEFax1lcoZuHvwsDNnM8oH9mUN3SEdS+cd/su67/ACw7Yd7JHt/Ze+NUIZe3jfZfrzfQ53twyAx69Hfvw+jHuq351YX69PyflzP1hd/DtnGeq4J1iO3a41y/rWXde2jT+iatDYgwwNrtt+p3/PU7/EPg33N4TDMosYgAiIgAiIgAiIgAiLQNIG+BYDxxY8bcRwkv3DyHLn9Qmrru1zGOLo0vqr+hL7wY1MAmyF+Gzec7PzYObRzDEZoQ7L1tm+oXHU8vj36jA0Rf01C1h8j6jj+kH911NUxRm7cwB/L15bRZucHc4p5wYEyk9+HOtPmEPUcA3XUlcMvBlOtTtZnbQhmbUSiHzYjmaw+W8925Nw8RJnyftk/hxw2IhncZT/fPvoVSVU3QThf/jUQmnu7Znwfrbx/7fBa8+uhw15T/rVoddLP0GeHlYNOe27LaevWH0vseR57jBs201LZ8WLtYFw8wBXJjtU/R1to/L4Pab6yHrZx2ES70IWyTVwzWXPvt3G9QA91o2zrfb8p59dbXyjDOnuOch18oDu0LmzgE7ZskJRtrI8JANtXP6M/9KE/daGdAWDW+UFk+oCALtogRx/8MvXl2bH9fR0IRPtBa85FKIcurI3Y9QEd7IMy1inmFAfXrK/Lt2v7U19oXbBfSB42kOxnG+X9PLRWfJm6z32fqZ/1PiNed349+zFn/7RzfhZkfU6gL/SkMUcb/AFbm7L6WLkmy/74aYv1Pj9yhRxl2IesYvpADxKYQJ56sz4LQzbTfPBl0+YmccL7h4FeW23vx2yZMri/4hPBuG7tfR/Ps+73oIdyKFsfUB+6D6Nt28/XY/2ivJ/343q2PvhzyDbWl732/HVIvcihO3RN+jLQgcT1advbLvd7ntoe7zDa0xwO46xqTCIgAiIgAiIgAiIgAnUT6FsAGF8U8QXUJn4xtXXY/MAX8UFKGEeXxleHP/48cHyYQ7QhcUPBn1fbF/345b/I5pGd/zrGY/2wmxCoh19+smNAG+T8cfp9qpxXHSM3/+iDHS/KvKY4Z5wT5BgrDtZxvPacdWDHet8GZehDXbm/MUe9th5lPu3BjUVuHmITkJuK7Ivc39RL08c+0GcDw7487UHeb0M/tvtt9Jt2YvOqmyBV1xz9tOsA6wtrCYlrjddN1jXlB0ysTpSz1h3XI2z6/dhW9rOHY/TzPPawB184dvLgZ03Z8YIhdaSNNcQhix/1+WP0z609ttk6lKkL3G1b2txnrRfb335m57GjD/QRudXln6OtDj7QG1oXDML6QdG0evjDp24ZdGXAFm0oI6DK3/pFsJdBXAaQQwFgBmCpA/aLBIDz7Fi9/lizAsD4PLTXCeYPupBi14c/p1h/WHM4+BkAGcwz7IUSbFpZnKetC9+ef+6v0ZC90FoJydVZ54+RulmfxbsoO3KGTuqHPZR5jfqfE2hLY04dYIuDKasPZZrO6Ztvh/VZXCETYpXXB+zQDyywzpHADv2QoJeckwrzD/1iVZoP1MPrAvpoy9dBXcxxXwP/eN+DepzbezH8pzh7jnYEeCnr9+U55HjfhDprx5b9AHDafViePf9eMXHQ+6cf17N1IW0+bD3KXBNFrr20a5+6/WsyzS+7Pq1Mm+V+z1ObYx1WW5rDYZ1ZjUsEREAEREAEREAERKBOAn0LANsNGw7IfnlEGQe+IA5agt9dGl9d/mAuOC/cNMDcsB4bQfxCj/FT1s4h65jbzSluKuXNN/pW5Uv7yLmBBbvwx7ZZOxwn2u348/wt0w4b1jZ1oB6c0vhaOTsOlDkP1M12fyzg4duGrD8/qMPmGhNlbD3aaZdyVXO7oWd12XpuAqIOBzcRKc96tmEjEIdNaOMGI58yYT9sALJsc+qwfaHTnqPsb3Jm2bE+ZZWrboJg3vx5hz3Oa96ao2+U5zmvG/v54LehD9ch5P01Y3WiDIZMfhvO/QOyfl2Zzx7a9PMY9txgpR/83Ck7XsyH5QS9vEZtmWO3bWn8sj7/7Jg5hrQctvzxkjf1wHf259yjjfX+eqEs8lh2aeOBDvJogg/HGFoXaYHetHoGfTl+G8xFHYPBeDIXB/QgRxsCwXxiF0FX6qAcA7OsR079KFO3bWdwOc0Ox2H7h+xQjjmZ+XMGPTZlrY+0OUV/rJm0zzeOz65R1Pn60q4b6A/JUy/yvBRaK3l9qrb7PlOfrU/jDVk7vjx29u+Hvd6zPiegP4257yP8pE9pfTi+pnPrm7Vl69O4QiaNVVYfrlX051xAnmXkaONhrwXUsT8ZpvnA/syp39dhx80yg8CYHxwM2rIdOe6hQu2o430S5Ox51v0edSHnW1fYP+0+jO2+PasLMlmpH9ez9SdtPmx92WsPdjj/yENrAGsPh59sP/4d92XaPO/3PLU51mG1pTkc1pnVuERABERABERABERABOok0JcAcJ0DkC4REIGxBLDJYhM2ergZgza72WflUMamDDd0/Dadf0oAm4E2YbOQAWBb31ZZmyBh0v61EJaqVjve2Gd9hmS1VaM8eL1D64IBT+ULeq+pBoumU9f/roXWStNM2tKvz4R40l1g1QUf4ol1U3KYr+duEi/nleapHLcu9dIcdmk25IsIiIAIiIAIiIAIiEBXCSgA3NWZkV8iUIEANvBsig0AI/DLQLHtr/JYAgoAj2XSxRr/WmjCx/G2AZUVIMhqa4J9l3WG1oUCv6MDv+TR5DwOwt+10FppkkmbuvWZEE+7C6y64EM8sW5KDvP13E3i5bzSPJXj1qVemsMuzYZ8EQEREAEREAEREAER6CoBBYC7OjPySwQaIpC2uYcnpNLaGnJFamskoE2QGmEWVCX2BYGNE/HQumDAU/noQHBTS2JQ/q6F1kpTTNrWq/uKeOJdYNUFH+KJdVNymK/nbhIv55XmqRy3LvXSHHZpNuSLCIiACIiACIiACIhAVwkoANzVmZFfIiACIlCAgDZBCsCqWVTsawY6JOpC60KB39GBX/IYkikvPYzQWimtTB1FQAT6SkDXc1/xRxvXPEWj6qyg5rCzUyPHREAEREAEREAEREAEOkRAAeAOTYZcEQEREIGyBLQJUpZc9X5iX53hMGoIrQsGPJWPDgQP4/wXGVNorRTpL1kREIHuEND13J25yPJE85RFZzDaNIeDMU/yUgREQAREQAREQAREoL8EFADuL39ZFwEREIFaCGgTpBaMpZSIfSlsQ98ptC4U+B0d+CWPoV8MOQMMrZWcLmoWARHoKAFdzx2dGM8tzZMHZABPNYcDOGlyWQREQAREQAREQAREoHUCCgC3jlwGRUAERKB+AtoEqZ9prEaxjyU1vuRC64IBT+WjA8Hja2WMHW1orYyVUo0IiMAgEND1PAiz5JzmaTDmKctLzWEWHbWJgAiIgAiIgAiIgAiIwGUCmQHgK664wm3btm0Uq4kTJ7pQ/SihITspOl4wmzBhQkLBlocMy7gaDuYR64DzOq4Gr8EOBAFtgvRvmsS+f+y7bDm0LpoM/P5q4ZTk79SXvvzXrkk7Teju8jy24VtorbRhVzZEQATqJ6DruX6mTWjUPDVBtV2dmsN2ecuaCIiACIiACIiACIjAYBIoFABesWJFEgArGhAdTDSfel1mvA8//HCyEYu+4KY0mAQwdwr8DubcjTevtQnSvxkX+/6x77Ll0LpoInh66/T7BzbwSx5dnsc2fAutlTbsyoYIiED9BHQ918+0CY2apyaotqtTc9gub1kTAREQAREQAREQAREYTAKFAsDXXHONmzlzZrLR6D8ZPJjDj/O6TAA4TrOkuk6Aa77rfso/EdAmSP/WgNj3j32XLYfWBQOedeYT/vUb7oZJEwfuqV/LoMvz2IZvobXShl3ZEAERqJ+Aruf6mTahUfPUBNV2dWoO2+UtayIgAiIgAiIgAiIgAoNJIDoAjMAvgmFINiBqy7YNr8pFmz3Qzlfpot6+ThfnDC6jjCdomXBuA872PKQvzTb8R18ceJV1XgrpsX6k6bP+cUxp/axsmj76eeONNzr/YFso51hjbFgZ6LLntpzXRj/YBww5l2RBGeb+mHCeley82KerLT9rH3aZ+BQ7ZKGHifI4t22ot09zcyzsh7yI/9YOedi14Y/NnqMvDiS77lFnx2htQNae23JWm++b7QefeP3k+YF+OMDUT0W4gfvevXsTFevWrUvmhOeonDp1alIHubfeemvUOeo4b+jDc+TQxYRzq9Oe2zLk7bkt+77ZNvg4b968xJyt9/vQnzVr1jj/YFsoz9sEsXPozy/0ha4f1Of1s75wvm0fW/btWptcU7RpdVkdoT7gaeXpU976tNdeng3qDOV57EN9VDf8BELrwgY9i5T5emeucxvwRd1/3vGj3jWAstWNADH7IYcutNv6f/nhf4zqg9dIsw+eMLbnrIcOq8/aLFpOWw3Qz88NlHGtM9nr2/49Rzt9RM7rPPTZQVnK8O9b2b+9ab7S57Q8tFasrB0HbdBnyFl/eZ9jGaCMZJmhDrqYrA3U2XNbzmrzfbP9yBb90+aCvjBHfx4cb1pfayvLx7w2axs24TfXHcdHGeUiECJQ5HrOuy7stc1rATbTrgO/zV4Xedc/9UM3kpWHH2mJ/aytNP/+f/be7VmO67rTxL+iJz/4TREd3a0IR/TDGU2HR+Po6Ihuj9Vhzzgo8VA9nvDMqClSpmWTFGUcjBAeyd26kRLbGnLahzZHvLlFyexDWZRAiiYpiQIBAiAuBECCIAACgmReBIraEyurVtXKdTKzsrIqc+/M/CqiTu6d+7bWt1dmVebv7CxbR/qzeZteVKa2aJsmx+miedIx2KZLgDlMd26wDAIQgAAEIAABCEAgHQK1BWC9wBLTy9K+rCgvF2h6E0dupOhNf+nTX3BqPTue77OsP19P8vbl+7RlkhZb9IaP1tXHAfu6ktc6Pi322TIptzb7Mu27bL8VzbRu0VbYyTjyKuvL7rdp32aZMrXFtpG0vKzfWk+3df2SedGY0ba6tf3r+BJjGldST9rKPnnZMq0v5TrveuND89JG6mn7rJPpn7r26zjSTOy1+SrfbD1tq3aonXWOF9+Pzdu0t03LxEYddxk7pH3Rqy43mQMVZ1Xs1fz9998/E1b9GLadlElbFX1VDNZ+fF2bt2npx+Zt2tumZWKjjuvb+zbWBysA2/1F6UU3QXQOpa2fX91XFEOL2qkt0lb6lZdtY9NF42p7W8+mfX9av2y/xKj+Y4iMp/G6zHGyaAxbLulF7H198uMgUBQXywqjWl8EWBV9VQyWraat6CvHj9aV9tJWRV8p07T2LVu7X4RhLwhrXVvPt9M6TbZlESHj6We4P4bl+NZzlhzn+t2g7Fxkx5B+ta2m/eeb1NcybbvonFJmq7Yv2xbFiq1r7fDnURlTfbdtJG3bSX6R/crEt/X92LxNe9u0rIit2qp1NK/bpvOo7W2/Ni3lNm/T2raojuwT/ywjW580BJRA3eN5meOiLE5lTF9m49SWLXP8S7+2H3uOVT9l2+fjdNE8WT9Jp0mAOUxzXrAKAhCAAAQgAAEIQCAtArUEYCuKifn2YlLS/m1vjti6KqDa+nqzzNaTMexFsa2vaRmjqj9vp+Tl4lXby1ZFAimzL+lbyvUlafXJ2lXWn9YXblpH20ufZX1rXSmXd5l9IpoteklbvSGo9kibsjF0TLtVm+0+TZeVqc1ST+vomLKtei3yS/qTfstetsyOLzcw9GXTsk9skjmV+sJLmUlZ0Xi+jvYr20X2Sx21S/pRLjJO0Vi2b20n+4Sx5O3LxqWU6TxIHdtW0v4tY9t63jYtkzFE0NRXHTt0rKq5r8NNhVRZQWtXzKqIqzb5rbaT/bIy2Nov+6wwK2VSR1+2raT92wvH3jbpR9rIGI8//rh2m22176I2uYohZKuA/b6i/KKbIBoHRfMr/Um5vrSu7pcYKWunbSQepI5tY9NF7fUY0DjRuLXj2z4kXdZG+pd22scy8anj67FQNoaMX/RaxL6oDfuGT6AoLpqIo/obv7atPvZZBWBbJuKtFXAlvrVc0ioAi0issS9bGaeoP20rW9te87YPW3eZdFk0SN96XEod/azT49uOLWXykrKic1HZcS19+M83tceOr2NqmWzVHknbur7MtilKF8WKrad9+/OosJGyspe2k/I69ksdfdm2kvZvnRet522TfqSsiG3ZXOjYsm0yj1U21i1TBuqX2KL2ypYXBBYRqHM8L3tc2HiU8TUmNa41bqVM9ulL20m53S/lVecvra/9y1bq+5fUW/Z8a/uUtD2X1C1Tf217ZVL3OF00T95X8ukRYA7TmxMsggAEIAABCEAAAhBIj8BCAVguorxoZi+2bFrcq8rLxZrvS5H4dlUXpVq3qj9vi79JJnboxaPaoFtfV8eTcrXL17H9SX3hphfKtr23Wcuq+lO7ltnqjThpU2cMraNj2LxN2/58usxn2S99yHaVl2dk+yrjKnVEbJOx5S1p+xJOMndin2x1zqRO0XhS3/dh+1uUVg46jrItGsv2pfVkn/gqefvSuJR9Yp+U27f0Ly/bj89LmTDytmk94aM3eWTfIjvsWPb4kLbLvsQnEX5FTJWX5EWAXacALCKt9GvfXuRVu3V8taXINi2TFb766GfbvqyN1ll2u+gmSNX8Vh0/Ve2sjUXnHCkva+9j3saIjR3tQ+pXtVFb9FhYJj6XHUPH0u0i9lqP7bgIFMXFMqKo1m0iAOuKYH18s/Ylx5aIvF7olVXCTQVgFZRFdNZxdby627LI8OcCe3zLOaPoVXQuqjp3yBj+8037teMve05RW7Wvqm1RrNj6YkfR57P3y7aR9DL2y+ea1Ldv6d/34/Nltmk9z9bbbM/92WDTP03mUe3VsTVvOVSVFTGW+rJf/ZyaxwYCpQTqHM/LHhc2hquOobLvc8uev3w/Zc72+ThdNE9lPrM/HQLMYTpzgSUQgAAEIAABCEAAAukSWCgAywWnXATal70ItWmpUycvN1L8S9rJzSd56UVq3Rs3Rf1JP9YW6VOFLe3f+2VtkgtztUf70XZiV1V/Ul/aF9kvF8rar7Wxqj9rV520jCvj68vaX8ZA6/g2kq9bVnbjTNprP9p/062dF9tHGVepIzzEb3nrnMh+mQdpJy/1UfYpI9kvaT9fVXGTdVbxR8Ypi40y36x92rX0o3EvPqn9Wm63tsymfb9SVmabthNeykzbl9mhbaSe9LsKN5kDEVKLBFnZ71fYqv/STtvIPsmL8CovFY9tubbTulpW1I8tK7NN24kAbEVg2V/WxtqwTHrRTZCq+a06fqraqX1l5xwpL2tfdc6zsaN9yBhVbdQWe8xKP3Xic9kxdCzdLmKv9diOi0BRXNQVRH09iWV9rLOKtyq8ympgK7xKXRFzpQ8vykqZtJNyaSd1JG3biBhs+7O2aHvdZ/N+LK1TZ1sWGdK/nC/lJce/5PVzXNJ6fGv7snNR1blD+/Sfb9Knlmn/dkwZy5ZLusxWbV+2LYoVW1f6Lvt87tt3h6q5UJ9XmUftw8+Nxo2Ul5VJPOl3QF9H22n/bCFQRqDO8SzxaM85i44LG49VdRd9n9NzZtH5yx4j4puMqfWLfJX6cv7Rl9pYZZ/W8W0kX7dsXcfponlSG9mmS4A5THdusAwCEIAABCAAAQhAIB0CCwVguZD0L3uBZtNSb1FeLgqljr61f8lLWvfbC07ZZy9Kbb6svyJb5CJV2srNHUlL26qX2mK31o6y/qS+3gS0dkh9eduX1NU+y/qz9eukrb2a1nHLxrB2yBg2b9NFZTqGbJWptpGtspCt2lHHj7I6fjzp0/er42sfMucaa7JP6utNPsnb+hqH2lbq6pg2LrV8ma30ozz8uJrXsZSl7tc4kbyktZ5sbV0pty8p17Y2LXVsXtJlttl6lneVHdJG35a1ta1uWuyyIq/kVYCVPiSv77LHOEs9aaP1ZGvrelukXMewaR3PlpXZZtuJ4CtvbV/WxttRN7/oJkjZ/Nr51LHsfJe107qy1Xm2W+lXy4SDvmzfemz5c7Kto31oDBe10WNW2um40m5RfGqfdcZQ+4u2i9gXtWHf8AkUxUUdMbSojoq+eoypwKt1RbTVMhWKZZ+8tY5spY4Kx9pGhGBJ2z61L9n6/dpe+7N17VjLpMuiQfq2x7f9DJbPPTu2rWf36zmh6Nwh40pdPRdIHa3vyyS/6JxibbC2lvmn+4tiRctkKzaWnUe1XH223wesb1Kvyn47nvapXHw/Ni/pMttsPcu2bC7UBmnn3zovZW3tWMvab8dSftqfbNU/2aodaitbCHgCdY5nPbYknjSmymJb+td41LGK6tq+tJ5tV3X823ratugcq2WylTb+vcgXP47N27T2r5z8OOs4ThfNk/WVdJoEmMM05wWrIAABCEAAAhCAAATSIlApAHdpqr/o63LsRWOlbFuR7WKvfcnFs16Q2/1jSovApDcLxuQ3vo6HQMybIGM/58RkP54I75+nRXGxjCg6prpls7vs96+Y56JlbbU+F8WKLR9bOuY8jo01/q6fwFiO574fp2OZp/VHeDo9MofpzAWWQAACEIAABCAAAQikSwABuMbcrHJTr0b3a6/S9wvydQMR4XfsAvi6mdJfegRi3gQZ+zknJvv0IhGLlEBRXIxJ1F3GV2Xmt8t+/4p5LlrWVutrUazY8rGlY87j2Fjj7/oJjOV47vtxOpZ5Wn+Ep9Mjc5jOXGAJBCAAAQhAAAIQgEC6BBCAa8zNKjf1anRPlRYJyMpf5q9FwHSdDAFugsSbCtjHY5/yyEVxsYwoOqa6ZfPYp8/vVWwtipUyJuyHAATSJsDxnPb8qHXMk5Lo75Y57O/cYTkEIAABCEAAAhCAQHcEkhGAu3OZkSAAAQgMjwA3QeLNKezjsU95ZOIi5dlJyzZiJa35wBoIrEKA43kVet21ZZ66Y93WSMxhW2TpFwIQgAAEIAABCEBgSAQQgIc0m/gCAQiMlgA3QeJNPezjsU95ZOIi5dlJyzZiJa35wBoIrEKA43kVet21ZZ66Y93WSMxhW2TpFwIQgAAEIAABCEBgSAQQgIc0m/gCAQiMlgA3QeJNPezjsU95ZOIi5dlJyzZiJa35wBoIrEKA43kVet21ZZ66Y93WSMxhW2TpFwIQgAAEIAABCEBgSAQQgIc0m/gCAQiMlgA3QeJNPezjsU95ZOIi5dlJyzZiJa35wBoIrEKA43kVet21ZZ66Y93WSMxhW2TpFwIQgAAEIAABCEBgSAQQgIc0m/gCAQiMlgA3QeJNPezjsU95ZOIi5dlJyzZiJa35wBoIrLaD9ccAACAASURBVEKA43kVet21ZZ66Y93WSMxhW2TpFwIQgAAEIAABCEBgSAQQgIc0m/gCAQiMlgA3QeJNPezjsU95ZOIi5dlJyzZiJa35wBoIrEKA43kVet21ZZ66Y93WSMxhW2TpFwIQgAAEIAABCEBgSAQQgIc0m/gCAQiMlgA3QeJNPezjsU95ZOIi5dlJyzZiJa35wBoIrEKA43kVet21ZZ66Y93WSMxhW2TpFwIQgAAEIAABCEBgSAQQgIc0m/gCAQiMlgA3QeJNPezjsU95ZOIi5dlJyzZiJa35SMGaG2+8MTPjwIED4TOf+UwKJmFDTQIczzVBRa7GPEWegDUMzxyuASJdQAACEIAABCAAAQgMngACcI+n+Prrrw9F75deeqnHXmE6BCDQhMAqN0HkBrM/l8i+VF9t2Sr9Njl/rsK+DcaPPPJIbj7/03/6T4XDyH7x+Z577iksZ+dqBGLEhT+WmdvV5rCr1jFipSvfUh6n6JxftC+GD/Y83uRzKYbNjDkhEPt4lhi275jxY+2QtMS1vCQd+xV7nrz/fH57Iovzqc3hYoupAQEIQAACEIAABCAAge4JIAB3z3xtI8rFs7+oL9q3tgHpCAIQSJbAKjdB5IacFQnlPJK6AOzPfeuYmKbnz1XYr8Nu24eKBnafrB6z86t17D5bn/R6CMSOCzlGmsb0egjQS10CsWOlrp1Dq1d0fBTtG5rf+NMugdjHs41h+bzX1eTtel3cu7VFP5OkpuyP/Yo9T9Z//V5m95FeTCClOVxsLTUgAAEIQAACEIAABCDQnMBNN93UuDECcGN08Rvai2q1xu+TvL6toOP/y1jycoNALkDlJXl95JzvU+rZvrR/Kyb4NjZv03rBa8Wcov7UP9lquW61re1X62mZ5qVOmZ22fVla+9F+bT3ri4yh48gKLGUp7e1L2utb+5S6uk/7kDZ2LJ9fpsy2rWuntZl0mgRWuQkiMarHvsaHHuNdxqOSLYp/LVP79HjR/VWxLOcs6dMeh0Vj+ONI+160XYX9or6XLffnZ2kvrKxv9lxv+7dzrfNvyyVdxM3ut+PYtD0/an07h7auTdt21j6pI34U9ZXtTOBP7LiQOVRGgsPy858twtO+dW5kn86Bpi1a28bHjIwt5XrcSVr71T6K9kmZ3S9pXcls9xfV0/7VZs1LO30X2ePrq31dbWPHSld+pjaOjyexz+4rO2akno1vW0/a63EnaY0tTVsGsk/f9viRfRq72l7ztkzSRceGb2PHJN0+gdjHs40RiRvJ60vS+taYk/iVmNGXlGuZ7NdzppRrW/8ZInmNe+1H62vsSp/al/QT+xV7nqz/wk452f2SVuZ2q3Vlnx7vmtb29rzk56usL9uvnlvK+tFxYm5TmsOYHBgbAhCAAAQgAAEIQGDYBET81XcTTxGAm1BLpI1cvOmFmppk98kFm168ycWhvTCXvF4MShu5KJe6uk+22tb2KeNIP3pjQMaQvuQlabXHt7F5m5a+bL6sP/VPtra+2Kjj2/2+Xlm/tk2dtO/XtvG+SJnWzxLuj7ASu7SOstNqktc+iurYsW3a1/VlReW6T7a8+klglZsgErs2/iRm9BhXGl3FY9mxqnbIVuyzb7Vd9mm51pdzmZ7XdF/ZGNJe+9K6dbarsK/Tf906fo5sO3veFj+FiTLUc6jWl/1+/qWsjJuMW3QuszyLzo+Wta1r076d2OHts/XVhxS2seJCPheFibyLXj5OPD+bl7TOrcSJzIe+ZL9+T/BlRced7Vf7KNonZbrfxq3dX9Re20iZjxtbVtTW19c6XW1jxUpX/qU6jsRF0duem8R2f8wUxbfUk77suVPyTY4faac2+NjUsqpjw7dJlf9Q7Yp9PGuMCF85R0s8yKvsnC3nb/2epOdyPbfLftmn7W1aY1TG0/pZRfNHyuxbi2Rf7FfseVL/haPOke6zW2GlrGW/zUu67ByjfUhby9u2l3nTOdX9/txS1o/uj7lNZQ5jMmBsCEAAAhCAAAQgAIFhE1Dh126X9RgBeFliCdXXCzVrkt1n01LH5uWCTy/WZb/csLIXoHLxpxebWq7j2AtDKbNvvfFl92na9idpvakg5bZM68tW+9Ox1Q+tozcs/H4tX9Sv1LN1ytLan259vSJf5IJa6itn64OkpVzLrB3armgs3adba4fu021Rmd5gkDparuOpLd5O8v0g0PQmiMSB3jxSTyU+9NjT+KiKq6ZlRfGofelW7VDbZCtlGr92v9pqY7morvatWx2jqK7tvyzdlH1Zf033CxPxoeil522to4zEd++3ctGtsta8bpWbcNf+pMzWl3TR+VH7sNs67cQ3aaNja76onyIOXe6LHRfC07LS40NZed7KRsrXXebnqejY1/G1rpyXxGb7Utvt1ttaFm9aT/tTP4vqa52utrFjpSs/UxtHY8DaZffVPWa0vbT15yYbd7Zvm5b2Nq/potiUsrJjQ8YqaqP2se2GQOzjWWLEvtVrjSufl7iRMnlJ/EgM6/dCOVdrDNs+Ja2x7vvV/mVry3Qc3dp6MdKx50l9Fh76maj77NYylP02b9O+rOr8Je3kLfOtL8kXnVvK+tF2MbepzGFMBowNAQhAAAIQgAAEIDBcAl709fm6niMA1yWVYD1/0Scm2n027cv0BpHu14t4FQnshajc2Je+7Fvr+zEUk99v85KWi0m9ueDL9EaD9uW3tr74oRevdr/6pX35Mu3T7q+TLuq3zBe9YJZt0Uvs9hwlb9mX2VRkh/paVaYX9rbfRXYW2c6+9Ag0vQlizwXqlcSHxGKMeLSxqfb4bVmdolguqlu0T8Yo2+/H9/mm7H0/68iLD3pe0f7k3CD75WXTWq7nfc3bPuT8X3aO1fpF5zIpk35kTuqc66WunsOq2mm/1kfb1tqr9sXaphAXes5v+1jWebFzqGnlb+dJ7bL7tJ72JXGpsadlvr7NS7puvOkYZfV1vK62KcRKV76mNI6NH7VL9y1zzNi2ZecmqaN9+7TPL4rlsmMjlXhWHmPdxj6ebZzZOfD7bV6/B8hWXj4v+2z9qn6ryrRf6Sv2K/Y8Wf/L2EodX2bzNm3r1j1/yWesfs5KXzI/mpf+qvqx9sdKpzSHsRgwLgQgAAEIQAACEIDAMAmUib1l+6soIABX0Um8zF/0ibl2n9xg1VVZclNIL+p9PWmjN6zkos+2K0KgF+9SVlbX2lE0nvShN4dt3bL+rB22vr9w1T79mGX92r7qpH2/0qbMFynT+lnC/BE7xSZ96dj25p2kdb/Us2mfr1smY8pc2/qS1v6yBH96SaDJTRCJQ3teUMclJiROYsRj2bGqtsnWxq/fr+W6v6i/on3azp5DtI9F2ybsF/XZtFz/Yce2lzm2N/TEf5lbeen5wNbX+Zd99hxbxK3sXCZtpZ+q86Nlbee0qp32q59Zmte+rL1SFvMVOy6Eic7lKsdy2fcIGw/Svz2X2DKdAzvHUq6xp3On9WSrdX0/ul/r2ryk68abjlFWX/vvahs7VrryM7VxbPyobbqv6pjxcWnb+nNTk+OnTix7G6raqH1suyEQ+3jWGPbe2pjx52yJU1vu89KXLbd9l40ndWyZfibp1vYRIx17nqzPwtt+hkqZnjssQ9lv85LWenZOq85ftr39zqT77TxX9WPtj5VOaQ5jMWBcCEAAAhCAAAQgAIHhEhCxt+hVtr+oruxDAC4j04P9eqFmTfX7JK9vvckqF5hWDJByvWGlN2Q1b/vWtLTXcr2I1zG0juR1PNln85LWi1VfVtaf9qv1dTzZ6suOofXUhrJ+bT8+rW2r+pWyIl/sxbOUS96+/FiS1wt/2Upe5ki2de3Qet53O5baof0ustPaTDptAk1ugtjYKErLcd5lPArhsmPV0ve26jGmx6LmtY3W1/gvG0Pq2eNI2y/aNmG/qM9VyuWGnfosW+Vi+7Tlej7XclsmaX0VcfN1Ja/nMknbsSWvfG1a+rf5qnZa19os9e1b7Y29jREXwtuykFjQV9NjWT+LpF+dP+3TjlVWpsedrWv3+XbStx1L7NbvLHa/rydldeNN25bVV/+62saIla58S3kcH09iq91XdsxoPamrsaz7/LmpyfFTN5b9sZFKPKc8513YFvt4tjHs/ZUyfdtzr8St7Nf49XnpR+prW9nqS9K2L90vW1tf0tq/bW/rd5mOPU/eV//5reWer81LuuwcU3b+kjb2XTSOPbeU9aPtYm5Tm8OYLBgbAhCAAAQgAAEIQAACZQQQgMvIjHS/XHzKhR6vdgnIhbd/wd0TId82AYnDqpt2eqOubTvov78EOJf1d+7qWF51jqjTnjoQGDMBjp8xzz6+Q6B9Apxj2mfMCBCAAAQgAAEIQAACEOg7AQTgvs/gGu2XVQxyIYnos0aoJV0JZ/9CAPZEyLdNoOrGEeeCtukPo3/OZcOYxzIvqs4RZW3YDwEITAhw/BAJEIBAmwQ4x7RJl74hAAEIQAACEIAABCAwDAIIwMOYR7yAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgwG8AEwMQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEhkJgz6FDhwJvGBADxAAxQAwQA8QAMUAMEAPEADFADBADxAAxQAwQA8QAMUAMEAPEADFADBADxAAx0P8Y4BHQQ5Hy8QMCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEBg9AQTg0YcAACAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgaEQQAAeykziBwQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgMHoCCMCjDwEAQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACQyGAADyUmcQPCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEBg9AQQgEcfAgCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAASGQgABeCgziR8QgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMDoCSAAjz4EAAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCAyFAALwUGYSPyAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgdETQAAefQgAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQGAqBQgH4ySefDLz7wyBWMBIj/YkRO1c2Xux+0v2cT+aNeSMGiAFigBggBogBYoAYIAaIAWKAGCAGiAFigBggBogBYoAYIAbGGwNW99F0qQCsFdimTUAO6FivmGPH8rnv4/o58/m++4f9EIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQGAsBMp0HgTgnkdA2cR24VbMsbvwL5Ux3nvvvXDw4MHwjW98Izz44IPhwIED4e23325knp8zn2/UKY0gAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQ6J1Cm8yAAdz4V6x2wbGLXO0pxbzHHLrZoeHuvXbsW7r///vDHf/zH4YknngiPPPJIuOmmm8Lf/u3fNnLWz5nPN+qURhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAp0TKNN5EIA7n4r1Dlg2sesdpbi3mGMXWzS8vTs7O5ng+/Wvfz389Kc/DXfeeWeW379/f5CVwcu+/Jz5/LL9UR8CEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQCAOgTKdBwE4znysbdSyiV3bABUd1R37F7/4RXjxxRfD008/HY4fPx7eeuut8Ktf/aqi53mR1BOhs279ect2Uz/72c8yQbbNUV577bVs5a+s+H3qqaeyxz4/+uij4bOf/Wz4zne+E4Trslz8nPl8m/7QNwQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwPoIlOk8CMDrYxylp7KJ7cKYumNfvHgxSF19P/PMM+HcuXNBHm9c9hJhU8ovXLgQRAgVsTOF1y9/+cvw6quvhp/85CfZtk2b5Dd/Rfy9+eabw7Fjx7KhhInwEBG9il+ZXX7OfL6sHfshAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAATSIlCm8yAApzVPS1tTNrFLd9SgQd2x//Ef/zE8//zzMwFY2sn7yJEjmZDphxaxV0TOF154Ifz4xz8OZ8+eTUYAPnXqVBAB+9lnnw2vv/66N32t+a2trdnjni9dupTru8njn6UDP2c+nxuEDAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQLIEynQeBOBkp6yeYWUTW6f1I488EuTd9LXM2O+88072+Gd5DLS007espJXHKcvr3XffDSJ0ilgsjzyWVa/SLoWXrLg9evRoJv6KACxvWdm87teJEyeycZ544olwyy23ZALw5z//+fDcc89lj9GW1cfLPvbZ2ujnzOdtXdIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAALpEijTeRoIwGfC9uZG2Niw761wwPl+Znszq7O5fWZecmDLtdM+drefNyJVRaBsYqvaaFmXArCMKcKlrJqVVb1it75/+MMfZvtF/JR9srr2/PnzamYSW/kNYxV+ZSv5n/70p2u1TVZKf+ELX8h+4/f222/PxF95BPRtt90W9u/fH2TfY489lnFsKgL7ePH5tTpEZxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAq0RKNN5GgvAVtg9sLURNrZUAj4QtjY2wub2gUwotvWKvMu3Laoxnn2f/rOtUPYuo1A2sWX117m/6dhvv/12ELFXhFTpw74PHz4cRAhN6SWCtBV/RcBuY/WvrIB+4403wpUrV8K99947E4C/9a1vZeOJeP7mm2+uhMbPmc+v1DmNIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEOiNQpvOsRQAOsrJ3czuYtb4hhMlK4UoB+Mx22NzYDHaRcGdEEh2oSACuMrVsYqvarKts1bHlkcrSh75/8IMfzB4HvS4by/qR3xle9Hjpn//859lKXyv+yiOrRfxtugK3zB6//+tf/3omAP/RH/1RtmJays+cOZMJ57L6WG0XWyQvj6iu8/Jz5vN1+qAOBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDAegnIU2H1XdSzlslWX2U6zxoE4OkjoWcrgHXIxQIwq3+VVX5rReB8ye5c2cTurrl7T9ePgFYLfvnLX4ZXXnklyKOfxX77lhXAKm5q/XVvZZXt6dOnw6lTpyrHeuGFF3Irf0Vold8obvslv4ksv/srB/C+ffsy4fe9997LhF55RLTsl99JPnfuXPjMZz6T5Q8c0BX41db5ePH56taUQgACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEItEHACryyQFB/ivTatWvhi1/84kwcblUAtr8BXLzKd5EAPHlU9C7duA1iPexTROA6r1UEvBgCsKy8PX78+Ez0ldW1Z8+eDSL8qhD80ksvBRE823rZFb2SFsHVvkSgFhtsvR/96EeZ4GrrtZV++eWXw6233podyP/xP/7HICuRdcXxt7/97Wz/V7/61fDAAw+E+++/P/zn//yfM6Zi96KXjxefX9SecghAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgfUTsAKwpmWUW265JSf+tioAz0RfefzzxlbYvf6wWgA+s71Z8Njo9cMaeo8xBbxlxxbxV1bRSjt5i8CqK2pl1a8te+2111qbOivsSlrGFZFVXiKiyspgW0fEabGzjsC6DqNl5bEe2CLuihiugrgI0TfffHNW/tBDD2XDyW8qC9s69vk58/l12E8fEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACyxNQfahqa3st03nW9gjomSA8G7VKAGb17wzTiomyiV2x21rNlxn73XffDUeOHJmJv//wD/+Q/ZauHUhEYK0j5W+++aYtXlvairuaPnToUBAhVVYj6z7Zyn55ZHSXryeeeGImAH/rW9/KCbvy6OxPf/rTWfk3vvGNzCxZHawrhBfZ6efM5xe1pxwCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQKAdArIgcGtra6YTeSFYHgdtX2U6zxoE4BBC4SrgcgE4W/1buGrYmky6DoGyia3TtqtHQEuwnjhxYib+Pv300+H1118vFC1lJevRo0ezurIyt86q1jq+2jrSp4xhhV5Jy28S675nn302q3PlyhXbtPW02PZXf/VX2YH9yU9+Mjz33HOz1b8yuKyMvu2227Ly7373u0vb4+PF55fukAYQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAJrJSA/EWrFX/np0KJXmc6zHgE42BW9k7T9jWBJz1cIT8rn+SJz2VeXQNnE1mnflQAsK2ifeuqpTNT9wQ9+kP2WbtWKVfnvBV0JfP78+TquLF1HhOaTJ0/OBF8Vfu323LlzS/e7agNZhawHtRzMIpSLrVevXs1WKIvoq78PrAKw/gh4nbF9vPh8nT6oAwEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQg0C4BWSioInDZSGU6TwMBuGwI9scgUDaxXdhSd+yDBw/OVv+K6Kq/Z1tlo4jA8lu4Isi29ShoGV9+31dW2VrhV9LPP/98eOutt6pMbKVMhN4//dM/zQ7ov/zLv8xWQH//+98P+/fvD1/60pfCzs5OEOFXDvivfvWr4Xvf+14QvlWCujXUz5nP27qkIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAE4hEQPajqVabzIABXUetBWdnEdmF63bF/8pOfZAKwiK3+2eRVdspqWBFijx07tlS7qj6Lyi5cuJATgOVR0Musqi3qs+m+U6dOzf6bQ34HWV4i8soB/hd/8RdBbP3Zz34W9u3blz0K+u///u+zFcJ1H5Xt58znm9pNOwhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgW4JlOk8CMDdzsPaRyub2LUPVNBh3bEvXrwY5Pd8L1++XNBL9S5t2/ZqXBlHhGYRnGWVclcvEXDvvvvu2ZiPPfZYJvZ+/vOfz8ReEXblLY/Rlt8jlsdBy+vnP/95Vi5cpJwVwF3NGONAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgTQIlGl1CMBpzE9jK8omtnGHSzSMOfYSZtaqKiLqK6+8kv32cJerf2+77bZM8H3wwQczIfezn/1suPnmm8OBAwfCu+++m3tctjw62z8+W/J1xV8B4efM52vBohIEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgEB0AmU6DwJw9KlZzYCyiV2t13qtY45dz8L0a8mjnG+55ZZw/Pjx7Pd95VHPf/M3f5M95llE6XW//Jz5/LrHoz8IQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAIF2CJTpPAjA7fDurNeyie3CgJhjd+FfF2OcOHEifPnLXw5f/OIXw5133hl+8IMfhKtXr2a/eexX+67DHj9nPr+OMegDAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCECgfQJlOg8CcPvsWx2hbGJbHXTaecyxu/CvqzHkUc9vvvlmeOeddzLh1z/6eZ12+Dnz+XWORV8QgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAALtESjTeUoFYGnAux8M2gub6p6Jj37Eh58nO6u+jHw/55R5Y96IAWKAGCAGiAFigBggBogBYoAYIAaIAWKAGCAGiAFigBggBoiBccaA1X00XSgAayFbCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhDoDwEE4P7MFZZCAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQqCSAAFyJh0IIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAAC/SGAANyfucJSCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAApUEEIAr8VAIAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAoD8EEID7M1dYCgEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQKCSAAJwJR4KIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCPSHAAJwf+YKSyEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhUEkAArsRDIQQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAIH+EEAA7s9cYSkEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBSgKdCMBXrlypNGLohfjP/A89xqv8I/6J/6r4GHoZ8U/8Dz3Gq/wj/on/qvgYehnxT/wPPcar/Bt7/D///PPh9OnTo32L/2N+jT3+8Z/PP47/8RIY+/E/3pnHcwhAIGUCnQjAly9fTplB67bhP/PfepAlPADxT/wnHJ6tm0b8E/+tB1nCAxD/xH/C4dm6acQ/8d96kCU8wNjj/0c/+tFoxV8RvsX/Mb/GHv/4z+cfx/94CYz9+B/vzOM5BCCQMoFOBOBLly6lzKB12/Cf+W89yBIegPgn/hMOz9ZNI/6J/9aDLOEBiH/iP+HwbN004p/4bz3IEh5g5QdkXwAAIABJREFU7PH/3HPPjVoAFv/H/Bp7/OM/n38c/+Ml0Ifj/2/+5m9C07ed2RdeeMFmSUMAAhBIlkAnAvDFixeTBdCFYfjP/HcRZ6mOQfwT/6nGZhd2Ef/EfxdxluoYxD/xn2psdmEX8U/8dxFnqY4x9vh/5plnRi0Ai/9jfo09/vGfzz+O//ES6MPxL+Jvk5dvhwDchCJtIACBGARaEYB//vOf53x5/fXXc/mxZfCf+R9bzFt/iX/i38bD2NLEP/E/tpi3/hL/xL+Nh7GliX/if2wxb/0de/w//fTTEQTgh8LHPv7B8D73/tjj3f8Wsfg/5tfY4x//+fzj+B8vgT4c/17IrTtbvh0CcF1y1IMABGITWLsALOLvqVOncn6dP38+l+86c2BrI2xsHeh62Nl4cfw/ELY2NsLG7L0Zts/MTOo0Ecd/dfFM2N60HLZC15HQvf9+7sX/sc1/Ogy6n3+N/d0MNiOcBOL5H0J27p+dAzfCxuZ26Po02L3/Mu9Fx3vZfo2Xdrbd+2/9EJ+7P+dbC+L6L5bEmXdlEMf/Ap8PbEX5HIzjf/x5jzP/Mu8Lvu93HAfdz/+UQeFnXcFxoRPV0rZ7/9WRKYfZ53/RZ6LWbW8bx/80fBeqcfwPIZzZDpuzuY93DfTUU08lIwC/7+PXhX0/6lYEFv+jvPz8R7oH1H38+3se5v5H4WdCu7PTvf9ln3Fl+4fm/+S6tzDc5btPYUF7DLqcf7ne9/c4zmxv7r7u75BDl/7PZrHwO+70vDDg+Vf/i+IgCJOS858XcrWfRVvfDgF4ETHKIQCBVAisVQBW8dcLwOfOnYvnr1wEbG6Frc14N4Hj+O++7FZ8+LU9OXH8F68mN0FyXwjPbIftjhXg7v13c5+hkJvfG6Hj735ZaHXvv859nBt+mdPmTxz/02EQx/+CY1/OCFvdfw5073/B8Z/FY9l+E6wtJLv33zohPnc/59aCuP6LJXHmXRnE8d/5nN0QiRMHcfyPP+9x5n8y75ubZZ/9chNsM5SXq9Xr23Y//8JgctM/9903c8kdF+tzs7Sn7v2fi3+577tTQSi3r9Tq9RVE8d+d8wtvgq/PxcqeovhfdAM80vwfOHAgogD8J+GvTovgO18R3PUqYPG/81c21/nPgDPb253/87f4HSX+Z8C7P9/Php4muve/zOey/d7i9ea79z+70C0UekUYG/Tn3677nPp9L//dv1AgXO+0z3qLMv/ZV6DNXAzE+g4Qxf/s/G/nfCJ+l8W+F3Jnk7cg4dshAC8ARjEEIJAMgbUJwFb89QLwq6++Gs1h+dCTmyC6jWFIHP/dl135QCz576e2mcTxf/JfkLtvgLXt7e7+u/ffzb2atOvLsRa0u+3ef/GnhEG7rhb2Hsf/dBjE8L/LC7zCSTc7u/e/LPbL9htjW0h27791Qny2F4K2rJt0XP/FxzjzrnTj+G98jij+CoM4/sef9zjzP5n3ra38zS+1ZXIdsF3yhASttd5t9/OvsS9bf8NXy9brY1Vv3ftf8d0/wnfgGP7vPud3P+8aE937X+FrhPn/3ve+l5AA3P0KYPG/81fE+x3e1+7j31pQcSzYai2mu/e/zOey/S06H+37n/jqr3uK9rXru/Te7fx7Hw+Erc3tsJ0TvruNg279t/Np/bRpW6f9dCz/c/eAFnweeCHXUrnppptsNpf27RCAc3jIQAACCRNYiwDsxV8vAJ89ezYSgsl/f2VPPV3wAdCmgXH8z3/gxxTA4/nvvwC3OcvlfXfvf37u55aV7Z/XaCPVvf/iRRxfi/jF8T8dBt37n87cyyyk438cLt37b49C8Tnu50Bc/+OfB+L4P431A/IY0LHOf5zj3R593Z//1GfdWmt0n25tWXvp7uPf+Lfrnx9MWXsu53qO6n/OEsmI/92eD7r3X/20KyC7n3dF37n/lSJv9xy++93vRhSA3e8Af+Whzm0R/7t/TVZ8lT3ys0t7Oo//nHPdx3tueK5/Ilz/TWYgJ4DJrgNbux6P7OeqjXy38e9WeqrPuhUHO74X3K3/bgann4UigMdaDBPNf5nn6Xc9ORbKVv8KMS/kKkURf/Wt++zWt0MAtnRIQwACKRNYWQAuEn+9AHzmTNe/ujhFnvugN2JwxzMSx3/54h/3t18UcxT/zYe/2hFr273/ZRd9ZfvbJdO9/+KPi//sWOj2xp9SjeN/MYOqL8Fq77q3nfu/69if3gzKYsDeFF23p8X9de5/YezrZ8EY/LfzIOeBOMe9WtH9/OvIuo1z3tfR4/g/P//HuvER138ZPe68x/F/7rP806P9vbt5fl5HbWxz23385/3L/J49/Sdf1qbf2nfn/u/6/FdLZDsC/zN3837mY8DyaD/d+fxXCsDd3wf4zne+07noah/5/L6PT0XgCOLv6dOng/gf65XFvXzvn53/urek8/jPuZg/D+SKOsp073+Zz2X72wXRvf9Tf3Lnwe7Pe0q1a//lmNfv/DPhz9wLzs4JHd4I6dp/5a5bYTDW81/2TxBbWwuffumFXGGnwq/dKlPd+nYIwEqGLQQgkDqBlQTgMvHXC8ByERDjZb8IyPg+35VNcfx3X3bly2CkG+Hx/I9741/jq3v/3dyrIdnNr+6ZdO+/OFzGYAajs0Qc/9Nh0L3/MvdFcR4nJuL4XyT0jsV/e2iXxYKt0266+/n3/sSZd7Uijv/qs2yr//tb7WxrG8d/8UYZtOVZvX679d/6XCddz4dVanXrv1hq/Zb85B+gJjdFfdkqntVrG99/a6f4X/TdwNZZb7p7/8V+8VP/6Uu23fpsCXbuf074sJYol6LvRr7e+vI7OzsRBWD5DeAfhH1/NhGB//v7f9C5LeJ/7Fcm+kQ6BjqP/xzs7s/3ueFDyOLN72s3X+Zz2f52rYk3/0b0NQJou97u7r1z/2e+iv/6uTdnMROFd5vayp7O/bdeyGfh1oGQCaHZozBtYTfpqP5n/wy4+PrPC7lW9PVpS823QwC2dEhDAAIpE2gsAFeJv14A9vlugPgLYL0Y1i8E3Vgho8Tz317oxvnyG8//yU2vDv/RrzSgup//4rnu+j8fFUj3/svIxQzUpi63cfxPh0H3/k+Off0v4Plcx4mJ7v0v87Ns/5xQG6nu/bdeiM/df+ZbC+L6L5bEZRDHfxPrNW8C2DlbZzqO/zrv9jvgOr2q31e3/pt5n/7Tp9wAy3/3ydep70mzmt36LzYW+af7dNvMlyatuve/7PNf0Gx1vhqme//LYqDJ7K3epnv/K2I8wvw/9thjnYuu8xXAIgCfDqcf/5MwWQk8zcu+jt7if/xXvPsB3ce/pV1xLNhqLaa7979krrPvgd1fC3Tv/3wyddGLbucl3aW691/mfzNsy8+/mBuAE+FXjoduY6B7/3Vu7bFv01rezTae/+JfPb+9kFuXjG+HAFyXHPUgAIHYBBoJwIvEX3/CP3nyZPd+Fl7olXwxbNm6KP77Dz7h0fEXH8Uax//pzR6/+ufMdtg+oJZ1s+3e/91ferIboBtxbgZ377/M624G3cz27lHi+J8Ogyj+F4o+cWKie//L/Czbvztm17mne/+t9eJztxf8dnRJx/V/8uSTmI8Ai+O/i/XsfDCmzz+JPMfAB2ZH+W7n3/ssefnnTzv3vk67ILr1v2Les2sAz6Jd36X37v2f/s6f/+6f+W/joH3fo/mfyLEfy//C653C74Ttx8C3v/3tzsTWuaj7UPhY9uhnFXzjrQIW/zt/2d/8zAbv9pxv/Y1y/psZEM9vNSGG/5PjP/+9XwRA+5MQal/b2xj+z3ySc97mVtgSQTTSL/HF8D9b8bo5fxR0xiO7J7y58HHAM3ZrSsTwP//Ul4kj2TER4VH4cfzXyat3/vNCrrZetPXtEIAXEaMcAhBIhcDSAnAd8dcLwMePH+/c37JHXmQfgua/wrowLIb/k5t/uuq5+5s+lmsc/6cWTC/6N/RxaBG+AHXvv3zpsXMf9zdAuvdf5r6Agb8haIO0xXQc/5VBvAs/RRrX//xxsHtVsFrZ3rZ7/8suesr2t+e79Ny9/9Yf8Tl/I8iWdpGO5f/kJpjE/xj9L4j1qQDW9Tkg1vwXfQZ27Xv3x//ued/9nX93nTbPA93Pf7l/2U3wnBjepueTvrv3f+qT/+4f6TwYx//yGGh/xvMjxPF//g/As2s/uSaKcP336KOPJiAA21XA14V9P+puBbD43/1r8s/+du47vu0zczla/GcWxD8PxPJ/8llnrv8iBUAs/ycBOD0OIvkuNkTxv/CfveRY2Jj9PvDsAG05EcP/LPZ3fdbFiYUY/s+ntN75zwu58/bVKd8OAbiaF6UQgEA6BJYSgOuKv14Afumll9LxOIIl+M/8Rwi7ZIYk/on/ZIIxgiHEP/EfIeySGZL4J/6TCcYIhhD/xH+EsEtmyJTifyYK7bo53h6u//pf/2sEAbg7gXe+6rh4TPF/zK+U4j/GPOA/n38x4i6VMYn/9OPfC7l1Y8e3QwCuS456EIBAbAK1BeBlxF8vAB89ejS2n1HHx3/mP2oARh6c+Cf+I4dg1OGJf+I/agBGHpz4J/4jh2DU4Yl/4j9qAEYefOzx/8gjj4xaABb/x/wae/zjP59/HP/jJdCH498LuXVny7dDAK5LjnoQgEBsArUF4FUMPXLkyCrNe98W/5n/3gfxCg4Q/8T/CuHT+6bEP/Hf+yBewQHin/hfIXx635T4J/57H8QrODD2+H/ooYdGLQCL/2N+jT3+8Z/PP47/8RLow/EvQm7Tt51ZBGBLgzQEIJAygU4E4MOHD6fMoHXb8J/5bz3IEh6A+Cf+Ew7P1k0j/on/1oMs4QGIf+I/4fBs3TTin/hvPcgSHmDs8f/AAw+MWgAW/8f8Gnv84z+ffxz/4yXQh+O/qfjLCuDxxjWeQ6DvBDoRgA8dOtR3TivZj//M/0oB1PPGxD/x3/MQXsl84p/4XymAet6Y+Cf+ex7CK5lP/BP/KwVQzxuPPf7f9/EPhrG/ex7CK5k/9vjHfz7/VjqAet6Y+E8//r2QWzfkfDtWANclRz0IQKAugZtuuqm0alVZaaNpwZ6rV6+GK1euhMuXL4c33ngjXLp0KVy8eDFcuHAhnD9/Prz22mvh3Llz4dVXXw2vvPJKOHv2bPbfrC+//HKQ3/o9efJkOHHiRDh+/Hg4duxYkOf9yyMfXnzxxSD/+SMffqv8dw1tmz+aAnawIwaIAWKAGCAGiAFigBggBogBYoAYIAa6i4Gxi7/iP/HWXbzBGtbEADFADFTHgBVHhFWTl2+3mgB8Jpw8uC98aL/9h7Ebwo2PnWliGm0gAIEBEBCBV9/eHd3fVATuZAWwnCT/3V2HeI+UwV1PnPNxO6q8+E/8j/f4H3v8r/aluP+nCvx/of+TuIIHzD/zv0L49L4p8U/89z6IV3CA+Cf+Vwif3jcl/on/3gfxCg4Q/8T/CuHT+6Ypxr8Xbn2+LnTfbiVfX98OH9ovgu+T4eTrZyZvEYTlCSL3PlnXJOpBAAIDI1Ak9BbtW9ZtBOAFoux/uf+RsOq7z+Lfqr5L+7ELYH0WgNcx/8T/uP8BYqUvxct+oiVYH/+5AZBgWHZmEvFP/HcWbAkORPwT/wmGZWcmEf/Ef2fBluBAxD/xn2BYdmYS8U/8dxZsNQfywq3P1+wme7KFrdtKrB/cF9738RvCV163I5GGAARSJ2BF2rJ0XR9WbV80DgJwDQH4VyGEpm8R0PougDX1XdohAIdMAO9rDMj8rTr/ffVd7F6H/2P/B4hWvhQXfZolug//uQBONDQ7MYv4J/47CbREByH+if9EQ7MTs4h/4r+TQEt0EOKf+E80NDsxi/gn/jsJtCUG8YKvz9ftyrdrJ9afDDd+/IPhxoN1raIeBCCQCoEy4Vb2L/vyfS3b3tdHAK4jAP/qV+FXDd+DEIAb+i7MEIAHIACvOP+9F4BX9B8BmAsg/8E7pnw7F0X9IYj/HP/9idb1W0r8E//rj6r+9Ej8E//9idb1W0r8E//rj6r+9Ej8E//9idb1W5pi/Hvh1ufrUvDtWvFVHg1dsAL45OtPhq/ce8PkEdHymOiPfzB86N7tcNIbn60gtr8rvDudE5ez+vvCTgi7fpO4sP/peLt+v1gfZ+3t0fzrT4Yb99+Q2S22yyrnD9nfOzZ2aJPd2zPhK/triuOF/Z0JO/fK2BN/s/4L6+nIBWJ8Vf1s7px9030Tn3UuzArvZftT09gmS8ALt03EX3HO97Oqw3tW7aBOezlJ9lUEEgHzvfd+1fg9BAF4Vf/HLoD1/RHQq85/X499XQG8qv9jj/9WvhTX+eBJpA7+cwMgkVCMYgbxT/xHCbxEBiX+if9EQjGKGcQ/8R8l8BIZlPgn/hMJxShmEP/Ef5TAqxjUC7c+X9E0V+TbtRHrJx+7Ibxvvxd2RYi8IRN8d/T3gjNB9YO766qgOKs3/X3hLF8uaH4lG3df2NW/FUunNHbuFSH3hnDjQdP3QRGuC+yRNplNIlib3zsW+x8zv3WsdueI+8xqAvAu8XdmmxGEc0OW8xLBPP+a1BWhNyewq6BvWb1+Zt601O+S/uYtSSVMwIq3Tcy07W26SV/aZo8m2tz2XQD+5S/fC03fQxCAm/ou7VgB3P8VwKvOf98F4FX9RwDmAqjNz9fU+27joih1n619+M/xb+NhbGnin/gfW8xbf4l/4t/Gw9jSxD/xP7aYt/4S/8S/jYexpVOMfy/c+nzdOfLt1uvrmbAjImzB6l+x72TRbwIXrTgtFRSllzJB84PhfSLO7gIxqb97pa5ZwZprU1C/yMZcm2mm0m5t0FwAzoT1IraV45bx2i0YZ+Ly/n3hRr9CWQXgovkTt0rGL+1PUbBNnoAIt01eRYJv0b5l+96zXIMDYWtjI2xum/9WqNFB3wXgd999LzR9D0EAbuq7tEMA7r8AvOr8910AXtV/BGAuAGt8TA62ynovivqHCf85/vsXteuzmPgn/tcXTf3rifgn/vsXteuzmPgn/tcXTf3rifgn/vsXteuzOMX498Ktz9f13rdb3deJoDl7PPD+feErB5fRWybtdwu0uwXKiY9lgmaZoBtCfkXy1N57zcpdBy9f37d3lW22RAi1VUJoJgCXir/SeeW4Zbwc36wPYVhgXxMBuKq/PBByAyNQJfRWldXBsKdOJalzZnszbGxshe3tzdEJwNfe/WVo+h6CANzUd2mHANx/AXjV+e+7ALyq/wjAXADW/ZwdYr3VL4r6TQX/Of77HcGrWU/8E/+rRVC/WxP/xH+/I3g164l/4n+1COp3a+Kf+O93BK9mfYrx74Vbn6/rsW+3Fl/to5oPbmcrSHc/Anpq4etPhp3HtsON9+4LH9o//z3g1QVgJ2haIDmBtEAQtXUlnatfIFD7+prP2ulv5M632WOjtU4TATjrt1zgzts7G2iaKPA3559Us3XWIQAv6M+bSH5wBEToLXtVlZW10f17NFF3K0LwyiuA778QzumAVy6EL/zonRDCO+Gh+w9Nfit41fK7pv2sYSsC5jvX3s29b//MVtD3n952R/ijP/7T8PFP3Bz+tz/8P3L1pF1eAH4pPHRFHDe+7lzNSJz70Ut5369cDc+2UvdC+OQSXNbh/9gFMPE/J4JO51wPgdncy7xUlS0xb7nxVmi3jvn3tnzhlHoeQjh1dsZm2f2+3zby6/B/7PG/li/FJmT6lsR/bgD0LWbXaS/xT/yvM5761hfxT/z3LWbXaS/xT/yvM5761hfxT/z3LWbXaS/xT/yvM57W0ZcXbn2+7hi+XTuxXiSaTvbJ46E/dO++8JXHngw72W/KPhm+sv+DIXUBOPebuGWwVVh1gnj2u8KzFccFAmtlfzeED+2fPN66rNpEAJ4LzrPV2PJ7xtN3zn61c9ph9qjmKvuWXAG8sL9SRyiAQDWBCALw2fCs2HRlKkTOBC8VRVctX5/4K4KSCEBv/+LdXe8/vf0zOeH3+hv+/a460k7aW2Hqk5nYHcKzOxM7Ne95iCioZeuua+1ZlF6H/2MXwHICsPxzg8b+XfoPAVfDF0SkrSpbQcRdNMdV5euY/1z/7h8ePvmjq5N//Fh2f0c81uH/2OO/nS/F1R9sKZXiPxfAKcVj17YQ/8R/1zGX0njEP/GfUjx2bQvxT/x3HXMpjUf8E/8pxWPXthD/xH/XMbdoPC/c+vyi9lru27UV6/4xypPfg90u+I3eArHYCZRq+2RrV5dOSyrr+xW9Be3zA6y4ArhgJXLOvmUF4H1hZ/obxDmR3Nqs/VvheZYu8Ffry+8yZ7/ZbG0usG8JAbhWf9Z20hBYgsCeJepmVVdeAeyEnn83E8GmAvCq5WsWhkQAeuvta4Xv//M/fCJ8dPNj4X/+X64rLJd20j4ngOnq5mzl40QAfPaUrAKeiIAT0XfKoq26SzBah/9jF8ByArBjP1n1qv/8kP/nhaqyXEy5PtdZto75z9kzPb5n//Cgti+7X9u1vF2H/2OP/7a+FC/72RWrPv5zAVwVe/pfpWzn/2ELC1gQA8QAMUAMEAPEADEwrBio+j48tDKu/7j+G1pML+NPivHvhVufr+ufb9eWr3kBuEBUnBk8EShz4qYRKGfVZokyQbP8EclFK1Jz4836niTytoeQb+8q22yZ3bn9VSxsZ064PrgvyEriQrtz/bs+co93npZp/amwnFsdXPSI6roCcN3+vInkIVCTwJ6a9WbVVhWAdVXr/LG3ugpyIoKtWp4Tm9YgDokA9OZb10rf/9Pv/LvSMmkn7fM2Tf3NVoHKaud3wkM78kjsif+Z6OdXiK69bl5ozNuXL1uH/2MXwLwAnHvUcXZkzQXgqrKqeWqrbB3z723L+zhd/XzXobDsft9vG/l1+D/2+G/rS/HsQynxBP5zA6AqROXmJi8IQAACEIAABCAAAQgMlcDYvu9y/cf131CP5Tp+pRj/Xrj1+Tp+SR3frh1fvag7ET2LxMvJilEnbKpAWehUmQBc8pjkAlFyMmaZYFzWf1l9Y2SJ3ZPxdJVtQwFYhsn6/2DIC7a6X/s39mTJcn+KHy1dYF8tAbjsUdUF/XkTyUOgJoHOBWD9jdMyAXjl8jWIvlZIEgHo52/+ovFb2tv+JD1b5ZsJvyKATUThcz+6MHk8tvld1LbqepvK8uvwf+wCmBWA9R8c9LHeE9Ez/88PRWVl89P2/nXMf5mNymJ+Lsg/Fr3u/rL+17F/Hf6PPf7b+VJc8xMugWr4zw2AqjAc2w2xKhaUQQACEIAABCAAAQgMj8DYvu9y/cf13/CO4voepRj/Xrj1+bre+XbNfRVhT37PdzvszB43fCaclJWq8pu1+/OPe1bR9cbsd3/PhJOvnwk7994Q3rd/X7hxTb8BfOO9Ys+TWd/Sf2aL/Abu7Pdt55SyVb0fvyFYe04e3J6ssi2sf0OQ3y/29W987Ml5pyoA53hM+3zszLTeEoKo9jcfYfrIZicCF9SbNykTgOUJHUWicYF9tQTgJfqbG0cKAksR6F4A1sca6ypXffTrdAVs9juo4kLT8hYE4J+9+U5o+i4SgNXHc1feCWEq9mZC4JV3wrkw/33gTMCa8lp73ZqcxP6mvks7aT92AWy3AKwrfqe/dz2N/ZnYf78IofmydYiZTfpYx/zbccXHmbBrHve+7H7bZ5vpdfg/9vhv/qV4qc+yZCvjPzcAqoJzbDfEqlhQBgEIQAACEIAABCAwPAJj+77L9R/Xf8M7iut7lGL8e+HW5+t659ut4qsIpjfuF2HUPO5//1QkLTDo5GOTxxhP6t8QPvTYk+Hk9JHDudXBjQRNETMnorI8KlnHEMG27DUTq7X+1PbG9TO7dWzd3hBunIm/0nOBwFo2YAmHTDj/uFmRXFJv0m25ALxrJXHWoMC+mgJw7f7K/GU/BBYQ2LOgfFfxqo+AzsSamegbQjh1ITx0RYZRUexQ0FXA2eBNymuKm3WEIxGArv7jO43f0n73OCruhV1imP4W8LxNW3Xzj3qej5ffvw7/xy6AWQF4LuxODq3J7z9r7M/nWkrzZfl5KZuvde9fx/znbdJHvk/813+AmP8WeN393fBYh/9jj/9VvhRPo6HXG/znBkBVAI/thlgVC8ogAAEIQAACEIAABIZHYGzfd7n+4/pveEdxfY9SjH8v3Pp8Xe98uxR9revLrF6lADqrRQICEOg5gaUF4Cb+ykkyLwJZ8UYFIRXBbJmkVy33/S2XFwHopz9/u/Fb2pf7vpwtMfpZh/9jF8DyAnD6c27jbB3zb/vrW3od/o89/gfxpbjJB9+0Df5zA6AqfMZ2Q6yKBWUQgAAEIAABCEAAAsMjIN9333777fCLX/wi/PKXvwy/+tWvsvfwPJ14xPUf139Dje06fqUY/
Сочетания сводных, ВПР и устранения дубликатов вообще чаще всего достаточно для большинства подобных задач.
Во втором варианте, у меня выводится только 2 столбца "Сумма по полю цена" с перечислением товаров и объединенные суммы старого и нового прайса. Подскажите, как вывести отдельно в разных столбах эти два параметра (старый и новый прайс).
Помимо своих данных, создала тестовую таблицу как в описании - тоже самое, выводятся объединенные данные.
Не подскажете, как с помощью Power Query способом №3 синхронизировать данные из двух отдельных файлов (т.е. данные находятся не в одной таблице, а в двух отдельных файлах)?
Скачала пример. В результате после всех действий с power query происходит следующее: в последней таблице (в Вашем описании) отсутствуют нулевые строки в столбце старый товар. Т.е. я не могу выявить товар, который был добавлен в новом прайсе (киви, ячмень, чеснок и пр я не вижу в таблице совсем). Эксель 2016. При этом если я открываю Вашу вкаладыку в скаченном файле то эксель "ругается" на несовместимость. Какие действия надо совершить чтобы можно было увидеть товар, который был добавлен (киви, ячмень и пр). Спасибо!
для полного счастья мне не хватает в варианте Сводная столбца СТАТУС.
В статью вкралась небольшая ошибка в Способ 1. Сравнение таблиц функцией ВПР (VLOOKUP):
Вместо "Минусы тоже есть. Для поиска добавленных в новый прайс товаров ..."
должно быть "Минусы тоже есть. Для поиска удаленных из старого прайса товаров ..."
Решил сравнить 2 таблицы по 3 варианту. Офис установлен 16, т.е. Power Query уже встроенный.
Казалось бы всё получилось на отлично, если бы не внимательный взгляд, который нашёл проблемы:
В обеих таблицах есть столбец в котором указан процент с дробной частью, например 14,9999955882366%
Для красивого вывода в формате ячеек указан показ только 2х нулей после запятой. В итоге в ячейке отображается цифра 15,00%.
После выполнения всех запросов в новой таблице, в которой уже присутствуют оба эти столбца отображается цифра 0,149999955882366 без знака %.
Так вот, всё бы хорошо, но в дополнительном столбце, в котором я делаю проверку, образно A<>B, вывести "не равно", в некоторых позициях именно с этим значением, и отображается "не равно", хотя оба числа одинаковые.
Если в соседнем столбце написать формулу Если (А1=B1;"OK";"Не равно"), то она выдаёт "ОК". Т.е. эта формула видит, что оба значения одинаковые. Но, при этом Power Query говорит обратное. Что не так, где и что ещё можно проверить?
Проблема не во всех строках, а только в некоторых. Пробовал на разных компах с разной версией Excel
. Так как она длинная, я скрыл не интересующие нас столбцы и порезал её на куски.
Думаю копать нужно где-то в этом направлении. Почему после объединения Эксель сделал не 2, а 4 строки.
Я не знаю как Вас благодарить, бесценный Вы наш!!!!!!
это прекрасно!
Спасибо!