Динамические массивы в Excel
Что такое динамические массивы
В сентябре 2018 года Microsoft выпустила обновление, которое добавляет в Microsoft Excel совершенно новый инструменты: динамические массивы (Dynamic Arrays) и 7 новых функций для работы с ними. Эти вещи, без преувеличения, совершенно кардинальным образом меняет всю привычную технику работы с формулами и функциями и касаются, буквально, каждого пользователя.
Рассмотрим простой пример, чтобы объяснить суть.
Предположим, что у нас есть простая табличка с данными по городам-месяцам. Что будет если мы выделим любую пустую ячейку справа на листе и введем в нее формулу-ссылку не на одну ячейку, а сразу на диапазон?
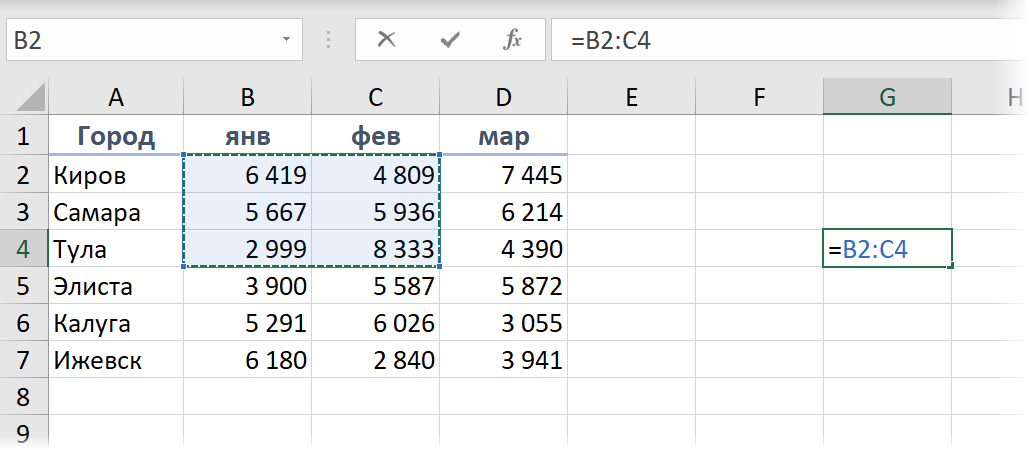
Во всех прошлых версиях Excel после нажатия на Enter мы бы получили содержимое только одной первой ячейки B2. А как иначе?
Ну, или можно было бы завернуть этот диапазон в какую-нибудь аггрегирующую функцию типа =СУММ(B2:C4) и получить по нему общий итог.
Если бы нам потребовались операции посложнее примитивной суммы, например, извлечение уникальных значений или Топ-3, то пришлось бы вводить нашу формулу как формулу массива, используя сочетание клавиш Ctrl+Shift+Enter.
Теперь всё по-другому.
Теперь после ввода такой формулы мы можем просто нажать на Enter - и получить в результате сразу все значения, на которые мы ссылались:
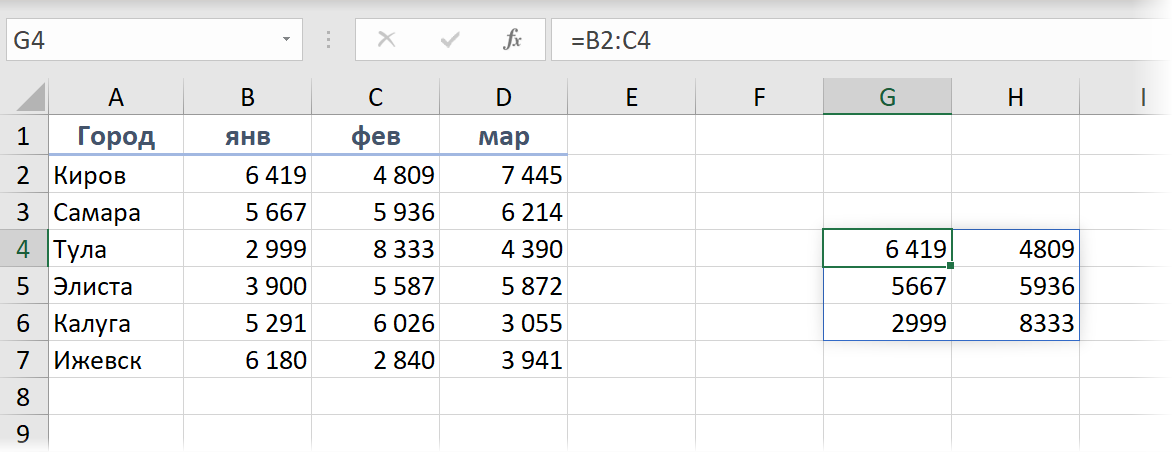
Это не магия, а новые динамические массивы, которые теперь есть в Microsoft Excel. Добро пожаловать в новый мир :)
Особенности работы с динамическими массивами
Технически, весь наш динамический массив хранится в первой ячейке G4, заполняя своими данными необходимое количество ячеек вправо и вниз. Если выделить любую другую ячейку массива, то в строке формул ссылка будет неактивной, показывая, что мы находимся в одной из "дочерних" ячеек:
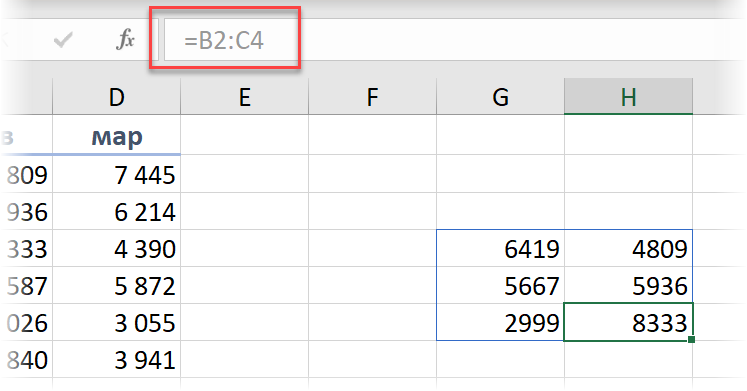
Попытка удалить одну или несколько "дочерних" ячеек ни к чему не приведёт - Excel тут же заново их вычислит и заполнит.
При этом ссылаться на эти "дочерние" ячейки в других формулах мы можем совершенно спокойно:
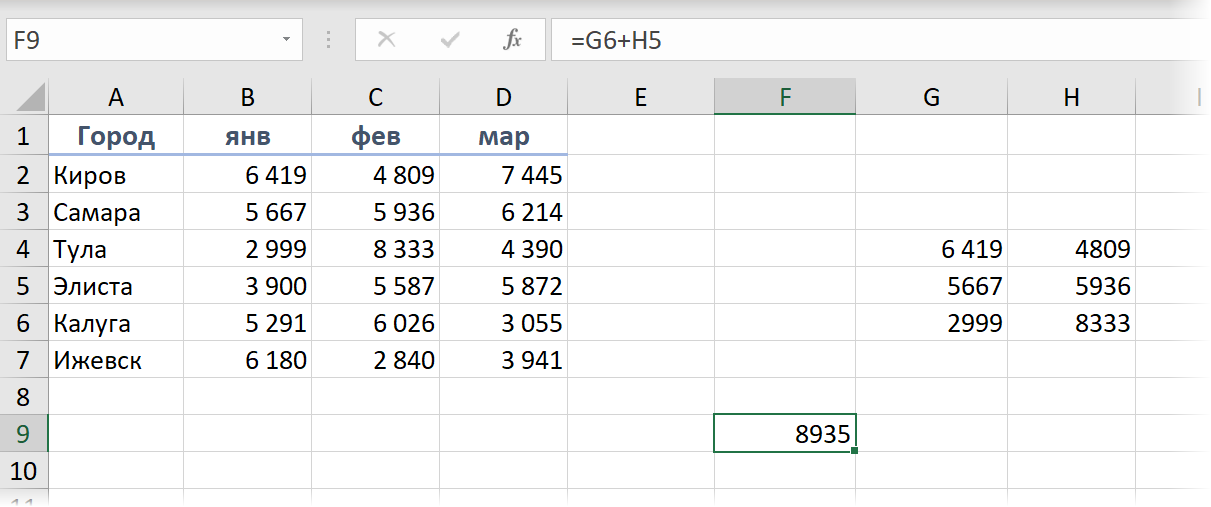
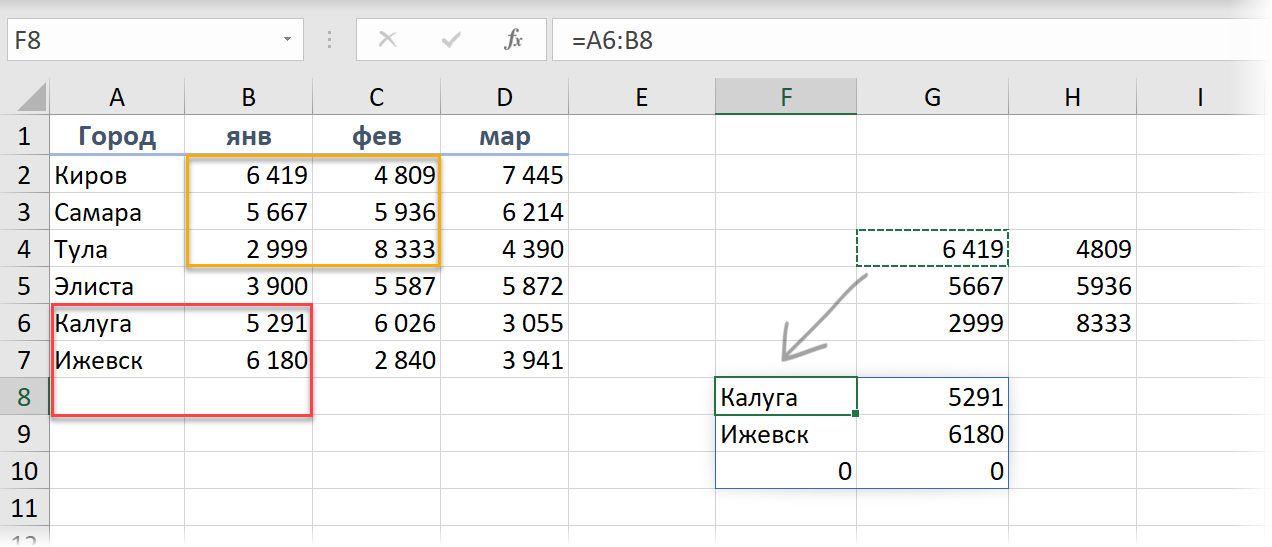
Если нам нужно переместить массив, то достаточно будет перенести (мышью или сочетанием Ctrl+X, Ctrl+V), опять же, только первую главную ячейку G4 - вслед за ней перенесется на новое место и заново развернётся весь наш массив.
Если вам нужно сослаться где-нибудь еще на листе на созданный динамический массив, то можно использовать спецсимвол # ("решётка") после адреса его ведущей ячейки:
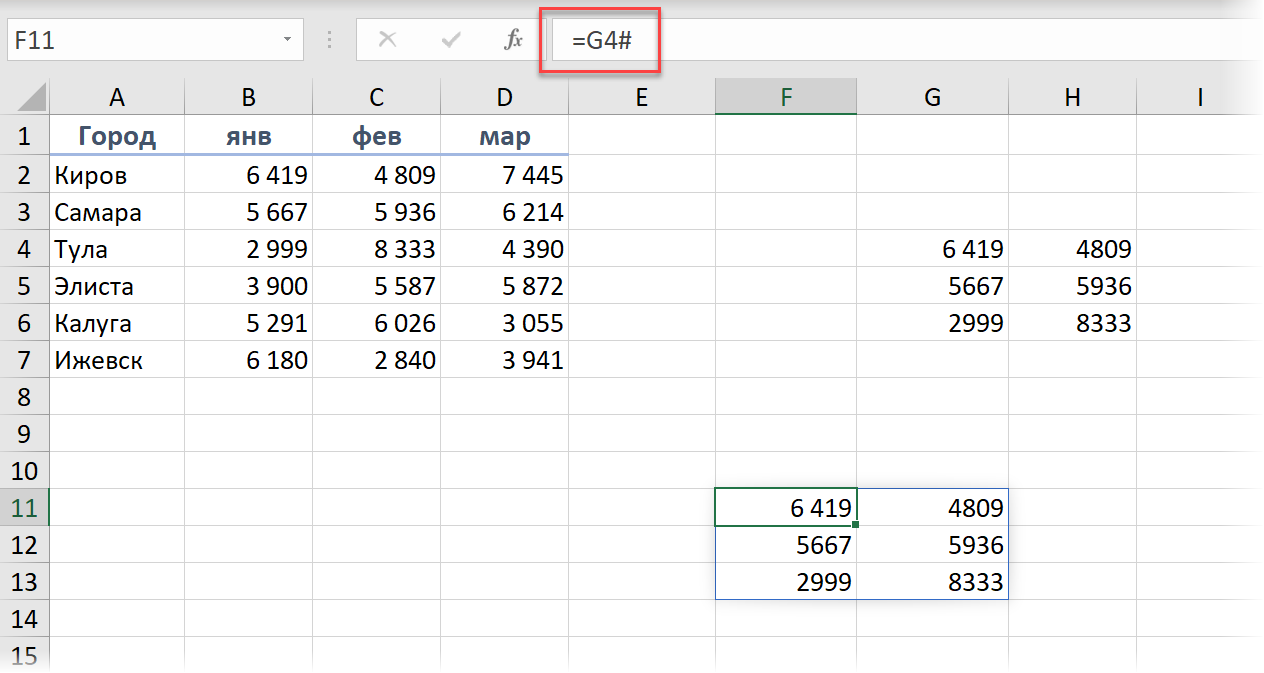
Например, теперь можно легко сделать выпадающий список в ячейке, который ссылается на созданный динамический массив:
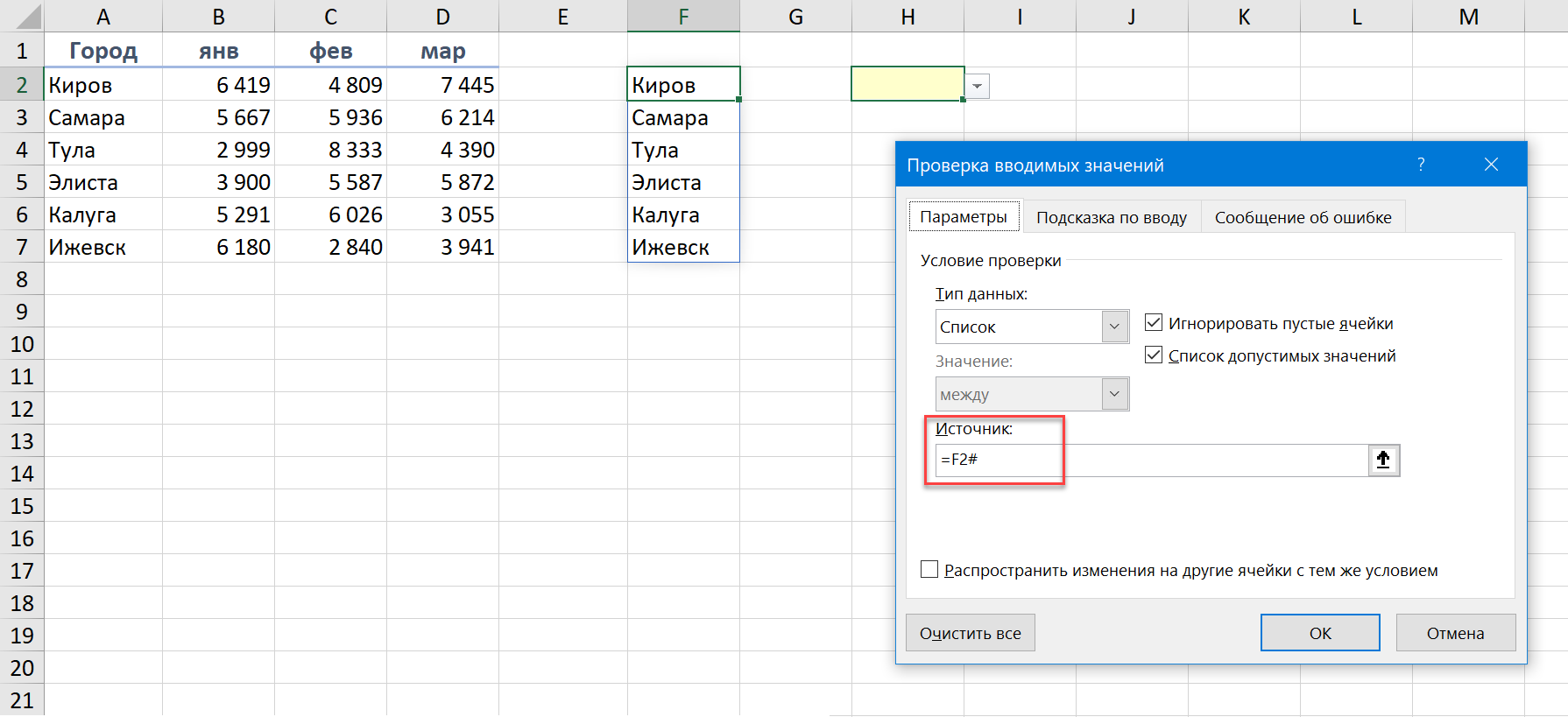
Ошибки динамических массивов
Но что будет, если для развёртывания массива не будет достаточно пространства или на его пути окажутся ячейки уже занятые другими данными? Знакомьтесь с принципиально новым типом ошибок в Excel - #ПЕРЕНОС! (#SPILL!):
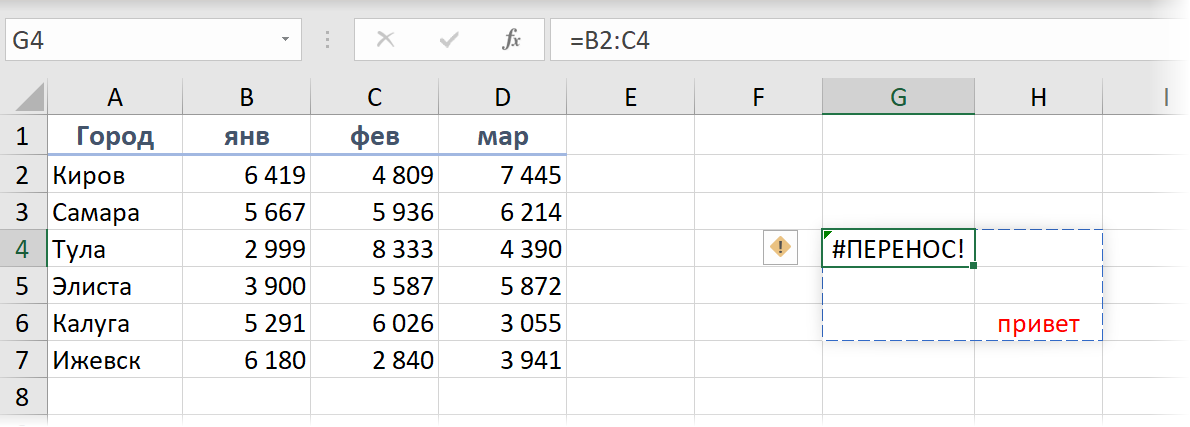
Как всегда, если щелкнуть мышью по значку с желтым ромбом и восклицательным знаком, то мы получим более подробное пояснение по источнику проблемы и сможем быстро найти мешающие ячейки:
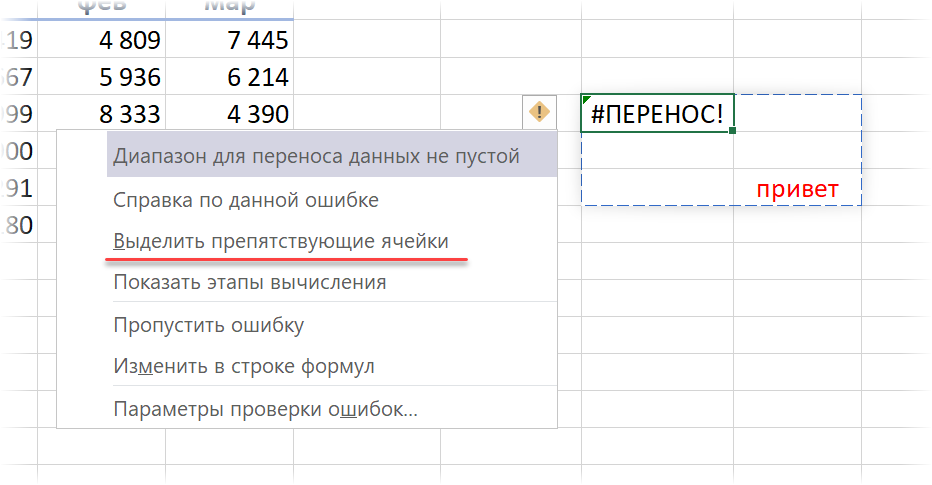
Аналогичные ошибки будут возникать, если массив выходит за пределы листа или натыкается на объединенную ячейку. Если удалить препятствие, то всё тут же исправится на лету.
Динамические массивы и "умные" таблицы
Если динамический массив указывает на "умную" таблицу, созданную сочетанием клавиш Ctrl+T или с помощью Главная - Форматировать как таблицу (Home - Format as Table), то он также унаследует её главное качество - автоподстройку размеров.
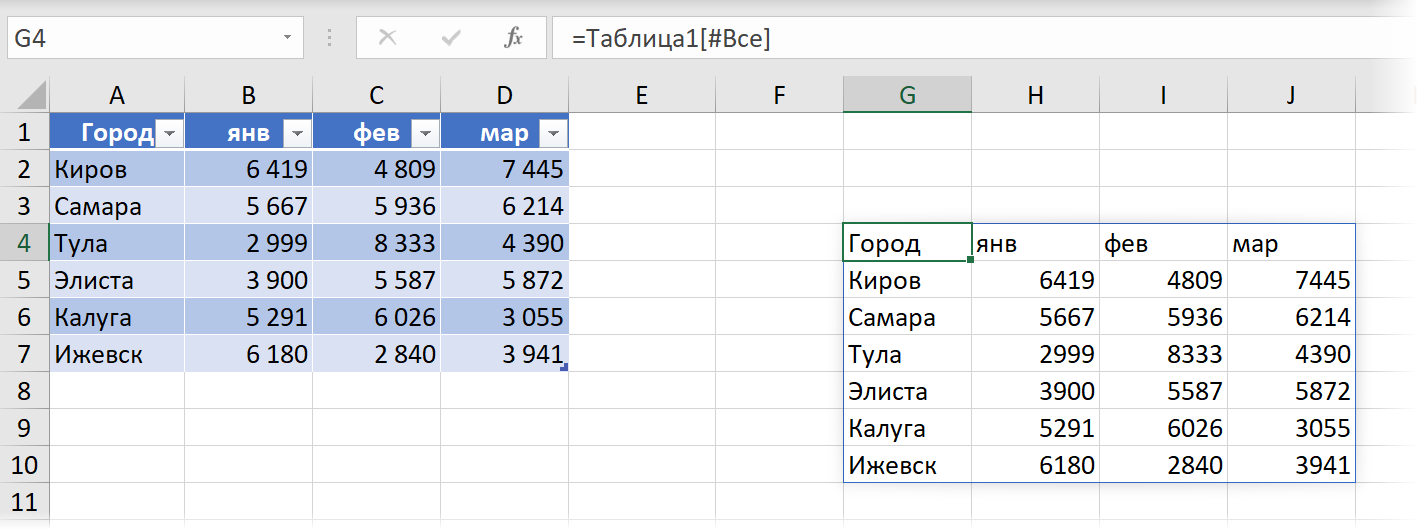
При добавлении новых данных внизу или справа "умная" таблица и динамический диапазон тоже будут автоматически растягиваться:
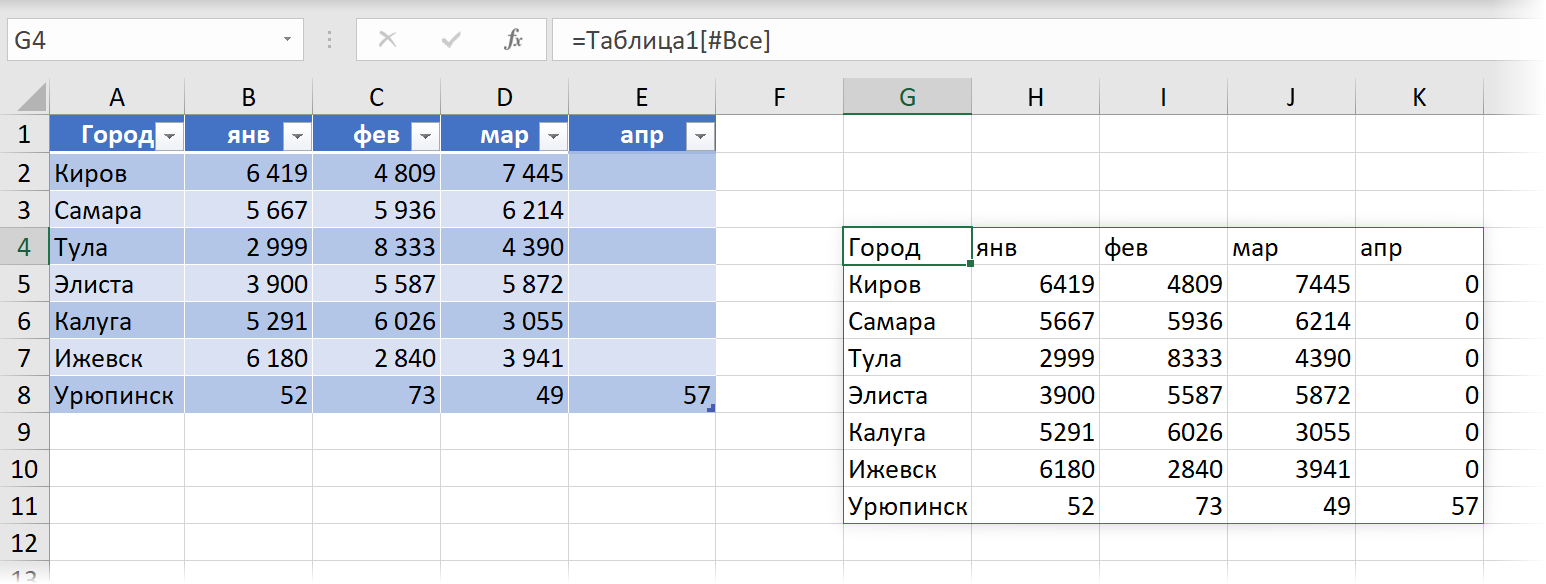
При этом, однако, есть одно ограничение: мы не можем использовать ссылку на динамический диапазон в форумулах внутри "умной" таблицы:
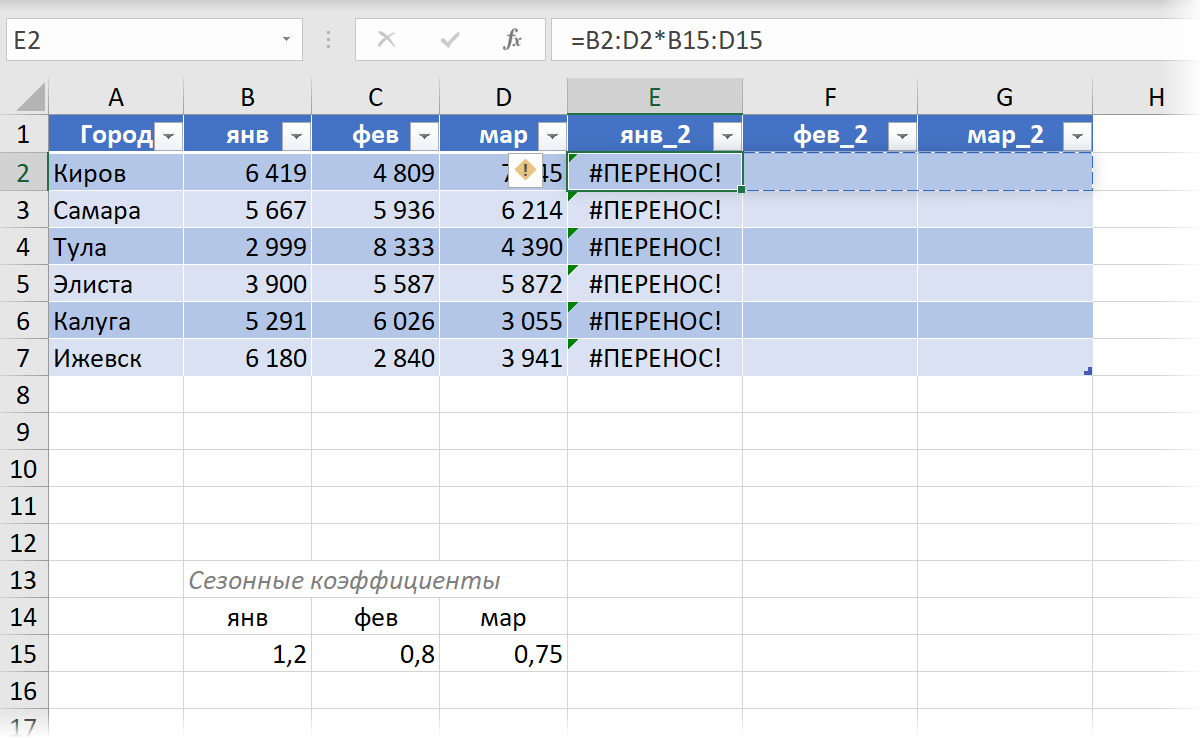
Динамические массивы и другие функции Excel
Хорошо, скажете вы. Всё это интересно и забавно. Не нужно, как раньше, вручную протягивать формулу со ссылкой на первую ячейку исходного диапазона вниз и вправо и всё такое. И всё?
Не совсем.
Динамические массивы - это не просто еще один инструмент в Excel. Теперь они внедрены в самое сердце (или мозг) Microsoft Excel - его вычислительный движок. А это значит что и другие, привычные нам формулы и функции Excel теперь тоже поддерживают работу с динамическими массивами. Давайте разберём несколько примеров, чтобы вы осознали всю глубину произошедших изменений.
Транспонирование
Чтобы транспонировать диапазон (обменять местами строки и столбцы) в Microsoft Excel всегда имелась встроенная функция ТРАНСП (TRANSPOSE). Однако, чтобы её использовать, вы должны были сначала правильно выделить диапазон для результатов (например, если на входе был диапазон 5х3, то вы должны были обязательно выделить 3x5), потом ввести функцию и нажать сочетание Ctrl+Shift+Enter, т.к. она умела работать только в режиме формул массива.
Теперь можно просто выделить одну ячейку, ввести в нее эту же формулу и нажать на обычный Enter - динамический массив сделает всё сам:
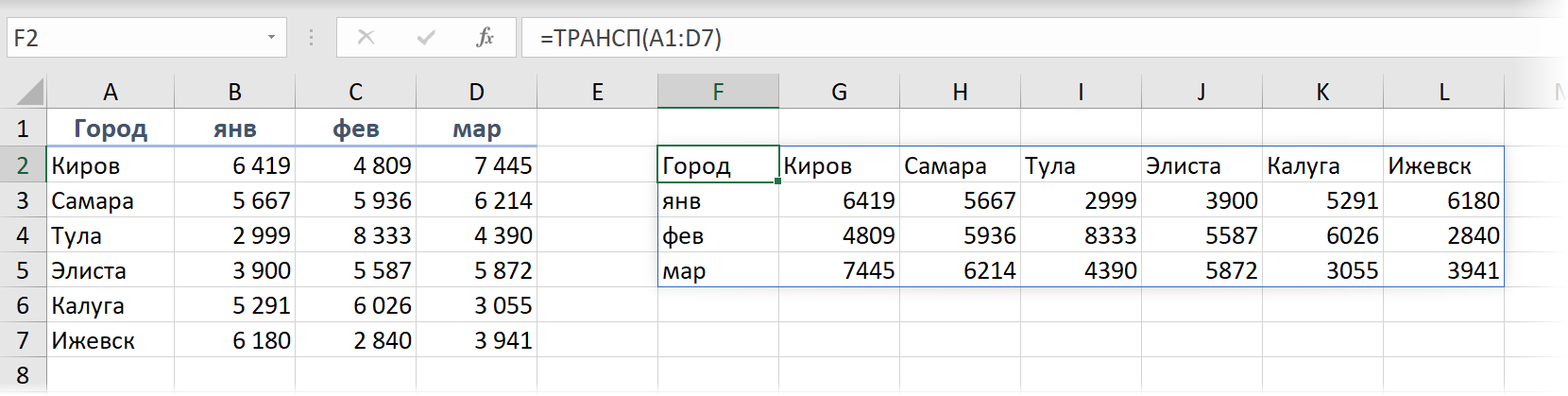
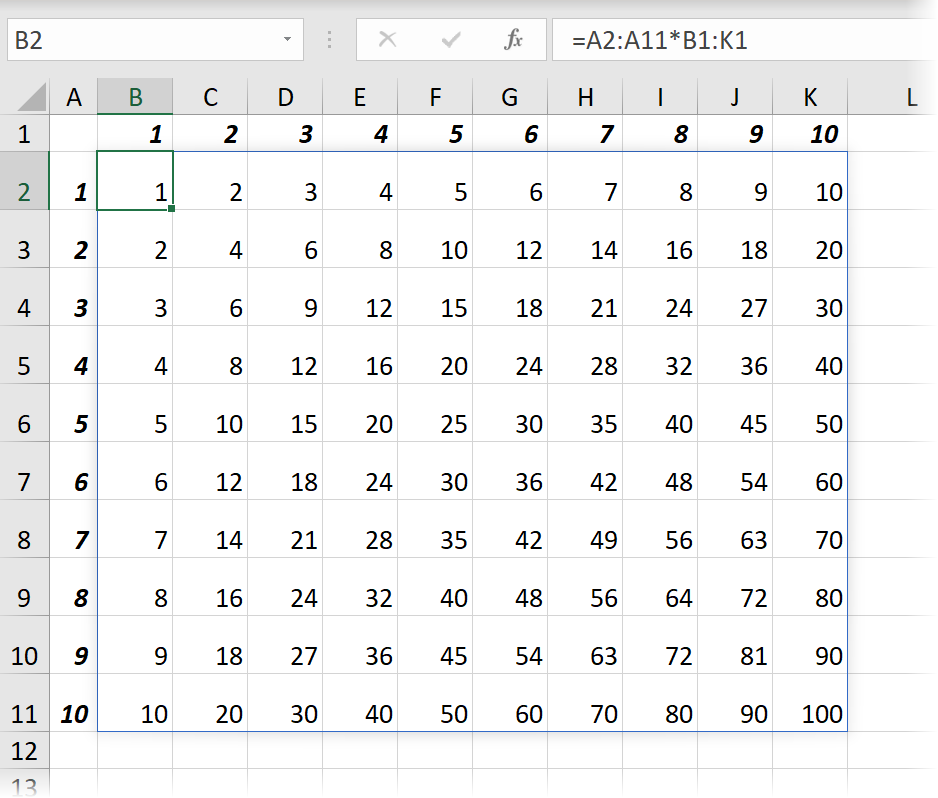
Таблица умножения
Этот пример я обычно приводил, когда меня просили наглядно показать преимущества формул массива в Excel. Теперь чтобы посчитать всю таблицу Пифагора достаточно встать в первую ячейку B2, ввести туда формулу перемножающую два массива (вертикальный и горизонтальный набор чисел 1..10) и просто нажать на Enter:
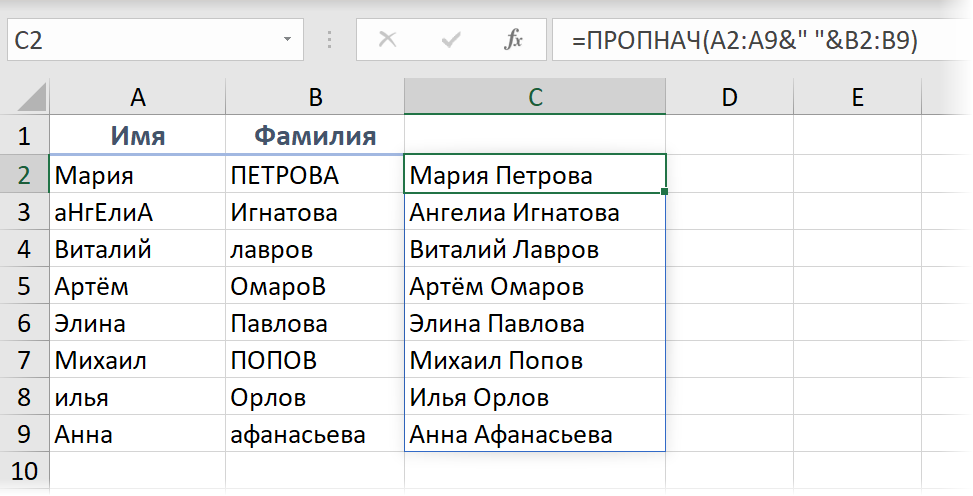
Склейка и преобразование регистра
Массивы можно не только перемножать, но склеивать стандартным оператором & (амперсанд). Предположим, нам нужно сцпеить имя и фамилию из двух столбцов и поправить скачущий регистр в исходных данных. Делаем это одной короткой формулой, которая формирует весь массив, а потом применяем к нему функцию ПРОПНАЧ (PROPER), чтобы привести в порядок регистр:
Вывод Топ-3
Предположим, что у нас есть куча чисел, из которых нужно вывести три лучших результата, расположив их в порядке убывания. Теперь это делается одной формулой и, опять же, без всяких Ctrl+Shift+Enter как раньше:
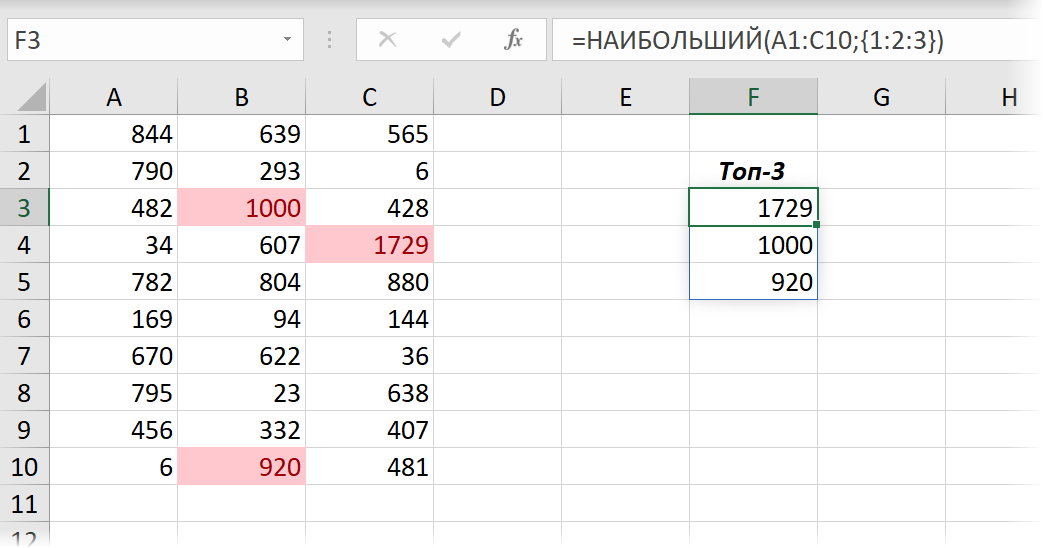
Если захочется, чтобы результаты располагались не в столбец, а в строку, то достаточно заменить в этой формуле двоеточия (разделитель строк) на точку с запятой (разделитель элементов внутри одной строки). В англоязычной версии Excel роль этих разделителей играют точка с запятой и запятая, соответственно.
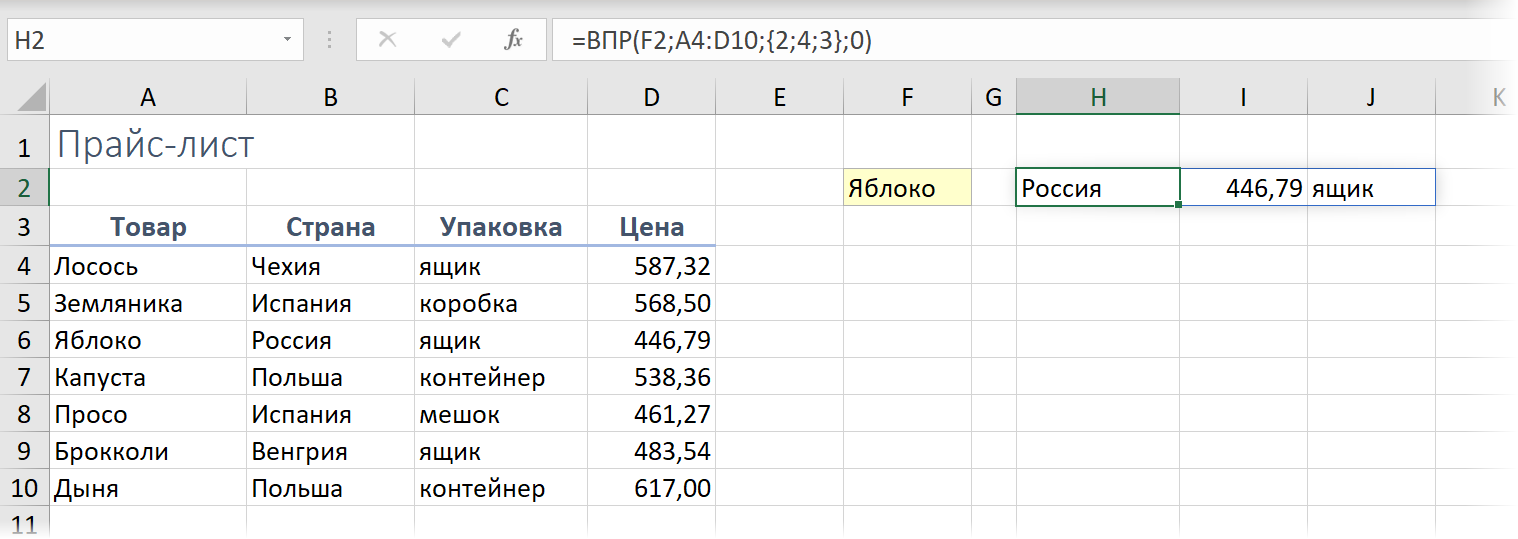
ВПР извлекающая сразу несколько столбцов
Функцей ВПР (VLOOKUP) теперь можно вытаскивать значения не из одного, а сразу из нескольких столбцов - достаточно указать их номера (в любом желаемом порядке) в виде массива в третьем аргументе функции:
Функция СМЕЩ (OFFSET) возвращающая динамический массив
Одной из самых интересных и полезных (после ВПР) функций для анализа данных является функция СМЕЩ (OFFSET), которой я посвятил в своё время целую главу в своей книжке и статью здесь. Сложность в понимании и освоении этой функции всегда была в том, что она возвращала в качестве результата массив (диапазон) данных, но увидеть его мы не могли, т.к. Excel до сих пор не умел работать с массивами "из коробки".
Сейчас эта проблема в прошлом. Посмотрите, как теперь с помощью одной формулы и динамического массива, возвращаемого СМЕЩ, можно извлечь все строки по заданному товару из любой отсортированной таблицы:
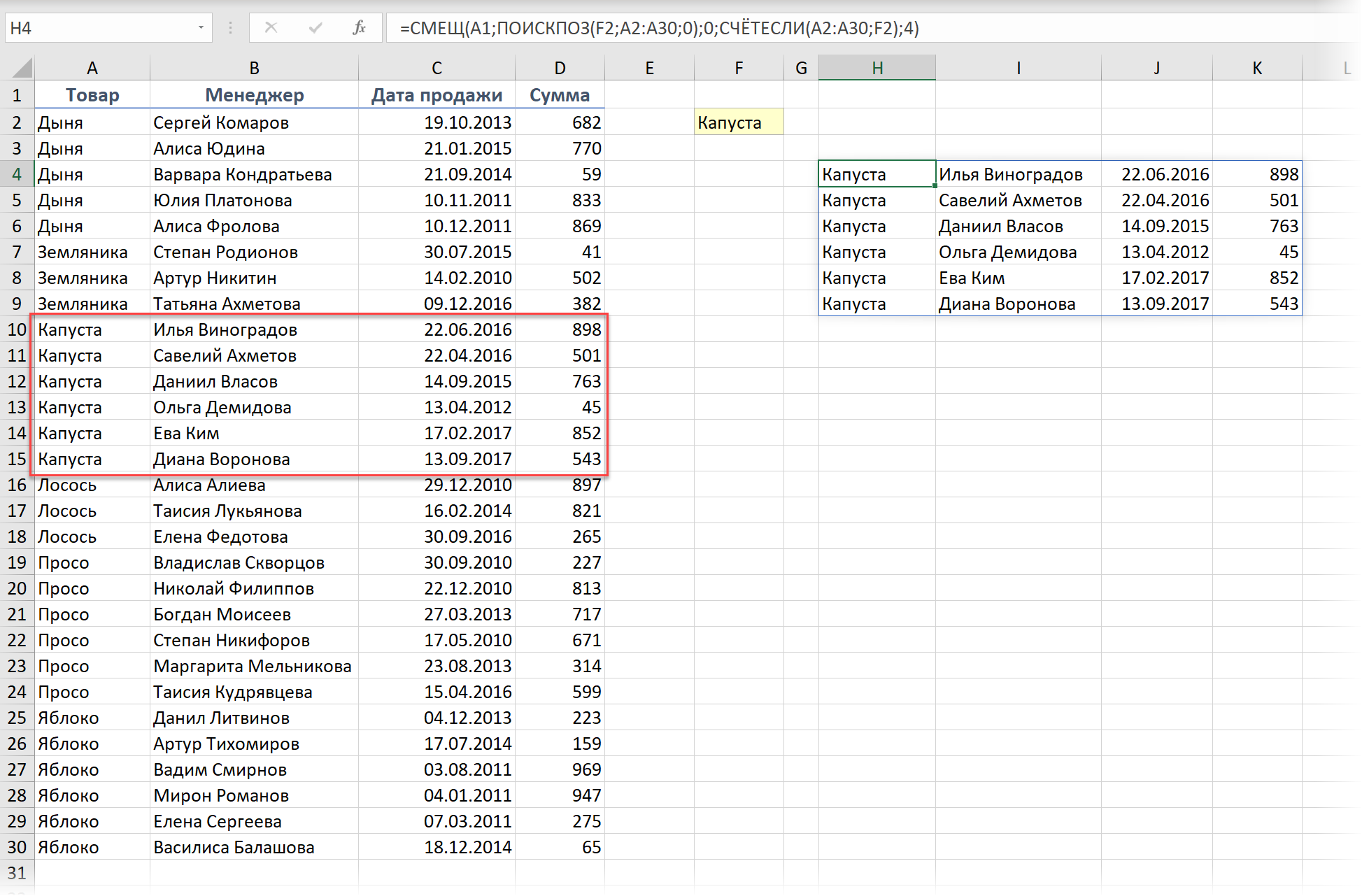
Давайте разберём её аргументы:
- А1 - стартовая ячейка (точка отсчёта)
- ПОИСКПОЗ(F2;A2:A30;0) - вычисление сдвига от стартовой ячейки вниз - до первой найденной капусты.
- 0 - сдвиг "окна" вправо относительно стартовой ячейки
- СЧЁТЕСЛИ(A2:A30;F2) - вычисление высоты возвращаемого "окна" - количества строк, где есть капуста.
- 4 - размер "окна" по горизонтали, т.е. выводим 4 столбца
Новые функции для динамических массивов
Помимо поддержки механизма динамических массивов в старых функциях, в Microsoft Excel были добавлены несколько совершенно новых функций, заточенных именно под работу с динамическими массивами. В частности, это:
- СОРТ (SORT) - сортирует входной диапазон и выдает динамический массив на выходе
- СОРТПО (SORTBY) - умеет сортировать один диапазон по значениям из другого
- ФИЛЬТР (FILTER) - извлекает из исходного диапазона строки, удовлетворяющие заданным условиям
- УНИК (UNIQUE) - извлекает из диапазона уникальные значения или убирает повторы
- СЛМАССИВ (RANDARRAY) - генерит массив случайных чисел заданного размера
- ПОСЛЕД (SEQUENCE) - формирует массив из последовательности чисел с заданным шагом
Подробнее про них - чуть позже. Они стоят отдельной статьи (и не одной) для вдумчивого изучения :)
Выводы
Если вы прочитали всё написанное выше, то, думаю, уже осознаёте масштаб изменений, которые произошли. Очень многие вещи в Excel теперь можно будет делать проще, легче и логичнее. Я, признаться, немного в шоке от того, сколько статей теперь придется корректировать здесь, на этом сайте и в моих книгах, но готов это сделать с легким сердцем.
Подбивая итоги, в плюсы динамических массивов можно записать следующее:
- Можно забыть про сочетание Ctrl+Shift+Enter. Теперь Excel не видит различий между "обычными формулами" и "формулами массива" и обрабатывает их одинаково.
- Про функцию СУММПРОИЗВ (SUMPRODUCT), которую раньше использовали для ввода формул массива без Ctrl+Shift+Enter тоже можно забыть - теперь достаточно просто СУММ и Enter.
- Умные таблицы и привычные функции (СУММ, ЕСЛИ, ВПР, СУММЕСЛИМН и т.д.) теперь тоже полностью или частично поддерживают динамические массивы.
- Есть обратная совместимость: если открыть книгу с динамическими массивами в старой версии Excel, то они превратятся в формулы массива (в фигурных скобках) и продолжат работать в "старом стиле".
Нашлось и некоторое количество минусов:
- Нельзя удалить отдельные строки, столбцы или ячейки из динамического массива, т.е. он живёт как единый объект.
- Нельзя сортировать динамический массив привычным образом через Данные - Сортировка (Data - Sort). Для этого есть теперь специальная функция СОРТ (SORT).
- Динамический диапазон нельзя превратить в умную таблицу (но можно сделать динамический диапазона на основе умной таблицы).
Само-собой, это еще не конец и, я уверен, Microsoft продолжит совершенствовать этот механизм в будущем.
Где скачать?
И, наконец, главный вопрос :)
Microsoft впервые анонсировало и показало превью динамических массивов в Excel еще в сентябре 2018 года на конференции Ignite. В последующие несколько месяцев происходило тщательное тестирование и обкатка новых возможностей сначала на кошках сотрудниках самой Microsoft, а потом на добровольцах-тестировщиках из круга Office Insiders. В этом году обновление, добавляющее динамические массивы стали постепенно раскатывать уже по обычным подписчикам Office 365. Я, например, получил его только в августе с моей подпиской Office 365 Pro Plus (Monthly Targeted).
Если в вашем Excel ещё нет динамических массивов, а поработать с ними очень хочется, то есть следующие варианты:
- Если у вас подписка Office 365, то можно просто продождать, пока до вас дойдет это обновление. Как быстро это случится - зависит от настройки частоты доставки обновлений для вашего Office (раз в год, раз в полгода, раз в месяц). Если у вас корпоративный ПК, то можно попросить вашего администратора настроить загрузку обновлений почаще.
- Можно записаться в ряды тех самых добровольцев-тестировщиков Office Insiders - тогда вы будете первым получать все новые возможности и функции (но есть шанс повышенной глючности в работе Excel, само-собой).
- Если у вас не подписка, а коробочная standalone-версия Excel, то придется ждать до выхода следующей версии Office и Excel в 2022 году, как минимум. Пользователи таких версий получают только обновления безопасности и исправления ошибок, а все новые "плюшки" теперь достаются только подписчикам Office 365. Sad but true :)
В любом случае, когда динамические массивы появятся в вашем Excel - после этой статьи вы будете к этому уже готовы :)
Ссылки по теме
- Что такое формулы массива и как их использовать в Excel
- Суммирование по окну (диапазону) с помощью функции СМЕЩ (OFFSET)
- 3 способа транспонировать таблицу в Excel

Интересно, это сколько новых идей и практического применения вызовет использование динамических массивов?
Николай, на счёт переписать 2-ю книжку Вы, конечно, пошутили... Или нет?
Вначале говорю Вам Спасибо, за такую замечательную новость!
И хочу спросить - какая у Вас версия Excel сейчас? Сегодня купил Office 365 (правда пока проверил на MacOS) - нет динамических массивов
Моя версия Excel 16.29 (19090802)
Кстати, для Мака их может еще и не быть.
Напишите пожалуйста какая у вас версия офиса и сборка.
PS: Я правильно понимаю, что эта ваша версия в рамках подписки и вы не состоите в Office Insider?
Не Office Insider
Достучался через IT до Microsoft, сказали что для нас добавление новых функций запланировано на конец Q1'2020.
Теперь в томительном ожидании.
Которая сильно запаздывает и пропускает некоторые версии.
Например мы с версии 19.02 сразу идем в 19.08, а потом 19.09 которую нам должны накатить только в конце июня 2020.
Октябрь 2020 замечательный месяц, нам наконец то накатили обновление в котором есть динамические массивы.
Была 1908 и сейчас нам поставили 2002.
В итоге вместо Q1'20 все сместилось на Q4'20
PS: Немного поправлю функция "НАИБОЛЬШИЙ" в английской версии "LARGE"
PPS: Да версия конечно же у нас не отдельная
у меня Microsoft Office 365 ProPlus
Версия 1909 (сборка 12026.20264) Monyhly Channel
Если смотреть "о программе Excel" то Microsoft Excel для Office 365 MSO (16.0.12026.20100) 32-разрядная
новых плюшек до сих порт нет.
ЗЫ. Можете попробовать пнуть админов, чтобы переключили вас на Monthly (Targeted) канал обновлений. Если это у вас возможно и приемлемо. Всётаки, Targeted-каналы - это всё ещё тестовые версии, которые не обязаны быть стабильными.
Офис купил только после просмотра Вашего видео, до этого у меня стоял ломанный Excel 2016.
Чем я обидел майкрасофт??? Почему мне не дают эту "магию". И почему Вы работаете на благо и приводите клиентов, а Майкрасофт Вас подводит???
Есть ли Excel способ задать какие либо ограничения по округлений данных по месяцам, чтобы их сумма не превышала или не была ниже заданного округлённого годового значения?
Спасибо
Как объединить два и более динамических массива в один?
Имеется номенклатура в нескольких столбцах, хотел построить отсортированный список без дубликатов динамическим массивом
Можно собрать одну таблицу с нескольких листов при помощи динамических массивов?
Спасибо!
Не могу только решить одну, часто встречающуюся у меня в работе, задачу.
Есть 2 массива с одинаковым количеством столбцов. В первом 1 строка, а во втором может быть очень много. Нужно на выходе получить массив, в котором в каждой строке должен получиться сумма произведений строки из первого массива и поочередно строк второго.
Уже все перепробовал, возможно есть способ. Заранее спасибо за ответ.
При использовании динамических массивов столкнутся с проблемой, когда при розшаревании файла все формулы с динамическими массивами превращаются в обычные формулы массивов.
Не могу найти никакой информации по этому вопросу. Как это влияет на производительность и можно ли этого избежать.
Может вы что-то подскжете?
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAa4AAAHaCAYAAABYRq1NAAAgAElEQVR4Aey9Z3dcx5U2ii933ftt5ifMP7jzzryvZsgZjz0zHlvO9ki2ZEUqQTkny5aVLEu2EqlEMWcQGQRAIhI555w650YnJAZJ9ty1nrt21anT1QfdjQZJQAC5udbmOafCrr2f2r2fU3VON/LA/xgBRoARYAQYgW2EQN42spVNZQQYAUaAEWAEwMTFQcAIMAKMACOwrRBg4tpW08XGMgKMACPACDBxcQwwAowAI8AIbCsEmLi21XSxsYwAI8AIMAJMXBwDjAAjwAgwAtsKASaubTVdbCwjwAgwAowAExfHACPACDACWwQBj8eDv/u7v0NeXp6Q73znO1haWtoi1mU3g2weGhrK2IjqqM21+HeFWmqRn7cTexzXwoStpCOTX5nKr5XtG63/WtnJehgBRmAjEWhtbcXrr78uyOrMmTMi0e/evXsjh7xmuomY/q//+/9JS17Z6q7EgOzE5diDnQbzizuA/FpjjG8m0dbm52GnhS0de3Yib+cepHBobT7yTFvXA0smvzKVr0d3trYbrT/b2FzHCDACWxWBv//7vxdEtlXts9qVjqDSlVn7rfc6M3EJ0kpdVTn27IGkrm8o0RIhpZCUA3t27sTOnfmGXdL9dASXGzCZ/MpUnpvWtVtttP61LeAWjAAjsLUQoJUWLRhGR0e3lmFrWKMTlX6+Rrd1VWcnrhSS0PUaibY2uSJLWQkRwWgrteTix9LP1E8EJPd087JuQVJ/naRqkb9zD/bk52HVGMYSjEjMtMUcj3xJZ4tRltKXxrO0Fb7pdkhsMo+1Vn36cXXE+ZwRYARuHASOHj0q8hYdt+M/RViZtg6v1qfMxAWDTFKSvRqOEm1ecvUjiEolcgf25Gtbdyl1ln6GOpHwFfPQSi/tmNRY2qSaojZfbh2qo2iS7G/dRkwZR5CR5oOwJUkgom9yoFR/yRLLFqX1OnWs1e1T6zONawDEB0aAEbihEPjbv/1bbJdnW+km5hskLmmOSMg6SYniZKKVrazXuit6nX6u2ljL5Paf5VGWaiwIQ63uKPkLbtHILkk4Vr2kgsoUwWaq34k9e6zPyLK0FauzTPVrjWWpXzWu6TafMAKMwA2EAO0S0Ysa2/GfIi066ufX0pcsK67UYSSBWRKt+UZEauI2yc7cLlTPylLbyRGoTNvOE+eqfaoN4sokKSI4ZU+S7EwySyEppUcfXz/X68kWpVcvt9qUHDOVENP1obGy6VQYWNsoXXxkBBiBGwkBIi16NX67/UtHVOnKrtavnIkrdZvOmvS161UvUGh16lmRSXhkvl6fizsGYdDzNXMrD5CERbpU8k+nN5f6ndgjnt0pPZlszEWX0pGjLavGzQUPbsMIMALXGwL0Svx2W3FlI6hsdVcyd5mJS39uJDTryVc/p0rt2kJccvWlVitaO83a1Oc9WkWGU2q/k94m1PcTxbj0hmHy+ZrQa702yS6dLVpZumdzZl9JlPor99nHMtrnYkvKuBkA4GJGgBG4rhGgrcJdu3ZtKx/JZiKoTP+ojtpci39ZtNDKJnULL5m3tQQvrNCvU/vt3LNH+7Ky3k43n8q1sbQEr7cyz0VyV2SoSqWOFDIjSl3rrcIsqz+15Zlfa9hNz6CUnWlszDyWtDFzfSoualzlGR8ZAUaAEWAEkghkIa5kIz5jBBgBRoARYAS2CgJMXFtlJtgORoARYAQYgZwQYOLKCSZuxAgwAowAI7BVEGDi2iozwXYwAowAI8AI5IQAE1dOMHEjRoARYAQYga2CABPXVpkJtoMRYAQYAUYgJwSYuHKCiRsxAowAI8AIbBUEmLi2ykywHYwAI8AIMAI5IcDElRNM3IgRYAQYAUZgqyDAxLVVZoLtYAQYAUaAEcgJASaunGDiRowAI8AIMAJbBYG85eVlsDAGHAMcAxwDHAPbJQaYuJi4+caFY4BjgGNgW8UAExcH7LYK2O1yR8h28uqFY2DjYoCJi4mLiYtjgGOAY2BbxQATFwfstgpYvovduLtYxpax3S4xwMTFxMXExTHAMcAxsK1igImLA3ZbBex2uSNkO3n1wjGwcTHAxMXExcTFMcAxwDGwrWIgI3HZbDawrI0B31Vt3F0VY8vYcgxwDKSLgazEtVW+Jb1V7SBiTwcql/GHjWOAY4BjYONigInrKliRV6Rrr0iZ3Dfuw8uJkbG9UWOAiesqietGDZxc/Wbi4uSaa6xwO46VXGNgXcT1N3/zNyLN36hHK8dxUl77g8YYrY1Rrh9WbsdYcgzIGMiZuBRZWZP3jXKdzn9OymsnEsZobYw4GTFGHAPri4GcietGIaj1+MlJee1gY4zWxoiTFmPEMbC+GMiZuNKtONaT5Ld723T+c1JeO9gYo7Ux4qTFGHEMrC8GciauKyOeWuTn5SFPk/zadJqo3U7scQBw7MFOdW5tmq3O2nYTrjkprx1sjNHaGHHSYow4BtYXAzkTV7oVx9rcoBFS1saZ2mUqz6psQyrT+X8lSbl0Vx7ydpWu8f2vUuzKuwnvjqxvMjc++Ndv15VgtPF+bDVc2R6ec46B9cRAzsR1ZWyQK/Fkapep/Mqsuda91p2UR97FTTftwq6b1iKl9RPEeib9ytuu3651Y8Q/vbPGTQ0nuCuPX8buesEuZ+JKt+JYmwiyEI/Y9pPbiDv37EluFUL1oaO2zSj2GFUdjWyc78k3tyJ3ir1Gw6qM+te2Ol2LdP6vNymPvHsTbnp3BOqYOYjWTxCZdV3LD+v67VovRpvjx7XEhHXxnHEMbHYM5Exc6ZL52mUW8snLh3zEJcvV8y7Hnp3IM59rpSEnevYl/lnr8pCnlNQSgeWiX+m6+uP6kvII3lUrLbHyehcj+uqCygyivundd42tQuqTh12l2gejdBfybpJ9xbajIndz+9Egl3d3mYROZJkMLKlTPXc0dWvj5+XtQqmyTStP2qXZo9plOK4Po9z1Jv3hPowFx8CNFgM5E1e6FcfaqV8nGq01rYZ27oHJR2r1JAr0Pvo59dev9XNLXVb9mh3rOE3n/7qScgpZaSQmEj6RTZKgaEWWp55xEVGZpLQMIiuTbEyy0FdCUpfZh/qbRCRJK5XI6EOv91/GcukusTKU5cnxUuwyx86eNNaFUY46b7QPKfubPcYYnxsPn5yJax05XmtqJRejKiux6H30c+qrX+vnlrqs+jXzrvJ0PUnZuj0oSEARUgqpWYmESEWtgEqxy1htiQ+rICW1naqem1lISCclsXpSurRg11ZVaiUmiC+rXVr/LISzHow4AeWGKePEON3oMZAzcaVbcayd963konpQeR7ULt+VbxUar9ALtfpY2fQrG9Z3TOd/7knZWAWpbT3zaJDIGgShSE8dRdCmkJC+grtS4spAaDpR6iSYhaz0D1XuGHEy0nHjc44HjoHMMZAzca0vzavWkkDMu/i8PJgvUIhnUtlezpA6avONFUWmlzPM/UaduGhxpr+0ob/8oWy7+mPOSVl7LpUMRrltJ7f9JLGpLUCxGlNbhUQQgtjobUSNXHSdgsRyWHEtZ9sqzDO2B/VgWcOuHMgrZ4xy0JXETreRzxkXjoEbLQZyJq50K46rT/2bpIG2Ds0XN65szHT+55qU6bnU6udKy+LtwtRnUZKkV78EIQnHbCuSvFFGq7eUV+yzrLhEP0lG6mZCkaUgR3MlqH3XTNuOXG3X2gkjV4xutA8e+7t27DBGjFGmGMiZuK4s3W+NXmLVlvIyyLWxi5Py2h8sxmhtjDJ9OLmcseMYSB8DORNXuhXHtUn/G6HFgT071UsLdFSvyV/5WOn856ScPqj0DxtjtDZGOl58znhxDKwdAzkT15Wn/Ou3JyfltQOMMVobI05UjBHHwPpiIGfiSrfiuH4pabVn6fznpLx2sDFGa2PESYsx4hhYXwzkTFyUylXyvlGPVjrjpLx2sDFGa2PESYsx4hhYXwysi7isiftGv+akvHawMUZrY8RJizHiGFhfDDBxXQX7UlJmYQw4BjgGOAaufQxkI3MmrqsgLu7KCDACjAAjcO0RoBsBJq5rjytrZAQYAUaAEdggBJi4NghYVssIMAKMACOwMQgwcW0MrqyVEWAEGAFGYIMQYOLaIGBZLSPACDACjMDGIMDEtTG4slZGgBFgBBiBDUKAiWuDgGW1jAAjwAgwAhuDABPXxuDKWhkBRoARYAQ2CAEmrg0CltUyAowAI8AIbAwCTFwbgytrZQQYAUaAEdggBJi4NghYVssIMAKMACOwMQgwcW0MrqyVEWAEGAFGYIMQ2DTi+sd//EesVzbIZ1bLCDACjAAjsI0R2FTiWg9ORHL8jxFgBBgBRoARsCKwzYirFvl5O7DbobuRrkyvv5LzjdCp7MimO1ud6q+O62mr+lzpcbPGyjROpvIr9Yf6XYXO2nzk5eUhb8dupITi1Zhzrfo6dmPHqs/ItVK+Xj1XiHHO+F6h/vW6cd20v0Z4bYEY21LE5ff7cfPNN6O+vl5sK66Ol3TApytb3TN7iVWH9Tp77/XVZtOdrc46ynraWvuu93qzxso0Tqby9fqht79SndQvD/m1uq71nF/puOsZ40rbXmvbrkRfNnyt+qzXV+r39drPio/1evv6vWWIS5HW448/ji+//JKJa82Y2swg3KyxMo2TqXxNkLI0uFKdV9pPmXK1/ZWejThea9uuRF+2PtY66/VGYLKddVrxsV5vX9+2BHFZSYvgTP+MKx3wepkDu3fkyW0c/a5YLG1VeT5Sb5apv6rLQ564lTZ01tK2i6zboe9PZtVnBENKG/0OXbcXgNZux+7dabZCSV86v7LbWJtv9Yn0yD75+TuQl2fgoI1vlokhdd/T20VjJFceafxSlSljrO6TtEfXQedXMh+6/lR8aXtPmaSwkNOqj5UOa2NOBX5JXM2YSPEvGV+r58AYR8WbHmvmnqMVgx1I4mP1JzmWsnC1Xzuwe7extZmXB9PmVTGVzrbM4632zbBAwyJzPFv1qnlJtSFpK+lOrbs2n1MD67T4WG2UWOcc88kJIUU55CWFQUrHlIv0mBs+rIqfq8VLt0eOkYxDfUzjPAcMs8ZDiqdrX2wqcdEWIG0FElGpf+lIi+quiLhobzyZmYwhdJAp/vO1D6+ywtJGfUjUMwyx566ShKVtRn3axIsPs3o2p/en82Q7x24iFNVO2SZtTu+X9pwlxUatr0FWeoJOJgTdFh2bK7CLcNixw8SWfJHjpOqSRK18lHWr7ZEf9ORUynbmM6VVeCYxTKff1LOqH9lhGSttDGXCk8rJNuWPjmGmPpb21v4p15nwMXRnjD1lj4GbAkCPkbR+rmFbjuOp4TLGs/Ax25wp+3UM02Bt6DHjQvcvBcds86JujmSb5M2bBQvlu45bxpjX7ZbxlYxxVSfnRmGVGreqTaajbpt+Tu31a/1c1WXKGdQ225zoNz26XtnPzE+r5iCpM3M8ZPIzc/mmEhdtAdJWoCKvTKRF5l4RcRl3eylBYpSJh+kpd7o6KPpEUHmW61z0iTaK6OQ4yTs1TTe1U+Qomml1unnGmCl+ZbNRuJC8y06SoUV/Jl/WY5dhf23+DuymFaq4pg+rkXzEGDlgofm/Y4f+IRHOpJKDyDHGByKb/mx1Bn6rxhJ9rOPrk5EjhrnOQdZ5XMdYpol6H/3cgmNaPy3tjTZpPzsiQanVpzbXOcdzrjFhOpb9cymaafZns91UqbXPtT/pXSvmTf1q1Zbqq6gW9qWWmzkixXatTTrM1xM/2dpmsydbv2x1GlYSEiveOlDrO99U4iLTdPIiAlPPtKxmpycuLSGqDmkAl8yeObGprsmjFdAs12nGS+oxztK0MYNSn+h1TmyKX7oeMaxmc8r4OmZaG+qT0k7zIme7lO5a5JuElY9avX+aMdJiYfqQJ1Zu5h2cWa7fhdO4mefX1L/m2OnGkjikYq1hY8U9zRiidUq5wolqLHOQ9drSNkWnbpN+rvfRz9ONTSFAq3x1V2xpn2m8lHLNNyrfUsSlJX0dIvPc4q8+Fyk+mh2MbT+KxSwxn9KcttzT2JFGvxm3en91ntJew1y3WbTVfdLPqTLLdYp+OWjSniz91tKZSzwoH9dx3HTiItsUeWUiLWqTnrhop09b6hp33qlJTnpPH0i5QiHQs91BU/tsE2Otz1WfSgZWgtDHkrrUdoFMInqClr7o/6f6pbfV9NKdmQoYEZCqndZGKJXjp67klL9J+7PZJeyxbBHm5+vbsak+ppJlOnukrTTPSbssdqZ8yNbSn/Qj09ipYyXRTmKdLEsfK7qtRtuc50AjYQE9rZTXO1+Z7MuMr94j6We69uv1LYl35rhZa86U/7qVAhzLyjudvaqvHCMZQ1Zda+nL3H/tmNfHkvO72o5sGOj9jfOM8bTe+FH4WP3PZg/VZeuXrS6XeEjj7xpF3whxrWGTqM5EXNYHnWaCpl4pS2ntLkckOrWtoe1pa4YIQrS+DLDqgafRIQd9MkmqMTNNbKrNGR9epvUrWzDJYBZbPDvyka+27VYRtCJVZaeGjTZmRrsIjhRiTHNttlFjZMEixT7DB0HA0lf5cFjqUWQvZiRlPnT9yp61xtbG0vxOPu8w5l0crLhbx1AYZpoD4+bLjLXUGMjLz9eSRK5jZbLP2l+7zuBn6udg/b7pn8G142atedH9kuep9mn+pJublLhQ86LrvML+ucS8PoyIa+VrMpFnzhEpnY2LzPGkY54aP9ZYW4+/+ucoW79sdamxnTUe0rmcpWwbElcWb7iKEWAEGAFGYGsiIAhfW1BchZWbSly0ilqPWP1KeUisXrTQjtb2fM0IMAKMACOwNRAQq2X1COMqTdo04rpKO7k7I8AIMAKMwLZCQNveFAuMa7PaIgiYuLZVILCxjAAjwAgwAkxcHAOMACPACDAC2woBJq5tNV1sLCPACDACjAAT11oxYH31da32XM8IMAKMACOwoQgwcW0ovKycEWAEGAFG4FojwMR1rRFlfYwAI8AIMAIbisD2I66Ub8PT65XylUvzJ1XoFwHM7woY3+pe158nkX3S/4S/9ZcE1OudxjiZfto/pz9roHRt6HyzckaAEWAEtj0C24y4LD8vov7UgPhJFUr8VK8TAF1rv22Y8rwqmy7999n0dvq5/DkTSZjGOOp3iMTP6Sg7LMRqhkwmXWYDPmEEGAFGgBFIg8D2Iq6U1Zbx218pZKH9Dphw1kIOgmuMNhl1Wfto11fcR5GYNgMZdWlt+JQRYAQYAUZgFQLbkLjSkAC5ZfxoqOIx6alGOqJArn5EG0Ec6XRZ+2jX17JPRl2r5ogLGAFGgBFgBDQEthdxGb+ybD7PMh0hciESUkdVQdfatl8KWVjqVBehI9MvI19Jn2xbhZptGcc3K/iEEWAEGAFGYFv+5JMgn+SfCMjL3y3+qKAiM/E3gCwvZ+T25zDUnz0gcspEXNaXM3LsYxCu+pFgc1W4ypdaWjpaxuc4ZQQYAUaAEdAR2GYrLt30XM6ZBHJBidswAowAI7CdEGDi2k6zxbYyAowAI8AIXO+/Ds8rLo5xRoARYASuNwSu8xXX9TZd7A8jwAgwAowAExfHACPACDACjMC2QoCJa1tNFxvLCDACjAAjwMTFMcAIMAKMACOwrRBg4tpW08XGMgKMACPACDBxcQwwAowAI8AIbCsEmLi21XSxsYwAI8AIMAJMXBwDjAAjwAgwAtsKASaubTVdbCwjwAgwAowAExfHACPACDACjMC2QoCJa1tNFxvLCDACjAAjsInEtYj8/GnsnmfQkwjcyJhcI9/nw9jBcZUMKT5jBG4ABJi4vtFJvkbJO8WHjdCZMsAVXljtsl5foVruxggwAjccAkxc3+iUb0Ty3gid1wIkq13W62sxButgBBiBGwGBrUFcYrtnCHn5JC7Q3wGmf7WHVNkQ8g4tGqUy4eUfmjbaGgmw1mX0H8KO2q+MtvrBaDdKW0tSb/4o4KglPfI6pV+KTUOgtvKfdXwAKW2T9qsedMzmy27NpvXYkNx2NXybp2M6zHRLvsLuN5NtTL9SfND91fsmz7P6Y24HZ7PLqLtC31fNvxjT0JkpFjQfd9SGees6OZ18xghsKwS2AHGp5GbgNupKQzx6GzrXyUlem8Q2SgSWjjyMdm+G4aChRDtNT0o/2TY1qavnc+nGV3VSbwr5rAoH6q/aW2wSiTW1LrMNqh0NYNWp1+kGSNJabZ+0I/1Yev9059nGXqtuCHkp86HmLZs9si7pg3UM7SYny5zKG5ZMOKXzk8sYAUZgqyDwzROXdhesVj6pJKRWByrJ6ImKYFzrWkG9VjutXtikkqjsTysMmdi1dlSVzX41NB0NopQ+ZvJFrszEOOuxIQUDi326DWl0iuo05aa/Kf5pmOTkj26Lfk6jZrnOZk+2ftnqSKciSeG0dXwdKD5nBBiBrYzAFiEuLSEqtFKSF60UMiV7awKyXiuF1vIs1yljy/5mIrcmxzRt1YjmMaVNNl/kimhLEZfphHaSsz86xvo56cpynaJfjpsR/xQ9a+hk4tImkU8Zge2LwDdPXCLxaFt2Cku6o1eJRiSyTSQuw6bUrTNFrumSYxr7lR90zOqL1jclYdM4apWnVnbKBo3glP6U7UeFlW4Enct+yW02VZ9tLNVGO2b0Zz12pcNR2Z3NnrX6KR1kr942VSdvFWrzyaeMwDZDYJOJS237yaOZQEXC1urEixgyCYqttTddyN/MFRdNYopNmZKhMdspbbVnLGYwZPdFvmgg/TfJMqsNlq3HQy7tuZn2Ioj5QotpiJHMk1ib46X4oPur91XnmfxZj106qZBey3VGeyztUvplq0u1jV/OUHPJR0Zg+yGwicS1/cBhi69jBAQxqhXsdewnu8YIXIcIbBpxmS9e6K9r87n5Kj7jk1wFbjYW1+Hnml1iBK5rBDaNuK5rFNm5bYCAtr0pbph4tbUNJo1NZATSIsDElRYWLmQEGAFGgBHYqggwcW3VmWG7GAFGgBFgBNIiwMSVFhYuZAQYAUaAEdiqCDBxbdWZYbsYAUaAEWAE0iLAxJUWFi5kBBgBRoAR2KoIMHFt1ZlhuxgBRoARYATSIsDElRYWLmQEGAFGgBHYqggwcW3VmWG7GAFGgBFgBNIiwMSVFhYuZAQYAUaAEdiqCDBxbdWZYbsYAUaAEWAE0iLAxJUWFi5kBBgBRoAR2KoIMHFt1ZlhuxgBRoARYATSIsDElRYWLmQEGAFGgBHYqggwcW3VmWG7GAFGgBFgBNIiwMSVFhYuZAQYAUaAEdiqCDBxbdWZYbsYAUaAEWAE0iLAxJUWFi5kBBgBRoAR2KoIMHFt1ZlhuxgBRoARYATSIrBpxFWbn4f8Wt2GWuTn7cBuh1ZWm4880ShNndYst9NroWOtkbKM4diNHVb/1lJ3zeoz2ZWp/GoG3gidV2MP92UEGIHrHYFNIy6YpGRAKhJ7HnZozOXYvcO4vhbJ8FrosE6/Vaf12tr+m7rOZFem8quxcyN0Xo093JcRYASudwQ2j7iIqHbshlpgEUnl796NHeYyzIHdO9QK7Fokw2uhwzr9Vp3Wa2v7b+o6k12Zyq/Gzo3QeTX2cF9GgBG43hHYPOKCTkzqnJJePuQOovV8B3bX0nZbHvLyUldmMFZrVE5icl/KbBkJNYMO2rpU/eX2JHUmu5LlqXpJX7IuZUsz7RjG+IKps+kFUrdR9X5kkkbuGf2WffLzdyBP4KnroPO81C3YtPYaY2k+pvi/xthy4ayPlTIZ0o+0ug1bc7JJj5Ud2L0735xDfeWeHNnQnaldBp9ymg/aQdBuxJJj8hkjwAhsNAKbSFx6gq5FvvGhr803VlkpW4lGAlSJgepSCE4jK5F81EpNhyubDmu7dDbobdS5kQjVshHZxtDapvimdGlHvb42Hzt2qC1TyvfqXI5lkkmK37IumbzV2JIwzT5We9PoMNuuq47ws46l+WeMm023SQKrxtXmlrARDCn9NW84UuJj9bjp22XBM5f5oDYqPvUh+ZwRYAQ2HIFNJS7zOZeWGFRiVkfpsUq8yn/tWiQ2dedttF714geVa31EM8u1SHZqBWUkR6HbsrpTJqTTkXUMbby19FK9TuS0+hDXRAa6bZn81sbS7Nyxw+qLtZ12M5EN12x1Bgarx9KAy6G/9qgzuQIV/dQcGUfBflY/rNdqbGu5dp3NJqpbaz7UEHxkBBiBTUdgc4nLSAi19HxLvWFIZfm7kwlaQKAlGOt1toSTAl+uOjRyMPoTiabfgsyi02rnKlKTq6f0epUNaiVK1/mo1RKo3B5dD3HliZWbudpYZR8V0DjG6jUbrtnqhJ/pxjLAFMPQlm+utme3SWpdax7U2FnaZfUph/lQQ/CREWAENh2BzSUu8xmStv1jJL7kViBhkCXhGO1TiM+SFCWKWXTo2zwigen2yN6pK0A1L1l0iiZ6vX6u+utbf8kyOhPjWbYI8/PV1hi1IH3WLVJFBtaxktf0vCZ1C1G7Tknea+lfe+zUsXT/1tZt2pjGJrPOVJn0TxZZr1VDa7l+TeeZfMphPvQYUsPxkRFgBDYFgU0mLmPVYXk2QAkv+8pATzjWlwhWk45EztInhQzlXb14OWNHPvLVdlzK9qEihdR5ELZaX3ZIeeal7NHGz0GvXFGpvspH7ZrMEEldbZ3pddpYwlz92vBVYC7L5UscUo95A5BVf65j62Ol4raW7bnZpOJE94/GsV6rsa3lluuMeCp/NYxFW+2aiUuBzEdGYNMR2HTi2nQPecAtjoCFTLa4tWweI8AIfPMIbBpxma+ea69EZyr75mFhCzYPASauzcOaR2IErg8ENo24rg+42ItrjwAT17XHlDUyAtc3Akxc1/f8sneMACPACFx3CDBxXXdTyg4xAowAI3B9I7DhxBVZ/grBxcvwxC/BHrmI6dAFjAdWMOxdxoBnGb2uJXQ7l9DpWEK7fRGttkW0zC2ieW4RTbOLOL+GUBsh1F6XTOVaGxpDSQuNazCiPD8AACAASURBVJPjkw3CDsMWskfZpOzKxTar7Y2zizBlZhGNM4toMGUBDTNJqZ9ZQP20lLrpBVilNk0ZtRF9hB6p2xzPgqOJmwUnhQcdld/6MWO9gZ8VQ4WlflRYi6MVWzU/hl1WDNW1dc5X2aXsUX6o63RH1UaLB9In4mk9+CjdFp90XWS/nPfUuaX5rJ1aQI0m56YWIGRyAedYGIMNjgEVexSHIpfMLKBxdkF8DuizSvm5y7mEPvcShrxLGPcvYya0DPv8CtzRFfhjFxBKXEBk4QJiixeQWLqAheULWFq5iGWSCxexcuEiLljl4sV1s+yGE1dw4TI8sUuwzV/AZFASFpFVJ5HU3AKaZhfQMJ1A7VQC5ybjqJ6Io2o8jjNjUirG4qgYjaPcIqKc6ox2qv16j5VjcVSOyzGrxxNifLKhelwK2aKE2ir95vij0j6ycZUYtlvtLxuNQ8hIHGUjcZQKiaF0RErJSAxChmMoNqRoOAYhQzEUWUXVGW1LhmV/0muOpeEn7DSwM/3QfFOYKFyU/3SksnSit1HYVU8QnhbR8FR9hD5tfNMmzeZ086/mQh11u5Tu9RzN/uls0crMdml80cdL5xf5UabmWc3tUAyFQzGcJhmMoUCTU4MxsDAGmxEDFHcUfxSLlGso91CsVozFRA6k/Fw/nUDTbAIdtgX0Ohcw4lnEpH8Rc8ElOOeX4I0uIxBbRji+jEhiGbGFZSQWV7CwtILFpRUsLUtZXl6BKSsrW4+4FGlN+Jcx6FlEp30BzbMJ1E3FcXYihjOjBE4UxUNRnB6M4FR/BCf6IjjeF8Gx3giO9s7jSG/EkOT5UVFH9bLdMWpv9KF+GUW1M440DsnJ/uyibEraJcdWdigb1bX1KOp7IjjcM2/KoZ55COmex6HueRzU5ED3PA50zWN/1zz2kXTO4wtTwtp5spzaUFvqQ/1JnzmGOa7E0mofXQvMDDwULidoPpRY6qgN4SLEaLMWjqo+nU4530lcj9Dcm3YncTvSk/RB2Uxzr2w+ruxd71HTQfqsGKkYU+Nk8l34ZtGlfCN/aK5pfsTcijkNY29HGJ8b8ll7GCSfavJJexgsjMFGxYCKNYo7isMvOsMiPimH0OfwRN88Tg9EUDIcQeVYFLWTMTTPxNBlj2PQlcC4N4EZ/wIcoQW45xfgjywiGF3EfHwR0cQiYolFxBcWkVhYxMLikpDFxSUoeevdPVCSC4tt+IqLtgdppaVIq3EmIQirfIRWDlFBGJQgKMHSB3lvx7z40H7SFsbHhuxpDWN3axh0NEWrp3ZiQuloiOor6rRyVW8e2+fxafs8Pu+QQuMrUWV0/Mxop8ZR+ve0hWEK2addm20Mu8kHko9IWsL40CIfNIdB8n5zSMh7TSH82ZA/nQ/hXUPeOR+CLqqcjn8y2r8ndITxgWUMGnsVlobdJlaGr4QL+S1Ew4DKrfIZ1RsY6rh93pnEVi9X7aUeOW8mXoRhBqwIN4UjYa36fGKxSenP9aj7o8+xms9045jYEEaa72LMNPFCusj2D1vk/NLc0ry+0xjCHxuDeLsxiD80SHmrPgiSN1kYg02KAYo3ij+Kw3fOB0Uu+aA5hN2tIXETta8zLG66Tw1EUDocwdnxKJos5DUbSAjy8gjyWkAotiDJK76IeMIgLkFeqQSmyIrIK5d/G05c9EyLnmd1ORZwfiaBqnFJWHTXSmxOJEEkQgmJEjUl37cbkh/aN+qDeKMuiNcNoXMhYjJDeLM+hLdIGoyjuE72N+vrtbaqj9Hv7QZKHDKBKEIgO2RCkXVU/4cGKTSeSijKPtMuZV9dMuno9r9WGwTJ7w15tTaIV2uk/K4mCJLfngvgFUN+czaAl88G8FJ1AC8a8kJVACmi1VE7av+bcwH89pzURzrVGDQuja/wVEeyUfqUxJP8JWyENMqjwsB6fFsk3yRWVjwJSyVUR+1Jr9KjkrTCkexKwYl8MDBT9gvs9TjQ9An9ahztSGNbRflo2tKgza+aT2McijPVTvVL53uqb1If+Ua2/65Gzq+a1xeq/Hi+0o9nK/145oyUp8/48VRFUp6s8IOFMdioGKBYo5ij+KM4pJh86SzlkABeqw0IQvvT+aAgsb2dYbETVjSUJK9uexxDrjgmvAnMBRJwhhLwzicQiCwgHFtAJL6AWGIB8cSCXHUReRlCq67l5WXBV1uGuOhFjD7XElrmEjg3ERdbgrTCom0vuoul1QUlNEpc4kN9LgBK1pSAKTk/XxXAc5WGqHOjXCVvldBTjlpyF+XGtTpXbV+qDuLls0G8co4IY7VQOclvzlK7JIGoscm+TKK3IR+eNeSZyoAIEAoUIUaCUkH5RLkfj5f78ViZH4+W+fBIqQ8Pl/qQX+LDQ4Y8WOKDElVG9dSO2j9aJnU8oSU8GZw0trTFxLUy6QPZLLEJ4iXhs8SHMCKhYKa5EUc619r8hnAy8FK4EabqXB1FO7Ofgallrgkr+hBZE7j8cBn2a9i/YJA32aPbpOymI82hstE8mnYY/mk3B9Z5Vdjo+oVOQ7fpn8KKcCJ9RuwR3uTTkzS/xrzSnD1Y7MMDRV7cV+TFrkIv7i304p7TUu4+7YWQAi/uYmEMNigG7i6Q8UaxR3H4QLFX5JLHy33iM/hCtV/ccL3VEMT7zUF81hES5EUrr9qJKFpnY+h1xDDqjmPaF4c9kIA7nIB/PoFQdAHzsQVEDfJKCPJaMIlrYXFx6xHXiI9WW4tomKaXF2LieQk9h6EtE9oqoaUpERatMOgD/qxxp0nJWyZuPx4pXS2UmKmehJI8tVcJn64f1+upjdZWP3+iPIAnKwJ4+kwARCiKXMSRygyh+qcqAjLpaPrJjkyi7KN68uFhkhJ/KgEVG4mr2If7i6TcV+TDrkIf7jWSFyWsO095cccpL3590oPbM8ivjTZ3Fshkd2+hD6RL6X2gSI5FRJdv2EL2kF1kn8JU4Feu7m4lPsJ38r/CwNokRFlPGD51RuJIWAk8DUwlUafBUtMn5tqwQ+IkSVokdZHYfXiAjoQX2V9ixISB/2MG2T8hdKbarGxX9tHRFK09+aBiSNhjzJsVGzUG6VVi+ku+G+VEUEKfEXuk5yFjnmluaV7vOOXBbSc9+NUJD2497sEtxzz4BclRN35+1I2fkRxx46csjMEGxgDFGMXbL465cctxGY+/PuURN1BEYnQD/cwZn1hUvFkfwAfNQfEcrGBgHpWjETRORdFli2HQGcOEN445fxzOYBzecByBSALhaAKRWAKxeEKuuiwrry234hr0LIvXKGsmYygZjuJwb0Q8j6JtQSIt2rqilQzdjdKKgBLGw7SqMJIUJV1Kvla5v9iPBwx5sNiPh0ooKfhB55TszIRnnlN7WU5t5LnsR0n80bIAHisL4PFyTYwyKn/UIB5KmDSW1OHH/Rrh3F/khxRJFtI+CxkRIRX6cM9pH+4+7TPvIIlsiJgkOXlx20kvfnXCi19qyeznRz0pSewnR9wgUUntZ0c9oDb/fUwmQep/+0kiOy9SSY1IUZNCSZSK5Mhu8o98JRFEUpq8FlgbddY2j1iI/LFyiSvhqwhekTjhTv3likPOsSBsQdo+0F2gTtqEDeF0V4HEj9qquKB4eNCYG2GTulGwHMk+IRpJCjsMW5Jzm9StxhC4qDEMveSLEOGf9NH0T4tJimOyl3yi+SCiIpKiZEFz+KPDbvzgkBs3H3Tjewdc+C+S/S58d78L/8nCGGxQDPzHfhdIKMYo3ij2KAYpHumm6dbjbhCB0Urs4RKvWH29cs4vnoN93EarrjBKh+dRNxFF22wU/Y4YxtwxzPhicARi8ITi8M/HEYrEMR9LICqIK4FEgoS2DeXKa8sRV797Wbz2Xj0eQ+FgVLxNRast2h6k5xj0LIa2ZBRpUdJRH3KV4O+iBG8kekr2JJT47xEk4MeuQj/uK6KjJAXqR4lZtMlwVDruNfpSUkqXkFWZSVRFftxX6Bfko+xTuqzj6XbcXeDDnYbccconiIRIhcQkqRNe3HrcKxIakY8kKg9+ctiNHx5y4wcHZWL7/gEZYBRkSqjs+wdlG2r748MeEJHR3TvpoiRJd1K/PCEJ0SQ0K6kVJPEVxKCRw30GwQm/jHNqI9op0tZuKFSiJ+wUflSmbkbUfAkSN1aVRLCU2AUuJzyCuNVKhOyncyJkwkwSmcRVzIEx/7tojtKIuKmg8XUR7XzYpVa52k2Fmi91pDEoXki/fuMk/NTiR/hqjE+xSbFIfe885cPtJ+T8/uyIBz8mshJE5RaJ49/3ufCdL1z4t70ufGuvE//6uRP/QvKZEztZGIMNjgGKN4o7ikEisu8dpDwiV2G0y0Pb2LTyer7Kj9fr5KrrYHcYRYPzODceQctMFL32KEZcMUx5Y7AFYnCHYoK4gkRc0Tiisbix6jKIK0HEtbD1tgrpy2rNswuoGouhYCAiXtf+oEU+4KYXBugZAG3H0ZYK3dlTEqCEJpKZWJH4cEeBFJVA6HjXab9IBnef9uOe00QkdJQJgpIEEQXdmVOyEP1O+UCEQdd0VEJ1pIMSjFoxqURERyVUR4RF7e4pVGNLQqVxpPjl0bCb9JItwg7yQRCWD7ef9KWQFZGJJCyvIJkkYXnwI4OwvnfALe6I/nOfC/+xzwVKcv/+hRQKNHG+zwWqpzun7x+Qd/B050TBR+T30yMGmR2VRHarsTIzyUBboREpyGcqEssUTDUSVnOibizkzUTyBkKRkyI7lcQVkYsV5ikvbhOrS4WDsWUmVpgeYTfZLuw/olaVXpOEicRupzk17DJt0W5yyH5lGx31mwxxY6TiRc2TcUNBum876TP1S90yBigWiMQUUSpClDdRMi4pBggjmnvSc+sxL4i0aF5pjmhFpciKEgcR1D9/6sQ/ferETZ848X8+ceJ/f8zCGGxMDPzjx06QEL4UbxR3Oz+jGyeZY7530IUfH5Hbh3cWeMQ2/dNnfOJ515+bgtjXGcLpgXlUj0XQNB1Bty2KYVcUk54o5vxRuIIx+MIxBOdjCEfjiAjiiiMe3+LERV82pi8Z07v/9Brl3s558UIGPeSjt93oRQAiLnqukom4VHKkoyIISQpJ0iLiUquslCSbQlZqK84nt89OyoRCOsWdtLH6UgRmPYpEJVZbyaREdhCJSiIlokoKERyRqmhjkO+vU8jLJ1YPckvQi1uOE3F58QsjYf/ksExwtHQnMiJSIoL6zhdOfHuvE/9myLc+T55/+wunaCMI7IBcodFdPYlcicmtRSJHGkcJrciIwGhrUqxoTiS3F8XKRm1jGisisf1orIzIJ3EjoBGHmCftRkLOm5w/0kciV1VyBUhjq1Xmz4lgaQuUSPeQtPuHhv2U8ImEKfnTavKWY5LsiPxJHxGYsCcduVL8aDcSKq7UTYycm6RdpFOKD78yycuYa+MG5t7CAEh2FQVwnyEUJxRPct79Ahu6WfnlCZ+YX5rXmw968N39bjFXtML6l89d2PGZTByKrCih/MMeJ/6XIX+/xwkWxmAjYoBi7B8UgRF5UU4xVl60hU35glZd9GjkyQqfeCfh3fP0nCuEU/1hVI7O4/xUBF1zEQw5o5gg4vJF4QxG4Q3HECDiisRSiCtubBduyRWXJK5EzsRF2yz0TEFsw2kffis5ECEQMQjCMlZCaqUmt56MlQ49FzHkDmN7SSVdOlLSoqRKuijh0KrKSlgPFAdEmdp+UomJxparL3kURGWU6bapNncV0N138g7815QMta1Cseoi8jKJyy3uzK3EZSUtscSnZb5BYERstCKju3naSqRtxJsPuPCDg64U8iJyEA9lj7jFywCCvI4p8pKBqrASKyODqARBWM4VeSkyUEfCVp2LIxFfCmlJwlSkpQiLyOnHh1z44UEXfmDYfzOdH3QJTKhekK+xFXorbYEaWN5ujKEI8g56fkhbkcKW5Isuqp58VD6JFZaxnSpWwoK8FHH5cUdBkrgEaRVJ0iLiul/EibymurtPB0BzfscpP24/6RfE9YtjXvz4sNckru984ca39rqx83MX/vkzF276xIX//YlL3AVTIqGEohLV/7vHCRbGYCNigGKMbpLoZummT+kmyoVvfUHPv9y4+RA976KXiOiNQx/oTWV6xEPEtTcTcbmjmCXiCkThDUURCBvEFY2J7cJ4PI5tRVz0GrzcKgzi9zXyxQx6g4/eVqOH9/SMi7bnxHZLkdoClCsXnQzU6sfcphFbecbbeMYzLvFwn7a8DEkhMCItg8gouRJR0jMcmhgiLrVFSMcHiwPaMxqVoJI2UtLS77jVnbdIZMXyTlyRnVqB0d04JVJ5t5+8y6fVDm3hyVWXXF3QaoPIR666aEXlxHf2qlWXA//2eVK+vdchVmT/sc8piEuRliKuHx1yCUIQpHXYhZ8TaR1x47+PunHLMTduPebGL4+78avjirg84k1GkeRP0rnxsodxpISffPFDrYiTR7lVqrYdk6Qh3o484RHjiBdQ6C06g0hppfWTw9JOSVxOQby6D5K4iHDltiLpEFuGuj3qLUvtSC93qDc00xGXupGgrUuxEj6xmrTuoVWWWmEVB3G/IQ+UBEFC1xQD1Iba3nU6gF+f8uO2k37cctyHnx7x4geHvPivAx6RGL79hRv/qpPXpy78H0Vgn7jwDx9L+V8fu8DCGGxEDFCM0Q0Txd0/febCv+x14dv73PjuATd+eJh2N+TnXKy4zvjx2xpJXPQLG6fEm4WWFZc7gllfRCOuKEKRKOZ14hLbhYmt+4yLvsNVPS5/0ol+HeOjVvndLXo5g16Dp+/H0Pdb6DkXvb0n3zST5EEkolY6+koolVjkw/8Hi3ygV77Fw396aeC0F/cWSLmHXhE/5RVvddFRkZn6/gKRFvVVr4yLN9OMN+vk69nqrboA8ksCeMiQB0sC0EWVP1QSRH6pFCqjNnLlRkQmfRIrNuPlEflqtCSF2+ilBFpJGMmckjglcErc39vvxHf3OfEfX5A48O9EVJrQNZVTm+/vd+IHB534oSE/OujCTw658NPDLvziiJT/PuLCLUdduPWoC7885sKvjrtx23E3bj/hxh0n3bjzlEfIXac8UKLK1I2AeP1evIIvnx2pLVta+erfSRLfTSqQekjHHfRa/wk53i+PEXlKm35+xIWfHXbhp4ec+LGy/4D040cHncKHnx1xmWQrSOuEIliyl4jSY8rdxjkdlQhfdFvIHoPg6CheEhFH49kZbfkqwiKiKgniwZIgHiqVkl8awsNlIeSXhUQZ1RGJ3VccFFuJtPq6oyCAX5304xfHfPjJEZ8gr+8d9OA/93vwnX0e/JsisL1u7PjcjX/+zI1/MuSmz9xgYQyueQx86sZNhlC87fzcjX/9wi1I6z8PeHDzIQ9+etSLX56U7w/QG7j09Rb6MQD6dZ79XeHkM66pCLrVVqFJXBFjxaUTVwxixbWViWvAvYTWuYT4eRD6pjX9Thu9RknfwqYvHb9aE8DL1fQ6vB9PG98RopWX9ZVietVdkIl6RVv7/pH5SrL4fo8P+cU+PERfoiv04v5Cj5TTHtxnyK7THtxbIIXI7f5CLx4s8iKfvnRX7MUjJT48Sl/iFWJ8V8z8Xph8vVu8Im+8Av2I+Sp0EI+VJ+XxiiAeN64fLQvikbIgHi4NCBHkZ7yWT2RJxCm+t0Wve5+SSZgIRCV0SuREOkRCNx8gUnLge/sd+K99JHZ89ws7vivOHaLu5gMOyCTvFARAJPCzw0784ogT/33EiVuPOvFLkmNO/OqYE7cdd+H24y78+oQLd5xw4c6Tbtx9yo17Cty4t8CNXQUeIfcSdiniFXbfR1gbNw3qBuB+moMiiS9hTHJfoQcSfzfuOeXGXSeJIOXYvzrmwq3HiEiduOWIE7847MDPDjvw00NJoeufkw9EtMddSZIlYi3w4B4Swz4axyoUA7tOuw1Rthj9VH8iYYOI5UsdfrF6ohW0IisiqEfKQ3jUkMcqQni8IozHKsKijOqIyB4qDeGBkpAksKIg7jwdwG2n/LjlhB8/O+bDj4nADvvwfVqBHfTiPw948e/7vfjOfg++TWSmybf2ecDCGFzTGPjCg299QTdNMt7+fb9HxOD3DnnxwyNe/IyeIZ/04c7Tftxf4sfjFQG8eDaINxtC4qfr6LdXi4fUW4UR9NjorULj5QxfBC5zq1ASV0SsuLYBcQ16ltBuS4hvV9O3rOlHcz9vD4kvsL3TEMAbtQH87pwfL1cbP3sjvoDswxPlJPIXBh4r9eGxMhL5RWL6AjHVkdCXPE0p84lfJHic2pd48UixBw8XSckv8uAhJYUePFjoxoOFsiy/2INHS7x4rNSLx0u9eKLMiyfLfHiqnEQS6jMVfgixfClZfDH5TBBPk1QG8UxlyJRnq0J41rh++kwIT50J4skKKfQlVvrOmPzirc/87hoRKCV4IgoiDiIQIhRK6rQyIuJRyfwnhxz48UE7fnQgKXRN5dSGEv8tRxy45ajDICoHfnXMgduOOfDr407cQXLCiTtPOHHXCSfuPunEPaecuPeUE7sKXLj/tAsPFLoEVg8VuiFEYVjkwYOGPESEXyJ/sUP8aofx6x2PlHrxaCndCEh5mOajmDAn7N14oNCN+067xFj3nHIJO8gesu324w7cdtSBX5LtR+y4RQj5IX243bD9rpMugdO9p924r9CN+w29D9IYhojxitxiXDp/yPBJxoC044FCD1KE5oFW4Or7YXTDURYUpPR4RQhPnAnjycownqoM42mSqnk8Y8jTlfOi/MkzYTx+RpIZEdlDZSHcXxLCPYrACgK49aQf/33Cj58f9+Onx/z48VE/fnTUhx8SoR3x4WaSw1K+TwTHwhhsQAxQjFG8Udz95JgfPzvuxy0n/bitwI+7iwJ4oDSAxyqCeL46iFfrQni3KSx+n5N+0Lp8JIL6ySjaxfe4ohhzRzHtjcLuj8IdjBpvFUblyxnRGGIxeqswbn6Xa0u+nDHsXUKXPYGGqSgqRiI42TeP/Z0hfNwaxPvnA/ijIC8/Xj3nxytn/Xipyo8XKn147oyUZyt8eKbCh6eNI50/e0aKaqMfZXsvni734qkyD54odeOJEimPl7ih5LFiN4RQXalbtH26zINnyj14tsKL5yq8eP6MFy+c8eFF+t0uJdVyhSh+9kj8PBC9GUmv9dNPDYWEvHw2hJfPhZNilL9YHcILQoJ4vioovnRNvxRChEgk+QQRLyX7Elr5eQRRPECrgwIXKLFTkqbELpL6MQd+JRK73UzslOBJfnnUbpCTA3eccOBOQ+464cDdJx2456QDu045cJ8h9xc48IAhD5524KHTDuQXOvFIkROPFpO48FgJSRK/x0s8eLxUiiB6QfI+PGXM1VOEvxAPnixLCmH9OOkqduGRYhceLnLioUInHjztBNlBdt0rbLTj7hN23HXcjjuP23DHcbuQO4/bcdcJu/ShwIn7TzvxYKFLkNLDxW48UuzGoyUk0mbTdvLBFOmTqCt24VHqY/ajmxiPIFxacYubJfp1FXFjEsKzVWE8Vx3G82fn8eI5kgheqpHyck0EJHRN5S+ci+D5sxE8Vy1J7amqeUFkj5SHTRK7tziIu4nICoO4ozCI208HcVtBEL8qCOCXp6TceioAFsZgI2LgllMBkJBuirfbCgL49ekg7iwKgmLzgdIgHqkI4anKEF44G8ardWH8sWkeu9sjONgTQeFQVDwGoh/b7bbFMOSiX86IYdavvoAs3ygMRWLm862YhbS2JHGN+ZbQ60ygeTqKs+MRFA/O41hPCPs6gvikJYAPmwL4U4Mfb9f78WatH6/XEIn58LuzPvz2rA+vVPvwG03omuS3JEYbOor2Rt0rVV78ptKDl8648WKFGy9UuPBCuQvPa/JcuQskVPZChVu0fbnSjd9UuvFKlQe/rfbid9VevHrWh9+f8+G1Gr+Q12vlKpFWiq/Tj9WaP1pLX6gO4436pLzZMA8SKnudpC6M1+rC+H1tSIj4Qd2zAbxS7cfLVT68VOnDi5U+QZjPlnvwdJkbT4pET4mVkrxLJPkHTjtEkifi2XXKjntP2lKEyu4vsAsyIhJ66LQd+YKM7Hi40I5HCu14tMiOxwrteKzIjscNeaLYDpIni+14qsSBZ0odeLbMKURh9XyFG1I8eL7Cg+fPePBCpRcvVfmEDy8bc/VylRdCxDx48OIZEjkXhPlz5VLv06VOMdYTxQ48XuTAo0UOYd/DhTbkn7bhoQIbHtSErvNPSz8eK3Lg8RInnix14akyF54pd+FZQ+T8OvFsuVOM9VyZE0qeLdP8KtP7uPFcuRvPVXjw3Bmv+OFb+fuEQbx8LoRXasL4Xd08Xq2P4PcNEbzeEMUbjVLePB+DKY0xvNEYw+uNMbzWEMPvG6L4XX0Uv62L4uVaSWjPnY3g6ep5PElkVjmPx87M45GKMB6uCCOfiM2QB8vCIHmAhTHY4Bh4qEzGHsXhY7SjUDWPZ8+G8WLNvIj7NxsjeLc5gj0dUezvieLkYEz8fcL66Tja5+Lod8Yx6lG/VRiHK0Tf4YqDvnyc8h0u8Rq8fCmDSGtxK/5W4VRgCYPuBXTMxdAwGUHlyDyKBsI43hPEwY4A9rYF8EmLHx81+fHBeT/+3OjHuw0+vFPvwx9J6nz4gyFv1/mghMqFGG3eMa5Ffa0Xf6jx4M1zbrxx1oXXq6W8Vu2Ckt9XuUDyWpWso3ZvnZPyhxo3/ljrwR/rvHinzos/Nfjw5wY/3mv0i1UirRTfbwoaEhK/av+++HMk9MYkSQQftiblg9aIKHu/ZR7vNZPQ7zSGxZ+0eLchiD/WB/B2nR9v1RJ5+/DGOS9eO+vFq9Ue/NYgUyJhIuDnjYRPpPJ0iQNPlRDR2PCEIXROZU+X2PFMqR3PlSXl+TI7SF4os+FFJeU2vGTIy+U2vFxhw28q7HjljB2/rXTgVZIqB35f5ZTYnXXjdSEevH5Oyhs1XrxV68Nb2lz9C5vI8wAAIABJREFUga5rvXhLzIMHb9BcnKO+NAdOoY/00hivnHGIMV8qt+PFcmnf86U2PFc6h2dL5vCMJnT9XKlN+EFtX6a+lU78tsqFV6uVOPFqlRJpP40l/SCf7NIv4Zts9/tqF6S48dpZ8suHN2g+6oLiLw+83TiPd5oi+FNzFH9ujeL9thg+aIvjw/Y4PmpP4KOOBHYbQuckH7Yn8EF7Au+3JfBeWwJ/ao3jnZY43m6KC5ITxNYYw6sNMUFsr9RH8Zs6KS/XRvGSJi/WRsHCGFzzGKDdAUNeqo2IG6tX6qL4XUMUrzVG8eb5KP7YHMN7rTHs7ojh8+4YDvXFcWoojvKxBOqmE2izJcTiZMSTwJQvAVswARf9Orz2O4Xzsbj4uSf6rUL6uSciLCmLW5O45kJLGPcuoM8RE3ugDRMRVI2EUToQwuneIE50B3CkK4CDHX7sb/fjizY/Pm/14bMWHz5t8eGTZh8+NoTOlXzaLOupjSmqvsmLj897sLvRjY8aXPiwXsoH9S5IceL9uqR8UO8U7XY3uECyp9GNT8578EmTB582e/F5iw97W6Vt+9oD2N8RNCQktj33d4bFH3080E1/qoWW0FEcIuk1jj1RUXawm37yKor9XRHspz8g2BHG3vYQPm8N4tOWAD5uDmBPsx+7m3z4sNGL9xs8+HOdB3+qc+OdWjfernHhD+dcePOsE29UO/B6tQOvVdnx+0obXjWEzl+rsuH1KjveqLbjTU3eqrbjrWqbkD9U2/CH6jm8fdaGt8/ScQ5/NOSdsza8c86GP9XY8edaO96rdUi86p34gPBscOPDRo+Qjxq9wl6y++Nmv7gJoRsRmrM9TV7sEfPgwUc0F41ufNjgwvv1TrxX58Cfax1ijHdr7HjnnB1vn7XjD2fJvjm8WTWHN6rm8HolySxeq5w1zmU5+fGHs3b8scaBd2ud+FOdE+/VuwyR+mkMsl0K+SHlz+SX8M2B96ifELLLhfcb3PigwYMPz/uwm+ajNQT6W1+fdUawtyuGfT1xHOhN4GDfAg71L+DwwCKOkAwu4ujgkilHBpdwZGAJhweWcGhgCQf7F3GgbxH7ehext2cRn3Uv4JPuBXzctYA9nQv4qHMBHxLZdSTwQUcC7xPhGfJeewIsjMFGxMCf2xIgoRsrije60aIY3N2ZwMddCXzWncAXFO/9Czg6sIBTwwsoGVtA1eQCGmYWxe/Q9rkWMOJdwJR/AXPBBbjCC/CKv8dFvwyfkL8Mr//AriKtRUlaW3LF5QwvY9q/IH6/in7Hqm0mgsaJMM6NhFA5GEDZQADFfX6c7vXjVI8fJ7r9ON7lw7FOH46SdHhxWJMjHT4c6fSBjqLebEdtZfsj1L7Ng4OtLhxodmJ/sxP7mpzYR0dx7sAXTUnZ1+QQbQ40O0BysMWFw20kbhxt9+BYp1fYRLad7AngVE8ABb1BFPSFUNAXRkG/fCW0cDAi/jhm8ZD8s9clw3GQFAuhv0MmhX6zkf6aaEH/PE72hnCiJ4hjXQEc7QzgSKcfhzp8ONDmxf5WD75oduPzZjc+a3Lj0/MufNzoxJ4GJz6qd+DDejs+qLPh/do5vFeTlPdrbaL8wzobPqpPyu56G3bXzRkyi911s9hjkY/rZ0HyScMcPm204bNGGz4/b8degZcT+1pc2N/ixv5WNw60eoQcbPfhcIdf2E72C+mgMi8OtdM8UFs3DlDfZqfAfm+TXegl/Z802PBxgw176uewu34OH9XN4sPaWXxYM4MPambwviZ0/UHtLD6qm8Oeehs+brTj0/MOfN7kxN5mQ5ocUPo/P0/22/A5+WHIZw1z+KzBuCbfzlN7J75odmGf8M2DA+1+HOoM4kh3WPxl7ZMDMRQMxlE4nEDRyCJKxhZROr6EsvFllE+QrKBiMinlkyuirGxiBSSl4ysoGV9B0dgKCkeXUTCyjFMjyzgxvIzjw8s4NrSEo4YI0htcwmEWxmCDY4BuqpTQTRbFHsXh8aElnBxewqmRJRSOLolYr5hYQvXUEupml9BsW0KncwkDniWM+pZAO2u20CKc4UV4I4sIRBdS/5xJXP0tLmOlpZHWliQuT2QZtuACJjwxDDuj6J2bR/t0GE0TQdSPBFAz7Ef1kB9nBnyo6PehrN+H0j4vSnq9KCbp8aCox4NCQ4p6vJDiQXGPakPtlHhQ1O1BYZcbBZ1OnGx34GSbHScscrzVhmOtNtCRhOqpHcmpdgdOdzpR2OVCUbdb2FDa60VZnw/l/X5UDARwZjCAM0NBVA6HUDkcRtUo/V4XPceLib87VjMRR82kJhNxUX5uPCbaUNuqkXmcGQqjfDCI0r4ASvokiRf1+HC624tTnR6c6HDjeLsbx9pdONLmxOFWJw61EMHasb/Jhn3n5/BF4yz2Ns5gb8OMONI1le9v0mUWB5pmsf/8jJAD56exv3EadDxARyXnp3GQpGkGh5tncaRlFkdb5iRWhGG7Eyc7XDjVSeJGQZdH2FrU60Nxr1/chBT30blPzNvpbpoH2f5khxMn2u041iaxP9IyJ8Y41DyLg02zOGDYtq9xGl80kExhb/0UPjeEzkmobl/jjPDnYPMcDrfacLSN9Cqx4WjrnLCb7BdCvgiZwWHyrUleK9+o7/F2h/SP/OrxoagviJLBMMqHIzgzGkfVRAJnJxdRM72E2pll1M+uoGHuAhptJBdx3p4qjfZLaLRfRINNSr3tIurmLqJm9iLOzV7A2ZkLqJ65gKrpC6gkmbqAM4ZUTF2AkvLJC/hGZOoCylmubwzoBssQdeN1ZmoFldMrIjbPzqyg1ojz87YVtDhW0OlaQa9nBUO+FUwEVjATXIY9vAzX/BK8kSUEYksIxRbFSisSX0QssWj8AUnj1+AtpLW0tAX/kKQ/ugRnaAEz3hgm3BEM2efROxtC51QAreN+NI360DDiQ92wF7VDXpwb9ODsoAfVAyRuVPW7Udnnwpk+lzhW0nW/LKe6tELte52o6LajtHMOJR2pUtwxh+L2WRQZQufFHbMoIWmfFX3Ku2yiP+mp6nOhut8t7KoZ8qJ22Ie6ET/qRgOoHwuiYTyExgn65ngUzdMxtMzE0TpLkrBIXNRRm6apKM5PzKNhLIS6kSBqhvw4SzLoQ9WAF5V9HlT0ulDW7URptxMlXU4UdTlQ2GnH6XYbTrXN4WTbLE60zuBY8zSONk/haJMUuj7eMiPqqP5E67SUlmmcaJnCieZJIcebJnCczuloyInmCZCcbJnCqdYpFLRN43TbDAoFRnMo6bKjrNuBsh4nyntcKO914Uy/R9hcPeiDEuFDvxtnel0op/ZC7CjpnENRxywK22dwum0aBa3TONU6LcY70Twl7DnWNIGj50nGcaRxHIcNoXMSqjvWNCl8OdU6g4L2WRR2zKFI6E7Vf7p1CiQFSlomcap5EqdaqCzpWxHFRKcNJV1kqwsV/V5UDQVwbjQs/mRDw1Rc/OZmi20JbfZldDjpA3wBXe6L6PZcQg+J93Ja6fZeRrfnMro8l9HpuYwO92W0uy6hzXUJrSTOS2gxpNl5Cc0OKU2OS2BhDDYyBs47LoKkyZBmx0VQDFI8Uny2uy6i04jxXu9F9HsvYth/EWOBi5gKXcDc/AU45lfgiS7DF11GMLaEcHwJ8/ElmKS1sIj4wqL5l49phZWUJWxJ4iJHPOGEeKd/xhPBuDOMIVsQfTN+dE340DHuReuYB82jHjSNuHF+2I3GYRcahlyoH3KibtCB2oGk1A1QmRPqWD/owmqhegdq+mw42zOL6m4pVd2zENI1g8rOaZzRhK6VVHXNiH7neueEDtJVP+gUNp0fcaNp1IPmMS9axv1onQigbTIoVpGds/TN8Sh67HH0kjgS6DOEzoXY4+ixxUS7zpl5tE+FhI7mUSJxP86P+tA47EX9kBu1Ay6c63PirBAHqnrtqOyx4Uz3HMq7ZlHWOYPSjmkUt02iSJPi9imUtE+JOqov7aBzQ9onUdI2IaS4dRzFbeMooaMhdF5CZW0TKOuYRHnHFCoIJ8KMcOy14VyfAzX9DtQMOIWNdUMeNAx70TjiE/afH/GicdiD+iGXmKeaPjvO9dlxtteG6p5ZoYt0ku6y9kmUkk3tEyhum0Bx6wSKWsZQ2DKG080koyhoMqR5VFyfbhlDkbB9QvhV3jmDiu4ZnFHSNYUKYfsEytoNIX/axoWUtoyhtJXOJ1DeTm2T/lX12HC2z4Fa8mk0gObJMNpmoui0xdHtWBB/zbvfs4JB3wXxAR4JXMJo8DJGg19iLGSVrzAWkjIa+gqjoS8xEvwSw8EvMRSQMhj4EiQDfin9/i+RSfr8X+JaSaYxuDwz/tcjNn2+y1DS778MEopFikkZo5cxEryMsdBljIcuYzJ0CTPzlzAXuQRH9BLcsYvwxi4gEF9BKL6CcGIZkYVlRBeW5EprYQmJxSVJWouLoL92rEiLCEvJlvt7XMS+9Oeb6RvUNu88pl1hjNuDGJ71oX/Kg55JN7rG3egYc6F91InWEQdaSIbtaB6yo2nQhvMDc2g05DxdD9pEedOgbEPtmoeoT1KojPo19M6gXsg06nqnUddDMoWa7knUdE3iXOcEznVNoEZJ54Soozb1vdNo6JsVesgOsql1xIn2URc6xt3onPCia8qH7umAWEX22+Yx6IhiyBnDiCuOEXcCoxYR5a4YhhxRDNoj6J8Lo3cmiO5JP7om/eg0yLxtzIOWEReahpw4TzLoQOOgHfX9NtT1zaGmdxbnemZwtnsKVZ2TqOqcQKUhVV2TqO6eEkL1SZlEddcEqjsnUNU5jqqOceM4hsqOMVSRUHnnuGhztnsS57qnUEOYEYZ9s2gk/IccaB52CmkZdokbj/ZxLzomfMJ+6YMHbaNutAw7QfNEc0Zz2NA3g9readT0TOFct7SHbKcxKzvGcaZjDBXtoyhvIxlBWSvJMErFUV5TXUU72TyOappDms/eaaG31phbmtOz5Ifyi47to0Iq20ZQ2UbnY8LPc12TqOmeQq3wkWLNjuYRD9on/OiaCaPPFsWgM4ERzyLGfMuYCFzAZOgipsP0Ib6M2ciXmIuSfAVbzJDoV5iLfg1b7GvMkUSlzEa/AslMRMp05CuQTJHMJ2Vy/itsloixI19jiuWGw0CPMTP+jJicEXH6pYhXimt77Es4Yl/CFf8Snvhl+BKXEVy4hNDCRYQXLiCysILowjLiiyuILy4jbpDWwuKSIKwkaSUJa8sSVyS+hGAkAU8wAqdvHnPuEKacAYzPeTE85cbApAt9E070jDnQNWpH54gNHSNzaB+eRdvQLFoHZ9AyMI3mfiktAzOirFUcqc0c2oXY0DFMfQ0dw3Noo779U2juk9LUN4mm3kmc751AY/c4GrrGUK9JQ9co6jtHRXljz7hoR31ofLKjfWgWHSM2YWf3uBO9k270TXnQP+3D4FwAw/YwxpzzGHfTT57QH1OLC5n2JaBElU26o5hwRTDmCGPEFsTQTACDM34MzPjRP+VF36QHPeMudI060TnqRMeoA+0jdrQO29AyOIfmgVk09c+gsW8KDT2TqO+ZQJ0h9b2TaCDpmxL11EYKlU+gvmdcSF33GNJJfTfVT6CxbxLn+6bQRNgT3oTziB0do050jTnRPe5C97gbvZNe9E370G/YP0DnU16BT/eYE50jdrQP29A2PCdwbOqfwvm+STQattR1j6O2eww1XSSjONc5grMdUqo7hlHdPoyqdnmkc6o71zmK2q4x4XMD2Uk6Tb3jaOgZQ333KOq6RlHbOZKUjmHUtA+jpoPKRlHfRW0n0Ng7KfxsGZhF27AdneTXtB+DtjBGxJ9pSGDKv4jZ0DJs4QtwRC7BGb0sPsRu+iAnvoJn4St4F75OK56Fr6HEvfA13AkprsTX0MWZ+BpXLPGv4bTKGvpcib8gRRb+AhfLDYOBijU9Bt0LfwGJR4iMZ9/i1/AtfgX/4lcILn6F0NKXCC9dRkTIRcSWLiK2eEGQVmJpBYnFZbHSItJaXFrCIh2Nc0VW+nHLrbhiiSWEIgn4ghG4/fNweEOYc/kxZfNibMaFkSknhiYdGBi3oW9sDr2js+gZmUX38Ay6hqfROTiF9oFJUzoGp6Ckc4jazKB7mNrPomeU+tvQOzondQxNo3PA6N8/ifb+CbSR9I2jpWcUzd2jaOoeMaWZzrtGRHlL7xhae8fR1jchxiY7yJ7ukVn0jtnQP2HHwKQTQ9NuDM94MWrzY8IRwpR7HjNe+ls0Mdj8cSH2QBz2QMIQWUb1s94IZlzzmHKEMGELYNwWwJjNj9FZH0ZmvBgiYp9won/Cib5xB3rH7egZtaFrZA6dw7PoGJpB++AUWvsn0dI/geY+KS39k2gdUDKFtkElVDaBlv5xtPSNo7lvzJSm3uR5M+HTPyF0UN92wpFwJnzHHcIeuuEYnHJjcMqD4RkfRuf8GBP2J30YnvFgcNKJ/nE7esfI9jkxXx1D02gfNGzpG0cTSe8YzveMobFnFI3dI2joGka9ks4h1HXS9ZAoa+gaEW3OC5uVnZNoG5xE28AEWsmv3lE09ci5Pd89jPNdSobQ2DGExs5hnKf57hlDS++4wLB9kPycRfeoHf2TbgzP+THuCGPKE8WsPwF7aAkusZ9/Ed74JfgTlxFY+FJ8kINL9GH+GqFlXf6C8LKU0PJfoEtw+WsEl1IlsPQ10stfEFiySqa22cqTOoJLf0FwWclfEVz+K0IkK2vJ/yC0wnK9YEDzrkTMvxED4ZW/QspfML8iJbLyNUiiK18jtvIV4itfIrFyGYnlS0gsX8TC8gUsLK1gcXkFi0vLWFhaFsclOmYhLSKwLUdc8cQS5qMJBEIReAPzcPtCsLv9mLV7MDnrwviME6NTdgxP2DA4PouBsRn0j86gb2QavSNT6BmaRPfgBLpIBibQPTQpynqGptA7PI2+Edm+f5T6zmFw3IahcdI1hwHSMzyF3iGpx9Q1MI7OvlG095KMoM2Q9p4RtPUMi/KOvjF09o+hq38c3YNyTBqPbBsYn8PQpB0j006MzbgxPufBpN2PGVcQc5552I2f83cFYnAF43ArCSXMc6pz+iOwe+dhc4cw6wxixhnEtCOAKbsfkzYvxmfdGJ12YYRkyonhSQcGJ2xi/P6xWfSNzqBnZEpg0jU0gc5BQ4Ym0UUyPInu4Skp1G6YyqnNuJCOgXFIGUP7wBg6hMgy0qX69xKOY7MYmLBhaMqBkRkXxmbdGJ/1YHzWK3yfcgQwbfgw49R8EDcnDgxP2qXtY7PoHZlGD9k1NGnaQeO39Utp7RtBS6+U5t5hNPcMoamHjlKojtpQ+3byZUjZSv6No3NgDO39o2ijNr3DaO0hGZLSPYSWriG0dg+jrWcE7X1j6OgfRxfNMcUTxdG4HSMzHkzYA5hxh2HzxcQLRp75JfhjKwgmLiK0cAnhxcuYX/oSkeWvEF35CjH6QF9IJ39B7IJVvkb0gkwClAgyyoW/IJpOjD4qmWQ6pui16Ild+CtiF6XEL/4V8Uv/s0oSl/4Hplz+HyQu/38s1xEG6eacysw5v/RXJC79FQtC/oKFi19j8dLXWKTjxa+wdPFLLF64hMWVi1KWL2BJiCQvIq2lZSKw1duDW3rFlVhYQiSWQCgcgT84D68/BJfHD7vTg5k5F6ZmnZicsWNsyobRiVkMT8xgaHwag2PTGBydQv/IJPqGJ9A3JKV/eBL9I1MYGJnC4Og0hsZmMDw+i+HxOYxM2jA2KXWNTdowQvrGpjE0SrqkPuo3QPoGx9E7MIYeIaPoHhhFT/8ouvtG0N0/Jup6B8dFOxpTjjclxhuZmBNkS6Q7OefGtM2DWacfdk9IbIe6A1F4jJ87oZ888YcT4jkfPesT5+E4fKEYvMGoWIW6vGE43EToQSE2lx9zDh9mbB5MzboFwRPJT8w4MPb/t3dm2W3syNb2mDwcj+R/8sN9ua93CJ5AjaHWuVW3Tp1jqyclUQ0lqpdb9ZK7E//a0SCRFGErZauBa2stLFLJJIncAPEhAoHI/orM9AYyvbAsU/NLqtMfoRO08qLHcHymJ3/O9uXPWTz316fm5Xctc/L71Jz861VT8L++Nr2Q3vtyblGmFvyal9ZlYXlD+iubsqhlJMvr21b3jV1ZRRnuyGB9269hKAuLazKHuvdWtN6v5ha93gv6Xf+amtc6/N8rTBJm5Z9/zsg//piW/43y7yn57d9T8r9R/piWf/w5I/98OSt47+/puufl33o9s9qe/8R5f0zJP/C+319p+Qce//VK/vH7lPwT7f3nrGg7o41n0Pdwnasyv7whADAmFsNtpK55J9uHiJg6lv13p3L44UxeH537rPNC3p5cyrtTlCt/jOf4/+7K29MraZWTS60L6vP2xF67/v0f5f0Zyif5cO7l4rMcpfJFji6/yDHLL69B0+af5ejSSt7ueP0Y5RKPn+T4/KMcX3yU4/MrOT6/lOOzCzk6PZejkzM5OjmVo+MTK0fHCixAC9ZUDqlJzx+dxQUfJ9J87O0fys7uvmxt78rGaFvW1zdlsDKUpcGaLC6vSm9xIPO9ZZldWJLZ+UWZmevL9FxPpmYW5NXMvLyctvJqpidTsz2Znu3LzNyizM4vydzCsswtDGS+vyK9RXwWyoos9JZlbh6fF5/pnzvbk1f4vCmUOfnzVZRZ+ePlrP6P4/r69Lyk75zry8z8osz1lhW2/eU1WVoZyvLqpqwMt2V9tCsb2/sy8jt+7uy/UTcpXKUoe/64u/9GdpAOZfdQtnYOZHNrTzY2d2WoZUfWN7ZlbQi4b8ryyoZ+x9JgKIvLa9JbWtXvnu8PtB6zC4syPdeXqTlA1Qt004LjfZmet2LnQM8FeQlNvfw5PSdW4tiCvJzFZ+B9izIDffsDWVhalf7ArnewNpKV9S1ZXd+WtY1dGY72ZAPXgTLCteyka7C6Y5KyKgt9TC6WVEd8vtUF0JiXP6ZR5uTfU7Py+6sZLf96OSP/ejkt//dyWh/xP17DOTj3T/QPXLdf86tZ9JM5+ROv4zx8zstp+f3PrPyB5zPyx6tZ+RPtPL2gExxMnOZ6AwXt0gradEcnFphk7By80xDfw3fH8ubDqbpH3h2fy3uUkwv5gKIzUMxCbSaqj2eXclQoH87i3EtpPcf78ZqXo7MraYp9Xvu74vtQhwt57wXPW+dpPfyzfAA6ufgkJ5ef5PTys5xefZazqy9WPn6Rcy1f5fxjVj59lXOWX0aDs49fJC/W5tH26Auf5dzL2dUnObv8aOXio5xeXMnp+aWcnJ3LyemZHDu4jk8ALwMXgFQluODbfPPmrRwcHMre/oHs7OzJ1taObGyMZG1tQ1ZW12WwsiZLyyvSXxxIb3FZFvpLstBblPmFRZmb78nsXE9mvMzO92UO8JhfVND1+njPQPqLK7K4tCpLy2uyPMDnrcrS0or08bqWZVno4XOX7HPxebMLWqZnFmR6Zl7L1DQe7bi9ju/Hd/b1ffO9Jf0+wHZ5ZV0tx9X1kQw3txVAANHOHu49g8SSb9VNenD4Vq1OPMJtuo/XUPZfy87ugWzv7MvW1p6MtOzK5mhHNja3ZTiERpuyqmVDBqtD/c6AfX8J17Yk871FmVtYlNmFvkAfPOJ/LXgtir4OLRdkOi+z8zI1Oy/Ts3ZctYbO+AxoBn2h7WBdBmsbsjocKVwBp43NHb/ufdnewbX49Wzv6XUMN0ayqu08lMHKurYL2nmhv6z1Rn1ntPRsojIHiGCyAKCgzMqfY+XlzJwAUFOoL/oHrquH+uL6/frw+sycllfTs/JyysqreJzGa3bNmCThWgHVuM4VbdNdGW0fCCYg+4fv5PDtB118fvfhRN4fncqH4zP5oDNNzDjPdeZ5jNlnKpiNXshxlLMLnaFilhrHWq+f2vmtY/l78ufpO7LvQx1OzrVOH/y51aX5Pv3us0s5Ob+S0wsbhM6vPungdPHxs1x8/CKXn6J8lavP3yp/ycfPLDVrcPXpq0ws3u7RF67QJ9A/rj55+Sjnl1dyfnEpp2fncnp6JienpwJoaTk+VmBVCy74ON++fSeHh6/l4OBA9vb2ZWdnV7ZGW7Ix3JT19Q1ZW1uXlZU1GQxWZXmwIkvLA1lcGsji4rL0+0vS6y8qyHq9Ren1cWxZ+ovLsri0IssAyGBVBoM1WVlZl9XVoRf/TLyuZUVBtpR/bs8+dwGD1kJfy7wCCs9xzEqvt6T1sO8c6OCLQRgD8vpwU4YbW7K5tSNbO3uys3egQNo/fCMA1eHrprzG88M3Wg4O3sj+wWvZA+R2AXTosic723uyvb2rcB9tbsvGxpZCfpi0wvWty8rqmgxWcG0ANsBtmvQWl9JzPYbXtPjrmZ6YHOgEodeXeS0YvKE34Lys71tcXpFltA10Xd+U4eaWAgmW8/bOnkJ3dw+TkkPZ33/t5VBdwzFJ2dzYUgijrVfXADBMLlZTvfFd+E58NyCMuswt9BRCs/MLClrANgrgBEjhPK3votcXj9pXMMno6aRnbn5BZudQ5lOZmcVzvG6TEUxmAFNMdqJdhxvbMtra1YkFJhmHSFnzDmG9WHyGHx9ukaycYMZpRV0mmH0q1OBCOZNjzEjHS/aeeG/rMZ2PGa2V9Bn6+fiOrA5anxP5cGxF6+f10M/Vz7PPwUz57OJKzi8/6kB0+fGTXH38LBigPqJ8/iKfPn+VT1+a8vnLX3KtfP1LPrNUq0HevpOeox+k8umzXGk/+SSXVx/l8vJKLi4v5ez8XE7PzuT09FROTk60HP8K4EIW4NevX8vhIQa3fdnd3ZXtrW0ZbY5kY2NThsMNWV8DdNZ0QF5ZAYhWtCwvD2RpadnK4rIsLw2sLOP1VQUeBvI1lLWhgnC4viHD9aF+5trqmqyuWFnB+Qq5Ff0M/dzFZVkCBLUsyWLfS/yP15dQh4GgLgAFIIsBGNCC5bg52lYXKFyhsCoBpAMA6vUbAazgKtVH/O/gOsQ5B9BEiPAkAAAgAElEQVTjUPYBu13o4kUBBo12ZGsEnbZUq82NTYW96rU+VOCvjmkVdcQEIErScoDB2fRcXAL4vSwu2fVDZ7wOWEGnFbTHuqxCS1wr6rG9o8DCmuXe3oHW/+AAbevX6teo17Z3ILs7dh2A8CbaWwHs8AV4vZ74zpiw9BVADqEAESAVpb8ovcVFwXm4Bq1zdm19vIZz+n3p6Xt6srDQU5jp4zz+7yvkMDHCZ6Bdcb3Rrpub27K9vacARlu+foN0NQjphb8es0mUk6aEbx+P6t+Hq8Rfz18bf45zxo+N/Q8XTFPyNYRmHUEXwT2KC3VEVBfKB69LfMfxMT7rTGfJZ+cXcn6BweejXF4BXJ/k46fP8kmh9UU+f/mq5cvXr/Ll618Ty9evfwlLvRp8+fJVJhZtc7Q/+oGVT58/y8dP6CPoK+gzV3J5eSnn5+dy9quBC6ZiDi6zumBZYFDGgLwpmxsZaNYAIYBmVcuKAmwgg2Ur+N8KXl9TYAF662tDAbA2hk0JeK0r2NZkDQOTf3Z8zgADln82HpcxiC013wcQ6DkOUkB1Fd+H79rYlM3NLYULrCSAZ3//QIEECxN3+tS7ffrja9y2GoP8waGecwDIYfDf21dwAV5W9nTAh0YAPOBlWo0E8DKAmWYNmAHxyWV11bXE634deq0K4gDyQCECK06vUScCdp3DuM6tHdnZ3VNgAUy4xgDWGwzsqbyVN7iNAcC8ty+7sM4ShH2y4hOL1mTFIRyTFQMrrCFAKitLAaxlWR5EvTGRwbVgogEQoxjA+g4wQCwKwIZzMHnRNh6sqiVr7TqS0WhbLWDAGdaxgustdv0jOgrwyorCLP7P9qzE3hUNBW5Cg+O9aX+LQibb74J9L1oCPhaZhYVuey++w7IQNLeHsOSl8G7gthH2iGNW57zeACtACBfP+fmFXFxe6Qz6YwYuDFY6oPkApnD66y/5Olb++usvYalXg69fv8q3yhftB+gLX+Tz58/y6dMnLR8/fpSr/wRwvXn9Wl4fYsDGQL0nu2Pg2hgCPAAQCoC0qmV1JUBlj6sYYFBW8PqaAEp4z3ACuDbWhzLUz1uX9VV8ZlMCjHhcyb8DFlWCoz93iOp78J343OGGWhCj0ZZsbWGQA7j2dKAGkGJgB6yiKLDwmgJrX8/dV1jtyd5OXnZb4DJ4bcnW5ihZXpsAtA7+E64JoHJYAQwKt/jf4ZVfo4Ib14zrBNihv1+jQWsko61t2d7ZVVevXVtA2QbJd2/f6yCpAykGT1iZANs+rEm0965OVrZ1sgIAj01W1mxSYfCFxWdAXVqGVRgg8ke1sgxagNVgBdYSykAGA0w8ACQDl8GrL4BXKj08X5SlxSWbqCwP1BKH5d4C1/auTiRgUcJiBpgVBICBF/z/7u27VAIcWNdNRWECoHiS0Xf+3HUKyAA4b/wmewk+eguITFt9Lz7bbn8OT0YqOpE41AkDvBva7/Q26ai7t5ODDPA6OTmVM8Dr4lLdPldXH3U2jZn15882WMHasoGt3sGZYC233beghdfuFlw2EYt1MBGR//rv/8HDd//wu4/3TXp8MukgjuGNN/nDuWFxtcEFKwIDsVlcNwfXiqwOUFbVglJ4OZxgYWEw34A1NAlaDjtAMQdX6zk+OweVPzeQrql7DuCCZQfXVwLX9o7CBoM0rAy1vPYPbBA5MFgdqGW1ZwM5QJcXvF/Lrj7C2toBLEZbWkyrkYzU4jKrUkEfMJ5QZ7sOB1d6/TqYx8GFNceAs1qVCmeztnBdYU1iYMagOz6Yv8cxDNxwDwPSObhgQW6a5Yg2t4kK3Lxuaa/aRMKsJ7eg1HoKEMHaWhIADdYVAKfw8sfl5QxaGax6vZ5aW323uq5bXCsKbWvbTXXPwkrc3UF7oh3NgtZrxnV7gWUJ969Z1zY5SxZ1WNbJOoWFaqAxazUgY250wAaTgoNDWLNeFEzZ57vLXSeA+5j8wALOyq73K7WMJ0ykHGTv3mHTZwOvC4cXZtKYVWN2bYMWwfUrg4/gKlAsB5f+MPf3ZW8Ps+8YwDAIh7UFMGCgBVgAEAyymA03rrsVzI61GLwwOMMFaNbXmltfsMDcytLXYaU1A7Z+dvzv39N8Xw6u/LlZePo9bo2Yq9DgBasIsAkYAWAIRFGIYWDB4L3jMAKQxssIkMqOAxabo2RlBbDU0nK9htAqgKSWqF2jgT2u1y3UuF48Zq5RhdbSsrpLYYWpnplVWQJXglYOLrjE1BK5IbjcXQh4JXCFO1PdmOH2a1x+sJpgRcGi0hIA00ccW5RFBRZA5WVhQRbGClyGBi9YXuYuxPon6gGX8+ZGtOtOcgErvDIL+jWABAta3b3u8oU3AW29u6tWOCxxuFf1GCYuqUSfsNe0fwA6WuIzsMaGdVNMhKwAUvbZO7K9jf4Ci98L+oxOBs0yh3s575cxqQIcse7awOtMzs4uBPBSq+sj3EGN1RWD2/UBvPCj5+FqFLjepm3rLNo+rC9MaMJlGO7Ci4uL1jpXBGkgQCNKyQDKj0O0R2NxYbPZu3cITsDsEov5+OFh7WZLRhsNtNSdFRBpDa7m+oH7ZzlcO/44WGogpoNuDLw5rBx0A6xlaHCHDdI6YKd1M4NjADJ3o8VzA5u7KFsWCQY5zNBHug4VQFKLSUG2o0ADqNVN5mtUsVY1/jjCgAlLDufBqvOiFuS4FYlBPoHc4R7rc3iMgusEnHT9znWAhhqYsiRL/aU0eCOQQ+GVXSMsS3WHwpp0i8vAVba4YJG8cVfhPgbvLVuvS67C4YZOLtDuUfC90Btto+4+WFq6PtWThR4CKgAgt5zCmlrEWlWUvvTjvPl5mfcyNzcn18p8fFZP+j1b78LaJlyVCPTR9VJtVwz+ZnnpRCR39epkxFyguh7pIIEVPhqN1CKHdpv6/5a6W6FjKuo2xbkAjj3iffZ+/x8THHwu1jvT5+OzscYKlzUmfT7xc1e76untp56BVv90K/LgULAuibUvBG4gnBnrXYgUA7wmWl3X1rOqGZ9Z0YICBFdBGIAL/npzg5hrY3fH3ISbmaUV1pW6fTB7Bqgwq8bsGusRWVns9WVR/3eYBZB8cDYoYaC21+Mz0vuwKB9Fvwff52Xss3A8h1wa2DHgpsHdXYc+QCh4fDDCgNQEVthgndbddHYfA0/zaO5OW5/DuWE96jrdGJQHDiCFOq6pH5oEkFwDwEkLLJJFWcRgrQWDveupEwK43sLyMpdhWF3NGlfmNlOLK3cX2nrP2zdwoR2KukcVXGZRbiEyEdGRbm0li7EFLUR6AlqLCqKeW0sGogY4sKjSulVYWTgXwMphNTsrs60CkAFs8Vmx5rXs1w7LHe2BiRVAAnDABWdWklnP5tLFREWvKa0/buj6pwYG4Rq1+DFcd14Ab0TAekBRghCOR8H5cKd72dC1QVioWBNs1meTu1R/OxFw0m5HXZfdwARrW61IREu+ffteoyQRrIH1rmtWlwdp2My7PRv/66/Cj56Hq1GA4Co0VQtcLTchQrsjEMNcgoMAlg7A5vIBbDCL7i80pTe/IL15/N/XokDC4KvFBuYluJTwXszQUTBIzWFQ8//xefrZNmjrYK4D+tj/OKYWScCuGRTUytMZurkodV1IZ78NyMyicssSLrHctefP1dUJd6e7PHXGHIDCOQCJW6Hm5nPrCTrFNfv1Q5PQI/Sxx1w/0wMahi6qJz4D1wpY4/vw3e42RNg/No5rAMq+RRRifadZ9H/XuAk16OCNW1z7shcWV0RHujUJIGukp25XyK0tgMvaUS2o+YVkPSm8kuWVuQPVLQgQmaWlFlYGq5mZWZnJ/se+rpuBq1nv2lF4tQNndL0OWwW0AESZ2xOBLlr8mG7XCJjFdo14LWDkwTFwA0MfWFGAH9YD9bPxme0IStXK9VI3qfbrxopEVKy5gC34BG5QgBhbMRAtifD5xuqyQA1EGH7fXVj40fNwNQoQXIWmasCFAAWEe8O1gjB4/5Hrepa5spZhXekPMIADQAE4802ZnZP5mTmZn52XhSj563iO98zjPThvTuZmZ2VuZlZmp2dldgb/W5nH4JXOx3sCbv69+jlt2PUAywilDpcl3HVupegAEWtubi2FxbSGNbtw38VjuCuzdae0BpVbgW5NheWpcAKQAeO5hfRoWrlmqs+C6gQdoJk+QoNWmZU5vIbPAtBTxJ1bXwqvDXV5NVaXRa214AXrywMz3iIIoOAq3MLet3AVKrRs+0PbTWgTFwOXwSisKMCrWbMyN6KtZ1m7z8+bazC3sm4ELgc2tlkki2u92fIAd2e4gCNwxqzHiJAcqtvTIiNtWwEmALbfcFX3KOqeQ9+zCKjZuWE92f7F/P0r+H14pGdYWJjgpd8JgB2TszRBw28Ax30isuhrmOEGHW7qJASh/oiWtLWuMXehBml8b52r8KPn4WoUILgKTXUdXPjxO7g0uADWlrkG48e4iB+jWlUGLAxYNvACWrMyN20gAoys2EAcg7KdG7CakdnpGZmZmpbpV9MyM23/zwJkeP8YxPS9DjQFmw7oAUODGwYKtdbUGmvCquFSxOAbEBu3oAAkuPSSm1Kf52tOmZtPQdW4SMOKike1QAHWgLdCaT5BPbQAoAB61Qy6Ad5aoIM/n5pxoJsVgsAFdcVG0AIGvLWhbGCtC+t22VpX7FNLlhfCuTWiEK5CjyrEhupsjcusFF/jckuzvb7VHpjN9TffrFP52lUDrwVZ6AG6ZpnZelbbPfh9cIWl6VamugoRoYqoV9+rF+Dya2muA9aTWVC4DoMVgIXMLoiMtOfNhnnfEO/n6sZ4hPPH+Qo7i5bEBm2E+mPLhkVamjZwkbZcqKnP+m9FJ2TWT2FF695E36sG9+Roa0f34yGzC8FVGLz+Aw4TXIVGvg6uzOL6JrgACweXWguzBi0Flw26Cq1rEAuYNcAyaE3J9KspmZ4yeBnAxuCl3+OWCQaC+L9l0S2kGa65Gt01GWtjYUHFOpEOzB7VCFeor9WFa9LWnbD+5GtODkOzqHz9SV2ijWs03KZqjWbgAsTCGjVYZZaVQyuBC7BygM34c0AcVpeCOazKsEIQsIA1PN2zZhGTaa8arKtwGyJM/LVtQI6ou/2dPdnFoI8BH+5CrAdhXQdrhA4udaG6OxTrivkal4Jr/jq45n3tqwEYwBuBGGPgSm7COZnFZAXtm1yOiFQEuDDxsOCMlsWVg2sigMPtZ5ZjgMugZeBSAHmmF2Re0YLsJAlqHpSioLNtALqZGv+nUH9EWZolqtCKtTyffMUkTCcrDq6wuqBpXNtw/fsWF12FhQHtFztMcBUa9JvgWse6zg0srgDIjMNreqZlQTSWl8FKrSm3shRaam1NydRLB1cOL7e6kqWlg3dYeoCXuxN1fQzHG3CF5WXWiW1mjUCOxupCuL6DC66/MXAFwPTR16kArWZdytymAavWo7o2rU66fjcJYi2Lq7G8wtoKkOlgh/fDxZQsriW1GOC6UovL17nGs2eY1dXsbbpmcSH6bhxcEaARUYXqMmyvdcIC7/fh8mrWuGBNRbTgZHA1gJudmxMrgJg9T9GF0A6uNWitkPaQeHenTQYXws+b6Mi2xdVkfAlwoS/cxOJqne+bq7FPLVKd6X61lBGkiZyEDvlaXgJXPgHpWbg/6hIuUAScxBoXokOxxnUckYVpP1e+xlXay1X40fNwNQoQXIWmasB1mK1xYda9KRtYbF71wUrXcyyK0AZuW2fqtawuc4M0oArrKnuEK1DdgDMyC0ABWg6ucYtLra4A15hVZetdBjCFlbouM1dhuAvzQT6LQGzAFXutsH8KbsGI7nMrKweZB4uoJYfPL5YGbFjj6s3BtWrrXfa/r3kpyGKNyyEcVpmvE9q6l69vJWiZ28zcS83GXKS3Qlh2uApbFle2KTfAlda4AC7PnNFeGxpa5hNPydVyF8ZAHeHwGbzaa1zmIrzuKgzLa/xxXuZgqbSgFW5Cu1ZA2jazI6imWeOyrQ5j4HIAI3OL7keL6Eh198GKspyRBqdY5/KgDT3X1sJyV2ADKsvDaPBr3OnqJszD/sNNmNZkMblq3L0WnGHrdrge5I1EUmdkBPlmVCH27DCqsDCy/RqHCa5COwJc71rh8IjKQjj8pm48Xl+zzcYRLach8Oo2i4G7DTANPlALLAbibP1LXSaxboX1G3cXZtZXwMrghiANW9cBqGBBKQAcGOP/p+jGsIzcrQe3VoTNt9a4ENTgxawuD0IBpOFa1DWubM3LPw+RYcnq8u9SCyy+Vx/hWgxrrC+LGKjgUpxvoNZH5KUXiyD06wOgUmSmHQMszXLEAGlBGbC0UlQhBjzN32dpn3Q/F7JJHJqbsJVRwl2FAS4NiUdEnmYDgbtwS/IAjZQ9A0EIaeA3d5lZXcgxaPu4rllZvsk49nnNR1ShWiMOKV8TM0stQBeWlkNa1ydxvYh0jVB49FGLKkQIeQtcmkMyQvs9rB3Rf34Neh24Fi3uGvQtFJoMes2TJGvUYQRn2DpWY6mZxWZbRNx96FtEbJO1WV/aT30iFRY8NlUDWGot+740RBPiOhAdqRGFr2FtTdjHdaPADITGF370PFyNAgRXoamOxjcgY+f/DgavyFeHDBeeKQNZMnSzLIIUvhOYkFkjCTBuFenaT2apmQvFrTJ3BeYRhRop6AN3+uErRDy0PAAVj2PAMWjlQRmxToKNrJEv0S0vDCapxAbq2Dzse8kUbE2gRuzRskc7RzcUA366b6sBof6PY2nfllt4cBmNHTN42nsxWCYrEbD1PWZNaivLxxibcJHWqJX6KbO4sN6lBcEZSGGE7A+e3ko36qa0T56aKzbQIvxbXYc+mdGMKb6uswjQGMDae7f60sdr8Tpciw4ze7T3Ne/xzcrQGH0tC/uPrBlqZSFkH5vB0/qWuQkjqjA2mtu+tEhhFdGFlj8zZQTJwuBtz5YBEdo2+70aV6PBzgIyWs89aEMtssgckvXFmDzhmswtGFlAMOloW8tNNCHSPk3InPFda4vgKgx5VR0muArNdXSEzBl+WxPPnLGXZ87Q3f6NO832K+VZHtwicZeahoOnzbPNJlpYH2qBYM+XWyIGMHPvwVIbD30H8BpLIwOFuy1zi0ihkWfv0HMcImODPgbfNPB7/sSUVxBWzKTi0YhqseHzsvD4PAMGjrfAl7KHDFKoPULuLeweOkYGjfy5A1P3h1l9kC3C6uzuMQRiZNlAkLoImes1B2NAyzPgw9oKiyuglRILa0qkErjgLm42XkeS5TztF7KZaJBCljS3yZQREEL+Qn/uWTSQTd7Og0VlVpVlgp8MLN2Dh4CRAJZuKEb0axNRCDdpAlfK3G/nQCuATpMHx+bha4+bdhscnJvyNQJi2HDs+7QyC0wTJWs4vLVRJINuNhs3qdB04uEWcgBYwatpn5rMH5ru6fUbzS+J27NEot0mV2G+tvVFvp1kt/Cj5+FqFCC4Ck1lFhfA1aR8GgeX5tzDTBs/PI8sixRFmqZIs0M0YLG9TO21otb+poBY5voz15hHzOH4OLRifQoDvUIDUMJ3ZlaQwwr7aJoyZqlk0NJ1Es/ibpaXXWMrTF6vO8DdbDZWHQJmYaEpaDxHo+cmxHmWMT82KdvjarxnwmOTXd9hhVD34YTUVRiod7CmVYBWgCssLN+7pWHwcfuWsSS7aY0LmSBybTKry+4OkLvPABsDkMJIQQQwBZSaR80k79nkA1gR3afW1ZiFlYCFtSxAyzNg6D3QUvYTS9M07irE/3rLGWQD0fRNYXkBUP55DkKDGtJ55SmeLL0XvjcyYpiV5mtgAS31SHiWDA1mMus+3NL6GHu0NAF0tmnaJxy4IwEsZEwwkMkft0fBvbksO3yT6gn3Wrp5gt3Cj56Hq1GA4Co0la5xIVchsl3HLU3CVaiuEgyeMXBboAaCGAJccH+0XWWZGyxzk+jeqDzQAW69tAYU62VuYSnYIox9bH3KrSdzWWZuudwCyp5bEuDITGCWVlhbCq5kccFlWACXu8cU3GGNJUi5azH97xYSBioFPWC3KmsJZPa/Ag0ZE9L7AnCRlNhuBTMJWLAqNFlwlmH8mqUFaOkaV3PbFgOWJ55NOf1wuxbL52cDvSUPhmWi1hZC4lslS7SsKY0wkbBJBEBk4ApratFueYLjWTFgmZVl7sDMJdiySuz2NAqZBCzPFdmyuCxtl0IqYKVZQAAut7gcXGZ5mZtRrSq3rvS4Qms8VyG+D+fDbei/BbW62pZ5C1IxodH9XX4eJkzoa2ope35FvVOB3WIHkZ+Ryd+gNbbhGLc0+di2tpoEq+OpnuL/wo+eh6tRgOAqNNV4VOH+HhbpLapwU9d/PBu8DrCx1tNYV8ldF65CwCqex5pNdszCyg1aDbiaIAZNqOprVZHKKV+jSgME4DTmDjRLLCwye7wGLgwgY1ZXnm9QAeNwAnjyoi7EDDRaF7WY3D2YXgs4jT8GqHA8W0sbe1/jygwry+8p5sBCLr7IbG/3FvPbs2SZ0XWNCy7DvLhbMN1jLCWhtQTDun8rDdKIwrMEu3CJpbWtsDJam24BIYOVrlWpG9DXrvwGk9fch26NtdaxAlo+yOt6U8vKyqCVkh27VTQGNkRY2p2p80e3uMLKSu/BOfgcWFvXwYU8hLbe5etckYMwWVftPmeuQre6oi8hAANWsydETrdjgZWFe4m99YS6uIlkhL5rUt3JGeG/7SIkuArDXXWHCa5Ck3348F7evsXdcJHyCUlKsRHVMsNbrroYZCPt0+Qw8VjDiscmys4sp3Rcrawmsm48SlDXtLBGlgVaxKJ2C1oeum5rW213YbgSA2TxPoBH79ulj01EoSbHxeCMgSjWqBJMAjY+ECVQ+TqXrlHZ+pS9t1njuu4ObF4zi9Hh2vpOs7gQOafWlq5jWfZxWFltYDmY9N5QjWVlsLLbeSjYErDMutLoQV8PUisLgzbcYeEa1CAMWApmYWMgDg01Q3+24VZdhLqfC6BqB14gknA8EKMXWePRvgov35+Vuwj1hpG4/nH3oEMK4En5B2MNCmt/eTF3YKyJmSvQj+G9ut6VgdDXwCwTvMMruRfxuQbyXBO1NNXatA3Z6lWIpNBu9atu3t+GGvmJIIy44aclQ86hdXLSWFrXEupeC8j4+p27Gxd+9DxcjQIEV6GpcItx3K0VeQrV2trB7Bu56oayjlDhsGzcagorSdegYo0q30MVz7F/CWHdvl5l4d7tHIM97M3CXibP5xebhwN6rcCMWOOK+mAdJVlmltZJBw4NfYd7MYq7E8PF6G4cddFhNuyAUstMYdhAUAMnfAAK12g8mnvUQ+ZTxnePAGwFXETQxbIMNMTe3KwRbh+Rg813mctQb92RzdAt+KK58WBYUhFk0TyayxeRgmZZIf9kBiyNGIQ70K0MB5bma1QLy4CV3H9+k8jGvefrVXoc8GlC4SODhoW1+/4shL2ncPeFLBuGu4UdXhoajrZQC8X2NCWLyyETt5hR68f3cgHwtu6UJ8PF80iW66HwEYiBbO+a8d0gFmtbuo4FUIallqAFMDbQwmTI7orgexq1D7rHAJMyj341iHmgiSbRhatwI21Z0Jtfavb33NI69duXRBb4q8w9OL5n63vQYlRhYcir6jDBVWguBdfr1wquSLCrm49xWwaFBNyCzXqURgJib5VnrIi0SxrSrptmPUmuJ8ttzsN72nu68L8mk43Pi8wQCXj5QNAAxdbVvE4+WMSAAUsNe4uSu1ITA9s6mVpuAKCWPJoPn91cp95ORN2dFjF5zR2aXKHu8tSM7/6dWVh7HvJuz/OQd7zXitZVA1zsGjFLx/4sDLDmWkIQRr4/y0PdNfgCriYLb1d4wTXoARcR4h6biyOdE6wVs1hsHUsHfgWGW1itJLHWBnABhhWMxyZ83TJnBLRS5gtkxbiWDcP35GWpnPqR7R6WLNYBM3Ali0vD3s3Np8l/dT+Wrb0B8HBj2vvs/QhR18S3eE3X5wxiGtquoGvvA8utN430CxdiQF034iM7vkErXT8sSp2YedJk32Bs2zfgNUD/CYtyNQMX7pt26Al0IxDDLK2zc4MW7rt1/W7HX+TLF8uS8b0BzV4v/Oh5uBoFvtfOzTrnV70j9n/MjSTfv3unt3DXW4zrHYDdTQg/vgZeLOqtOZAlAlkyFDaR/FUzuiNBriXJRRaMeK45B1O+vbHNxrrx2I9FHj7Phg7QJQsM1luKLhyHiM1yk0WHzb0x481gpkDzWbBCDTNkd0UG3JIbU6+xsRTD8gsrc2KmDNTRrUt93W/nkjYcax5D33yse9smuUlRdw9G8YSryJUHawIDqd6uBPea2kM2hQZaCqw3dusSWM34XwMwIsQ9bvOBrBi44SGsCAzGuI+VWh5urWDdStfc4Lo0K9Juv2EDM3INhstPNU7uPtTbbyCpVlU7C0YZXHkqJ09bpdCKm1bG/qZw5cUalK9RBbgyaNl+Kt9Q7DkHG3g14Ap4IR8gUitds7hi7Sxzn5rLHFk2PIFuDwl08XvItnJ4PkLb0gHd4DqNBM+WY3F93TaJ7+5aVox0o8ijSWHv4zeL/CKT77kV61mTHqsZn1nRggIEV0GYcXDFnY+HAS4d6P1HqhbSbErVFMlxp16+klcof76S/Pmrl1MyhcS5r+wRuQijIBO8lpdI+RTw8yzoLWsNg4O7ldzS0Zk/ZrsxcOhjzH4tQjGF17vrMgBnAHY4eYYKA6Wlj7IkuE0i39YtW7K0UwZYuDon3cbFb7+SuUD1OzTFk3+PWpnZ97iVCTBoVoXBSpZ/EJuL4Sb0CLQIc882FWv2d7W8EE0Ym4qxmRzBNmPggptNS2OtqEtY12vMBQYgWaJYH5wBLwzWad0KA/N1N2HL4ko3i0TOPrgM3VWon+EDO6xfdRECWhHBaOtbCJawG3168EiAF26/cBGurqu1pRnc1Q3s2d89I4bdpgTgchchHtdiLxzW9navoRkAACAASURBVJqyiZtShqtQrS5YphZtirUt3PgUk51Gm3nde6i3c4nUZOo1iAlXDq41wRoXJiG4Xclhukmkhb2fnp637nCMsPdPE9a0vn6dBKjSscKPnoerUYDgKjTVOLhSYEYLXH2DhIOryS847SACtF56MYDp/y8BshxaBrY4prkJkVgXtzNxeM1Oh/vQ0z1p8twcXL62hVlvQMkts3E42X2/bF0tP1ch4u+1FFU+AOH6Ujb7cGvaOtwkN6e6QQNcM+4+9ce4nYmdE685qFTHLDO8W5m2JohM6JYOCG6u9g0iMeDBxfRG1yUBK72/1th9tjTrO9a4YKUh83sOLgQmOLg0KAVutbC2UtZ3syg0q7uvT6mWycUXFpNZXL3sliW2vgWXIKyvfH3Ls71n0EJwBqIKYS0ZtNyFl91jC0lzdVNxfqsSWI1xDZ7No2VxZdBaXXVoaeAGrCxYnBYOr2AEHL0oxBIszcqz+5LBFQmLaxzqE8ClWd8BriZFl+UitLaM5LnXMmOcX1y/u/FnuAbD0iol0i1BC8cLP3oerkYBgqvQVBacMb7GhVta+BqXBmWYWw6DPBLoRnLclsUV4Mqsr7C4YHWZpZWD67rFNTvlN5KcaHG1AzBwB2W1ntT95q6Z3EUI6yBKWjPzYznw1CoKKwgwQeopv5Glr+NNtLoUNg41T4gbEEyuzgg+cUsr3dIkgSv7rhTM4uBqWVzYZLwvBxPvbPze72z8XiGmCXTjPlu77cCM5CqMQd83lWvkWxb0gtD1xqqwzO/p1iQJPGZxhdUV955K52lOwgjGiPyDPdGoQqyZYk0R3wkXIdah4L4cehRhlrNPLUZPR2W5FO22K7FGZ66/dV/Tio3BeLQAjbUUiJG7BWFZwYpDQl4vejuXLb2ti21kxh4wWGNwq+JO0Ig4NVch3Kjat8Lij1vsJGhhouXWloNZ3b5Z8lx1E+om4xM5PTuX8wvbZDy+rpWvYXSztgiuwpBX1WGCq9BcH96/l7caVXggWOdCgl2NKlwf6qZZdSEBXoACZtwBr7S+5QByOJkLMFyEjRtQM8BHJnhfC9Mku7rG1Vgf87OZm02BY+s/usgdWTOWPLIriyqM9asIzIhEuLF+lT/aWlW+1uRWmYMmuQFzwE18bu7KtMalrscmcS4S6KbM8BjkMtdh6yaYgFa2lockurrGlaLQsJjfZFaIjarv332QD+8/CPbi6eO79/L+7TttzzdYC4NrUaMLfZNx5CD09a3Wdgfk2dOIOV/HcTdgDiQdrNEP4C5LKZuaQI3kRoz3hlsxrYm1Q+AHGkTh0NK1pcY1iESz2OukaaxShCSsR8v+rkmANdoQFhTW6saiC3HMoaXZNjTLhmfS0IS8sOTwHeZKjQTDkTIKj3CbI1BJI2x1HdC2hKCP5WuA0Egt+tSGgFZ2V2NYzpmbcKK1den7tSa5CP/6llX1rdcKP3oerkYBgqvQVGkDMtZF9jFDx3rI+D4u/8GGfx8DvBdEE8ZtSlqZ3RHA4X5/izjMbm2iFo27z3I3mQc2WJBFE6xgg0CESnvkGdxbAbIIWU+PWQTiWDoqDWPXaC/bRK0BGrFvTOHsWTw8LVUEchj4mkhAHM+DO5YimjAedfM1Aluy93ighgZ9hDWYBjuPQFNorepADDch8u9pUIanA4o9PwqrD0dyhA2rXo4+HCnAFF4I1ICFto/1rgPZ11uXWOb3ke6BwpqPZUuPjCCwvAJeanUBOHDJBoAcWrH/yu5JZeHx7Q3GnkEj4KYpoJYE5+cbjjXiD5YWoJVgYkBJeRdxDRopif7p14FMHxpsEpkxNjUjhYbJR9g73IkAG9ascC4sK927hiwhY1BMcDdQ4ruxhQBQ28Fm/FGz1oV9gLqXTdcDLRo1ZYXRrRgOLFiSkS1j2L5VSWNtRUqnS7EowsmZMb43eJVfL/zoebgaBcptaxOW3CKHW/k/Jqrw6OiolWTX4BWbkG0228zMG4BpgIQObI37Ld16BIMyLBQfnMOlF/8n6yIG9QwkesuOBCTb9Ksbh7Ns6Jb4FVnrIwptwqOGVUd49dij7t3K9nDpBmBsDva9VhEy7yC0wIV8s7BtPrZkupYwF89jwzEedX9YykNo5zdh+Lbfq8mzaCmPNKQ7BruIJvQItNdYz4JFhdtcwMXkGRZOjk8Em1b1UQEGeMHyeitvcUsTTf3UhMjDstAMGbqJF4EKEVZuGqIOGvbt99sy68KyYgBOlgi3uetvJJSNe1QBTOmOwAgf183KcXt73O8qXIOWzikySShMsN8MiYJhKSJcXLNKeCZ7j5i8Fniys6u3M7EgDs9JiCAOzYABWO1qYAtcrZgA6AbuXfv8Q83XiAz5niU/IAlQ6oZ81MXvloDJXJZBI7KKAGTabr4Hrcl6kqd38uCa/UPNRahteNRsNAa0rq7Gowhvs6Y1bn1VMz6zogUFCK6CMMfHx4J1LrgL37xG9oXc8vJorsiUrS4Z+PsbEKT1ER3kbbYZGSvwqK9rtJdnjdDn2Z4d5PFD6DcG7HSvpchIbpkQsDnUIszinktWL0vTEyHT+WOsleARaZOi+P+eYUGTyHq2iIBhDOR4hEWCYq9Fnex/HLOw8vjfQswj1NyyUNg+KTvXbp8S0Xzt/H9ZTr5sfSe3tAAty2GH0OkTOT3BZtVTOTs9SwXHALDjoyM5ArzevJN3iDz05Lqxvwt3O9Z7bqFdI9tEuA+1jZsEumGFBaDMvYd8hXDxNWUN60Dp/6GsD9dlHRt3EZWnZUOGWC+C6w1rR3DdbV+/FYttpEbwiQeeANZeNBAFme7RTxUuboUBSAq9Pb2JJm6kmUCFrQE4F+t+KSUW+jruCA23ahTolN8luv172N+FlQZrEH0QLk30N2xY9r6GzeLaT/3aYOVpii7fxgBovcbk44NayXqrku8GZIyDqOv/hR89D1ejAMH1nab6r//+n++cwZepABWgAlSgNgXgVfsZBdd9U05govut73xSehFv7PJ30wp1+UyeSwWoABWgAg+rQIkRXY/jKm7KCYLrYduc304FqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBEoi6HsfVElx1tDlrSQWoABWoWoGugCqdDxEIrqq7AitPBagAFahDgRKIuh7H1RJcdbQ5a0kFqAAVqFqBroAqnQ8RCK6quwIrTwWoABWoQ4ESiLoex9USXHW0OWtJBagAFahaga6AKp0PEQiuqrsCK08FqAAVqEOBSSD6+9//Ll2O41z8EVx1tDlrSQWoABWoWoESoMbhhf/Hj+XvhQgEV9VdgZWnAlSACtShQA6feB6QClCN/x/n5Y+4WoKrjjZnLakAFaACVSuQwyd/nsMqnuevjz+HCARX1V2BlacCVIAK1KHAOIDy/wNYeMyPT3qOqyW46mhz1pIKUAEqULUCkyCUH7sJtHA+/giuqrsCK08FqAAVqEOBHFI/8hxXS3DV0easJRWgAlSgagV+BFb5eyECwVV1V2DlqQAVoAJ1KJDD50ee42oJrjranLWkAlSAClStwI/AKn8vRCC4qu4KrDwVoAJUoA4Fcvj8yHNcLcFVR5uzllSAClCBqhX4EVjl74UIBFfVXYGVpwJUgAr85ynwKMGFSrFQA/YB9gH2AfaBUh+4Ca4Hg8E3NzQ/yU25/DneyD8qQAWoABWgAvetAMF134rz+6gAFaACVOCHFCC4fkg+vpkKUAEqQAXuWwGC674V5/dRASpABajADylAcP2QfHwzFaACVIAK3LcCBNd9K87vowJUgApQgR9SgOD6Ifn4ZipABagAFbhvBQiu+1ac30cFqAAVoAI/pADB9UPy8c1UgApQASpw3woQXPetOL+PClCBR6XA3/72N2F5HBrctGMQXDdViudRASrwSyoAaI1GI5YH1gDtcNM/guumSvE8KkAFfkkFCK7HAW2C65f8efGiqAAVuAsFCC6C6y76FT+TClABKnBnChBcBNeddS5+MBWgAlTgLhQguAiuu+hX/EwqQAWowJ0pQHARXHfWufjBVIAKUIG7UIDgIrjuol/xM6kAFaACd6bAj4HrhTx78kSeZOXZi8cBgm+H+KPeT+X5b3ldJx3LX7/b52iHm/4xHP6mSvE8KkAFfkkFfhxcGQBePJMnT57JiwfeE/VtaAFAkyA16djdwiqvJ8H1S/68eFFUgArchQI/FVwTgXB/g38Ogm8/nwSpScfur+4E1130bn4mFaACv6QCPxVcsLiePpffwuL67bk8TW7EsMQcEC+a1+Be/O350+RyfPr8tyaTR+sznoi5In+T50/jucMl/+7We+J7cwhNglR+zD4/XKDJ/Tnxc+19z56h/pO+K//e8nOC65f8efGiqAAVuAsFfhxc2RrXsxcNcMatrxfPxICEgf5JAzh1Lz7x10Yyarkb7dw2ONw1ifOy73vxLECWA8g+rwVCherYOePHxj7brLex94xdz/XvKENqkjVIcN1F7+ZnUgEq8Esq8OPgcpCoNZJZHC3rxOGmoBkDwDjg8v/HP3M0kjag4vteyLOw9Irfm4NkvA54LTvmn9GCUfFzs/eFpXmLR4Lrl/x58aKoABW4CwV+GrhG5u5Lg/0E6Ey0XHJgjFs+Ez6jAVfzfXAzfv97c3DBFZgFleB7J3xXuC/V4pvw+uTryb/n5s8Jrrvo3fxMKkAFfkkFfia4WlaLAilzASYrZNxC+db/eC1cgBPgApg8fSbPnoblFZbTpO9tQwQAzNfj9P/M9RjuvAaKVpcEyOL1tL8nPud7jwTXL/nz4kVRASpwFwr8XHB5kEXJbdfVVZgsoVhHG7OSRh5EMQ4ctY7iPU9aa2ENQNoBGDnEbJ0t3p9BceLnjoOX4LqLfsrPpAJUgAokBX4MXLcbpBt48P2hBS2u1CX5hApQASrwbQV+BFwRLj7pMQZkPt4MzgTXt/spX6UCVIAKJAV+BFyE0s2gdBOdCK7UJfmEClABKvBtBQiunwefmwCqdA7B9e1+ylepABWgAkkBgovgSp2BT6gAFaACNShAcBFcNfRT1pEKUAEqkBQguAiu1Bn4hApQASpQgwIAF8vj0OCm/YX347qpUjyPClABKkAFHoUCBNejaAZWggpQASpABW6qAMF1U6V4HhWgAlSACjwKBQiuR9EMrAQVoAJUgArcVAGC66ZK8TwqQAWoABV4FAoQXI+iGVgJKkAFqAAVuKkCBNdNleJ5VIAKUAEq8CgUILgeRTOwElSAClABKnBTBX4IXHgzCzVgH2AfYB9gH7jvPnB0dCSl8qT0Ao+XRaM21IZ9gH2AfeDh+gDB9Q2qs2M+XMek9tSefYB9oNQHCC6Cq2iOlzoNj3NAYR9gH3jIPkBwEVwEF/sA+wD7QFV9gOBih62qwz7kLI/fTSuDfeBx9AGCi+AiuNgH2AfYB6rqAwQXO2xVHZYz3scx42U7sB0esg8QXAQXwcU+wD7APlBVHyC42GGr6rAPOcvjd9PKYB94HH2A4CK4CC72AfYB9oGq+gDBxQ5bVYetYcb75P8tCcvj0OA2/eVvf/ubsDwODUrtR3ARXATXT+4DhNbjgBbaoTTwfes4oDUajVgeWAO0Q6mdCK6fPGiVhObxx+Ebv492CHBx8Hu4wT/a4DbtTXA9XLvlvxmCi3Aqzlxu88Pme74N4Rg08x8hn9/vYBhtcJu+SnDdb1uVfhsEF8FFcN1jH4hBs/SD5PG7HxijDQiuu9f6rvozwXWPg9Ztfih8z7ctmNr0iUHzrn7Q/NzvD8bRBrfpO7S4vq/vffRBgovgosV1j30gBs37+HHzOyYPstEGBNdkfWroNwTXPQ5at/mh8D20uGoYSGqqI8FVL7CinxFcBBctrnvsAzFoxg/wUT++eCZPnjxJ5enz37Iw8Bfy7MlTef5bDIK/yfOnT+TJsxfZOfHa43qMNrjNpPBxuApd62ibp8/lt3sLTx9v94dpW4LrHget2/xQ+B5aXA8CN4XWdTA18GoPYC+ePZHmtYcZzG6qU9Xg+u25PH3yRJ69yDT+7bk8z/+/U4i12/2mmv/s8wgugosW1z32gRg0f/YP+ed+ns3oW4MjBkMdNJ/JCx0YmwHst+dPq7C0QqNog9tMCh/W4iq0y52CKgPkWLuHng/xSHDd46B1mx8K30OL694Hhhag8oELA2dYYQ6u58/kyb26qvL63O55teAqtkujAyzf5N5Nbtusrdy92LaO267HNGFx684+7/qE5d77ZQZogovgosV1j30gBs2H/NF/97sxYE2EUT7jx2Bog2Qa6LKB5bvf8YDnRhvcZlL4oBZXsV0acDW6NxbxaORtFSBTN3CAyNq0DTJ8Xv7+kYxePHNX8NjxB2pHguseB63b/FD4HlpczWA0aYC6g2PFmf0Ei+sF1lzCCruDutzBwFg1uJ4EcApatwJqol3GYZP9X2prPZ5Zb5ikKPiy995B29y0rxNcBBctrnvsAzFo3vQH+jDn5ZZVNkC2BrlsAGvN4LPzH3Bg+5Zu0Qa3mRQ+qMU1KrRL6NxqnwmTjBQBmrVd6z1Z25WOj1ti8d33/Ehw3eOgdZsfCt9Di+tbg/CdvXYNRhjs8sjBbPAbjUQDNCa6F7PB8J4Ht5I29YLLXHZYc2q5ZyOqEG0WbaDguYHF5TCc7CrM2zvasd3uJY3v+jjBRXDR4rrHPhCD5l3/sH/K57fcTmOD5YSZtwYGxMD5SCA1SYdog9tMCh/W4nJ4KJQyN17S3CwyDaZ4+kyejQfSTLK4tJ1sUhJBHQmK499DV+GvNYu+zQ+A7/nP7AMxaE4aUHksZvV3+xhtcJvf4KMA1yOeFNxXH6bFdY+z7dv8UPieXwtwMWje1w+c33MdgtEGt/ltEVzX9XyIPkZwEVx0Fd5jH4hB8yF+7PxOG3SjDQiuxwGh2/RLguseB63b/FD4Hlpct/lh8z3lQZngKmtTS78huAguWlz32Adi0KxlgPgV6xltcJtJIV2FjwN6BNc9Dlq3+aHwPbS4fkV4POQ1EVyPAz4/0gcILoKLFtc99oEYNPm4JA+twW0mhbS4Hgf0CK57HLRu80PhJItgAwAAAIZJREFUe35Ni+uhB21+/9KtJmwYMFkehwalsfFJ6QUe/7UGU7Yn25N9gH3gV+kDBBetsVvNSn+VHwCvg4M5+0B9fYDgIrgILvYB9gH2gar6AMHFDltVh+XsuL7ZMduMbfaz+wDBRXARXOwD7APsA1X1AYKLHbaqDvuzZ278PFoD7AP19YH/D2yzaLqUm0r0AAAAAElFTkSuQmCC[/img]
Вопрос по: Функция СМЕЩ (OFFSET) возвращающая динамический массив
Если по столбцу Товар какая нибудь позиция будет только в единственном числе, то на выходе эта позиция дублируется на весь массив. Как можно исправить такую ошибку?
Подскажите пожалуйста.
Работает только такая запись на объединение динамических таблиц:
=a2#:b2#
то есть, a2# и b2# можно горизонтально пристыковать.
Неожиданности граничащие с багом, например объединить две таблицы с зазором:
a2# и s2# содержат сходные таблицы, если между ними есть столбцы, то есть в шве есть еще данные (или просто пустые столбцы-ячейки), то запись =a2#:s2# создаст общую таблицу с данными шва между a2# и s2#, пустые ячейки шва заполняются нулями.
Так же запись =s2#:a2# работает не правильно, на первое место ставится то, что слева, то есть работает как =a2#:s2#
=СУММЕСЛИ(B2#;B2#;F2#)
B2# - столбец с датами, иногда повторяются
F2# - столбец с данными, которые нужно суммировать по датам напротив дат
Запись типа
=СУММЕСЛИ(ГОД(F13#);ГОД(F13#);G13#)
=СУММЕСЛИ(МЕСЯЦ(F13#)&"."&ГОД(F13#);МЕСЯЦ(F13#)&"."&ГОД(F13#);G13#)
опознается ошибкой с предложением исправить что-либо в формуле.
=ЕСЛИ(И(C49#>12;C49#<16);820;1020)
не "вытекает", отображает только первую ячейку
работает, то есть "вытекает" так:
=ЕСЛИ((C49#>12)*(C49#<16);820;1020)
Подскажите, пожалуйста, есть ли возможность расположить динамические массивы один под другим, с тем условием, что они находятся на разных листах? т.е. на листах я собираю (подготавливаю) таблицы, а затем, для расчетов мне нужна сводная. Использую динамические, потому что размеры таблиц по количеству строк всегда меняются. Может быть есть какой-то другой способ (кроме Power Q)?
Работает только такая запись на объединение динамических таблиц:
=a2#:b2#
то есть, a2# и b2# можно горизонтально пристыковать.
Условия: таблицы имеют одинаковое количество столбцов и расположены строго друг под другом (при этом количество пустых строк между таблицами не имеет значения).
=ФИЛЬТР(C2#:C17#:C27#;ИНДЕКС(C2#:C17#:C27#;;1)>0), соответственно в первом столбце изначальных таблиц буду указывать нужна строка в своде или нет, Таблицу C17# можно не рассматривать - она и так попадет.
Они же все возвращают динамический диапазон
И вот вопрос: как вернуть как было раньше? мне не нужен автоматический динамический диапазон, если я ссылаюсь на объединенные ячейки.