Календарь этапов проекта
Предположим, что нам необходимо оперативно и с наименьшими усилиями создать годовой календарь, на котором автоматически отобразить даты этапов проекта (или отпуска сотрудников, или тренинги и т.п.)
Заготовка
Начнем с заготовки:

Как видите, тут все просто:
- По строчкам - месяцы, по столбцам - дни.
- В ячейке А2 лежит год, для которого строится календарь. В ячейках A4:A15 - вспомогательные номера месяцев. И то и другое понадобится нам чуть позже для формирования дат в календаре.
- Справа от таблицы размещены названия этапов с датами начала и окончания. Можно предусмотреть заранее пустые ячейки для новых этапов, добавляемых в будущем.
Заполняем календарь датами и прячем их
Теперь давайте заполним наш календарь датами. Выделим ячейку первую ячейку C4 и введем туда функцию ДАТА (DATE), которая формирует дату из номера года, месяца и дня:
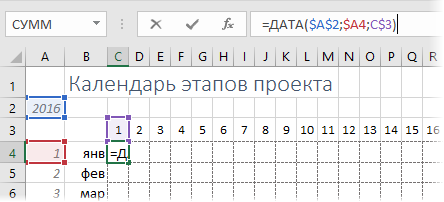
После ввода формулы, ее надо скопировать на весь диапазон c 1 января до 31 декабря (C4:AG15). Поскольку ячейки узкие, то вместо созданных дат мы увидим решетки (#). Тем не менее, при наведении мыши на любую такую ячейку во всплывающей подсказке можно увидеть ее реальное содержимое:
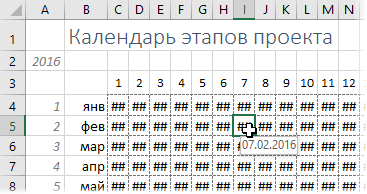
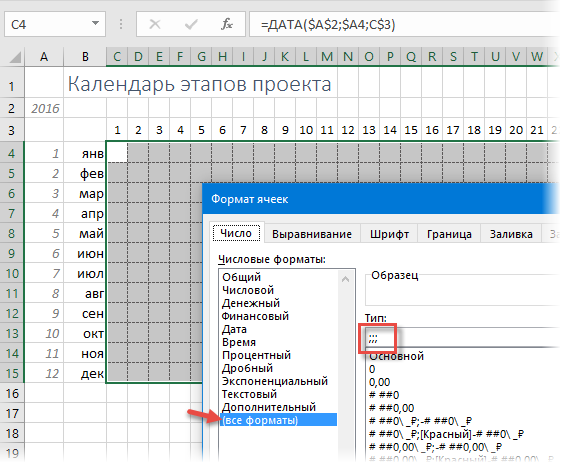
Чтобы решетки нам не мешали, их можно скрыть с помощью хитрого пользовательского формата. Для этого выделите все даты, откройте окно Формат ячейки и на вкладке Число (Number) выберите вариант Все форматы (Custom). Затем в поле Тип введите подряд три точки с запятой (без пробелов!) и нажмите ОК. Содержимое ячеек будет скрыто и решетки пропадут, хотя даты в ячейках, на самом деле, останутся - это только видимость.
Подсветка этапов
Теперь с помощью условного форматирования добавим подсветку этапов к ячейкам со скрытыми датами. Выделяем все даты в диапазоне C4:AG15 и выбираем на вкладке Главная - Условное форматирование - Создать правило (Home - Conditional formatting - Create Rule). В открывшемся окне выбираем вариант Использовать формулу для определения форматируемых ячеек (Use formula to defer which cells to format) и вводим формулу:
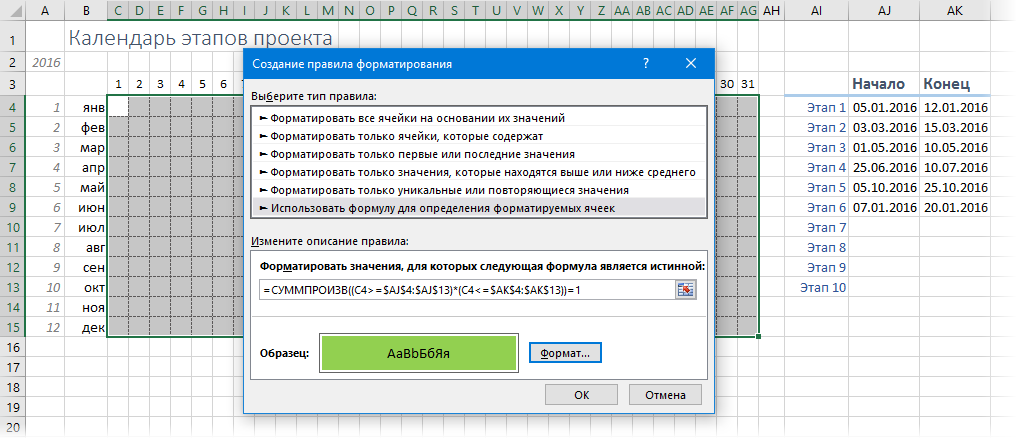
Эта формула проверяет каждую ячейку с датой, начиная с С4 и до конца года на предмет попадания в интервал между началом и концом каждого этапа. Единичка на выходе будет получаться только тогда, когда оба проверяемых условия в скобках (C4>=$AJ$4:$AJ$13) и (C4<=$AK$4:$AK$13) будут выдавать логическую ИСТИНУ, которую Excel интерпретирует как 1 (ну, а ЛОЖЬ - как 0, естественно). Также обратите особое внимание на то, что ссылки на начальную ячейку С4 относительные (без $), а на диапазоны этапов - абсолютные (с двумя $).
После нажатия на ОК мы увидим этапы в нашем календаре:

Подсветка пересечений
Если даты некоторых этапов пересекаются (внимательные читатели, должно быть, уже заметили этот момент для 1-го и 6-го этапов!), то лучше бы подсветить этот конфликт в нашем графике другим цветом с помощью еще одного правила условного форматирования. Оно, практически, один-в-один похоже на предыдущее за исключением того, что мы ищем ячейки, которые входят больше, чем в один этап:
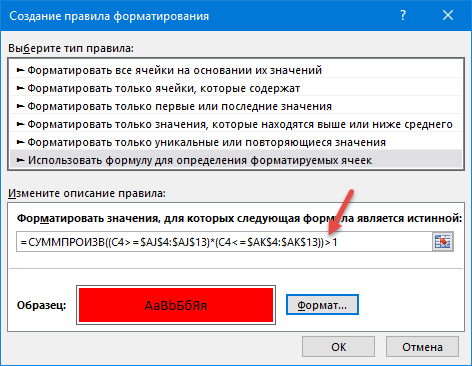
После нажатия на ОК такое правило наглядно подсветит перехлест дат в нашем календаре:
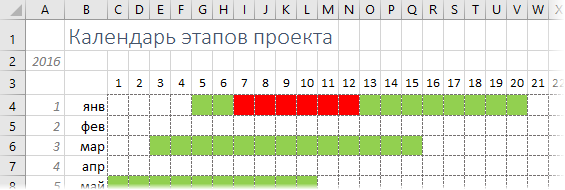
Убираем лишние дни в месяцах
Само-собой, не во всех месяцах по 31 дню, поэтому лишние дни февраля, апреля, июня и т.д. неплохо бы визуально отметить, как неактуальные. Функция ДАТА, формирующая наш календарь, в таких ячейках будет автоматически переводить дату в следующий месяц, т.е. "30 февраля" 2016 г. превратиться в 1 марта. То есть номер месяца для таких лишних ячеек будет не равен номеру месяца в столбце А. Этим и можно воспользоваться при создании правила условного форматирования для выделения таких ячеек:
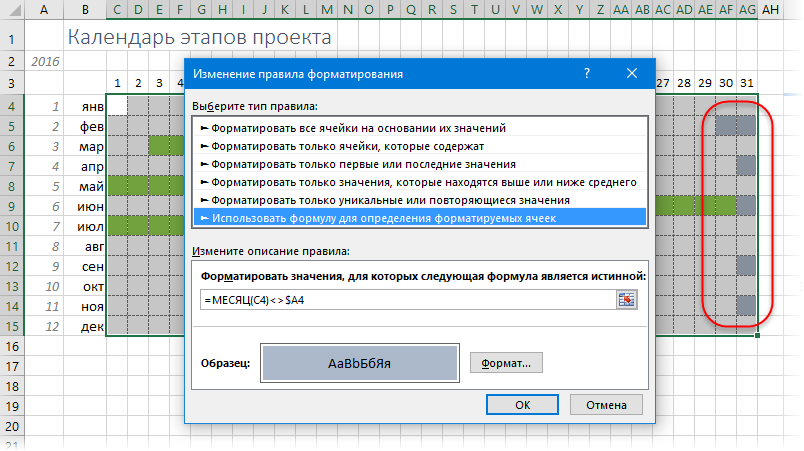
Добавляем выходные
По желанию можно добавить на наш календарь и выходные. Для этого можно воспользоваться функцией ДЕНЬНЕД (WEEKDAY), которая будет вычислять номер дня недели (1-пн, 2-вт...7-вс) для каждой даты и подсвечивать те из них, что попадают на субботы и воскресенья:
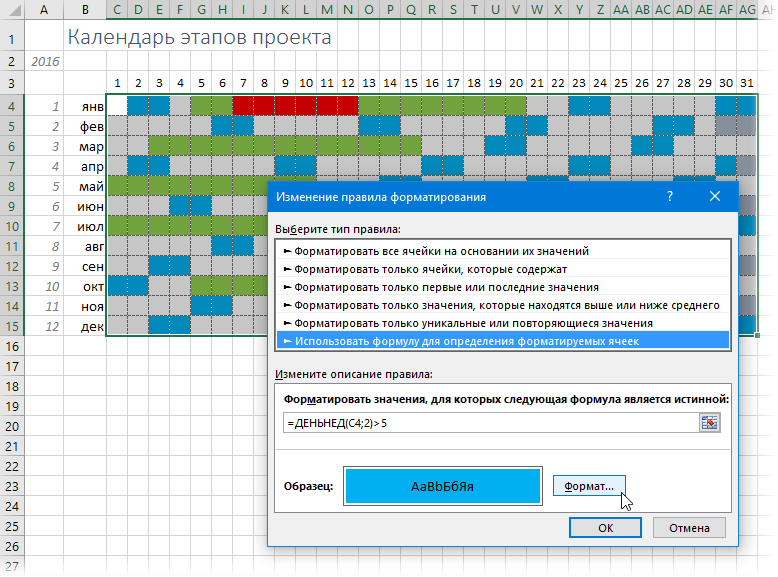
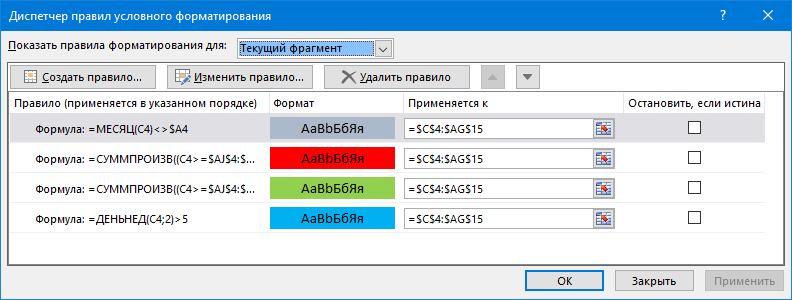
Для корректного отображения не забудьте правильно настроить правильный порядок следования друг за другом правил в окне Главная - Условное форматирование - Управление правилами (Home - Conditional formatting - Manage Rules), т.к. правила и заливки работают именно в той логической последовательности, которую вы сформируете в этом диалоге:
Ссылки по теме
- Видеоурок по использованию условного форматирования в Excel
- Как создать график проекта (диаграмму Ганта) с помощью условного форматирования
- Как создать временную шкалу проекта (project timeline) в Excel

Всем желающим в 100500-й раз мне сказать, что лучше все это делать не в Excel, а в Project - я в курсе
Project - вещь хорошая.
Но не у всех он установлен, во-первых.
А во-вторых, покупать Project, если вам нужен только календарь проекта - это как покупать целую свинью ради порции холодца.
Если вы эту свинью, конечно, честно покупаете, а не скачиваете с торрентов
Николай, можно ли как-то сделать сплывающее меню или другим образом уведомлять юзера когда курсор мышки наведен на зеленые (проектные) дни? Тогда бы ему давали информацию об имени Этапа, а в случае употребления данного примера для отпусков - фамилию сотрудника.
Иначе чуточку не информативно.
Возможно еще добавить выпадающий список , к примеру разделить обязанности сроки по отделам и датам.
Буду признателен!!!!
=СУММПРОИЗВ((C4>=$AJ$4)*(C4<=$AK$4))=1 для первого этапа, цвет зеленый например.
=СУММПРОИЗВ((C4>=$AJ$5)*(C4<=$AK$5))=1 для второго, цвет желтый и и.д.
Также обнаружила еще одну приятную вещь - не обязательно заполнять календарик формулами, можно прямо в усл. форматировании использовать вместо ссылки С4 формулу ДАТА($А$2;$А4;С$3). Получиться примерно так: =СУММПРОИЗВ((ДАТА($А$2;$А4;С$3)>=$AJ$4)*(ДАТА($А$2;$А4;С$3)<=$AK$4))=1
Форматирование все равно будет работать в пределах введенного нами периода, а мы получаем чистый от формул календарик, для ввода других данных, например отметок о прогрессе выполнения проекта))
- подсвечивалось, когда дата отгрузки(в даном случае окончания проекта) сегодня;
- когда дата отгрузки уже прошла сегодняшнюю дату, т.е. просрочено(в даному случае проект просрочен или уже не активен).
Я в курсе, за видеоурок Николая по Датам отгрузки, но там не совсем актуально для календаря. Спасибо.
Но эта проблема возникает не только конкретно с данным примером. Пытаюсь в других своих файлах ввести условное форматирование, например, для подсветки предстоящих событий по датам, иногда работает, а иногда - нет. Иногда в одном столбце срабатывает правило, а в соседнем другое правило не срабатывает. Эта проблема связана с моей версией эксель или с кривыми руками? У меня стоит лицензированная версия Microsoft office 2007
С их помощью кучу отдельных дат одним махаом отформатировал.
функции И и ИЛИ не помогали.
Но дальше шагнуть тяму не хватает:
Выодные должны высвечиваться только в периодах, и сами пероды тоже.
Спасибо.
Нашел ответ сам, посмотрев «Как не забивать гвозди микроскопом с функцией СУММПРОИЗВ».
Там я увидел, куда надо втыкать доп. Условие.
И это здорово!
Функция СУММПРОИЗВ «безразмерная»!
Втыкай условий, сколько хочешь и перемножай их.
В итоге для высвечивания выходных в этапах:
=СУММПРОИЗВ((C4>=$AJ$$4$AJ$13)*(C4<=$AK$4:$Ak$13*(ДЕНЬНЕД(C4;2)>5))=1
Очень долго искал решение проблемы по всем разноязычным форумам.
Вчера попал на эту страницу – ГОТОВО!!!
СПАСИБО!
Подскажите пожалуйста как добавить подсветку определённых дат, которые будут выписаны в столбец АО
ну короче из одной даты вычитаете другую, и получаете число с нюансом, надо ли вам включать крайние даты в длину срока (может понадобится добавить еще один день)
получилось что то вроде этого
[IMG]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABzMAAAG5CAIAAACFpI70AAAgAElEQVR4Aey9/4slV3YnGP+C/oImf2qoQo1EIaFHpRbmlwZv4sRspyh5l2pVL6m3TKYrPb022xSopcxiUZomrYdg5Wq5ukqmZpBqWtCM1upol7AKvFi4sNfZbtoau/ohmGbU00jIwqrtaXmWFW8591uce+PeGycyI168l/lRv668cePE+fK555648Xk3I4t/+C+fB58/+ZM/CXpwCAQWAYHNzc1FcAM+AAEgAASAABAAAkAACAABIAAEgAAQAAJAAAgAgbYI/J9/9+vf/tcv/+df/PLn//m//OLjT3/5yWfFn9T+u1ke1vrQQQgAmWHzYHNzsysH5jaUD155vCufnZ4+dDrl0cbc4OrWULfaosgcrXNujnVrqBNtciWQlGQXUAJKeQSQIXl89FmgBJTyCCBD8vhgHiFDkCF5BJAheXxQQ5AhpzBDIszszfKw/vlv/98X+NQRuFke1jvRMzcENjc3u7I1t6F88Mrj/+3+a91+SOd8Z+jc4OrWULfaOsR8bo51a6gTbXIlkJSkHFACSnkEkCF5fPRZoASU8gggQ/L4YB4hQ5AheQSQIXl8UEOQIacwQyLM7PsfPuCf//Djz2+Wh//1X/5ffOoIAJk6JvPs2dzc7Mrc3IbywSuP/8t//G63nwevPN4VDkI9c4OrW0PdahNiJRGbm2PdGupEm1wJJLvNJeAJPPMIIEPy+OizQAko5RFAhuTxwTxChiBD8gggQ/L4oIYgQ05MhkSY2X//lx/xj2ZmP/uv/4JPHYGb5WG9Ez1zQ2Bzc7MrW3MbygevPP7537/c7efBK493hYNQz1Hhmgr1O7GjGorXq261OSeP35ibY90a6kSbXMmxJSPpt5A6I9l7bD+h00Pg9OFZJf/pi70a+u5i7wPPPnT2ETt0EgLd5dJS4Fkl5+mLvRqg7mLvA88+dPYRO3QaBFBDJE9Ppwwl+ezoY773oVMeESQJASkz+0+f/XohPu+89pvf2H1rQZz57Nc3y8OFgOVogLyz+5s33n1599I3b9xf0ig2NzebPH/35W9c+uaN1765+9qPsyi1Hsp3dn/zG7vf3N1t1Bx4+OCVx3/9k+80f/7db6//T7/9+7//23/075qFH7zyeGBFdGhDePn91rO7NVyf3X95d/flG+++fGP35Xda5FuzoXd2v/mO8t810gPdrC19bQipwFx4SVr5kRy7/3JTVtcdEBnSob3/WmNlaNYmQMlT8s7ul/+VrfDvv/ab/+oST05P8rNf/9M7u1/+hprXNVdDyc/e/eY3dl9+R5U7nS12LGqSpFZN7Uu/6RfGmuRRdAaQ1nSS9W/SNHntLX9W1iTvv7W7+81vXCJXb7zLi1so6YagCaW3dg3yP75h51QMJSv27jfNSHl5GFr/7Nc/vnFJzdB3v7n7Lk/IuuRbu7s03E1+/tNnv/7xO6r2fiM7RsFqwT/0rPNTtdtiUvKz8OaSlLSV1t0sGiVftlnaLGnzJClZq71JSZcqtuFJ0oxjCzAro8c0J0kOVPdfT7KukI2+Jym07iusFxNPZyDsF5OkZK2YJCVrlSQp2V6nqyRJnbVKkpCMVJKEpKpOOjPtMKUkbZX4tSsmlSSD3Yp5xeSAr6uZcL2SVDr99KhXkpRkvZJUkkEpYJ5Ecp4L87YqoZVOddtiC+90DeFKagXkn4Knj5hwooawZb9V626ylZ9cYa2AeNa5pKsJrhH4GYTPxDydgZhfQHKSWqFNzmZJe4OrJP1w6gWkkgycjK1GEnhGVg6VZE1tsBqpJLmrtQLi+ZnQmaghXoYEq5HKuqfz3fpqpJLkfroRj44Rk7SVoSogVUQRMa+A/DjIOibfVEOq2JtqSCWZqyHBIiFfQ7gw8zlSbbik16ZHoQp5fspOdrcI8SV//U8x4XgNiUpG1iG8uEUeAFN+1h/omKR+VmWaXUbVKy33M19DuGS+htQl6zXEl2moIYGwvwjxx4hF3TjffbXJGsLFjqQzXkO42vw6pJLcfbn2RMPGncXuRjxaQyqFr70ce6KxOiuFVixbQ5jat2pPNFZnmJxEevhPNCnJt/wnGikz+9Gnv1qEzw++d/MHd3Z/985COPPRp7+6WR4uAixH9MEg+ee/u/vnR9QwdFZsbm7mPf+b710SZkvroXR5eGf3d7/3j3k3+Fl688CP//fmz7+98Pv/ViCmVD145XFuQtp2IbQfx7Zw/c33dic/Pcq0bTbkonCNdDjN2tLXhqgKzIWXpJUfybF/nOze/Ju0zqh1kSEKTVQWmrUJUPKU3Nn93V1T4f/me9TmaeNJfvqrj7Tw9/7xo5/eDOZgIMnSLwQtkCTQjM9//ruXPHgDySPq9IttoPOjT3+VKll1SeaqN7NCSTcETSjZwEOIwjudVvjTm2akfLWhdcpPUjjZ3f2Bn6sRSaXqBxJJqzbIf64zWC0Eh0lJN/p2pFKS9ZFKSVpgVWqpm0WzpMXq+JIsUU2eNOu0OcMlP/r0Vx6GVkbXmZykSgA3UlyyptArO1xSaD1UWCsmXGdEmBWTlCTD08yUlKQd96qSpCSPorPD/KyKnjhD7KxPRWRjr4qJkwxhv/MrKuB6pJRaJxkOeq2SJCVrlSQpWasklaRfCjy31fSsJCsAVQL7F8br56ckmashXImba2y12WS9uikcRZJZZ8kZ08kk7aC7eyjJe9bjQEWyzqrSBaHKoki1CR1I15BQsgqn8jOQqRWQSrIey656FrBTIyXJ8Kzi8lAKfKAH3lgNYWJH1BmrIRz5XH4G4VeHtdFkflrlasrb56Yq9ohkBVGFZ13MLyCVpL6NcvlsDbHuqRTK1hBPMl1DAgDzNcQT9nwO5xGX5O1gdninjMJqERKgFBfWAPqzWCjJxVh+VpPOjTuXtMDmakhcvlaTPTF/EdIUe7KGeDodpD5KoUy2hkSE2SKE+8klGZ7VBHF4hs8RLpfsE42T7EBnrIb4akMSxlkP/UzXEK6wypBYpY1JVhA5PCNi2RriyWdriCeZrSGepF9DpMzsLz5+sACfdy4//84vPtb/LoI/D26WhwsAy1Gh+OHu2vM3/vD5Zy7/8ftLGsXm5mbe8zeff+YPfyzCp/VQ/nD38g+V5h/faAXgg1ce/9X//e3mz59srP+PG7/3v369LJuFH7zyeB6H+Nkf7n75mWfWntl9UwYRV9IWrjef333z4wf3fri79swzl3/YIt+aDZHO3cvP714mzQ1j3axNXuhcAsgvSUseybH3//D5G/fSOvl4ubbIkIJUMnGatQlQ8pSQvI6L6vy9P97lbniSHz/4hVJOqVWbg4EkqwMhaIEkAfXD3bU/focKo59OgWRbndG5FuhUw/T+m88/s1Yb2ZikQcANrm6Ekm4ImlAy99aa2C8+Du50bmhco5p3oXWVn/f++Jkv0727EqvpNKco9tr9KKHTy41a7HqdoP99YJcN7pBH5EvWbovMuifJEsA4n5LUiUoeWmwzkqqa3XA1OSMZZFRKsl57U5KU+X4tZZI1DF1eqWHNSX7sTTom6eGprafneyjMp6fVWZcJi4mVjIfDi0lKko27iSslWa8kKclWOoXj/ouPw0qSsk6ZmRzNOqQq2xszWS/UrRib775CJabqPPXrgp/xM6gkGcmgkmQkk3cZrxQEbhMITKe6a7jltHdhTpKNe62GcCVudCJ4qgt94XQNCf1M5hJTWC8gXuxMsl5APEld/3352CyuReQXkFCnr3DtGe++kBkjbrrS6WuLrkYqnaHwA15AKp16UWHTgw16VRgrnb5wroYw6211Jsc9sJ6rIX4uZWoI87OqM9FM5pK1AlLhWRMLCkglWU+5jx+ka0gYUbqGhJKpGsLGpXbHqd03PWEvxrCGcEneDlZB3qmmGhIIZ2pIIJnKJS6WryFcUlJDAnk+kfk88sSyNcSTrD3+JHU6SHWa2TtCoC1fQ2rCyRrCJVk7XkOYgMpV/4nGRcTFWFukMzXuv/j4AVP1ILsOCSTJ1ehoegqdTKyGeJLpGlIXy9cQXz5XQwLJTA0JJHkNiTOz79//uXvVrH7P7M9/+c/Df/70hf/+29/7zne/9zvPvHB7Efz55T/fLA+Hh+XIUPzpC7/zpzSst7+9KHi2BXNzczN/yV9+9xkdY17s50cYSovez11DNhDEzP71/9b8ee1/+L3XBGJK1YNXHm8MMCLQ0nOuoW3mVwPxt9/7ne/+PVeVbzcbclG4RnogmrWlrw39FJgLL0krP5Jjf/+db3/vL9M6o9ZFhii0v/+OoCw0axOg5ClR8pQt36bq9JfffeE7f1vdejzJX/6zmXp/+z0S9pMqkGR67vyOD1ogSaAlfA4kj6KzlvyBzmrIaj7EJWtikVLmZATWb3/7he/4mGuXfOuUGwpGysDvfNdLQl9Sj92d3/n2ndvffoYPZcRPncnOW5bYEZ21WEI/g9VCcMgLfnDKOuBui5V1X7KqadbVlGSVUVZ5s6RcZ5Nk5acFrdl63U81L7wFmJUJka9L/tKrVFnrXtmpJOs6o9b9AdKwB8Wk0hkT/jkrJinJ+sRPSVbj3jxGrtCZAtWg0w6lN4+CiLRRBlRSZ63oJSWdNutAUlItLHkxMZKhk5FiktYZVpK0ZFjGk5I2EFd7uWS1Qg7dpspWSTIAqW5YlCI1xJf8Tm2BWunkSmybZ1Ql6et01iMRySWtRXVHsKtohlVlnUlWpm1niFLWgUpnIOYXkFCntWWRz9UQPqDBo4GxHmr756CAeNZrwryApCTZpKhWI8nYrYnIaNpT/l1brDM6miHy6g5uDXkR1SWZmCdp++0AKZ1R61yyVkAqnZ5YpIBUkn4NVPMxXUPkEQWSLJbgbljdfNUl3g1U+cbHPRCucjUr6V3lS3qnLGipGhIX1gD6tU4oycWqNsPKxV6dZcCm/Pz5L9WUVNwFoe3i8mMPxbI1pOZAsobUJPUS1/yrI6rLUI//RJOLnS1CeCZztfVFCJcMY/ch4pLH1RkbzdC6TiHmg4s9IsnEUn5WIx6zziPS7BartzRMkTGi3Ig80aT9zNWQwIHK23x+slh+/st/jjOzjpb993/5kWZmP/jw08E/rz/3/Ovajbee33preH8++PDTm+Xh4LAc3YG3nv+Nrz+/9dzzv/Hcnx1dyaCJsbm52eT5n219/etbzz2/9dx1kzwJh1sPJUPvLxI6o749eOXx/+ev/k3z58Zvrf/2b/3ev/mt/+PG/9Io/OCVx6O2GjqPMY9aw/XhT/+ARuH5ree+vvXWTxscY3g2G3JRuAa7PDDUrC19baDqA4G58JK08vaO/fR1mrnXW+WetGTp0P76emNlaHbbTpM/+OtkxfaUONNfp9D+4o+e5xd6kh9+6obg9ef+u9/4Iy+pQskP/2xL1bqtr3+dK4wDkhjZtM5G687Vn/6BP2Q1nZ++/kdqmnzd3uxsztQlKbtirtYkf/oHz6kaKNH51vNfVsgHqRvo/Is/+vqX1V3DNZx8IPnBh5++/pzG/M+2/BtNXVIe0evPff03VD35A7+YOJ3BaiE45OMenrIZ65I/pfMDSirv5pKUZDr1hG2UdHFlJINVUFKyVnuTki6dbMNJqnG0OanPWhk99GnJsFI5yTryFBErO04yal2vXvR01pJJhayYOJ1xYUpXM52TkrVikpT0IcplXaWzybrRWVWSlPV6JUlJ1uddWjIsJmlJqk68mGjJEHYq8mExSemsV5KUpDiin9YridP5AZu2dbf5aGpz1XKaXVifHVxtpoZ4Ykyhu+NXfqobQd16vYbU/UzVEM96rYB4sTPfqvsRy3zPz5qr3AFPslJ7vb7USUj+mXEgUUO8oKx+tx4wOm0/1X8dxV9f/w1WQBpjdwUkKVlN9mo10hCRXQYIdFarkSadkRoSZEimhgSS+jA+mhxSyqVwNVL56UmGBaSK3RerF5BKUuPG5DM1pEVEXhpfz9UQtkjYijEYVezkKltRMJ/JsZBtYJL8qlCSiTGF8RrC9VjheA3xJfmg+34y6/kaElWYqSFR+TB2jqcmOrzHpQzyFFGqhvim+SKExc4Cb6whvkINZryGcElq6yeFRA3hwgzJWi4xVyudiRoS0ZmoIUxyq/ZEk0S+9kTDJLmf2RrCTBPn4y9C4mMUW4QwSf3oWjmwVXuiYX7yrFOkkw9+QpKIEf5EI2Vm7/+nT/CpI3CzPKx3omduCGxubnZla25D+eCVxx+89687/rzyeFc4CPXMDa5uDXWrTYiVRGxujnVrqBNtciULK3n3B3/84g/+zg30wvrpPNQN+BkAEj0ESlFYgk6gFAASPZSgpIuJRFKbgGQU6qATKAWARA+BUhSWoHPBUXKrkQX306EKPx0UmQZQyoDjTgElB0Wm0YgSasj9//RJI0oO4c4lI8zsf/jx58HnZnn4/gcf41NHAMjUMZlnz+bmZlfm5jaUD155/LP/63/u9vPglce7wkGoZ25wdWuoW21CrCRic3OsW0OdaJMrgWS3uQQ8gWceAWRIHh99FigBpTwCyJA8PphHyBBkSB4BZEgeH9QQZMiJyZAIM3uzPMQHCCwFApubm0vhJ3eS9sz28OEm0AYCQAAIAAEgAASAABAAAkAACAABIAAEgAAQWHwEIszsh598Hnxulofv3b2GTx2BoijqneiZGwKbm5td2cJQdoUk9AABIAAEgAAQAAJAAAgAASAABIAAEAACQAAISBAAM3ssxhl0niTJ+pMBM9sfttAMBIAAEAACQAAIAAEgAASAABAAAkAACAABINArAmBmwcweC4Fes7NROZjZRoggAASAABAAAkAACAABIAAEgAAQAAJAAAgAASCwmAiAmT0WL4k9s8OmNZjZYfGHdSAABIAAEAACQAAIAAEgAASAABAAAkAACACBIyMAZvaUMbP7q2fPrJzd2n7v7t7O2srZM6s7twiBg60V6l/bPnImDXJhxcze2lhf275999p7+6tVdGsbB/R+5G2KdG3j4Nb2ugr54Na19/Y3dvbVqa097TlI9kFGEEaBABAAAkAACAABIAAEgAAQAAJAAAgAASBwahEAM3vqmNl1YiSv3d7SnOzeztrGbWJpN27f3V5fXmaWGGeK6GBrdX1t44Ci27t9a2N9a89Geu321sbOLRv4/qrCYXsHzCz+uB8QAAJAAAgAASAABIAAEAACQAAIAAEgAASAwBAIgJk9pczswdqq2k/KOdklZmaJft3fWN/a2NnaO9ja2FnTzOze7bvXbKTX3qN9tfoUba0FM3tqv49C4EAACAABIAAEgAAQAAJAAAgAASAABIAAEFgEBCLM7OUf/ezDTz7nn5vl4SL4uoA+LN+vwBtGkn6d/+zaxs7W6vr+9oH6HX/1m/4r+uUGCwh11CX3NoPbWxsHd/d2zpD/RMUqEpYo2v09er8BEbIb62eIjDZbaNUe2+rlBnevLd9QDvFNTnQU0AkEgAAQAAJAAAgAASAABIAAEAACQAAIAAEgcAQEIsws52R1G8xsCtkTQeft7dBrZ9Xe4Vv67avH2kecwqqPfsfMHl35Pr3i4D0ws+B5gQAQAAJAAAgAASAABIAAEAACQAAIAAEgAATmiwCY2WOxkCeCmT0WAkenRLtI9A6YWesGhnLYoYR1IAAEgAAQAAJAAAgAASAABIAAEAACQAAInDYEIszszfKw/jltuAjjLfDfoAhsbm52aF846BADAkAACAABIAAEgAAQAAJAAAgAASAABIAAEAACx0cgwszibQbHhxUa5oNAh3tm5+MwrAABIAAEgAAQAAJAAAgAASAABIAAEAACQAAIAAGNAJjZJf5dfiQxmFnkABAAAkAACAABIAAEgAAQAAJAAAgAASAABIDAkiIAZvb0MrO37StWlzR337t7Dczs8o4dPAcCQAAIAAEgAASAABAAAkAACAABIAAEgMApRyDCzB785PPghQY3y8NTDtMJCP/2/sb61sb6mZWdW9fe2984u7ZxsLa6vn/N67+7t7O2cnZrb1nibWZm91fPrq2ur60e3Dq9FPyyjCb8BAJAAAgAASAABIAAEAACQAAIAAEgAASAwKlCIMLMXv4RmNmTy+LtExt7sLZ6QBtmt9fXtk26q35q39pYP1HM7AYx0cu/OxghAAEgAASAABAAAkAACAABIAAEgAAQAAJAAAicMAQizOz3PwEze1K5vL0dxclaZnZvZ21DvdPA9FNynzBm9tbewf72ztrK+v5JHVPEBQSAABAAAkAACAABIAAEgAAQAAJAAAgAASCwlAhEmNngVQYffvI53mZwMvj4g7VVvYHUMrNmz6zrP4HMrN4te2vjrNsdjP2zQAAIAAEgAASAABAAAkAACAABIAAEgAAQAAJAYAEQiDCzl3/0s4CcBTN7ApjZ21srZ8/QG1fX9/f0e2Z31lZ29q95/be219eU2P5yvGq28T2zt7dWd+jtuoaSPgHjiBCAABAAAkAACAABIAAEgAAQAAJAAAgAASAABE4GAhFmNqBlsWf2ZIz0iYyikZk9kVEjKCAABIAAEAACQAAIAAEgAASAABAAAkAACACBE4AAmNmlfAnFCci8TkIAM9sJjFACBIAAEAACQAAIAAEgAASAABAAAkAACAABIDB/BCLM7M3ysP6Zv2ewCAQaEQAz2wgRBIAAEAACQAAIAAEgAASAABAAAkAACAABIAAEFhOBCDOLtxks5lDBqzoCYGbrmKAHCAABIAAEgAAQAAJAAAgAASAABIAAEAACQGApEAAzi7cZLDECYGaXosrASSAABIAAEAACQAAIAAEgAASAABAAAkAACACBOgJgZpeYl6wP52nrATN72kYc8QIBIAAEgAAQAAJAAAgAASAABIAAEAACQODEIABmFszsEiMAZvbEVCIEAgSAABAAAkAACAABIAAEgAAQAAJAAAgAgdOGAJjZJeYlFyFZb9/aPri1N5QnYGaHQh52gQAQmDMChflv9eCu/La1t3OmKM5s3G5xiVw5JOsIEODr+9fe218F7HOeIDAHBIAAEAACQAAIAAEgAASWFAEws/UnK/TIELi1sb62cbC/N+AzP5jZJa07cBsIAIG2CBDf15pgBTN7BNCOdcntrRVNoZ/dGuw7y/Z5cqyQYQ4IAAEgAASAABAAAkAACACB4yCwsMzs3m3aibl3+xYeGK69d3d7Z23l7NrGAZGh28SE7q+e3dp+7+6e6aeejR3ap7Oxc8v+Wz97d3tna9tI3t1eDzSYZ35ta/Xs2srZMytnz2wcaD1nVknz3WsHqn99f+/21ur61sbOlrVIrMH2ztbee/sb68rbOTC2YGaPM/lxLRAAAkuEQMXMqv2YO2uaANRbaLfX7Zbaaqvm/qrrK4rCEIW3Ns4WalPn3WuKQ1yhwl51kp6AUjwwhvTeW0X1Or1nNm77Vtb3PS6YrlU7di1fmTTnWzEuaTvDj5GJ0e1WNmhXI9LEmNvwi6LQShyMBEjtrNpya4dp+PCbooOHQAAIAAEgAASAABAAAkAACBwHgQgze/CTzz/8xPvcLA+PY+No1x5sra6vGTbwaBpOzFW3tywO+6tnFUOqwNk4oP6927c21okPXVW/QWl5UnrYC87u3b61vb62rSWJYF3b9mTU01dliwhZ+h1Y26MP1b/KotevrWtmlvQQb6uZ3F5HAcxsr/BCORAAAouDQMUDKqKQ+FPFqHpEquNYlUzFk7p+v1EUPlVKV6keR8a5Hm7LKVFfEwZKKsL3ruV5jTP07R3dg9zlTrlrOCvU0J5sDz8Eyr2z+jUFOuQzK4bgVqEpBllRrnSoGi5GhyQ1DCAEkSKsiY9ecwEyuNY2zFsRvMvxRTUQAAJAAAgAASAABIAAEAACJxCBCDN7+UceLfvhJ58bZpbvykzsozRPUPsbtN1ybUO9Dk/t67Q7LrXAwZbaj0ksodrpqfdyxvZ4qn2dJxD3Vo+aB2tmqw7Rnfsbaqfq3sHWxg4x17S5WO+iDZjZA//s2a3tg/2NswpzRXnTE7Ino54AnS21IZeYWdujmVnzXL2+5bhX1c+YWdpLu7992/T0O3ZgZlslEoSBABBYXgR8ZtawlrRVlqg9tweTSML1/Wt2s6rbwaoaFStqdn0GpKq9qqrbrMdquMv32OrdnT69a9lVR9GqhrmLEf6WtXTKXcMEYv1cpD2zqzuGTiUczm5trHt7WqlT3YI1M6uw8gQUpJZupngVIesoWguLo8WtQjCzQAAIAAEgAASAABAAAkAACJx0BCLM7Pf9DbOMmV2lDTjZfZTq/QP0++w76rfdd/aDHZf6eY9xfMTfmb2capeltwNU7+tc3gfpzjzfXz27trGjPvRugTP08EaEqX7T6xahTe83OLO6ToS4/neb9tKubRCBq86qp3qzZ1btsbIcq5PRuW5tHdwyY/0e8bkbO4pvVUwuPVfTLl2lX/Vb6/Sig9WdNfWWgzMrFY/Q2ywCM9tZjvU2RvAQCACBThCoKqrbYar2YBb02w8rwVZNy3UqipC2Z6oGZzzNiwgqUrXa+MmqgdVDvwlBf0xMb/C01CrF5Zxhneqq1XX7x8cq97RmJcnNRaxYEvO9u25LacUXd4JnCyVmJ+z2erGys79xlnbFErVNI1LFot4CoSTXiXitbXoN8HHMbB1SQgnM7HDDzfK/RZLgKiAABIAAEAACQAAIAAEgcFQEIszs5es/i7/NQL3bdF0xs6l9lAEzq3bu6J0yluYjRxUnqP9VOvVeTm//Jr2rdHVH//b9UWM7zUvqg62B/hi3ftHtvIYMzOxpTnLEDgROFQI+M6t4QEv2VdQnMYNu82ZRvc3A9RsmURGy1Fkxs+v0TepK8DaDqsfaIsx5u6aEBJQ54wlnb/23GTjlrlFpJhPKtwViZtVOZLNJ2TCzB2v6tbxEpNJXnjpwS4VXQ+aYXHVzpHjt2wzMF6XhBlsws2BmgQAQAAJAAAgAASAABIDAaUEgwswm3zOrfz/d/JvYR6kpOfqNe/pDUvRYUrqerkUAACAASURBVO241H+neE/9CalV+iNRZ1bUjkvL1fp7PKt9nfOi+U7VQ/7JCBbM7MkYR0QBBIBAIwIVzafI0LNn1K5TRfDpF5iq4xX3OlRFd6o+9Y+5vIFUVW850Ls47Z2XNrTq/1x/gxLzQlX7165oOWWVeESwcVuptQLetlxtthGZ3gUIcPUds0JevULd7pnVVKxy1DKzmlD2qFVvLChehTNdRWrDs0wnewvtaVmV9j6aNrFhCAgAASAABIAAEAACQAAILAgCEWY22DBbvc2gm+Xs3s6W/eXEW/ols3jeAAJHRADM7ILUEbgBBIDA/BCo+MHGykn8oN6eOT/3aKkQYXjn60AjMhAAAkAACAABIAAETgcCtzbWz6zQu/i6YTNOB2jACggAgfkiMH9mFrUMCHSGAJhZrDCAABA4dQgsPjOrdn1Wm3znu6w5dfkAeIEAEAACQAAIAIE0Are3Vtb3t3fOsD9GmhbGKgIIAAEgMAgCYGY7YwkHGb9TbhTM7ClPAIQPBIAAEAACQOB0IqBf94F/gQAQAAJAgCMQ3BFu76tXLG55zCyXRxsIAAEgsAgIRJjZm+Vh/RPUOBwCgUVAAMzsIowCfAACQAAIAAEgAATmjMAiPEXAByAABIDAoiEQlOKDrdX1NfXZ2r5tt8oums/wBwgAASAQYWZ7fs8s9qgCgc4QADMbLD5wCASAABAAAkAACJwGBPQzzGmIFDECASAABCQIRKvi7a3Vs+rEWfeHTO9ei0pKTEAGCAABINATAmBmO2MJexohqM0gAGY2Aw5OAQEgAASAABAAAicVATALJ3VkERcQAAJHQyBWFfd2zqzu3FJ/m5S9ZzYmCU4ACAABIDAkAmBmh0T/aHcdXOUQADProEADCAABIAAEgAAQOD0IgFk4PWONSIEAEJAgEK2Kt7dWzq5tH2ytnj2zurO/fUAsLfbMggABAkBg4RAAMysckj3J/WB5ZPZ21lbOblFQt/c31rc21s+sqK8ThWgsihiY2eVJuUXJGSAGBIAAEAACQOAEIBDlIE5AXAgBCAABIHA0BKJVsXrPrHrbrH7gjUoezSiuOpUInDBqCM/pC4FAhJk9+Mnnwatmb5aHp3LKmRFS3OX2juEuK05zuTG5tbGumFkTxf7q+v5CZGQrVMHMtoILwkAACAABIAAEgMDJQADMwskYxyWI4tbG2aI4e6YoitUD+weUlsBtuHr6EIhXxVvbB/v6sxf8BTCkMRA4AgJEDZ0pzp7Z2NkHP7t89NERRnxul4CZlebT7S3LXQac5pLe9rwo9nbWlnKxBWZ2bpUChoAAEAACQAAIAIHFQSDOQSzpohRuLzAC9MvgtJlje10xs/RAtLX33q3t9bWNg/3Vs2dWzp5Z2dm/9t7+hmrTOz1JZo1OrW/tGfkFDnBxJjU8OSYCsaq4t3Nm5ezaytkzq2fPbICZPSbCuFy/HGNnrVjf2t45U6idbdvrVAZV6WMlkZdBXh7fu7t3QAlJL9lAeURGcQTAzEqY2T31bpoN80Wxx2lKLl9IGRbFwZp+M/pC+pldyYGZ5ZMZbSAABIAAEAACQOCUIBDjIJZvIXdKBmvJw9S8g9kzq4iJDfNktLWyvr93oP6lN6TdovZZYmOJdHiPNtuu7mytFGdWicZV7/dccigwxRYagVhVpL8AdkCPvds7a9W7+2KSCx0aJs6CIHCwRmys/ld/a0Xtrb3b+6sFMa1VSeRl8ICVR/Mtl5VHeVyQkV0ENyLM7NoLd//qE++FBqf8bQZmnByV6RpZ0nARRjfpA33RTd/trO+rxRMtmKidlF/USMHMLt2QwWEgAASAABAAAkDg+AiAWTg+htAgQuDWhtps6PbMaqZ1pTizoXjY7YOtlWJtm3aBrRH5ZZhZu812h7jabaIt2I5Fkd1FffqA8wuLQLwqqr/6Rfm5te08j0si5YBAIwJmV2xxdm31bEFc/8FacXZLvS7jluJVtkxJ1Lyt5mGJeLHlkb6yOrPhmFyURzcr0Ygws3jPbJAWap+5/RtZjNMMxHA4fwTAzM4fc1gEAkAACAABIAAEBkcAzMLgQ3BKHFC8A3+bgXq5gSIXiJk9s0q/ybuldstSu9DMbFGs0Ntp1SYy2hSm+k8JYghzKATiVfHWxs7+9oG/CSku2cjKQQAIEAJ7as+s3dOmuNr1Nf3ylqok3t5acWXQlkricHfOrNA7EPieWZRH5JVCIMLMBn/+68NPPsee2aFuMLCbRwDMbB4fnAUCQAAIAAEgAAROJAJgFk7ksJ6MoOxmMfx6OBCYKwKxqkh/TEVv3KbXGlgCKCY5V1dPxkxHFBkEUAYz4OBUFAEws6jCS4wAmNnorEYnEAACQAAIAAEgcLIR0MwC/gUCQAAIAAGOgF/5NTO7qv5eU8jM8qvQBgJAAAgMi0CEmb1ZHtY/X3x0Hx8gsGgIbG5uLppLp8cff92zxPw+AgECQAAIAAEgsHQIDPv8AOtAAAgAgcVEICjmt/c36O+prBE5e9vfM7uY/sMrIAAETicCEWY2+jaD08M3IdIlQgDM7ICDNZvLf3/3D7/o0E632pbRsW4R6ESbXAkkJSkHlIBSHgFkSB4ffXZYlAJaIXWon1sk4cxms2EjgnXJMAEloJRHABmSx2c2m+mq6NfMPfqrdGf0J9wz26jQ6YRkHgH5/QiSeST1WaB0OlECM4u9wEuMAJhZMLOSwu1k5Itad8l8GnNzrFtDnWiTK4GkJBuBElDKI4AMyeOjzw6Lkk8rJH8lRf7kBmZWMuhACSg1IjBsZYD1xgHSVbFWQvdu76+e3dq+fasqp/L6CclG2MFfF0UBlPIIYB7l8dFnwcwuGC9578qzFy/Yz5X7H93/4vUrT1y8fv+j+/evXnj26p0vPrp///Urz5575Ilzj+hDw80FYkzPS/coRnXVhbcHfCvFvevG7dcpii8+uvP2RRWFPgzPihwGMwtmVlLmnIx8UesumU9jbo51a6gTbXIlkJRkI1ACSnkEkCF5fPTZYVGq0QoVm8BPyZ9zwDlKBh0oAaVGBIatDLDeOEC6KvI6+d7da7f3tw+2Vs6ubRzs7wVvM2hUCM4RnGNjksjvxZBsBPOUzzgwswvGzL5+oTh35e17d+6/fuWJQhGpquf+R3deOlc8+/r9L16/UBSPvHTvzv17158tiicUV0v0XF1M67mnaNDXLzxx8RGjMEfO3rn/+h2igz+6/wWZUB91aNpam/5XyWiO9b7pqa7VGt52kooafvsesbGFiuv+1UeKi9fv37vyLIVDPCw/+0XCYeWGHjJylTGzxlvlz4KNaQ7wJXZVUluPLyNfhkpsdatNYlEoMzfHujXUiTa5EkhK0gkoAaU8AsiQPD767LAoBbRC6lD+jAfOUTLoQAkoNSIwbGWA9cYBijKzB1vqJbP0qtnwPbONCk85TyS/y0ASuZRHABmSx0efjTCz3//J58GrZm+WhyC85oSAIVjvf3GPM7MXXrr4SHGOttC+fbEoLl7Xzmhy0zhGF1Ziiqi98NLr1ytu1ClMEYWK83324oUniCq9/tK5R9QUeuTZ1++QoXOPqFPEDr99UTHCWqG5ijbwGn9UCG9fvfAEbf41bjv0lCoTiKKVLeOs+V8ypHYKE+1rEbAO07VF8cS5C29fJXr62YsXNjc39Y5gcunchSfOMaraXuVMo9EtApL6cnwZ+TJUYqtbbRKLQpm5OdatoTbappPxaDSZzmazaTkZT9xR/u2H1VVNz8yQJGyBUnrGIUOQIUtTbVJUbNDf8JwzLcejohiXzZUBkkAp/yZiZAgyZEkyRFfFoFRGD+X1E5LJlRWrDEAJKEUQQIaoe4d8dkSY2YCW/fCTz8HMdktp5bRFmVliIStm1u2TNUyopiAtQ2qYTU3U0nsPLFkZITrptQkvmXcLWL5Vkb8BZ2oNWRZVO/n6heLidcPSVrzqI8+ee4T29n505+3XrzhC2YRMPtAO2S9iVhQVa86SfMRh2mbLrr2/ubnJXeXO5EAGadsFApH620NXG+6v2Xy32prtiSXm5li3htppm07Gipk1qJRj/aTToIRdBclkQgElBQ0yBBkSQWAJZ0eUR6h3Nq31p9NyLGNmISnhr4ESUMp+uzNFhgyfIboqsmq5va67zL/ivwDGRlNeaSEZuQXrLuApYuiqGoJcOp25FGFmL/8Ie2aH+x3zKDNL20gNK+r2nH6hehxLG32bgXo7rWEz60TnFx9VLyvgdKflNy0PS6+41Upcz/Vni0eeUG9XsMKEmBK7Qu8rsIwtvZOh2gNLr19QpC1nZkkVcbXq5QzubDtm1nK43Bkws30jkKyYnZ5ooFpa2upWW0vjOfG5OdatoXbaGD8ym00nhpjNPufQDtuKz20wB0mVYkApOdOQIciQf/hFMj0WqdowWiH+hlkt0PDkNpvNhMwsJCU7IoESUMrvG0WGLECG6KrISuj2+tr2e3f3ds5UnGzb+imvtJDM3WHt/QgoAaU4AsiQ2SzCzK69cDfYNos9s32TXJX+JDPr0aP0S/1F8cRF+4v/1XtmrRhtoS2eOFeol9LSW2hVu6A3Hqgtq5VFt32S+E11ybkr6g+FOR7W6rTssKZx9etiFeFLNfYJ9zYDtTFWbfKlP/Dl3k5A72Ew/2kqVpmjKMw2WO9szGFLEOvttOTq5ubm28ore62N1wWFRm8IxKtq170NNFNLc91qa2k8Jz43x7o11E4b48XKcbV9tkEJuwqSyRwCSgoaZAgyJILAEs4ORiuAmfWH1D65Nb25Bay0YPcimMQFYBKRyf4M94/az3f9PMhK6PZ6sbK+tnr2zMrZMyvrW23eM2uta52+Z/4RJGczoOTnhH+EDEGGFIWfE/6RzZAIM3uA98z2RmZF+NDltFWRpIP6r/4C2J2Xzqk/lUae3HnpHHsfwqC+nZixTgXiV5S+jhqolpZmu9XW0nhOfG6OdWuohbZpOR6PRqPxuJxOJ6oxpnbDMwm7CpLJBAJKKq+QIciQCALLOTsYrXAMZla9ZrYoipGin3LlGpJAKb8bFBmCDFmSDKkxs9feu7W9s7VxcEs11jYO7pqi2sAkspyHZOTeqruAkqoMyBBkSASBI82OCDMbbJjFe2ZTzNQp7r/z9tX03ts58qGKmb1///U7963R+69fd+1TPEDzeB1HpAb10JV7mGxvrltt7e0nr5ibY90a6kSbXAkkkwnETgAlBkayCZSS0LATQImBkWz2gVI3zKzvch9+QqePcfwIKMVx8XuBko9H/AgoxXFhvRFm1lKxQV1tYNNqOllHsgmdSWjYCaDEwEg2gVISGnbi5KEEZnYeHBYowp4Q0MxsT8qhNo8AK4w9NuXLUIkT3WqTWBTKzM2xbg11ok2uBJKSdAJKQCmPADIkj48+OyxKAYOQOpQ/kzTsKPcRGTZ2WPdHI34ElOK4+L1AyccjfnTCUNJVMVUzeb+8fkIynjp+L1Dy8YgfAaU4Ln7vaUYpwszeLA/rH40R/gUCC4XA5ubmQvkDZ4AAEAACQAAIAAEgcFwEZkXR+DmuDVwPBIAAEDiJCDQWT/Na1JMYO2ICAkBgaRGIMLPRtxl8/NkH+NQRKIqi3omeuSGwubnZla2CXsw8j08fhvrQmUejKIr7116Zw6dbQ91q6zD8oii+9tL7c/h0a6gTbXT3fFX26UfS/6Y2eaRmWfIsP9GTZDNNox9FgJLwkUwiph7e+OBm2j2Ne8YiP9XKeotcAkqNCBD0sk/+7z+w4aSqKNY5bP1cFusM3VyzHfLiMcqZZOdazWJ2Xa7Zk84W+QmUGhFoM99zg83O9TTuzEKu2cp6H7kk15kLg51rFRG7LtfsSac8drlkLgx2rqeImIVcs5V1eexyyZxz7FwrP9l1uWZPOuWxyyVzYbBzrZ4N2XW55lKgBGb2WIwzmNmuiNGj6QEzq/lTVWvmQSs7unZuFGe3hrrVBmYWzGx0CTD8vb8Hpjsaab2zp9jrhqI9YFWisASdQCkAJHo4OEry55xl4UaH9TM6yvXOwce97lK0B5U2CkvQCZQCQKKHJxIlef2MYlLvHBylukvRHlSwKCxBJ1AKAIkeDo6SfM0Q9b/e2dMsllcbieSxmNl7b954gz7v3jutO2rTzOy7b7z4XPewHN64d0hU8j0Z5maADt89Gu+5+FdZZvZdm4o33lD4KM/ffePFpy8+9ujVN33y/ZAyto6hmq6K3JwW02kxmxbltCOuc1qMJ0U5KSZKYWVoRlbI1qyYlsX0GDt2PZ11PZ1HpPaRGV5yb+vO3iv393av7+12w1Tufe3Cxtb1jfNX9mhPbsWlakPXdu9s79456nbdSptQQ+fRJexWFOeVa1+98v7XrpTnr5TdbKG98q2V9Wvn1596+ArtyQ0NvVR+9dnyq0fdrmu0Hc9nuvf3wCTKddZv3tN614ySvt49T0nJHZ1k+sGzHnu0J4rSkSQraFvpbIFS4z4mLRAb9yNFNHMhtYooast1Hk3nIqPkQusQJblOjudcUHIGnY/UaPdENGj9lFfaYSU9fNUBh9612yE/9xriomiaHS6g+J3L6eGNJp2V7CAouZBa+Vk5HWv1odPZGQQlbt21843B8eyj0sp11sFxWcFPRVE6kmR1UXc6K0/nlnVVGLOGtQ2XdI5GY3dnZ006uaRrN+rkkvIMkUs6/flGKz/zqtzZRp1uFBoluU557HJJpz/foEwWr23yqtzZVrG7q/KNzmdchJn9/o9+FrzQ4GZ5GCPp3r362NNXD29cfezpNxQzS+yYIwEP371n2gEtqA9NJ7/k3puKdlQXKk4zuNDn1xaDC44zs4fPnXvs0XNFce6xRy8SLah4Q82oat7QR8YQuDXEdP+9wwrVey8qhW8+XRQWc0/hB4HwuUs37tEAPXr18IOPK2ArJBX+5jDE//DdN/SIEBFc+RDLhErhnM9aZpY8vPrYoxdfvHHv0KBNWL34riayuVf3Xny0KB69ekjZ+8ZnN65eevrii5RparoqknRSjMuiHNO/ZovotCjLikINGVvFe9Z51WlZcbvUttyrM0SErLI1mxXjoigVPxsor5RYDlfTuIEY1+m2tbqGtuIiqnT6HG6q3+nhDUdx3tlYubD9yvXV4sK2fbnB3u71bUXXXnvlzvZWyNju7d7Z09SqZnINn6sktYZdalv6NTB0/9rWheL8deJnt64r6tbSwaxHmdD9gQNOm73K+pwgTIPomLak80pza5LaEaZfXf/KyrPvnx8VK8/alxtcKc8/q+jal97/6rPXQsb2SvnVK5pa1Uyu4XOVpNZQUtvSr4Ghr710baV46jzxs9fOK+rW0sGsR5nQ/YEDWlvgM5NJuqS0GVfDu+/lonhSfS6ru/KTRfGUvT0H92kueVmJrRTFVSXcRtK76ZaT0XhSjsfjUnVPJ6NiNFErmvCOziXL8WhM/5WNkjMSnZRlqUQzOqfkxHg8Ho2UK+G9vyyoalDhUJ9xUUxUo87MBihxbAOUXlWwa7T5Va8q4x5M08l4ZHCZ8XadBajOTsvJeFJdF8bO9CjJcmItZCTJKX+MwtWhRmZmURoXxVT9njgp9T9OclYUIwuspsgSsdfHyBNkEc1USpUTkyK5iJTkZDyaqAwMJD0MeQbWvjnwJLknddavVMkzUsjwts4ljhI/y9s1lHzr4RhxlDzJ7DzyJLPziEvmx4hL1sfIyxAeL599jSi5eRpHyeV5NVOOxcwGM7f/+uk9OwXWr1LpENVkXZcaq/erRbFSFJfVR9WlpHXnyZPmjsCzbsbnTm1uhuPuRjA/7jNVkCeqqtQkPevefAzHPSXp5WptvtMcszVZSbq8orRL6aR+v34mJWtz00OJx16rn0lJh9LY1OSM9fG4XJz6yf3k48LbkVkc1JCJutFE70dccqYqc1HduVLWVVFMrkN833LrEC55nPqZ8XM8Lvk9zssQHrvLkNJkSFIyyMD6/Z3fyHg7mB28MrA5pUeTR8RrCEdMIJmem5717Nzkkvm5GWDor21CPOu1Ljo3feu5uVmT5OPu4cnR5ldlax2vexHkmc76GHmx8/zhGVi/v3PJ7Nz0fKuNUTL27NqG68zPTS5ZX9skrdfWnx5KHJkgr4IZxyUDxPwZx8eFt0395Mwsf8rj7doTSqAnc4/zJLNj5EnWxqgZJTuPGiTVc1yEmQ1o2Q8/+TzBzN64SPygZrg+uPfio+devHH1kuYib1x87OmLjxUX37T9jz39xptPE1GouEX3r7vkjUtEq11988a9N587R4Tvu0pm0XfjRpnZNy5Z4o8o2ufeeJM+Fx97+ipxgk+/cXjjYlGce9EEePUxan/8mYfYxTff1f0EC3GOlocl9G5cfOzRc6pHkYyVwkBYuUGcqR4aC6zWplh10vau5m1j+D99lc6S226YOMW5CG3HzH782Qc63nsW7YuXinOXnrtoyPGKO6a8uvR0cek5HdrFNz944xLBqxavhpkdjYrRqNrEOp0Uk7KYjIrJpBhNigknbWfF2PZrApT/S5dMDf2qCB7S7wxpZnY0KsZj4gEmir0dK9PlTJmzPaWyMh4RWTyN+cB1cv5Ut+kSGxG/nLuq29xh3VPXpnscxXlnY+WRlZVHVr7m9rHe2Th/ZXv3ysr5Kxsrj2xsXVkl6tYyoVsXTP+uJj3Zv7tXVlau7L2ienavrBSPbBC/6Rs6f2F15ZHi/JXtr13f/toFskssLdkyPeevXyMTF1aIKSbffAecNuuPcyze4NFxbcxt57BzXvfEFabscsL0oS995aEvfcvtY/3q+lMPP1s+/KWnHl7/ykPr1x4eEXVr+dNrK6a/1PQo+7d8+EtfefjK+6qnfPhLxUPrxIT6hp5aGX3loeKph5/91vlnv7VCdomlJVum56nzL5GJlS8RU/zVmgOOmXU+cxnmjHPDuaR7zDZe7+laP0hrlvBV9VSfYmYDyVfTT+x1yaeqZ3u+RikNJat/TifjCdGJMb7VkywnWkarUvOx0solSaP75rq24uSS+nonrwoHYxL1bd6teDQ/q0mBgG/lsfN2ndfgaNckq3gCz9SzvYsqiJ1kXQz6Qhtko+SUeEy6JisZjpG37tHrZseV6Gdg/VRGSv3PVBGUM/WvL6kdr/71I3JHGT9NLDaZMpIWHvMzIjmb0Tq71P/YgyhK1UlvFMJc0jjoFAradZQ0x62fkzVW9pm5wse1TBDhGLnzVUNLZueREVaSDnPdmUFJCzj5jGR9jMIMcbHz2Rd9cnPI1CSrkG3L5TmfKfExCjJWH2bmO5/R9fkezPGj1s9c9da8cJRv5dYvW/ZWP4ZlInpKLKlVOXn/adAkpppDDePOR5C3o+PuakhN0o62/eky0q+QkfzkkmxGN0q6vMpKknZblrKVtjY3w9nhYp9YDtHlZ5C3TlL3O3l/jAgpG3t9jCyO9qeV5CMbv3dYDOWS3JO8TuONVR2fxbzS8u9TA5RctXF3ecvh2pjZT22xNkZMwjaVpEXLdEYyxKKkJZx8RrJ5jKxOC4/5GUdJI1ObR2HWuUrL7/XRuVmHV/f4WRf45jKwPu6hpI1OIpmam75OQj01Nz3J2rh7KHEM3VyzsScltYCTT6OUH3fuJ2/XUaJMs3kml+RX5XWaXLeqI1lXr0t2beOhFGSa/kY/NTdtRLPaGBl/3A8raX+aE5EZ50u4o4xkfozIktVi4TE/Iyi5usTzKjXjXK3j2Pq5ZOK0hunQtsk6Z2Z1230v+6rajqN38OR0UmypeeRZbxwj65tFy1ydQ6k2j8JccnjqiqcY7Qgze/m6bM/s4XPnLt342DKzhgd882niGdWpNy4RM0tt2kD6qN5ASiyhJW35JY5GVBwlvQdA84l1Zm0RCEHnQ4qZNZzgpUc1GX3u0tPniqcvXnr06otPX6RNmgSd3rx58VKImNf/5tMKvYqZLQpNp1IPgcYUfuwLG/wVkmrr7o2LjxGwb1x6tHiMOGLFXT598dJzbxwaWlPFZcQI/0tP02AR0fwBKVd7S13si9CIMLPabY12zG3N+F/V7PYhUbcqjT1mdlwS/TqZ0isIxmP6dzQmcnOsOmcl8bOGspzSKd2jCVDNn5Zj6qdrFTNbFIp+VVep6mkud+wn1XZtRUkSU8t6SmVFb3ot6z6ompiiUN3OXBMRuzzjsKaAq13D/u5azS9rktEQqasrV/Z2r2+cv7D6tesbK4+snn9khVhUeiPB9nnNsZL83tceWd3SPYr0NBTq9dXikVV1rWJmi2Llwqq5ynGpmgzVe2aJ8109/0hBJoqVlaJQLLDqua5M6D2812sOOG0phjToZ9G9wrVlnNeMMCOjRRQtJ0xXni0fHn3l4Svl+fWnVkbfOr/+lYdGTz30JWJR6Y0Ezz6lOVYiZ69866HRNd1DlKilUM+PiodG6lrFzBbFV1ZG5irf0Pt6zyxxvqOnHirIRPGlrxSFYoFVz3llQu/hPV9zwDGz1uf3uUzGJc3zaoo5vPvyJ/a2zIK7Nriju37deEptvLIsgLm7qh92SaDuvOV4UroVS/jU6klOpyVt6NHbW3OStFlCrRI0lRmspTyd5E+1AAjv/cGqaKR237jVNl/N8NifsvuRdWeAEkebX1X7Rtp3jbsZxh5KUkRmO3IQuy9J30+PzLbRrM7aGIXrHrcinNpts42r7Ynd+2aZbvKN/1cNSzhGXIraleR0Qt+PNcdOO9/01mK7VzrUaTEMsiWCp5X0PSE8Q5T0w7/OH97OS+o9XzbrUn7OamOUlMzOI3WVyR9CMz2PuKRtmy9EsiiFY5RESWeI3l6k4AwlHTLBPA2fH7w8Z9mSGCM3QLwRzOJg5l5N/85BIOm+DGvkcP366T07cZ36CYpxo0nJq+p7sierb8uSkrqCPWWDysfuR8Szzp872XHnI9g47q7a8Kv0YHLzXmXgVYJEA0GeFUq0uYbMZl5e5XQ2zk1XwWpzM8x5F3utfiYldRo7rHKxh2OUUVodbAAAIABJREFUQmk+9TO0zistazdUWlclojXE1WH3tWuK/XEWa2OU8nM+9TNtPbzHhRnikHG5oRv1+5GTDPiyuiSvmbztZ51fGXJzM5R0o1D7ltSXzM1NTzI7Nz3J2rh7eHIM83OTS2bnpmeddiQm1zZcUi2R1a9NpdY2ttrwq6Y1PCmvrGTQztU6I1rVTw+lIH94XtVzydW6xrnp/KyNUTg7rGTz3LSSSkN1kI09N0Ycw3r9DFFydSnIljpKTjLA1p9xNgozLsE9zlsJ6Ocat8bw1yEhnm4+ZueRZ71xjKzO+hglUarNo5ykfY6LMbMv3A22zcb2zN64+lhRKL61sDtAzz1GNKJ6vwFxeZoZVJSr2lerN5AGe2bNJYqHfezpcy/e8JhZe3YRSMCoD1FmlrapKsrvqnprwRvEz1pmljbMPv2GYq4V9fyuYjyfsxtX3S5j3f9uhZ5+X8SLjxYhG14pDISJEy8evUg8rH7jraFcVSB2MywRr0+/cZjAXzGzVy8Rma5Gttp5GkVj/p11ZtahTXu0ye2nr+roLK2smFmKV+1ffo6I8ks37vl7ZomRVBv1Nd1JDKZiZifq35HaCatPTRSFSv+onbOO0DSkp2Vmicm1fK6qnhFmlnbOqs2zpaJBJ3ovrerRFjUzqzVzHzRP2sjM6oj45cGeWU09OypZB1V/S4M25ChOQ5huny9WtxxXq5nZK6u0p/URtRNWndq6slIUxcoj9M/XrqjXIOjLDdG5ev66YmaJybV8bmhIvc2Ads5qHpbeQkB7Zm1Poc1pZlarZQ5UO3ADBjZ1yKPj2pzbZmcuOWCcdwG6TcQp5bw/JEyffaoYXTMvELDM7MMj4l4fUjth1alrD3+pKIqvPFQUxZe+9bB6DYLbpqqY3KfOK2aWmFzL54aG1NsMaOes5mHphbO0Z9b2FNqcZmY108ocMDtwtdGvKZ+5jHPG7LcltcYl5/ZX1TZe7+7r7ru6IWcWnmTbqRqf2J1af5VgV4TlWLNjo5Fec9ZXh0xSv/iAVhTuzQN8lcAl7TLK9AVrKS5JGuyx3gvg3dH5qoi39TNeipnV/Sx2D/n+mVmC1W4ZDmKneC06Bj17mJZUv8Drj5GHUrAi1IcaLlLqf9xq2+0TsZJ8NEM//TFKSVop8zMdkVWQjt1h2KjTSQY+R/gC95IHvZh2W4brKHFJDq8/j3TyqrGOjJEN0vz0/FRpEJ1HTKfLlCSenk6LVHRPjZO0UpXOMEPSsYeSDpna3Axi94bGDnpkvge5yg/ztc5N9ka+9aj106shvHo/qb4AW1HfBjVa18VHX56JyPG8jZJ8C3DtuyU+1rwdQT4YQTeyUTbN1ZDgqtrscBnsJUATB+FyNZrJnk5WTtPVpnlu1nW6uRnmvIu9Vj+Tkm67kM7nNEr1MQrnEZs7HNJ67A7DRp1OkiuMIs8lebuh0uZzyVWbsfradaS+L1RZF8TOLWpX3RilJC1aBoMMSqTBIpWP3UrJdPr5GWaIQ6Y2j5KS7hKbSxFJXjZd28+6IAqe/wFKgSQfhbykHqPsd/OkjL6b9tc2fDQD61qnG3cvdo5hfm5yyezc5NZ5u54hwdlM7PxUcFWAJ5cM2nnJYIw8lIL84Yek1P+4Wtc0N3n+aFfdGNEh/8/OSfvTYJCPKD83nfV2eObnJq9LGhadNnWUnCQHs6mChWPEn2X0V636V3BqzzIcS7ZWbL7HcYukJPEcx3SGuDbUebdxOLpmcCix2RdjZn/0uYSZ1RswiYw7fE6/qXP+xNzgFlPM7OCOnRIHODN7zJBV+bM7YWtbRFO859i+9GAyohfFpsR4/9EMcQ31dh86ZzPaONzIzHJ6sam9dcG89IC41OuJV7sGShwzG/Qf7bBbbWkfdq+sVq93SItV22kdYWpfU+DeV5BpXFsxLz0gLvW87K94HclQ0ofjaSsfHtFLG+iuxu++7v2A+ldc9eO9/Y2VpKT++jS164rr1Put2BtpvTu6er+VexMWW6LQTTUlSWspWkgb2jEjSbd0tebWXxDnJJWoJX31coatDvk7nur7IFJ46nczOfYkQP6q4lDcaxz9N9J6sdMLrkajkXprKm/XmQV2lr5nZq/jDWP3JM2DiaZxM5LaK7uWraE0VU+z+sVqE/Y21foKiUvqtn6Hr1bJg2d+8q/3688kMyZJy8PMHk8uWU4olxI7iz0M/VwNUPIkmX7tp/ekobeH6Hh5u44SP1vD0wPJH+vMPOJ+5ucRl8zPI0+yNo9SftbHKImSfoeaW0kT9OzDkeHztJZLthioNzbnx4jrD9rBLOa1js/oOjfKJY9RP5M1WVchx6Vm/KzV5KROHZGkzvMNszVmVr8jUtf5hnHnI5gfd15D+FW1ceeVwWsvQP3ks4P7Vp+bXs7z2Gv1MynJN1VlUaqPUdLPudRPbp1XG95urrS6nNqdsB5KvNLq+e44NX8dwi3Wxyjl53zqZ8r6tDZGYewOmdo8SkryDKzfuYKayQ99PHll4Pkfub+z+y8fhSbJ7NqG6dTo8bUNx5P7WR93DyWOYX5ucsn83GR+NsxNLlkbdy8ifgdkV0Xw5JK83bJ+eijx/OF38Houccns3OT5Ux+jZOx2WRB/RvDiNb9CpFUFK8DA+pHXnx5KvC4F2VJfBekvk0r1chtNYdvfV+Ox87nD26Z+8mcZvkqprRlSOnV/ah5xi/kx4pL1+plEqTaPkpLsOS7CzAa0bPo9swu3g/KY3NwRLgczewTQOrxkcGa2TpI29qjqKeJwG1U5gT50OuXRxrwozta7XPM06NzczrtRP3s8ijPJnNZ53m4NdaItZGb5nThoB8/2wVl+2EaS39Ez7XDdkxbtSdK7o/NHi6DdJnaPAeEABu3g6WXusacNemci310H4LhDGiTZZ3li97BIHwClNDbVmcFRkuenfBafZslqaLOtwcc96111sqe7TGUg2wJKWXjMSaA0IEry+ilxMsIPpi/D3ExjU50BShUW6dYpR0m+YklD6J3pCU95tZFIgpk9Fr8MZrZDmvUIqsDMatpU1ZqO2d4oIes650ZxdmuoW211gvXIPZ1QnHUett7TraFOtNHTS8ADpg77kfTu2+mDnu7oaYPemXbPeCkAg/42eHrepA+WCSUws40I0HDKPuCvJUC1QUmO/LD1c1msp4uWd6ZdpZUMen03qGfQOxi8fnrepA+AUhqb6gxQqrBIt3pCSV4/0655ZzA3PTgSB0ApAYzXDZQ8OBIHVBmCZ5bUYZuVVcJa2N1qjOTVRiIZYWZvlof1DwGE/4DAgiGwubm5YB7BHSAABIAAEAACQAAIHA8BMet3PDO4GggAASBw4hBA/TxxQ4qAgMBpQCDCzOJtBvLNm9gzK8eqD0nsmcWe2VbbVLFntpNdrm4rbifa6Eab+iI06O9HMvyqNHHc6hvUhI6wu5VOyXetJAOUJI9kBL3sM/S38WHSJI77yiWg1IhAP7kkz89h6+eyWE/Mm7Cb6mfjiGuBNpKhmcRxq1mc0BF296QTKIVA146RSzVIIh09oSTPz4hPsa6e5lHMVKSvlXV57HLJiE+xrlZ+xhRE+nrSKY9dLhnxPtbVU0QxU5G+VtblscslIz7Fulo9y8QURPpaxR65PtbVeQUDM4u3GRwLgT74VrlOMLNgZsHMOp5U0uiES3WGOtHW6u7bBwsQu9VG+nq6o0csxbra3fsDRjt12IbDjTkV6VsmlMT8SyTOWNfgscecivS1yyWg1IgADbzs04bll+vsoyqePJ2RmRDrwuyIoRL2AaUQkdgxUIqhEvb1hJK8foYOJY5xf08A43UDJQ+OxAFQSgDjdVNlSD28BP1tVlaejfRBqzGSVxuJJJjZY/GS2DMrZ1H7kAQzC2YWzKzjSSWNTrhUZ6gTbc1336tFcVXdodvcp5fljp5eGHhnmp9epupPoGLPbJ4j4yjlJd3Zodd8Xh6kD7pcRwIl9VeeG9bQPaPUYJ3lp7zWNUj2XGkbrLtnraHrfAPyPY97eop7Z1rNd+/K9EErnUApDaQ50+6u7WZ0voH7UR4ffZZSWfYBnhKggBJQiiLQ891QvmZorMZaoNU9Tq6zodq0RCnCzK69cDd4ocHN8rAPWu0E6AQzO+wggpkFMwtm1vGkkkYnXKoz1Im2CDO7UhRPFcWTipB9sigu2y9O60/sl63kU1ZGP95zyctFsaK0rTBVjAUI777leDQpJ+PReDLlp2p39HIyGo0nk3EgpzgdfuFsNptOtJD9aU+HOsvxaDSm/0ajcWmF1M/IM96oKCZFMVaE7LgoSvscwmPXYQKlKErBQrO0eE4sklqAP5OkByj+t5tPQC4BJYdAZsY5Gd3oIpca1vrOYjDfM+UukHxVFcY5VtrwKUtSl3QFc3cEV7d1ox7RU/ZrvCfDO4JXT9MTuV2ldaPQ3bh7fs5mM9QQ/1aISltlSDqNgZK8fgLPCqsu7lwVnrqFCoYKxm+UbVbU8jWDn3UL/HTGoZipBzf9HMeeOyLM7MFPPgczKyQcwcwKgepJDMwsmFkws44nlTQ64VKdoU60hczsU4w/fUoRr+5hu/4cftkK6+fwJxUD+yqprO7oTkY33KEmc/kqwa4jFStajol2Han/JmWNb51OGHlaTsaTik4N+VaPmVW0KymN6JyVY0PIUmMaWK9WzzPFIToqdqIOJ+k9sy5koMRRqq+QNKRjxcyOFesd/F11b4Bms3JCo2h/1MfdDugy5xJQ0ghM2Jcf9RnXA0refA/080Ne615V9VB/laVn/ZOKfl1R9TCQnHulrWqy+8ZIu6rr9opyNajer6pbgPtyTpO57ju2ICItrH/BoqbTe3LzJvIxKi0fCP2UhRoyl9nhjabir5f+ro1c0gh0VGnl9bPKJa8suBu7uc3j/m6AAkqlXQxgrdjzilq+ZqhmMT1wLfDTmaDOR5jZv/oEzKz0FQdgZnuiXIVqwcyCmQUz63hSSaMTLtUZ6kSbx6K+arfK6kd3x8lqSrH+HH5ZyT/pE7jBs73jJXVD/3u14nD5HZ3aJW2XtXtmq12uwbqc9gG4PbVmqWqEA0mlk/bXKlJ2MnU7aGtsryXyyAf1nOlZ95409CZQ9yQztWRi9G0GQElz2QFK9RWSZmM1s6CFG5hZItCnUzNasXFf/lwCShqB/IzrASVvvgf6+WFQFYNypytqdIep/qWEOVbayFOW5k/1l2Rul2sQEffTRZe5I7jfkPBj9+p8QC74NdlDfu7j7vl5Mu5HPF01f41K6xgNTe7QzcP/lOqrwbH/tSvuR2KUQjyDC90h/24+KAt0iPu7Skug5BIGFUxDMZcKJl8z8PvmQj+d8URK5FKEmQ02zH74yed4m0GKKAQzm0JmPv1gZsHMgpl1PKmk0QmX6gx1oi1kZoOdXG4DVMC3Rndd6c5A0j3M64bedaXJSiXJ7+jUtqtz9dPjRrmk/62sR6RGGDpzpdaW1OlM24Yn6T1pBPtKAs7R4QCU+M7iAKX6Csntd9NPy1og+0wympRlab6gj4z7CcgloKQRyM+4HlDy5nugnx8GPGZQ7nx20nvOmXul9azz7b1uL7+uV0FE3E8XXYqZdaWvppNXb1tgXbU/aqXlAxHsmUUNyXCOqLQSXgMoHQMlef2sKoO9X5v6oH4NH/d3QhKrIF7q+Z5Z1Pk+67x8zVDN4nDP7II9nfFESqwZwMxKt8dGqUYws1FY5tYJZhbMLJhZx5NKGp1wqc5QJ9pCZla//VDvpdI7W92TefDErp/t9Q4p/TpadxWXdA/zjpl1v0KbYGbN/lbatuo9sfN7v9pbq18KOynN697Mq2m9Vax3jdaW1hk8GPjWwyeNkd1TM1UNxxzx2B0zC5TqKNVXSA5St19p2vBMYn+Fll5qEBl3+x5A9btV6XGnfdqLmktAySHg0mMuuRTOd+dG0Ajme1DuMszs3Ctt5CnL1SWhn+4tuvZdNKHOzpnZWVHMd9y9O4beM6t/32J570dBxpYMUlRaTb/SzcP/ACX3dni+thGjFOIZXOgOs5wj7u/mLxkAJZcwmk1zNwVUsD4rWHh/dwuA/DevS76iBjMLZvZYCMyNhI0aAjMLZhbMrONJJY1OuFRnqBNtEWbWPV0HjYCDCM7ywzaS4ZNw4jjCuzlJx6iqnpyku6S9pPxJI1zNcGR4+5SjxJfamTZ/JvGHLzjqZtwXLZcyyPBTQImjkWq3QWnY+d5HDelAp+OddR3rp4K1QD410EF/m3EPqkrqMFdtUEMsakDJIpH7eSJRks/iHDTsXA4lJhb/jtYJYG5aKHJ4AiWgpPY6yNcMFrDazyXMJTCzx+IlsWc2SpjOrRPMLJhZMLOOJ5U0OuFSnaFOtJ0EZnY6da+cbViX+8uG3Nq0Jil/0pCvZuSSvjvJo1xEi4ZSwJ6kDufMqgAlm1ynPJeGne/yyjBXSf1yG/f1EphZO1m8n6ghFo5TXkMsDA0/TyRK8vrZgI49nUPJyuifOUnMTYsVULJI5H6ecpTkq4skiEs44yLM7M3ysP6hh2f8BwQWDIHNzc0F8wjuAAEgAASAABAAAkDgeAikvioI+o9nBFcDASAABE4gAkGdTB2ewMgREhAAAkuMQISZjf4FsCQbfbpP5L7NON3IzCf6zc3NrgzNbSj7MNSHzjywc7PYraFuteUhanV2bo51a6gTbXT/dHug8o1+JIUjJQ+2J0n5HpA+8DyBKKUe1YL+Oe+Z9YEePpcCNFKHQCmFDO9vg9Kw872PGjKsTn9iJY/ofsSHLNNuI5m055/oab77RpJHrawDpSSO9gRyySKR+9kTSvL8zDnHzrWaHey6XLMnnfLY5ZK5MNi5niJiFnLNVtblscslc86xc638ZNflmj3plMcul8yFwc61ejZk1+WaS4ESmNncEDaek49xoyoIHAEBMLMatPnn4dwsdmuoW21HyNjUJXNzrFtDnWhrdfft49k+NShBvzzYniTl6x6g1IwVDZLs04ZNC3ImddhThqTMBf09PQkHVlKHg8eecizoHxwleX72Md9Pns5gfFOHg497yrGgf/B51CI/UWkbEcD9qBEi+hObslt2S8lgZqUOB59xKceCfqAUABI9BEpRWILOwVGSr0MCz1OHPc3ibu+Gx2Bm7bsb7M8UDie5PznG07Lk7x3sA4O+TfStvwtMwMxqFJN52AXIUR1zs9itoW61RZE5WufcHOvWUCfa6N6f3yrrzvYjKRwyebA9Sba49zvE8o02eJ5AlCSPguoZb1lil/vZIpeAUiMCNOFlnzYsv1znsPVzWaxjdjQi0OrO1SI/e5gdjbFogVYR9aETKDWi2hP7I0e+0cMFySW5n/LY5ZJy68siKY9dLrksscv9lMcul2xhPf8I4862WVnJrcsl5bFLJCPM7OUf/Sx4ocHN8jDiXzmZTGez6WQ0op+Z/6Yx7pZ1xk5rdUyI6zfd9MP93ZWqxSWpzcXYBepEKNv2OHXXLyfj8biMaPMciJzPdAWXpkw4MdOgHwaleoObq+RUr6ffXanh5JexHibFJDy91hUzLlrMk3BXxrW506qRZmanpQ26pP90hk5Z21ek/ghg2JU+nlbqlc78BPD1BDlTqZq1VuUUBzpdPzWmXG0OAe+qpoOcxdq1LEYTpBywuiGurWaqoaOureEChV9VZVQuyZ1vVO4EjuCYu7ZVo1tDTJua2vRPqwb5DmZWMoLtnl7ceiXfADMroQyGXvNJ0qPt352TrA5Jhma47AOUJEC1QUmO/LJwo8P6KZ9HLZCXDDq+3QFKjQig0jZC1PJ+JJ/F8sqwLJLy2OWSyxK73E957HJJufVlkZTHLpeUxy5fM8h19iEpj10iGWNmr8uZ2elkUpaTSTkZEzurudpyPJlS/4wasymdmpIAk2Gdo3E5VYcGK9UmlVpGnzICSr/uJ95tWo7HRLlNJ5USulLZVC7pIydGnliF1SXCQYqKMWKCn9cQEDVb99w6QOCogOgf1VlFPRkVYx2GQ1WxlxpCZSluQtPQk7EeEUUfWpTqp5TRqbZVjscTNUqWdar007iO1SibcNxoVg6r4SAXrWmbDDPKBOWCN0zatPpXS0xL47O9MIyXw1u1U8ws0coTYsZVIppRmE7YiFQ6TCsxlDU5UlpOJpZ4VzQUZVhMMNrnGWKqtBLtpLvQ0tMKDkcQavLLCeVpZXUVV65hd1cLTTh53fCiCM4FhyxGXROC8/nD0BDX5q60MbgOne02mavuUFt1JtHi5lRBC+XEpsML/ePWjvmXy4+6NVRpm04mVEFU7Zc3lN9gZiXD14ojk69m5JISJ9vyg33olKx7SIZyV/Zpw6b1EVEfOuWxyyX78HNYnfLY5ZLyiOQ65bP4NEv2gjxqSCMCqLSNEOF+JIGoJUry+imvDMsiKY9dLrksscv9lMcul5RbXxZJeexySXns8hWLXGcfkvLYJZIRZvb7n3wu3DOr2S/i5yaj0Xg8Hil+loi88Yg6NFs7nqidilyGaFPTqYQ0kavYNCNWGppXU2u0MdfqV2ymBtYQYoZp0iSc8kbxA+oSIsyMmLlQiXmXCEcpJlYRE/xsSUhMFBwRz5kDyiXNZhhvp7TZli5WzGwVNfVTr92enDDhxIgmMS5VKGkN7hS3ReQljZq9iumnITBcOw2tHTjjsBsOZ5oPtOFZlQsc83AsNJPKRtlps1FwfKt2nJklhHU2KC55NNIsrTFq8KiU6FZ8KEMpe+wpCahOK5P4GRqyqoj/tt8cmEsVH2vI7tIQ5/x7CGch1OlOUEPtflYDG0FAbMJTmeeCA9FqCs4orei/Fq/6iIRmEdN2FPruGxf1BQN9O0NC9eSJaKt7G/RYc3XnW5kOtAaHR3EsUCE77NZQpc1MOl0pXMloaiifwcxKhq4VkyhfzcglJU6CmQVKjQhURaNJdHBJyRqaZMhR2acNyy/XKZ/Fp1myKd3M+VajKR8jufVlkZTHLpdcltjlfspjl0vKrS+LpDz2PiSXBSW5n0CpESvU+UaIzG80itc28qyTmDbW87/25862WVnJrcsl5bFLJCPM7OUX7sqYWbNRUHGhhoXV+0Bpu6fZujolXpT21ZZqE6vdEVl1Em3mNiCqTY5qyy0RLHQh0VK1nafUT6yLoUwU++mUmNcraNJEbTKtmBWmMLQrHIBALPrkYLfWkQv1qF1E6qSRcN4Si1aayFSn5Ta1LsvMpkwovBTDrf9hKNVPEftpbdEg2g2+iknTFK0iSBUfbJjOauDMMBlOVfOG5sAlA42hGn2ifL1hCga3pGO+q9p5WyfX+BDEmNkpceLEMhMzp+hOE1iEl2S6okPJzvtNm1OMdfQF0kehIaaKaFK2L9rR0zqL9CkjYJlnbSfUWbOuNdQRkJsIVDZa9ORtjOanPfRkEgcRQ/7lJihTcsLvYwKtEW2BRP3Qmqs738p0XTHvOYpj/Hpxu1tDVtu0pAln/i9uqCqOtxnIxq7dOtKtV/INvM1Asugces0nSxAiCOWSktUhyZBS2aeNdbmfw0rKY5dLyiOS6zzNfKs89l6Qx+xoRAA1pBEiVFoJRC1RktdPeWVYFkl57HLJZYld7qc8drmk3PqySMpjl0vKY+/j/i63LpeUxy6RjDGzwrcZCF3OinEeKiuYO+krCX4dPH6hf0lcRtIrfxaSaDtxMoa5Uvs2LUndaZAxZlYbMMylYp8V3a1erDGeEAUcZXtbDCW9nWM0UrQS0c3EA6tXJ8hC8wxxVebri+q9CI6e9pnZyJcKnk7fDadEvfeDPOUIuLONJnytLVgAetGthUt/T6O/nAgUpg7D0Lg2fU3A8hty2/Kpvt5Qm382csTNMUNGkvWokqLrStx0RDnrau0Yu7ZVs1tDTpuabzTfWzW058T+5AlEd7YfSSGALthG+Z4kJXd0kgFKksc8GiTZB5yjBCig1DVK8vwctn4ui/XGul3djyRD2ZInkltfFskW+SnGc1lil/sJlBqxavX9H/AcCs9Gu1qgp9VvH9aRS42o9jQ3G+26XJKvLuQ6+5DsNpcizGywYfbDTz6P/wUwYXAnWkxeg040DIMFl2ZmW7s0t6E8pqHolwrH1BmAFTURyHRrMVDOD7s11K027ucx23NzrFtDnWjriUlclju6MHParZAcl51vtOFw5X4OK9ntCom0gXOUECtAqWuUWmRyfpq7s23mu7x+LoukvC61QF4y6KghQKkRAbrNyD6otBKggCdQylb8ditqCZio8z2gJF9dZEe7OtnTel5evSWSYGarATtCSz7GR1COSxoROIXMbBST+efh3Cx2a6hbbdGxOFrn3Bzr1lAn2sDMSnKm3TrScTH5RhumRuIk3jMLlBoRkBeNwSUla2iSIUdlnzasilyn/OnlNEs2ZqYWaDWa8jGSW18WSXnscslliV3upzx2uaTc+rJIymPvQ3JZUJL7CZQasUKdb4QI75mVQNQHShFm9mZ5WP+otSf+AQKLhcDm5uZiOQRvgAAQAAJAAAgAASBwTATEbO8x7eByIAAEgMBJQwD186SNKOIBAqcCgQgzi7cZCGnyVvuD5DohKUcAe2Y1VvK9RXJs85Jzs9itoW615SFqdXZujnVrqBNtdKfNb+10Z/uRFI6UPNieJFvsg3CI5Rtt8JzNCslHxQ7JBgQGR6lFLomfb5dlHsn9HBalFtbz09ydbTPfh63JfVhflnGX+zmsZIv8RA1pRIBuCbJPm333w2aI3Lo89j4k5X4uiyRQahwpeu4Qzzi5ZKNdLaBWgCLZwSXlscslRZG3/OvQcp19SMpjl0iCmRWOUVxMPmfi16P3eAiAmdX4zT8P52axW0Pdajte8npXz82xbg11og3MrJcKiYN260jHxeQbbZgaCS2rl1KQbERATZwG9lYr6UlSsjokGTIv+4AvkADVBiU58n3wmCdPZ6Kyht2tcl4+RqGZxLH8ljq4pDx2uWQClbB78NhDhxLHyKUEMF53Tygh65oRwP184bt1AAAgAElEQVRddtduRlLraXN/9+ZA+mDwWiePXS6ZDtc7Q5Uh/wjjzg6NvDx2ieQxmNnpVP+Ne/vTA/SUHMTnzHRaqv80Ph1DMS3LiN6p/i9ny4yT9s2MXU5+Gc6BmdWjFM/DPkdwbha7NdSttg4Bnptj3RrqRFuru6/8Pi2XFI6jPNieJCV3dJJps5ppg9KQTGIj19krj3nyrLfIJcmjC/72RQ8otRgj93ySb/RTGeQ1ZFhJeZ1vgXwP4y73c1hJoNSIP92LxRkil2y0qwV6Wof0YV0eex+SfUQ0rE6g1Ig/5mYjRH28QZUysw2LKl8zSMJp9Zvu7fzstM5HmNmDH30evNDgZnkYibmcTKaz2XQyGtHPzH9EGtZOs87YaS3PhLgC000/nOaqxSWpzcXYBepEKNv2OD5yGhmri9msnLSd9qcVrv8MJMrJeDwujRg7R4RrDWV2fjYjr6aTsRqs6WRklFQuOdP2KvpZU6ngdKJDN9LM7LQ0vism2oTB26Hr8aEMpczx1KmnNLKmEsJBNzfEr+Xt4BLvcFpOymk5mdgkoJNcpy/shXwcE57ajMVATh06u/Y7i3qqxi5TfTw0p2c2U3G1UGP0c21Jk+6EdtfOAQ2lPXJC3TTaOXYMm90aYtpUsaB/WjUokp6YxGW5owsHs906Mk/QuLNtmJqTx06e5ojw5NY479rNOPG6vNGuFmhn3c3ofKPNfJfXz2WR7AX5HsZd7uewkqghjfi3m8XIpUYEaMUp+7SRbBxHLcCWuw1XDC4JlBpGyPx6F3KpAafBK5h8ddEQiT3d09zsdsZFmNnLL9wVM7PTyaQkkkgTfpqRLMfEAE7KGTVmiguckgCTYZ2jcen4QkJOnSKVWkb9qzs1t2gVEgNQjsfEzSia0ShRjBVdpFzSR06MHLMKQ7t21Nr9jI9xOR6Nx+OJ9o2MqvArizo05aFxSPdMRsW49ILVtLKhU8k1Da5mVcvJWIFvQAtBDq8lr0aOkFUQBS45/LWqSTmdlgZJA36osx1a3UunmFnirxV1SWOv8CkJu6pddyU+lHU5ytFyMrH0OG9HhWudlSF+LW/bSwIS0BLlijH3OfNKp73W/FQsmQ7cc9uKyU3YK8zPpMVALoBLnTX+1CVjPZUhBtF0YoYy+aWQBct+NWNUV9pitsI+jp6qZqEAP05Y5CKZdjvHMoqaTnVrqNI2nUwmNEJU++UN5S3d+/OEgjvbj2QTZuZ8FWzTBT1Jtrj3O8TyjTZ4nmYe8+TF3iKXxE/CTdNiUeaR3M9hUWphPT/N3dk2833YmtyH9WUZd7mfw0q2yE/UkEYEaNEg+7TZcTZshsity2PvQ1Lu57JIAqXGkRqcc2z0UAv09DQhtz5sLslXAvKI+pDsFqUIM7smZmY1+6WY2RFxkSO9IZNosRF1EG1C/KP+3f5JJcM6lZAmchWbVmqxUm3xVEzthMhKfq1jYyzjpJlLpYQuK4kaMJfQxkIjZnayKjHNz870JcJRionF54y2pGykItWYKM6WOL4p7YQl8lq1q2Cpn3ptyMSuTiYaaMWA2KAjINeuJcLEEYqTsea+ibZUCNNgTsbqf2a8VAf9k/Ynhsk8++LMLEVkhpbYa0vH83bdyfhQ1uV0jwOyyq+UaNjvGcroKSdqPpkfjhOnQaLsJhLf/efpdL2mYZKdjrg5OmxhItCatRjIBnYDJ2rCfodnyF5q5rI9VHXClBv3bZAOu6TJozBTaj1tvqHEkUFPf9uivwrSkvYE/eqAatsvh3yLCbVhd3vHQg3C424NVdrMpNPfyrna1NRQToOZlYxdu3Wk42LyjTZMzcljJ09zRN2uI0kb+AIJsdIGpRZjlJ/m7myb+S5/IloWSUmZXYTf35T7Oaxki/yUTA3UEKDUiADdZmSfNpLDzqM+rAOlRlTbrajFWddoVwss0Xpp2FySry6GRb5blCLM7OXrP5PtmTUsn+JCK1pE71M1bN9kSmQQ7astDTuiOZWqc6Soxopl0hwHsU9Khnhdsye02jNLbCFtSDXEjCJh3S5G83qFSo8V055YhaFd4aAGYvHZRaGqXZvaRxM+s+jCJ1yIyCEW1e7q5IwP16SINU3RKtJV8bWWgIyAHFyrqW51pdlRynHT/UoLU6Wc45udQ50BHHM/jDGzU2Ku6bsBtaFav83C7jqmfY22HTgbH8pAyB0yTtDllzuZb3iG0npoZOk7BvWf4v40R0+DZ0l8Z8jT6XpVg1sIXG1lwteafn9CIKcPmRMp/KPXhS9qsHpizGz1/YE5q+cGZfbYvXElA1TUAWvQIueOqSiJLEbV1jvbOlbXIOzp1pDVNi1pwpn/ixuqiuNtBrKRa7eOdFxMvtGGqTnNPObJi73bdSRpa8M5ylK+xV2mJ+vDotTCen6au7Nt5rv8iWhZJOVZ1wJ5PLE3IkCTU/ZBDZEABZRkKCHrmhHA3EQuZe+L7Z47JGC2XCvKVxfZOKqTS7FWjDCz3/9E9p7ZKtKjt9rSNFFLvhL9i85RwarTv6Tqb9uSj3FXFtt6mJFfQJcy3kZPxZhZLWgoa3opq6KT9W/Vu3Zdm3wo6c2y9HZl9ZZT3q4rjfVUhvi1vK2uUhxgOR7pTYh677naVc5IfKe+0um6VIPYQ/1mDfVb/ZXb7U34ils8M3twWYYz0JY5rEJjELkvEtzbGEwysy9+9Hcw5osiu+u80pYxaU956LEvivR5oUWrrOFnK8cadGVPd2vIaVPzjdBv1dCe0r3fcQf5Rj+SWcCqky7YqivR6kmyeZ2tF0Z9oYS/ANaAgBr3BhlN8g4u2SKXelhtJ+ZN2N3TPArNJI6HfyYRIz9s/VwW64lxDrsHH/fQocTxKZ8dCVTCbqAUIhI7PpEoye9xMUgifYOjFPEp1oUKFkMl7ANKISKx48FRkq8uYu5H+nqaxfJqI5GMMLPBhtkPP/k8/hfAIiGfui75GJ86aOYScJqZbW1+bkPZh6E+dOYRnJvFbg11qy0PUauzc3OsW0OdaKN7f56QdWf7kRSOlDzYniQld3SS6Qul5eAcT97+1j4iapFLYn5wWeaR3M9hUWph3VXIfKOfyjBs9ZZbX5Zxl/s5rGSL/EQNaUSAFg2yD/bMSoACnkApWx8H5xyz3lUne3qaqAxkW4Oj1Mf9PRtxdbIV8vLqLZEEM1sNwxFa8pE7gnJc0ogAmFkN0fzzcG4WuzXUrbbG/JQLzM2xbg11oq0nJnFZ7ujCJGm3QsoTNO5sG6amD34QOhsRUFOse05csjokGTIv+4AvkADVBiU58vJad5ole6m0kkFv+fubcj+HlWyRn0CpEQFU2kaIWt6P5Pk57Dzqw7o8drlkH34Oq1Meu1xy2Ij6sC6PXS4p91O+YpHr7ENSHrtEMsLM3iwP6x+1Qsc/QGCxENjc3Fwsh+ANEAACQAAIAAEgAASOiYCEqtBsxTEN4XIgAASAwAlDAPXzhA0owgECpwOBCDOLtxkICfXwzxPJL4NkRwhgz6wGspOti63GZG4WuzXUrbZWiOWF5+ZYt4Y60Ua3WreLM9/oRzI/NO6sPNieJCXftZIMUJI8ktEgyT5t9jm6bMk3esqQvFF3ljJEHLtc0unPNwaPPe+eOzs4SnLkh62fy2LdjWy+Mfi4591zZwefRy3yU1xtXHT5xuCx591zZ5FLDopMoyeU5PmZ8Y2fQtZxNFJtoJRChvcDJY5Gqk2VIf9I6M4OvUqXVxuJJJjZVEqI+uWzS6QOQi0RADOrAZt/Hs7NYreGutXWMltz4nNzrFtDnWhrdfeV36flkrmBYefkwfYkKbmjk0yb1cypRgl8QSMClMqyz9ArYzZTc81Wc1Meu1wy5xw7R7NYjLx8Fp9mSYZurtkOefEY5Uyyc63yk12Xa/aks0V+AqVGBNrM99xgs3M9jTuzkGu2st5HLsl15sJg51pFxK7LNXvSKY9dLpkLg53rKSJmIddsZV0eu1wy5xw718pPdl2u2ZNOeexyyVwY7FyrZxl2Xa65FCjFmdm/+uRzvnM2/hfAplP9h9HtzxwWJ/VcfIyn01L95/5wfLfhG/VttR/xsm5971gbmFkNaDwPOwbbUzc3i90a6labh8jxDubmWLeGOtHW6u7bB7MgHDp5sD1Jytc9QKkZKxok2QecowQooNQ1SvL87GO+nzyd8jrfAnnJoKtvy+TWl0USKDWOFFj+Roj07572kUtynRInW/2ObE8rQLmf8tjlknLryyIpj10uuSyxy/2Uxy6XbGHd7YrNN4Zef8pjl0hGmNm1F177/gt7l39UkbNxZracTKaz2XQyGtHPzH/TGHfLOmOntTomxPWbbvph2OHZrGpxSWpzMXZB7pJQRfI4Xn81MvYiZtM6mXKJidqrjf/VYTkel4Q7/dS9katMl3dGeTWdqFEzsBitlRi1IoMZ6aocYldUV8cVVeery4/VijOzmoPWTjOS3BLmBF/9v/hQ1uUUdES8Gy3aQFRl9GJapJsT3M+Z0tNCjae80ul1qwNuhaFRF2zVk7PYSlGTcLeGrDaVtPTPgjRYVjQBcszzFoFjqjGXM21HQ5L0gJmVDEa7Z7z8IsadbbO7VuLkIjy9SNY9JEO5K/u4it0EAZsODaKDS8pjl0s2xGxPDx67daThZ6sM6QMluc6Tx6L2EVHDeNvTg4+7daTh5+DzqEV+otI2IkDDKfvgfiQBCngCpWwFRZ3PwmNODo6SfCUgCae/JxR59ZZIRpjZ79OG2buXX7jrts2mmdnpZFKWk0k5GRM7qxnJcjyZUv+MGrMpnZqSAJNhnaNxOVWHBlXVJpVaRp8yAoZbVAqJVLEk5aRSQlcqm8olfeTE6EKrsLpEOJxRsfjaqByPxuPxRBGoVfjMYuV55RLBN1ZgEt2t8CSThCRjYWcVIWtakavo8lKRThxa7dVI87nVVZq5VgYrW8qB6WRUkHQ5GZE75gc/NWXI6371r3Z6Wo79xFBsbRVZFNCWnSlmdjYzQKlE9JRWAHrdbagxxUFpPVq/jtrXlzyqcobpsdos266uDnhaxmurK5mFSifrNE1mpY4Go+jV8FS8fGgiUJyzGIge77BbQ0ab+oKCysmCNBQ7eTycpFf3gqcuVJNpa0iV13Tvd1xhvtGPpBA7OXQ9SUru6CQDlPBMks3pwVfbWe+qkz3No8pAtjU4SsPO92Frch/Ws6NdnRx83CtXsq1TPjuy2FQngVKFRbp1IlGS1880MN6ZwVHyvEkfoIKlsanOAKUKi3RrcJTkK4F0EN6ZnmaxvNpIJFPM7M8OXnjNvdMgxcwS+6j42HIyIi5SEXiKYRyPqEOzteOJ/t1+JkO0qelUQooxKiekz6gqDc2rSD61Mdfq1/SvQtqQbIYX07ST4okV5aJcom2lRsxcqMS8S7xRa3cQH2NtSdmIRhp1iSI1lDYxs5rVNDCYCMi3qqmI7+hVmgRXSkiRIfiYV7WrtJiSUAbo2jGR6WPiuRX7PlH/KaqdneLDpww5ePVwskEP/WmHdFw6zswSx23i1t8J2H3CHn6BxvhQBkLVoSVjp5PxaKTmQXUu3/INGT3ElNuvDczlPiHuCHTq9r/MEHwLZPNdfUPC0DA7smk6Kjaf/qUhjpgIgvKjCE52editIaONstTNtwVonAxm9giQqkyhe3+ekHVn+5EU5qs8FXuSlNzRSQYogZnN5vTgq+2sd9XJnuZRZSDbGhylYef7sDW5D+vZ0a5ODj7ulSvZ1imfHVlsqpNAqcIi3TqRKMnrZxoY78zgKHnepA9QwdLYVGeAUoVFujU4SvKVQDoI70xPs1hebSSSKWZWsmfW/Dq94kIVQ6eZPb1r1WxdnRKVSMxeqUkft6/WdhKtpQhAg53ikNQ/6kLii9weUqXfsJa0IdWwlPRChUqJeb1CpceKaU+sQn6JN2ytDuJjrFguw4lW4XOLll+tYqR9sYoUM/GOJyWRo2rvLbHVll+1rK2JI3bVRDOz3AsKqjr2bNnusWIzFTNOBLEaXOWm+WdkaGN+ykO+ikVvWqZjvlHaGnKRtEI6LpxgZm24dtOpISZdIsWUxYcyJsn5XcWo8j3OiQtYNzdk84BO055VtqM4QojTRLHbkBUD7rRyna7TNbgVtbtRzVZ12tHlNDpmh7sNxzfhtOlG3mIgfJzDbg0pbdOS2HTz/wVo0Ab3bsPMAN6tIavtaJCqXyvA2wwyo8VOtVshOS4732jD4TJfck2bEjkZfa4nScm6h2TIvOyD3x6VAAWUukZJnp/yp5fTLNlckpREq8ogHyO59WWRlMcul1yW2OV+ymOXS8qtL4ukPPY+JJcFJbmfQKkRK9T5RojMu+YkC5veVtTyFYskHME+tkpNqyeUbmdchJlde+G1gxcuHTS+Z7by/+gtTkUdWYuvZDrxfiM8rtW/JC4j6ZWP3JEs6m2u5EjVkrh1FJnKQtVq0nOkoJqUtjkfZWY5BUy/X6127yqSNqAoPUtthlLtCLffGdArKPS7fz19yQNniHht/doLem2w/u7CvDrYkr/l2BLiLii1qdz7MiNfawIrDA3ykKnlzCz/FiEeiIsifrq73m4NaW2Kc6Y0X5BGfgS7w5I09YGnfpmB3uDfClIdGq2Q8gSiO9uPpBBhOXQ9Sba49zvE8o02eJ5AlMQrzmWJXe5ni1wCSo0I0ISXfdrw13Kdw9bPZbGO2dGIQKs7V4v87GF2NMaiBVpF1IdOoNSIak8cmRz5Rg8XJJfkfspjl0vKrS+LpDx2ueSyxC73Ux67XLKF9fwjjDvbZmUlty6XlMcukYwws+71sq4Rf5uB0OUTLSa/659oGAYLLsrMHs2buQ3lMQ1F2fBj6gwQi5oIZLq1GCjnh90a6lYb9/OY7bk51q2hTrSBmZUkT7unF7deyTfAzEoog6HXfJL0aPWlS7tckkCkdkz04eewOiVraJKhOij7tMkluc5l4UaH9VOeSy2Q72Hc5X4OKwmUGvFvVRnkeDba1QLy5dngkvLY+5AEns2otrlzLQuezVHr8t7P/R0oNSJA9TP/COPODp2f3eYSmNnG3MgJyO9nOS04d1QETiEzG4Vq/nk4N4vdGupWW3QsjtY5N8e6NdSJtlZ3X/l9Wi4pHDJ5sD1Jtrj3u/VKvrE86x75GLVACaxKIwKUyrLP0CtjeYbIJeWxyyV7sZ6f5u5sm/kur5/LItkL8pgdjQighjRC1Nu3O/KcH1ZSXj/7kBw29j6sA6VGVPGtSSNE+vv+YXNJvrqQhNN2B4NcZ7coRZjZm+Vh/UNJjP+AwIIhsLm5uWAewR0gAASAABAAAkAACBwPAQmhozmd49nB1UAACACBk4YA6udJG1HEAwROBQIRZta9xMA18DaDFHEu3xuV0oD+4yCAPbMavfnn4dwsdmuoW23HSd3g2rk51q2hTrTRndbt6so3+pEMxiJ1KA+2J8kW38rmYXRn2+CZgiXo7yn2wErqkHJJ/jwmlkyZC/oHjz3wJ3UIlFLI8P7BUWqRyW5G5xtt5vuwNbkP63xwM+3Bxz3jGz81eLVpkZ+otI0ItLlz8TTItAfPkIxv/FRPM06en9yZTPuU45lBhp8CShyNVBsopZDh/VQZ8ksad3bo39mSVxuJJJhZngat2/LZ1Vo1LhAgAGZWgzT/PJybxW4NdatNkKFSkbk51q2hTrS1uvvK79NySeEgyYPtSVJyRyeZNquZU41S49OyFhh6zddHfrbIJaDUiABNeNmnTS7Jdcpn8WmWlM+jFsj3MO5yP4eVBEqN+NO9WJwhcslGu1qgp3VIH9blsfch2UdEw+oESo34Y242QoS3GUgg6gOlYzCz06n6e/cz+1MYwokSi9/5ptNS/afx6TbgznRPy0k5LSeT0vlnVPfhtbPRcQPMrAY0nocdg+2pm5vFbg11q81D5HgHc3OsW0OdaOuJSZRzEMKhkwfbk2SL1bb7JjnfaMPhnkCUxM/MyxK73M8WuQSUGhGgCS/7gJnNVyR9tk1d6qPOy0dTLimfm8siKY9dLrksscv9lMcul5RbXxZJeex9SC4LSnI/gVIjVmBmGyHqg3OkzGy1CpIsGF5tp1MSeNs30nY74yLM7MELl9au/8y9yuDDTz6Pv82gnEyms9l0MhrRz8x/0xh3yzpjp7U6JsT1m276YdjhWYYf5mLsgtwl3Fi2Hc8wjYy7MGWU9ysn3RXpxnQynkxn+l+SSiKvFNqzFUxMs5awIrPZTLk9nahhZXIErVXgGqqTCylnjFglH0p0fZxiZhU1rnNDs+QmzOm0dBkT+BIfykDIHjI9nn57PveTG6r0aFqcjUZORe0c1+md9NVW5jyhoxwkLcaUMbvHgkvpbq2Be9TK7RlHT5stjzpC3IlYu51jMQ3Cvm4NMW1q8tM/rRrkNZhZydi1W0eKVzN98BqScNque+Q6u10htV1Hyv0cVhIoNeLfbsaBmW2sOf3wrX1UMMyOxZ8djR5qAbZEabiiJ0nkUgPuegUorp/Acyg8G+1qgZ7mUR/WkUuNqA6/CmpcV2iBNmxvY9RHyORucynCzH74k9cuS5nZ6WRS0r5LxRdqam9WjidT6lcNTSJOSYDJKGZRd47G5bQiGonpHU/UVk4to08ZAUMdkn4i2KbleExMyXRSKVGbQElcuaSPnBhdaBVWlwgHKSoWr0HleDQejyfat7hR5YYLnOBS0Ri4JqNiXFr+1eN5FbD2zKycjIioNT+0Tn1tFBwuwNsmNO32aFyaUZgGqjRFq4axnIzVuBtJUqAVqoGelNNpaYZAK1EnndtRKI/UGWdmKQONuunEhTObUV6N6Tj2X3woY5Jcj6c/KlzrrAxxfxSdRZlak2cdFTEeMOOVTiZNTa6WmwvEqsOkiUpEtZIWAznyoYLdT9+6aKQnMNSsIYjAZoJWHWiL2ONdDD1tl58M21m7oXDtuJ1jtcvlHd0aqrSpr3SoVrVqKL/BzEqGr90KSbya6YPXkIQDZhYoNSJQlZcm0Z4ku11tk7Y2zw8trPcw3+WVYVkkm5LInG9XacWMktz6ski2yE+g1IgAlQbZp00NOc25BDybEUDWSSYdUBoOJfnqYtha1zzXNIayXDoWM0vso9pqWU5GxEUqmpA6xuMRdRA/RlSd/t1+JsM6lZCiPegy4nmVqtLQvDN1ijbmWv2MqDRElqb9tCRdVtK2T3MJEV1GzFxoFFZ2hcMZFSOQ6/9pS8qtlFHeb3arKjenkzGRuopA5FEbIy5U5z4Fq/5TO2ndtS5qd8VEUb1OgBsyypnb/tkKZ+WZIV80V0WSigYfVwOtOvQ/VSzj8WTcuL26jmW+J8rMaoZZs/YGZxOBQyWiNT6UEUHVZRWG+lPyrN8zZPWo82astKw6MOS4apOo4vLVnLPMuBb2dDJboVrPnCHT2dcAOROB1qzFQJbBPqUk+P/Ze3tWWZIuPfT8m/sPBOVcuHZbgyxdOcc4JMg43kXu4fhHk8gYhGjoNgVtysi21O54jV5jDL0JAjE9emFoBmYMtVmXtVZ8Z3w8sSuiclfV2l19KjJixfp4VkRk5pOxc/OycZApVKSGDhoMapwJAU1qNlqA+AFNoDnVFjQVika9PEcK95N32S0o99X9jvm+XaWxhrw2Wg6YlO0qsOvKzCIZ7OMLJjA1iJPz+Fbc+tgrJNKWPcvnHHogSUUpl8Corm/GIbcunWOpI0cT5jt+R/QoklF2ywen573sWtRy+mrTMT4nzI4Ii/KBolTGxrc8JUr4+PRAVEuno1T1zjfqCuaxKJcUpTI2vuV0lPCrC+90tTRpFuOrDSJ5CzNrNvgle2bNrlUhAmlDp/Ctm+FIhMrylcTThBsZhVvhjbOG8rNbOA2BaahA2pBqeCZmMJ0SOrK/8O8oGt6JyEaJP+RttondaiqLjfkcM/FMjKX4yMRlatQ7Q5tlDSVNnCejypGF1A97QKERQ83Et0BLO5MvTJUK8UqsneQlA06inPZnGilWH7gdSjoh275IaCEzywEEid4oPJMSb8IEVESzv6HAzPLOU7abMqfemdRYPpWplD22elL9tr3yHRmyevwDBNuTUuB57ctl4c3M9kmF7E10G2wjnVaDfAcWXCaNRJeJWCvdYiY1tUPrBO21Dl/GUetj2hJDRw3hAwyTDj8004cBibamfeu4EQxHcJfdpqFex5oKSwJjDVlt+0aMu/kfLvCvFejbDEqpiuv7rpAmMDWxO8UjOySKAq5hkiRy3UMyZB77wGvdpIgcYvVCl3U8dlyy7p5r7fLT9aoXJunEY8cl64G41q7xid+9vLKkw7Ze6ENe15AmAjQ5sY+utAhQihKGko66NgI6N3UsVU+Hp58N8SuWahy+8SGuFTPM7OcvH7/7+PXzz/5Vs/n3zPpI314KmY43a4mVyO+XN5TFXRrClWY8x/b3/Y/KDJtkX/R6FHA1XtJsEHYt5cKoSMsWzmzJMrPyMMBS8MQXC0lOrw0l2j7/rtCOVAZ6iNx0+jEkvKFIj5Du/g+yheQ4J9ES4/zeC3724IW9ztgHy+WzZGBOpLpMxIp7mNnALlukzfH5HCQ2+DAJ7ajBjHCZHP6BB++eP7xAI9GWM+jrQvTolQy8q9+9HaHLrldaKHU5VtABVY815LQxGU456CqIx3Tun8Ak4joh4JhBPleyfZ0tV5lz8Dw3dtx6B0rIRXnnPkfcz3MlFaUm/uffk8DjE1/rXlmymXEROD3vuJ/nSuoa0sRfx1ITIvOXBvC1boIk4uR7+H0g3E+dm02sdG42IZo3NxHTxjp8b4jrnCE5dsZlmNnwb39JeR4zCwL0bsUcMfFuPXxux/LM7JtivlsqZxiaobOO4t0sjjU0Vlsdoq7Wuzk21tAQbXSFBJ99Z0iCmcKDnSTZce6fgOcTogTf4z1K7LifHWNJUWoiQBMe+/Tsd8N1zlgVn0+nzo4mAl1nro7xOWF2NGMRga6IZuhUlJqoTuLIcOSbHr6TsYT7iceOS+LWH3dFQiEAACAASURBVEUSjx2XfJTYcT/x2HHJDuvwvQyuc4YkHjsiqcwsmKO8GH7Wz/fX2tsQUGZW8Lv/OLybxbGGxmq7bfBGve/m2FhDQ7QpMxsNhcJB390LfDWD8y8Fv9JqfEhMkkSue0iGzGOfHjYthaNwPCn2grW0uit2RamNwJyx1LYrA/jsJ1v4GnKuZDoNCsc6OwrARNWKUgRH4UBRKgATVU9CCV8/I2/KB6eftcuuRS2T8IxslA8UpTI2vkVR8liUSzSS4XuZspqoZRLy+GqDSGaY2R+2X48fAkh/FIF3hsCnT5/emUfqjiKgCCgCioAioAgoArchAD85uM2M9lYEFAFF4OkQ0PXz6VKqASkCr4BAhpnVtxlEBHv1AGffq2q08Y0I6J5ZAe7+4/BuFscaGqvtjaM21+1ujo01NEQbnWjh56IzJHMJydThwU6SRJ61kswcPDOI5KomxZ4zlamj2PH7MVgyYylXdXrsOacydYpSBpRD1ekodYzkU9fPGWvyDJ2HDOcrTs973q1D7emrTcf41JW2iUDPmeswFvIVp4+QvFuH2kkzDh+fB4/yFS+OZx6UQ62idIAkU6EoZUA5VNHKAF/bHHrnKyYhj682iKQys/nkgbV4jkGFKtaFgDKzAtf9x+HdLI41NFZb11itC9/NsbGGhmjrOvvi52lcsp4a14oHO0kSOaOTTM/VzEuj1LxbFgF9mwEClKI0GqVz5zu+MjyKpFvJ6wVaP5FU6htRFKX6SOK/GqpjqQUST6QJYwlHvumhCEy6rpthHY8dl5zh57k68dhxyXMjmmEdjx2XxP3Ery5wnTMk8dgRyRuY2X2XP1Nuv8Fgn0osv1Lv+0Y/Bp9bAx6r7eiNzZ/9Pkq83xplZiU3+XE4M293szjW0FhtAwG+m2NjDQ3RNolJfJQzOjiK+vgC+DnzS6ME3w3iOXoUSeTqkGRohmMfZWYRoHpQwpHHZ/ErS+JzswN5JOlCPWHm8VPq6ZKKUjOlXesnjmfTrgicPkJwP/HYZ0jifj6KpKLUzJTOzSZE13fwbAm/YkHCkYhmSI6dcRlm9vP3P37++PHbn/5wrzX4Yfs1E8m2rvv1uq+XC31XfvYc5xdU5ppFXSAU6jfV9OXYT18KJakcigUduCGV7T3On/kEGdblDfpS20gkG2hzPY0AfXl+3GbBVjnpQ8H1ohajf1+Xch7DDkHZFW2Bvq0b3mq20jffUMozs8Jlez/2gCQPy5HhfCojEX+wezWGhfdtrVJoyOsRNZt3uqUmag91Rg1ykAKSEemtaliM1fkwrzfAFUbxVri63DZBhHbjuAYevcWxN5kfayjQxjOf/ukqUAx0hTSBScR1gkAGwTZ6TJLsOPdPwLMRs22eFLtV3/jWq+0GQNysKD0ESufOd3z9fBRJJOnv4V4U9/NcyY7xqfx1EwE6cWKfnqc7544Q3Doe+wxJ3M9HkVSUmpnSq6AmRO/hbIhfXSDhPDAzS4Tsz18//4wws/u6btu6bsLqCce3LetO9VcqXJnw20kgkAkqL8u2h6Qgl0mlyEiTEWD9Uk9c274tC1FZ++qVUE+2yS7JkRMjx6xC3wVMZ1YsfxfquFQmKjnubV0YKPJ2WXcf4Hr5sIjHuyVJfS+2uS2XZVkMIBIRSZAajwAfEMg+LpFA9S/L5SJ53IMu3k/BjVy0gQjlvS6mF6d43cineDwk4WRxfGtliZklwnlZNsFvJfTEwhaUE5v5VCZCckjpM9p5oEtOs6KZSm/ooCcjHVURlFGFPfA6bU30zd0cIFGTPwiUB0XfHpcaFkPhKExKih1LoVCx7A0FUQjsaZ+j21QTQea1pZ3Lx6yghl5gI7VX1pq0vMWxRAV2ONaQ17avK69rtPbjBfZZmVkkdX3XkcrMNu9yaexiH70TRoBSlEajhI9P/O7llSWRZfY93Ivifp4r2TE+kamhO4sVpSYCPWdtfHyeO49mWMdjxyVn+HmuTjx2XPLciGZYx2PHJXE/8SsWXOcMSTx2RDKzZ/a33//87cvXn35vM7PCeBF7t16IPbzIrkuivy5UQXswibDj3+0PZYJKFhIil1kzI7b5rZxMtXr9jvZ05JsheoStYW9W4oa5CzFyhlQxHVks6gJmKSfmiYmw1bq4U0T0v7AV4qBzjFqlnZhZH6DvJTq9NhNRIOBCcyB7PDv1EySUucSlOBFXpl1sICY64txNikVFNB4Cb0OMxpTzzCwNOhl9xAISpy3MbFg+2M+n8iBmKhxRt6/L5eKY35J4WB8Zsnrk2QXvQjeyPEQjlpyeQ3CWzOi1AwN7CmQ6ifaK8oh8D/2Oy1EUcVPmyIZpXLaHGclDVWzIRFGCS5r5X3mGQZZCMjvWdjCWrwiGEwsYJzgYLpvnPRsNOn4klNdTq32TYzWFpbaxhrw2M7nkqZxbJloF9lKZ2VKywnplZkM0SuU+lJr3gSKgnCMClKI0GiXkCp5kzv6dA/ze6VzJ0qKR1OsakgCSPVSUsrAklYpSAkj2cBJK+PqZ9epY6S93j21xzemSeOy4ZBxi8ej02IuexQ2TRl1spHikKBWhCRooR/Auk6BfrTgJeXweIZIZZvanL1/DVxn89vsfhbcZmG2DzIUaFnbdiVElptFsXd2JF6V9tZthLISb8ZVEa9kNiISmMB28r5Q6EunnNtlZKoTqiW8xBA/Tmk4JHbm9urJf1ToaKkzt1jJZbsvn2PBPwkozScg8oRCELkDiezYTRMj1cMzM54pdPt42oXxIkJlQEbAUVw5PokQx/fwWA9J8cIn9YuWcCNqjy9hSUryf3jqlmvhaxl3IdS9WhvHNLQVmlvSRXWLM+JGB2UnsyhmD+VRmBLnKAb8S82fSVxKO6yNDVo+IhHoOxPqF9wALAeZ5fOkY6YzNyVFshxyOKXivPCTfc5pMXdNi1NeaNzPDHkYyhYPQUNIvhMtoNgtP+lTG6Q61uUqkwMPJCIbPUUK7Amvz7S5Zc292LKutUjnWkNW2b/SAwvwPF3gV17cZVLIVNPVdR8JXM49y3RMgUSv2oYRQabqTS1FqIkDrIPbp4a9xnfgsfmXJ2sIRtOkaEoBRLCpKRWiCBkUpAKNYnIQSvn4WPYsb7OVuXJs7Ol0Sjx2XzAWaqTs99oxPuapJoy5nKlOnKGVAOVRRjuB7mUPvfMUk5PF5hEhmmNnvPn79/OXr55//3HjPbD7qvtqQW+nrGUjHSvaVGaygPVOMu2QEwCo8x6DCG8VGxXWjG3frnmVmD1ywUOLiVFiO3OxI5b7Tzm6mlZj+ZkI73JkZKU4PvKFQjzzf4Acc1tGEWLdhJe++YGmvM7VGx8QkyhsxbOuBtXfKI/Ldime+6xajDmGY9EBB6P1IpHLgDIVR8OtAgqcXsjM+epAjUyHhcollqdjKNllo/FuYzSwTUpYfS8gDJPNQKkhiVmG28g2OZfU0K8cactp4XhEiXQXxtuvsi5+ncckmaM7PcyWRMzrJ9FzNvDRKE9i0c0cIbr1jLClKTQRoHcQ+8AmIZjGsE5/Fryyps6OJgDuhI5Id4xMeyU27ItDl57k6FaUm/n1rHTyWcOSbHuqoe6AZh2cTHyG4JG79USTx2HFJPHb8igXXOUMSjx2RzDCzjpB1hfyeWTC4pxbDV6unhuG04LLM7Nu8uVsqZxiaobMO490sjjU0Vlsdoq7Wuzk21tAQbZOYxEc5o4PjpO/uBX7O/NIowfd4eI4eRRK5OiQZmuHYp4dzVJSaCHQhj8/iV5ZsYi4Cfcjr7GgioGtIEyJdaRGIOlHSM1cbAZ2byMBTlM5DCb9iwc/vMyTbc00wxMaSMrNgjvJiBLL+nIeAMrOC/f3H4d0sjjU0VtvAgX83x8YaGqKN7oQnMIm4TjCPeLCTJDvO/RPwfEKUkMtNvht8lNhxPzvGkqLURIAmPPaBrxj7+MEJ8x1fPx9FUmdHE4GuMxc+5nHJpoci0OXnuTrx2HHJcyOaYR2PfYbkjIjO1akoNfHvO8NOOL83PRSB09e6c8cSfnVxLp5jUcowsz9svx4/NIj1RxF4Zwh8+vTpnXmk7igCioAioAgoAoqAInAbAvDd4G1mtLcioAgoAk+HgK6fT5dSDUgReAUEMsyse4mBK+jbDEpkPP40o6RB629BQPfMCnr3H4d3szjW0FhttwzdpO/dHBtraIg2OtGeuucryUXpEA92kmTHU9kJeJZgSeonxZ5YKR3SWMLvx2DJkrmk/vTYE39Kh4pSCZmw/nSUOkbyhPl+7po8w3qY3Er59LxXfAubTl9tOsanrrRNBHrOXOEwqJRPHyEV38KmSTMOH5+hM5Xyi+NZQSZsUpRCNEplRamETFhPKwN8bfM//tPfIJ8PHz4gYv/jP/3NiZLKzIbDoLuMz65u1doBQECZWQHp/uPwbhbHGhqrDRihqMjdHBtraIi2rrMvfp7GJcEk4cFOksTvNPDYccknRKl5tywCPb+Brig1EZg0O5p2RaDLeseMmzCWOqzDdy/4fH8+SXyEdCA/Ie+4n+dKKkpN/Cdxjk27ItC11p2rc8ZYwnWeG/sM63jsuOQMP8/ViceOS54b0QzreOy4JO4nfh3y/vlWnO3NMrN/drtlpZDfM7vv8ufo7TcI9VOJ5c98+77Rj8GnEbCBbxqK+7ZJnhp+PGSzMrOStvw4nJnSu1kca2istoEA382xsYaGaFNmFhlIffd4E5gaxMnrlV7Leq4kfnWIS54b0QzreOy45Aw/z9WJx45L4hHhOvG7l1eWnIK8MrNNBOiUgH3OPnfgIwSXxGPHJXHrjyKJxz5D8lFQwv1UlJpY9V1R6wrWRGDOOo9fsTw5M/v5+1++ffz47U9/OH42z8xu67pfr/t6udB35WfPsY5BZa5Z1AVCoX5TTV+O/fSlUJLKoVjQgRtS2d7j/F2oIHPQ5Yy7Aomw8L4um5HPB2K60JcL+WCAKxKBbV2WULdNVSJmcIo1WBn6tv280Wylb75LqczM7o4Y311RCPMCUZ1PZSEKUGe2d2joFj2h8lBnWH+VhwQmeRz/MZFRB/SgaDGnwId5NQ8tclL5Om8oioUGrEux6blvayG5TrXX5qqaheqwafYGBbodS9EA7WSIsyA7qBIn591+qz/C5eFn3xmSLpx6wQdbl5vGTnZcbSsze9J1ZGtomPZHGktNJEVAWRUEqB6Uzp3vM1bac3Xic7MDeSTp+lcEFaUmAnRKwD49awg+5s+VxGOfIXlu7DOsK0pNVJWZbUJk7s7gdQkfdYjp3nvDJ2dmf/v9j7/9/uvnnxFmdl/XbVvXbV2InRVGclvWneqvVLju1LSTQCATVF6WbedDkykuk0qRkSYjYElMUrjv131bFmJi9tUroZ5sk12SIydGnliFvgs4RLJi+fsry8xKCOvlwyI+sdtS6UmlbbksC8MXBZLtG4TMIHvNFnwmUQVpdliSIdTsti6cLEIsTIpHezP4uHxJYd32fVviLKeGsvBMrywxs8RHr8x179u6GmqaB2XRpXwqs+Kwzmxvb6hbT5EM9zoTk0yp0wS4XuXf4BlAIiqHRROJdNFiIscMapAC8oSH31EuX+MNBbHwEw2bYtePppJ5wGHD4GHqBHooM9cpO2wSftuakwccrmtHwYcJduJnJZJTsIeIpYaCQZjXE8eWPKLx2pr+lPXontk88nFt33WkMrPNq0kau9hH74QRoBSl0Sjh4/NcxvNRrMcLavGob6VFkq7MrKLUREDPR02IeB51rIqIQp2bilITAZ2bTYg652bx7Bs3dN0bPjkz+9P3X7/7+ONPv7eZWaFGiNhbL0QvXoRgJFrsQhXC1i4r/25/KEO0qalkISFymU0zYpuhea/cRBtzrX5LexI5I5SbIXqEQWFvVuKGuQsRNUbMdDQKvd14JPQdeWIi7Gdd3Gm/KlHSiwvHMqhenIWJ93SMlfXw2NfFEmoOwaF6smd3MRNXta6SmH1lWMhQgL9Bybrsm4hJdzkSpjPIQmrIx3PXUp6ZJQBlNLAzlr4yNLPFJnE0n8pEyB1iOp14WIgMlfUcqHkS5QcL8tAiGkmRztAYlc38IGLePpkQkS4TidaqxUTWDVs7qW3UB7lMRWzIxMLLQpBiCZKHNT0D8g8ezEMFR6TG2jLmjlWZYbOtvNSZL9mVT9MleER01FOv6XeMd8MXBnPFVsZQnA43XNxzNanZaFnhB16B9kBb6g+up+vsO4MFCAKqFYNga2LzfqO/455EmdnmpSSlE/so54gApSiNRgkfnzNWxefT2Vi1bbMysxaJ2reiVEPHtilKFona9ySU8PWz5lzQdvoVYOBLrTgJz5rJoE1RCsAoFhWlIjRBA41k+F7myZlZeonBn378/L1/22zhbQZmKyJzoYaFXXciX2iHqNm6uhMvSvtqN3NPLxSgr7wwdWi3uhkaiW/qWYb4joBbErKAOBDaLGsYBaYmg215/HoFVuEoBd5JFylM7QaDoaOYn12W5iT60m5WZCqT3HYFY0aEeStjGEi2bxBypFkocAaft7ZaZpZ3LQs3twhfa9gsjz/vvTWdGFXbRDuSXeI2Ogh3PRsSzBrqgGyoaI6Z3YmJpmcDvKHaM/PGsCGMDm7kU3kQMxVZMqskHNdHhsp6aABYWp8HhuwHpQSGXLzojnTG5kILtG0x2FDdZSLWSg/IkpraoXXCzAx7WOti20JDtt8hxUJT2zlPD4Xihwq3MLPiSIwb/6bAyj/8awHyOMQscRFjbMNofYdhtmR9e0qU+pZiKWPIwip9wtFl8iUR8XBJ3l2TaAv9wfV0nX3x8zQuWQQrbkiCjRujo0mS+J0GHjsuGUVYPpgUe9lg1KL3JBEchQNFqQBMVH06SufOd3xleBTJKLvlg9PzXnYtatGVNoKjcKAoFYCJqp8SJXz9jLAoH5yOUtm1qEVXsAiOwoGiVAAmqj4dJfzq4smZ2c/f//gZec9slL43HoR8xxtVON7W9G/9ujaLDbHbtTcKiW6UV4it55DJMbMSmaXH6E0alwsT+fR727z51/F0IQj4SZde3orpDPW7sjdU1ZNQ87Jdkdw3b8aA9swSO8Yvy6DHG+bxiPl9f0PYB08O6iac/1LwUSQNx8MwTN4X7/d0H4UPNc5QGAtL2RRLF96yaWI9PFRwMTttBzvFiuOwYSZzWy72rS28XZbYYNpU7h4RFRVmG3ode/OjkdRQkB1xzKxCQsoykvJ4zDxyix/GOG1Hf3A9dO6Hn4vOkMxm5Fjpgj02JTWTJPE7DUWpjRUlCfvAT6Em5T0ZXaXDLut47LhkybGkvsvPpG/pcJJOPHZcshRCUt93R3Tq+jljtZmhM0G4dNiHvK4hTQRocmIfXWkRoBQlDCUddW0EdG7qWCqdCLn+9LMhfiXw5Mys+8NfrpDfM1tN54s04vcDLwLIncMsM7PdjtwtlTMMzdBZR/BuFjsMAU82OrTV48+1AvZz3bhuqmOh1bGGhmhTZjZMUKncd4U0gakpOZbU40NikmT7bkSuxck89tE7YQQoRWk0Svj4xO9eXlkyWalKh30rLZJ0fZelotREQM9HTYg632WJr5+lpSCpn3TFklgpHXZZx2PHJUuOJfVdfiZ9S4eTdOKx45KlEJL6SRElVkqHXdbx2HHJkmNJfde9oTKzCXqve4iP79fFaGbkD8fMyoCh5Wboz/Dt282k3W3kjzU0VlsTJVzgbo6NNTREG02FCUwirhNMEx7sJEn8ugePHZd8QpSQW0FlVRSlJgI04bFPD3+N68Rn8StL4itYB/IT8o77ea6kotTEn65t4BGCSzbtisCk65AZ1vHYZ0jOiOhcnYpSE3+dm02IhFg4dyzhVyxPzsz+y9/8q+NnKI+kyhSBMQh8+vRpjKJ7aUGWwjfL3CsItaMIKAKKgCKgCCgCMxHAOZ2ZXqhuRUARUAQeDwFdPx8vZ+qxIqAIfPiv//3//Jt/9x///h/+8r/+/n//wz/+019+/+cP17/7D8nnX/7mX72ZLXrujvgzyefG4azodM+srGG6ZxYcge92wt7NsbGGhmijMax7ZlsjmFDC7zQm4Nly0LTjQ2KSZAdKMJ6PEjvup6LUxKpvxk0YSx05mjDfz12TZ1hvZlwETs877ue5kh3jc8LsODd23Lqi1MRq0ozDkW96KAKTrlhmWMdjxyVn+HmuTjx2XPLciGZYx2PHJXE/8SsBXOcMSTx2RFKZWTBHeTF8pc7319rbEHhcZva2uKPeMgjvPBTvZm6sobHaojTcdnA3x8YaGqKNrstPZRbA1OHBTpJEzugkMwfPJ0RJ+YImAjSUsU/P7+nrWGoi0MdWnLp+nrt649abmItAH/I6O5oI6BrShKjzDar4SH4USfwsM0PyUVDC/VSUmljpOt+E6LHeZoCE07WJres+buyMu4GZ3Tf62bN/6B6E6HSxXYJ4cxz5zBlkguj2bd34b7wHdfWieIaim9Pfp6HuzXttVWbWLTT5oTgtcXczN9bQWG0D0b2bY2MNDdE2iUmccccOZhyHpUuy49w/gak5N3bcegdKyA2zvmdWUWoiQNMY+/Tw17hOfK17ZUldQ5oIzDofTZgdzVhEoCuiGTo7ZrGi1ESgZ6XFkZ+R93N14rHjkudGNMM6HjsuOcPPc3XiseOSeET4FQuuc4YkHjsimWNm/9vyV//Pd9//N/9Og+zbDHZmDff1smxRmLs0XOnbFK98YKRsXdgcKYikwxajLupotYVyUg7FTE/XEElvi4kgknKylnnOtF7ppi3SZXtdr+bvtNte9J311dbGzeTTzkCQRisjRWtD8DdKuXvI43ZrcFZiTzLhvaOqMjO722cGIU3OZZvQJIx8KhMhe7g79derKC1otR3st1iJbBkG3Ur0f2d0BkoCV0MoAok3FaMQWhq8D+ICjW30JzI0CCvQtne7M8ug/lAsCjNsGF0eayjQxisR/dNVoPCUmUWS3PeEX5nZofd4SILcQzJEOJg4DfFJksjVIcmQeeyTvRbKBTcpopypTF2XdTx2XDLjU66qC3n87uWVJXMwZ+r6kNfZ0URA15AmRLrSIhB1ojRjTc6sF7mqrrNMTkGmrksnHjsumfEpV9XlZ05Bpm6STjx2XDLjfa5qUkQ5U5m6Lut47LhkxqdcFZ2L4XuZnIJMXVfsmf65quHXDBlm9vt/v/zy1/9vk5kl7pF+Lpd1ZxpyW9eNC8RaUYF2iS7rLiQll4nGFWGiOoR9lDATDXxo2c1t9Uroxt+SjoE2ss3ibFGOnNiyij/kSeCAxZfkDJMqTi6r2d66rcvGuoQcFadsN/7O51iQIafph5AgHPb18mERLw0mITLrtu8boUU/4pJYYqspeqxUkHQ+G/3S620ayE/KInkS+CyBy7+i/r38W2Jmt3VZVnpisNPAMAPJJTp+lGBiyacyGygND0vnu5xlJQ+VYiWyxXx6mC9yO+5Iw8jU+JITyeh0bYGrIRS+3ZW4UDcUykYhhA3H8sGHo0ilJjLE0SdYHfoGQRzaIm2H1qgicPsKZblmN9KcO+hwLNcdrxtryGvb15XXzb2rwH53nX3x8zQuCaLng211mCSJX/fgseOSraBN+6TYcesdKMF3g7j1R5FUlJqZGn61TZj38NcdOYLvXvD5/nySzYyLwOl5x/08V7JjfOpK20SAlgbs07OGnDtCcOt47DMkcT8fRVJRamZK1/kmRGbfDLwu4aMOMd27awfXOUMSjx2RzDGz/+U//E+EmZXghDhcL5eFuComUakhJPOI4+M3HzDZZ9kySz8KibYlGphG2qXyQoSl0+x4S8MUCuFEBCpRA6YLcW+GwDEdjULmPqWLTY7IBU6aWIjVI4WG2luIjTPMqe1KF9qunBS2RXowR8gkttB5RWQYiCMzGzjmnRclYdMi5izpGLJXoRgFEEDhmtYwR5KS2OdlZQ4+CfLswzwzSwHaHO/kt7C0RLRbjv7oeCWVR2E7uK7bQgM/fMaQEQ6qxEpsi+CORta2miHPXwG/n3mu4DZqxToDk24oBFCY5k5DgdLayA/FrCFDZMtjBHrSAv8c4jLzXhTwQfjMg6I1z4X4sVC4cDisUOMWumOWe+02LR7CbPZ4o8BYQ16bmXSyYrqls1XgIOgK6VRmAYTSB9vqMEkSOaOTzBw8W0Gb9kmx49Y7UIKvOHHrjyKpKDUzdfqdW0eOTl0/z129cevNjIvA6XnH/TxXsmN86krbRIBOnNinfNeZjIfTz8WJP6XDSTNO8WwjoKMOmXSK0nkozTi/lxaipL5r/WzPNcEQG0sZZvav/u13f/Vv/++/+vf/3//8O/NCg+zbDJjUWxd+mYHhKXijJf1jN8YaEoVIym2jD5FkdruhpT0YDKeBdsTyfk231VG4FdqHypod5cokrNNGR25rLXMyVn+kMHTAZMHIeSd5f+uyCBErDJ8JNuLPqHs2c/TSVyY3me60zOxmHDeBEHA7EXwGGfqmA3GKSDTavrpGMt75A7DMfNmISUenBoFdHBdPDLJep7FpUHsfXzlmliOnvdwMMLGx5jkBoTKemeVXYXiUGrjIgDkOGxpglq6kIUePGfiHnReO38hYztlZKuk0AtY3JqY9FDxG+gw5i6WRHwpEZeuDVHaNpASrWBOF455J8IIgL1cRmpAfsQi7bb1JtNnqwrc1Zr7toUyvLrsFA766zzHfr7s01pDVtm804cz/cIGWNxlL+Nl3hiQIog22LT5JsuPcP4GpaYfNEpNix613oIRcbjLTjVt/FElFqZmpSXxB064I9FmfMN9nrLTn6pyCvK4hTQTolIB9lHNEgFKUMJR01LUR0LmpY6l6Xuy7DkHA7Lyixq8ZqnH4xkl3KO25JuBgMy7DzF7/rmfPrI+3XepiZJrqYm37mrzvNtc/7pKT6KzDc3xQfCDYDhJJxe3O364hcen0wxwzK04ZeIm5Y5qc+FlLPGfd7kjlvtMzBqGVAt4/qzapFCuhrSPpzwTg3P0CwQAAIABJREFUtvBbQlbah+6eeHhqPqs2qaTDwNUQCpF8gyFnIgzBVeYLoQ+8tz3eIZzv5GpDQ8S90h5l+wCDH0DQvOdIeHhbtOxrQ96+ZzZwW56gUB6sWwxmh13br/gdhlkUGtEw1pDTxvONfj+hqyAB0bn/VGYBxNUF25SfJNlx7p+AZzNql81zJTtQmnAdeW7suHVFqYnV+fck8Pg8d/18FOvNjIvA6XnH/TxXUteQJv46lpoQmWfz+Fo3QRJxsms/yqQrQNxPnZtNrHRuNiGaNzcR0727dnCdMyTHzrg8M3u1u2WlkN0zC8b23GL4+vvcOJwVXZmZ7fboPqkUK2+zlSXW6ezCj9BdoTvyQ4esoUTqbSEkSpDDsYbGakP8B2Xu5thYQ0O00dCdwCTiOofnCIelS7Lj3D8BzydECb7He5TYcT87xpKi1ESApjH26dnvhuvE17pXltTZ0URg1vlowuxoxiICXRHN0NkxixWlJgI9Ky2O/Iy8n6sTjx2XPDeiGdbx2HHJGX6eqxOPHZfEI8KvWHCdMyTx2BFJZWbBHOXF8LN+vr/W3obA4zKzQqTe+K95pjSamUVycreRP9bQWG0IUKDM3Rwba2iINmVmkUFCKDXvW0RgDtONOPke9pV0oATj+Six434qSk2s+mbchLHUkaMJT2LwO6JHkWxmXAROzzvu57mSHeNzwuw4N3bcuqLUxGrSjMORb3ooAvjl7umSeOy4pKLUxqrnyeuj4NmO2t13TFjn8auLc/Eci1KGmf2Xv/lXxw8tnfqjCLwzBD59+vTOPGq4A64doNjx9N8wr82KgCKgCCgCioAi8P4RgO9z3n8o6qEioAgoAndFQNfPu8KtxhQBRWAMAhlm9rff/0g+P2y/glTRq4kdqbFXQ+DceHXPrCwD4ebZ+2TkbiN/rKGx2gZCfTfHxhoaoo3G8Kl7vsA84sFOkux4KjsBzydECb5ze5TYcT87xpKi1ESAJjz26dlTg+s8d/18FOs6O5oIdJ25OsbnhNnRjEUEuiKaoVNRaqJKV4DwCJkh2fTwnYwl3E9FqYnVpFHXtKtjqWtNxq8uzkV+7IxTZhbMZl4MH2H5/lp7GwIPx8x2/bYvgo0yswhKTubdTti7OTbW0BBtysy68Vkp9F1HKjPbvNOjsYt9eti0SgbDJnziTJLEY8clwwAr5UkRVSyGTV3W8dhxydCZSvn0+Y7fET2KZAXtsKkPeV1DmgjQlMM+utIiQClKGEo66toI6NzUsRSe/A7l08+G+NXFwfd8RdcVYF7FoXY4Sjcws/u+s3/2++DsC1Tkc7xv9CPojAZhZ+UG+lHKRek2WOso7yp6lJkVcPLjsALczU13szjW0FhtN6PoFdzNsbGGhmijs9oEJhHX6dNQLeHBTpJsX2fLVeYcPKvY+MZJsXsD1dLwKyTCXO+EsbuXamZ84wPh2THjEIg6x1KH9VPXT3ylPVfSD8FqSdeQKjymUVFSlOoIdK3zHWsdvNLiOuuBuNauiFyvemGSTjx2XLIeiGudFJHTXy90WcdjxyXr7rnWLj9dr3phkk48dlyyHohrpbMMfG3jetULD4FShpn97svXz1++/vQn/06D/NsMtnXdr9d9vVzou/Kz57jboDLXLOoCoVC/qaYvRyb6UihJ5VAs6MANqWzvcT7H5JT5+/bOYAIROxX7VrDtNFD7tizE+EqwRocJsRxppMFaiSolldwU1Vvh8NsLUCkJi8Em6Vyb1Ia6bi6XmdldeGbDORuevEaZ51NZ8HA36q9XUdlDw4eGbtETuhbqDOuvhsiXOiH1o/Y3HxQt5jT6MA1e6bDJdTJ1xlAYSFiu9Mw1dbkdo0dHh/Ges/Gmuj7HeIa97fHPwVBtUjRDCbTxYkD/dBXIQtfZFz9P45LNMEUgCLbRY5Ikft2Dx45LNmK2zZNit+ob38oXNADiZkXpIVA6d77jK8OjSCJJN+cjZX9aYOka0kKI2hWlE1HC10/Eya7fd9SrIARSRUlRqiNA66cys//4T3/5/Z8/fAs4WXnhbJmZ3dd129Z1WxdiZ4Xg25Z1p/orFYSh3EkgkGHaUiovy7YbFpNTxGVSKTLSZARYv9QTR7JbnnL1Sqgn22SX5MiJkWNWoe9SHxn11vzKsq/LsnDwRFBS3Nt6oWP7RY3soA+BQbt8WMR7ByYznIKcIWatQwTxvm+LgE/qNquNMrFwXixHuhoxm6NYrUmcoZOzyTp2ZPsErSWho+6hb8e+Noabv0vM7LYuy7o59ezmlQel99a1SiGfykRIDvdtXSlwQpfGW9+PN9Sth9KWNeZ1Js3cQcK3IIjjiZw7LJpwElIoWkzkCKMQLrJupvNRMldjDAWBCPUn4bgeCS5BGBFmHW7z3PGTLoii16iTrxT6HEt8q+g9NCWG6pOCesdQJgPQa9vXlRY1XvvxArvXdfbFz9O45AGkfIUPNt/uaydJ4ncaeOy4pA+vWpoUe9Wmb9Q7YY9FuaQolbHxLaejdO58x1eGR5H0qa2WTs971TvfqCutx6JcUpTK2PiWp0QJXz89ENXS6ShVvfONuoJ5LMolRamMjW85HSX86sI7XS1NmsX4aoNIZvbM/vTzL9++fPz8c3vPrLBfzMxeLsuyMPvItOByoQpha5eVf7l/W70MsZKmkoWYHhA2zYhtli3kJtqYa/UH+zsNOWOIHuEY2BvmB7gL0WZGzHQ0Cr3dahIbjZUcbwuR0fI/ObWt5kc21C4L7zX2IRCXy3xfGCxxvKxFiKeQjaKoGTKivBnM3UZKfKFhx4kFsz54DF2l4bMspkFeQuGw7PzhPuwQa6Ou9J9Lq6QzSFxqtAEt1JxnZinFMhpEiYVtX5fLJWRsQxuVVIZipuxUUtyEdkamUBUZKuvhUb2vnqwnUeb55aGF5bvZSqQztWvmB3P3x6cgqIlEa9ViIuumoJ3UNuqDXKYiMGQCYaGwTFCETz5kxzbPj/QBTKAtY+tQRYOYVwpuSdyGjR7UZio6HaNlLfItozJflRo6TAo3XNxzNamhBU2eJwWKvTYz6WTdcQtQq8Cq6NwPPxedIRkEVCv6YGtS1DZJEjmjk8wcPFtBm/ZJsePWO1CCd8bh1h9FUlFqZur8exJ4fM5YFZ9PZzPjInB63nE/z5XUNaSJv46lJkTzdhbj4xNxct513QzreOy45Aw/z9WJx45LnhvRDOt47Lgk7id+HYLrnCGJx45IZphZ2if7px+/+/KLbJj97fc/CntmzbZB5kINC8v7QnnXqtm6ymwh0ZIbUVhuKyjd5UslUWV2AyLBxSwA/8MyRK+4TXZMBhoekH5/3DAlTGU6Jeb1Cl6PFaNv3mDKClO7YKoSsexd6C7REmNnyVOCalsudjOx3djruFQKajMBCQ8iJBZTpcStGuaPaBRmAg1HJzgaMK022jrLrApB5zSE+LvKhJkViJJk5fxZmBXaiEanmMgBdsJ4wvqpJtwonRpNoHzTYY6ZZYyI+OYXP7jBw1BsZhN3xlg2lRk5qYpJOgNRUTpqiAyV9RCqQoPTruTLZbnwZlchwDxXLqojnZE1N/qplrY/ug3YjAxuItbawT1RRxumeQRgDxOd2UMXWtgpLPOiET354AHJg1KCDVh6py1rK1tpJk4QhYiR1uBxS8VoVm1S+QbHhJ21S0Oir3iYGGK+PtrFHD4ZMvkSAHlEJu+usdr2jSac+R8urPIWkElM4qOc0Yupihv67vEmMN2xO8UjOySKAq5hkiRy3UMyZB776HtmEaAUpdEo4eMTX+teWdKtPPVC18qA56hu1LVOWhWd/nqhyzoeOy5Zd8+1dvnpetULk3TiseOS9UBc66SInP56ocs6HvsMyXogrrUrIterXpikU1Gqwz7veUDTrghMyvsM6+eOJfyKZUbsuM6xKGWY2W/f//j549fwnQZ5ZhZ0uSoW8kRVwVpjrGRf67+uzZriLjXl9TZ8dtX1PFqrYWyYG+qlhkbGmmNmRb9j4zyJR8wSPSAwjG3iR0cqd3o7xYVpJfr9bd4djG+a9YaqetjbkKy3zLZ7fYRPQpEnJZaNdpvz4w3DuPu3L3SZGAOXJfF74YoCCYISrzjH4ZMP80SEN+C7ZzYk68FP4skdWsR5hAfJ6jWa053WdTlmONnOgScmE0PHSWHWRhld/MBFHo/RSI8oXNLntPF8oz5dBecSfvadIZkmo3Dsgi20++pJkh3nfmVmmzQZJQn7KOeIAKUojUYJH58zVsXn0+kX6GpJmdkqPKZRUVKU6gh0XQV1rHXIMqtPXhWl+ujUd0C38JH209d5/DoEC8jftDblT1zBMsys2yrrCvOY2SY071wAz9w7D+RB3Sszs90B3S2VMwzN0FlH8G4WbzF0fABzi7Y6IK71aNQ1VQp3cEysjzU0RBud+ycwibjOSl7CJjzYSZIddy8T8AyhqJQnxV6xGDadfh0ZOlMpK0oVcFzTi6N07nzH189HkXTjql7QNaSOj7QqSopSHYGu1btjrVPOsY67co4tfKRdVzAEp9NRwq8ukHDC7URN+RNXMGVmm9mpCeCZq2nRtrcioMysIHf/cXg3i2MNjdX21mGb6Xc3x8YaGqKNzv0TmERcZyYfuSo82EmSHXcvE/DMQZKpmxR7xlKu6vTryJxTmTpFKQPKoerFUTp3vuPr56NIHsZXvkLXkDwuca2iFOORP1KU8rjEtZNQwtfP2J3i0enno6JnccMkPGMjxSNFqQhN0KAoBWAUizSS4XuZopa4YRLy+GqDSGaY2R+2X48fAkh/FIF3hsCnT5/emUfqjiKgCCgCioAioAgoArchgO8Ou82O9lYEFAFF4NkQ0PXz2TKq8SgCL4FAhpl1LzFwBX2bQcy5+yOcffd9tDQOAd0zK1jefxzezeJYQ2O1jRvIHe++udHoWASGaKMzLfxcdIYkCCke7CRJ5FkryczB8wlRgu/cHiV23M+OsaQoNRGgCY99et7Gi+ucsSo+n06dHU0Eus5cHeNzwuxoxiICXRHN0KkoNVGlKxZ4hMyQbHr4TsYS7qei1MRq0qhr2tWx1LUm49ch5yI/dsYpMwtmMy+Gj7B8f629DQFlZgW/+4/Du1kca2isttsGb9T7bo6NNTRE2yQm8VHO6NE4KB/0XUdOYLrLrkUt+JCYJDn2Com09bBpERblg9N1Kkrl5JiWvhkHMwtNuyLQZ33CfMfXz0eRnIL8hLzjfp4rqWtIE/++WaxjqYkAnTixT49kM48icPpZG/dTUWpipXOzCZG8lfXcsYRfXSDhvMB7Zvdd/sC6/QZheSqx/EptELkPMPu+mR+TjzcDbDTdqubN9t/QUZlZAS0/Dt8AKNzlbhbHGhqrDUarLXg3x8YaGqKNrpBOZRba6WEJPNhJkh1XSBPwfEKU4Hu8R4kd97NjLClKTQRowmOfHpYf13nu+vko1nV2NBHoOnN1jM8Js6MZiwh0RTRDp6LURHUSR4Yj3/TwnYwl3E88dlwSt/4oknjsuOSjxI77iceOS3ZYh+9lcJ0zJPHYEcnMntnPH79++/mXn37+c+NtBtu67tfrvl4u9F352XMUZVCZaxZ1gVCo31TTl6MRfSmUpHIoFnTghlS29zh/1mdk9nXZDuq8fV86CAEVSe9tMbZMPX05ZIy6TJVg48xJQunQyRo1R22uk5GOeoWNrCuqGHmQZ2aFYuZB6XhrOgrqj07kU3mU45p93wTfSH9BOKkODTk91ysT7PWJlCgKDkOdQfWxaP0+tnTWwBZJbxBmVEZsekNR+uR5RDdeXhtiOx0zbzSKmOp2DFGakxlrKNDGKw7901UgF5WZzSUqreu7e4GvZnBWJXWocBwMiYKErZ4kiVz3kAyZxz49bJoNrvE9KfaGVdvcFbui1EZgzlhq25UBfPaTLXwNOVfSDv/Gt86OBkDcrCgpSnUEus5xHWsdfNbGddYDca1dEble9cIknXjsuGQ9ENc6KSKnv17oso7HjkvW3XOtXX66XvXCJJ147LhkPRDXSmcZ+F7G9aoXHgKlDDP77U9/OE5WCvn3zBKRt6/rtq3rti7Ezgq1ty1Sf6XCdaemnQQCmaDysmw7HxowuUwqRUaajIBlPEkhMQBESAo57JRQT7bJLsmREyNPrMLUbj2XpdZ8jrflsiyMiAl/vXxYxC3DUW3rwrgRs81weQGpMf8SNcS4hQgIcSpwimOGmWVClfWFIZPIRu4QJFGmnLzVwm5vlNR930TYZCebQeom/nN+g15uMCQmxNC4f0vMrITsmHGHT1IfOpJPZSjhyvu2rpYL50qj3wlUC95QoEc0ZNn8QFnAkAdFfH/+ti7L6lAhxVYN5ymsCKxmiz6KbHNYGYR5DcuhTLnsDTHjFwJlJoXr64Lwcbk2U/Da0pbCMRPwNxotqI6qux2LenccjDXkte3rSksMr/14gR3vOvvi52lcEoTPB9vqMEkSv+7BY8clW0Gb9kmx49Y7UILv8XDrjyKpKDUzdTr31JEj+O4Fn+/PJ9nMuAicnnfcz3MlO8anrrRNBOjEiX30SSEClOKpKFXXR13nq/CYxtNRwq9DkHBwtqRXEl+9EckMM/vdlx9/+v7r5+/be2aF5mFm9kKk3kXYSOJ/LlQhbO2yym/br16GOUKuFX6RuMCr0EabiNEhb8XlJtqYa/WbekqCIcQMQcOS1G0jjsB0IRrKiMUK2TnpAuYzJ5a/C2VLxGwycUkkLRN53nNmMcT4vi5OQAJx/y4rEarCpYYIUBfS6LcqO+bI1ntkLL9KZi6X1cDLmUr1WP/IAUkGZydIls8C96UW+s/k1/VKxCJXcyi+vS7PzPJQOsBDI4FQ8LBFdvOpjESCAwOw1EQHgVC+GBmyXYmqt48NpBsPgz3g9EmUHyxsHIhh9kU40pk3S2ORnneEzCxTmZztgFWnhx3tH8iiU2PDpIqw7ATKhdiQTA67OESqODyuEehodNIA5sczVn+szdbWvv2YMfOj32hNvW3rd8z27Pwea8hrM6NLnsq5Ba5VYOfp3H8qswBC6INtdZgkiZzRSWYOnq2gTfuk2HHrHSghty76nllFqYkADXrs08Oq4DrPXT8fxbquIU0EulbvjvE5YXY0YxGBrohm6FSUmqhOYn9w5JsevpOxhPuJx45L4tYfRRKPHZd8lNhxP/HYcckO6/C9Ia5zhiQeOyKZYWZ5z+wvn7/84nbOFvbMmm2DzIUy3yWMpOxaNVtXd96uuW20tdbLBJWXi+EtDVaGkCJGxdCSwm8KyyubcIkCJP7IcCTMWrpdjHTk9uoKtWgdDRWmdsFUJWL5s75QOLwBkhhMYtLoX8NmbhvvYGWiTKjbRGAx+3ljZtajx1RpRHcKEEG9Q4ZCXog9DbcSm93NgTyHxcfbJntrqZfd5kxKkgxKLNwQtHJkthcx66mJBL6bDwvMLOkl08wxGjLP2nL1tsJ851OZCLlDAzAdJ/qdSKkQGQr1HJjZgLK/XGhUsDXOpNmvbm1EOm1l/L2vvJP7QoPLtHASaSC5NJXAiVXREWAx6BSEaWdt0FothoacmhxJKqsPTTQORx788EOCYJdwqK1qNmoUWN5sNNJVOHibYwVlteqxhqy2fVsIavkfLvAqrm8zqKXLt/XdvcBXMzir4l2pluyQqApx4yRJ5LqHZMg89ulh09phz4wdt47Hjkvi1h9FEo8dl8Rjx3Xis/iVJacgr2tIEwFdaZsQ6fkIgagTJXz9xFeGR5HEY8clHyV23E88dlwSt/4oknjsuCQeO37FguucIYnHjkhmmNnPX3789uXj55/9Ow3yzCwYXFWsl9XKKouVtH4jnFXEXbJaoUr83hJSZ4TijY09PV9NNsvMOp6RGUjH5jVo4o5U0ts5aP9xoh8E3xsK9OyG+fYkYsLpu5dRLBs/s6D3hPjtr15nw4mwkwdEqEzPxTeUUDNskd8y6+AKQgaMRIbokYu8bkOeZ/AjB0cyb0Rjb5yX5GlQNNc73Gb/wrHknkb0GkUi7XUM0ZmVGWvIaeOBRdx1V0E8JI5sApOI68wCdax0wR6bkppJksgZnWTm4JnEWDqcFHvJXFLfxbfieCZWSoenx15yLKlXlBJAsoeno4SPT3yte2XJbJaPlafn/ehStub01aZjfMK8WzbSY+XpsR9dytboWMrCklROQgkfn4k/pUMddSVkwnpFKUSjVFaUSsiE9bQywPeGYcdKeRLy+GqDSGaYWbdV1hXmMbMV+B6iCc/xQ4TzcE5mmdm3RXG3VM4wNENnHca7WcQMmf2svFe68LoKjgfTVg/dtaJGXYdKYahjFTs9lHpNjWkb4nbX2Rc/T+OSQKAkggc7SRI5o5NMz9XMS6OkfEETARrK2Ed3FiNA9aCEI4/P4leWxNf5DuSRpPOajFt/FElFqZkpOhfDIwSXbNoVgUnXITOs47HPkJwR0bk6FaUm/jo3mxDJXc+5Ywm/YkHCmXcfNxYlZWbBbObF8DNfvr/W3oaAMrOC3/3H4d0sjjU0VtttgzfqfTfHxhoaom0Sk/goZ/RoHJQP+q4j4efML40SfM9cTkvUgk+H0yXHXkeSth7OMUKtfHC6znNR6rA+Yb7jK8OjSJYHWtTSt9LqGtJEgKYx9tE1BAFKUcJQ0lHXRkDnpo6l6OyXHpx+NsSvLlLXC8eTrirbc01GGjbjMszsD9uvxw+lR38UgXeGwKdPn96ZR+qOIqAIKAKKgCKgCCgCtyGA3DTKHvnb7GhvRUARUASeDQFdP58toxqPIvASCGSYWfcSA1fQtxkUyHe6KC41af0dENA9swLy/cfh3SyONTRW28ARfjfHxhoaoo3OtKfu+QLziAc7SbLjqewEPJ8QJfjO7VFix/3sGEuKUhMBmvDYB75ipFUR1nnu+vko1nV2NBHoOnN1jE94JDc9FIEuP8/VqSg18e9b6+CxhCPf9FBH3QPNODyb+AjBJXHrjyKJx45L4rHjVxe4zhmSeOyIpDKzYI7yYvhqle+vtbchoMys4Hf/cXg3i2MNjdV22+CNet/NsbGGhmhTZjYaCoWDvrsXZWab9280drFPD5tWyF5ajU+cSZJ47LhkGmTheFJEBWtpdZd1PHZcMnWocHz6fMfviB5FsoB0Wt2HvK4hTQRoymEfXWkRoBQlDCUddW0EdG7qWEpPgNHx6WdD/Ooi8rt80HUFWFYTtQxH6QZmdt/lb5Tb78jRFznI59ggMhGYfd/ox/6ReBTtN3ZD1d9fTplZwTw/Dmfm424Wxxoaq20gwHdzbKyhIdrorDaBScR1gnnEg50k2b7OlqvMOXg+IUrIRbm+QVVRaiJAEx779LAquE58rXtlSXwF60B+Qt5xP8+VVJSa+A+/YyfMe9aQpocicLrOGWMJ1/koKOF+4rHjkrj1R5HEY8clHyV23E88dlyywzp8b4jrnCGJx45IZpjZz1++fv7y8bsvvzTeZiB/mXxfL5faH0O/Xq97jqIMKnPNglwgFEJpqunLsMNsJBQJyqFY0KHWJehdL+bPZ4zMvi6bdI6MJvpybb6OSo7+9jTstixEyu70XTRhujoNJGgcW03CgjZfpJI35dzNVLk2yrA98L3ziny77XHLd46Z3TeLmWevhcg2TDYfOIet+XwqbWvyvVsjhuvuIcmzhpzCxBB4mNXp+jrlb/DWKUkKdYuJsHOAVwObn0SocOgNifc2caHOQtdMtdeWacxVjTCa05vWdTuWKkCPxxoKtPEiQP90FchtZWaR5PXd48FXMzhTgzg57y+f4taR6x6SobGLffROGAFKURqNEj4+8Vn8ypK6hjQRCE7oDdmu9RMfyQ2rtrnLT9up8T1JJx47LtmIxDZPisiqb3x3WcdjnyHZiMQ2d0VkOzW+J+lUlBq4y30HcsrWa8VTUcKvWJoZF4GHmHEZZva33//42++/fvvTHwAzu6/rtq3rti5E9glXuy3rTvVXKlx3atpJIJAJKi/LtvOhQZXLpFJkpMkIWMaTFBIDYBnK1SuhnmyTXZIjJ0aeWIW+C5jOrFg+x9tyWRZGxIRvjXqUuIYdoxJjxR5zvXNy3fad4SQ+U/AjftURsqa0rQtn4SrmyFPWyiRJ0PEqjl2Ez/W9mDsX/ZQ4YXzFk/XygaS39UK+m6+waQ/Al/pAETkfjQ1ma10gWUi7Ko/M7LYuhCchQF/eGatXMPO8ua3Pp9K2Rt/7tq4uB9TiMxLJ5Q8yhg4Kw+cZCJed0emMH5Qn3jr9ruC6Vgo1i0m30IGwnIgVDr0hZvyM81