Как построить диаграмму "водопад" (waterfall)
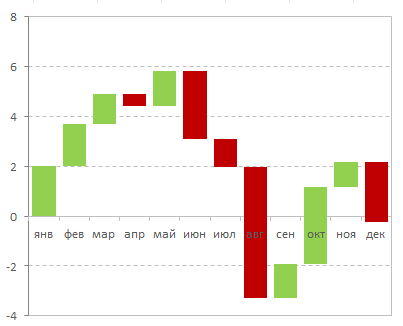
Все чаще и чаще встречаю в отчетности разных компаний и слышу просьбы от слушателей на тренингах объяснить как строится каскадная диаграмма отклонений - она же "водопад", она же "waterfall", она же "мост", она же "bridge" и т.д. Выглядит она примерно так:
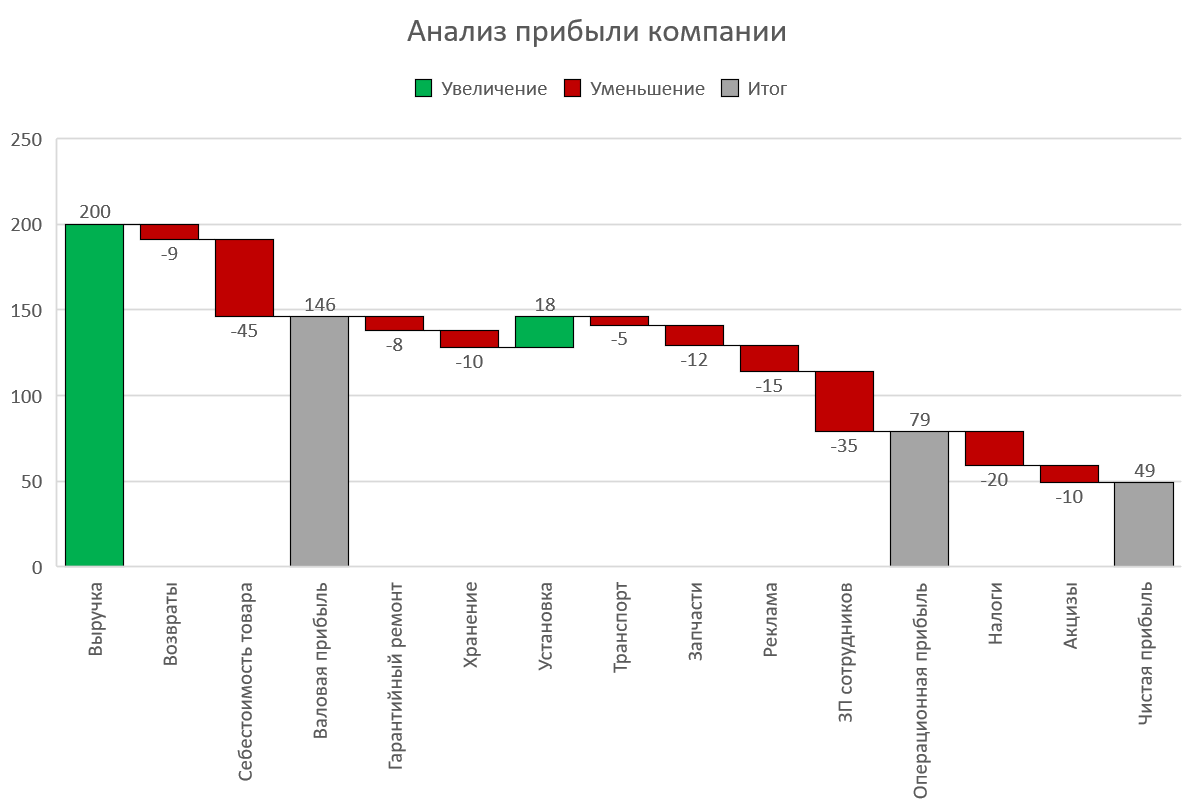
Издали действительно похожа на каскад водопадов на горной реке или навесной мост - кто что видит :)
Особенность такой диаграммы том, что:
- Мы наглядно видим начальное и конечное значение параметра (первый и последний столбцы).
- Положительные изменения (рост) отображаются одним цветом (обычно зеленым), а отрицательные (спад) - другим (обычно красным).
- Иногда в диаграмме могут присутствовать ещё и столбцы промежуточных итогов (серые, приземленные на ось Х столбцы).
В повседневной жизни такие диаграммы используются обычно в следующих случаях:
- Наглядное отображение динамики какого-либо процесса во времени: потока наличности (cash-flow), инвестиций (вкладываем деньги в проект и получаем от него прибыль).
- Визуализация выполнения плана (крайний левый столбик в диаграмме - факт, крайний правый - план, вся диаграмма отображает наш процесс движения к желаемому результату)
- Когда нужно наглядно показать факторы, влияющие на наш параметр (факторный анализ прибыли - из чего она складывается).
Есть несколько способов построения такой диаграммы - всё зависит от вашей версии Microsoft Excel.
Способ 1. Самый простой: встроенный тип в Excel 2016 и новее
Если у вас Excel 2016, 2019 или новее (или Office 365), то построение такой диаграммы не составит труда - в этих версиях Excel такой тип уже встроен по умолчанию. Нужно будет лишь выделить таблицу с данными и выбрать на вкладке Вставка (Insert) команду Каскадная (Waterfall):
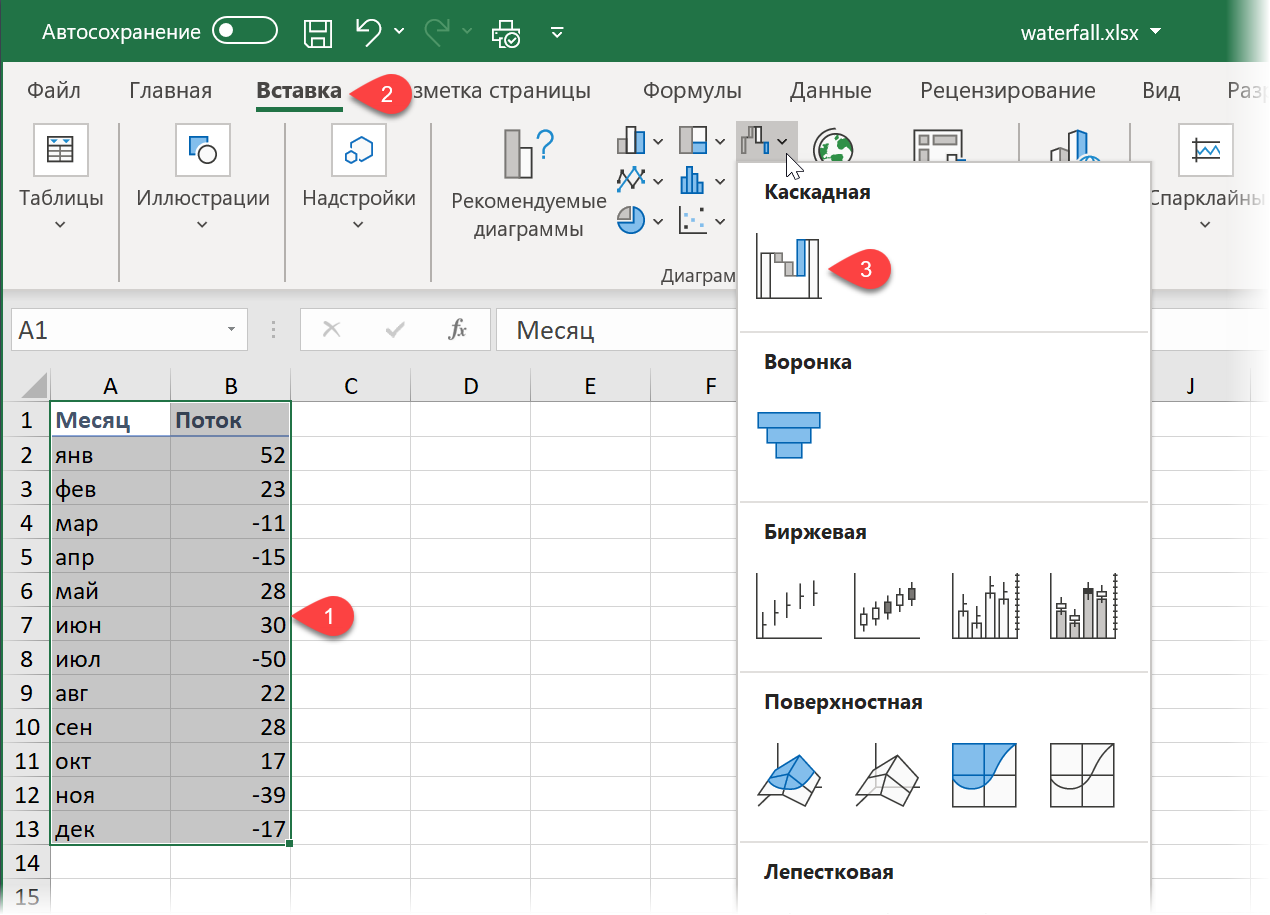
В результате мы получим практически готовую уже диаграмму:
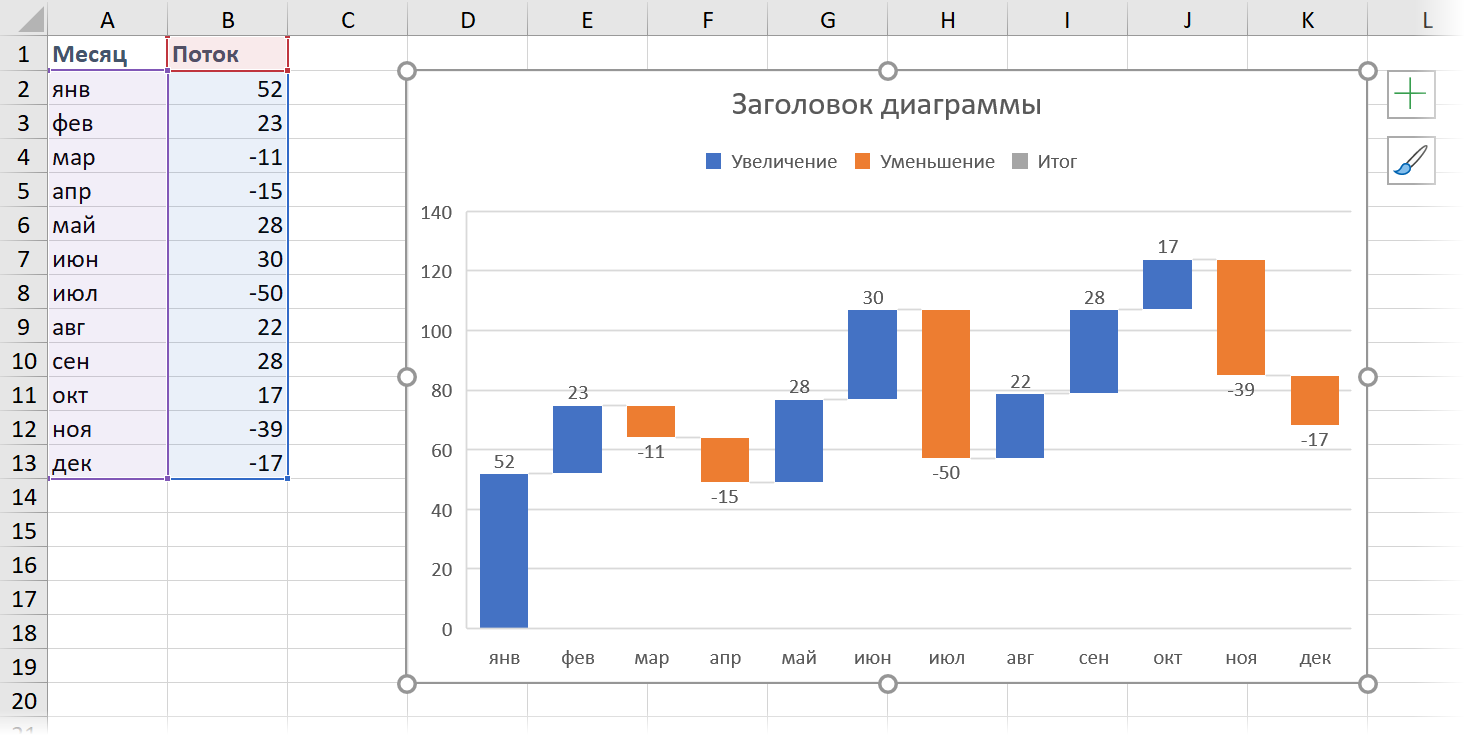
Сразу же можно настроить желаемые цвета заливки для положительных и отрицательных столбцов. Удобнее всего это сделать, выделив соответствующие ряды Увеличение и Уменьшение прямо в легенде и, щёлкнув по ним правой кнопкой мыши, выбрать команду Заливка (Fill):
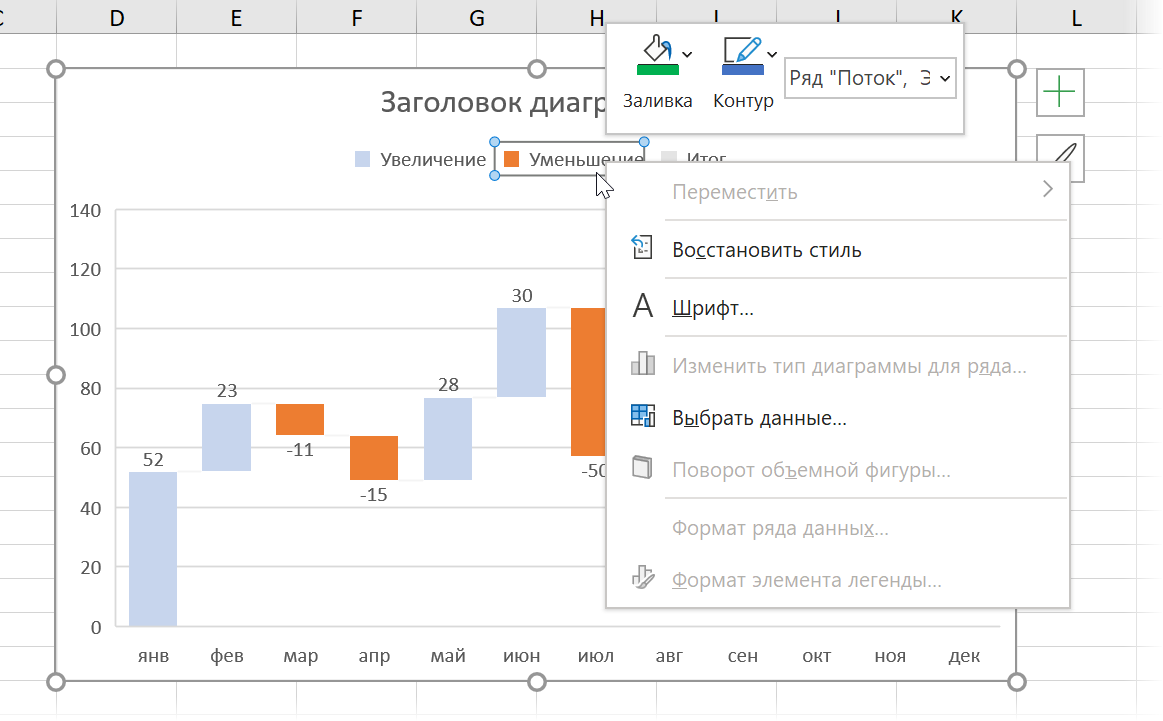
Если нужно добавить в диаграмму столбцы с промежуточными итогами или финальный столбец-итог, то удобнее всего это сделать с помощью функций ПРОМЕЖУТОЧНЫЕ.ИТОГИ (SUBTOTALS) или АГРЕГАТ (AGGREGATE). Они посчитает накопленную с начала таблицы сумму, исключив при этом из нее выше расположенные аналогичные итоги:
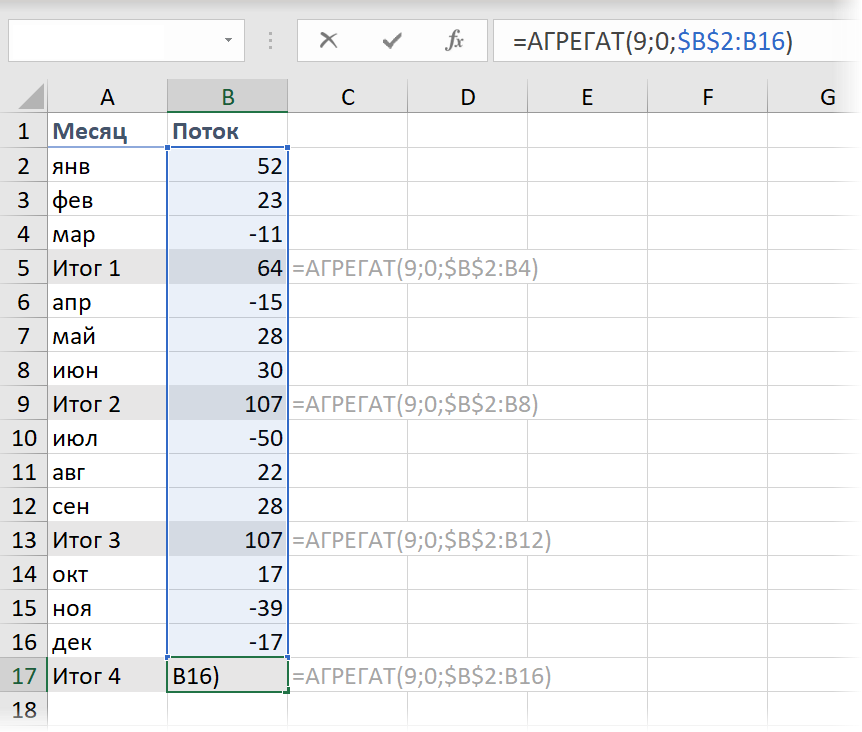
В данном случае, первый аргумент (9) - это код математической операции суммирования, а второй (0) заставляет функцию не учитывать в результатах уже вычисленные итоги за предыдущие кварталы.
После добавления строк с итогами останется выделить на диаграмме появившиеся итоговые колонки (сделать два последовательных одиночных щелчка по столбцу) и, щёлкнув правой кнопкой мыши, выбрать команду Установить в качестве итога (Set as total):
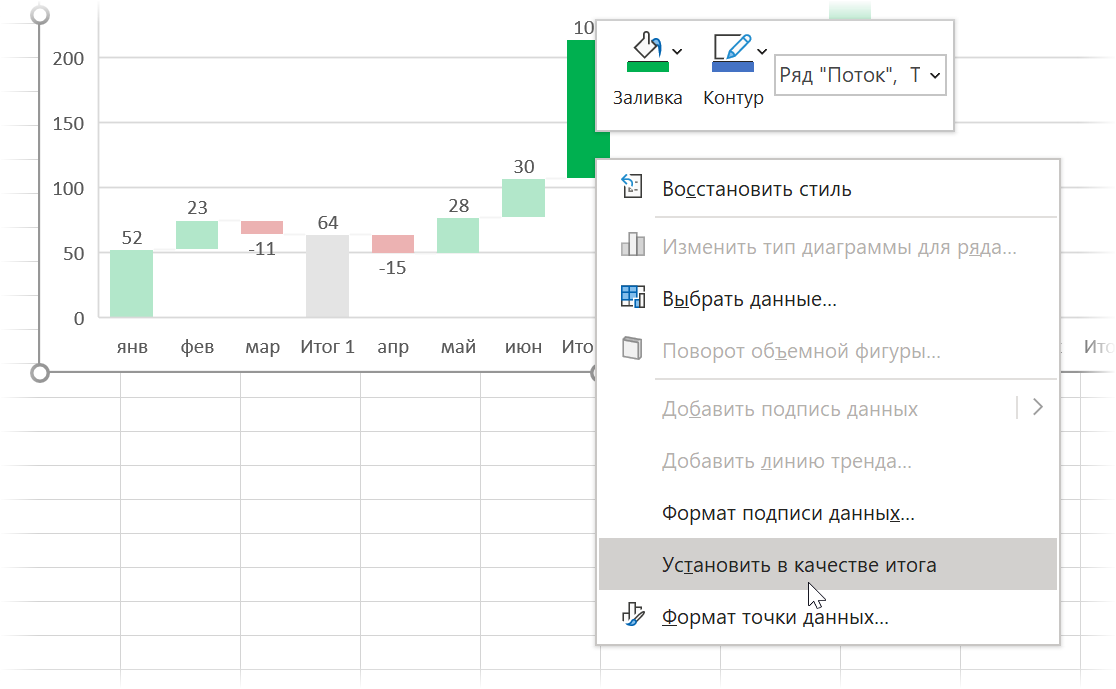
Выбранный столбец "приземлится" на ось Х и автоматически поменяет цвет на серый.
Вот, собственно, и всё - диаграмма-водопад готова:
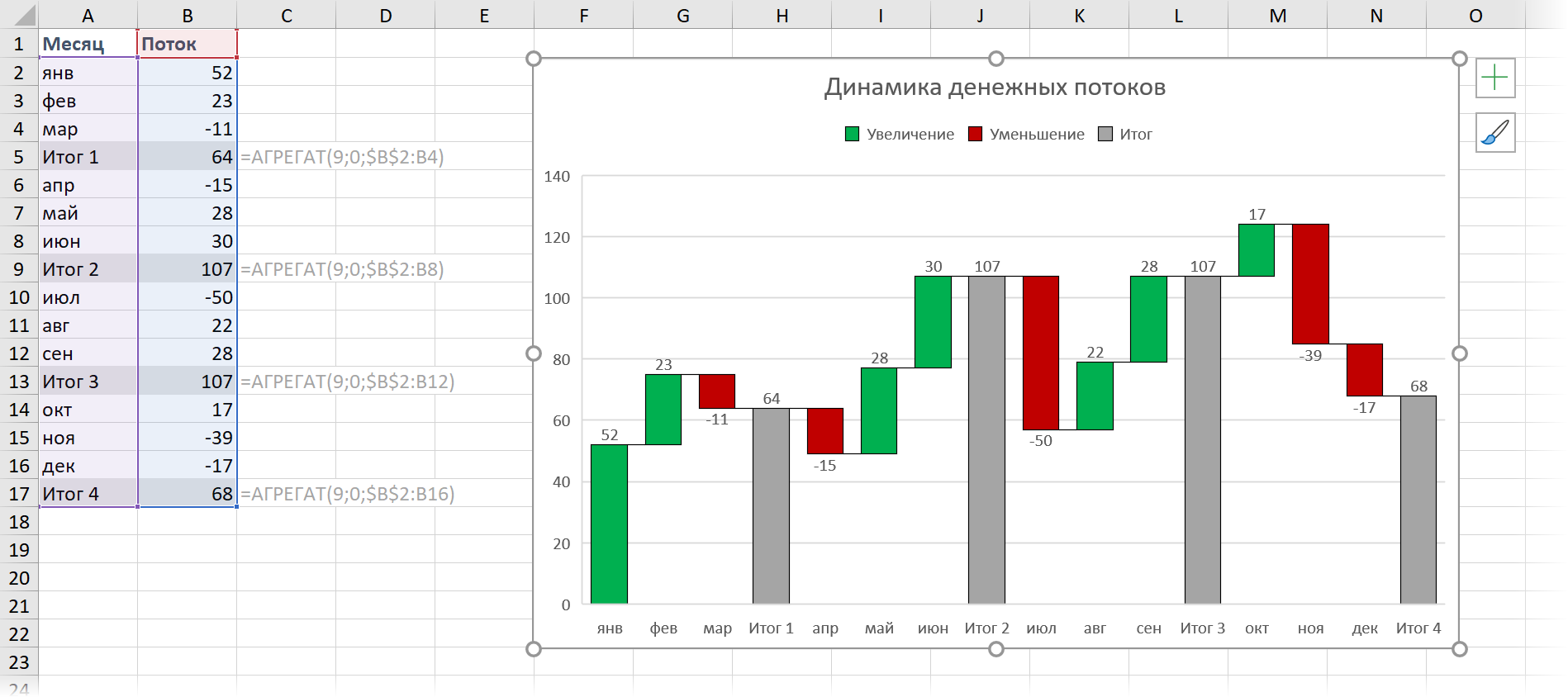
Способ 2. Универсальный: невидимые столбцы
Если у вас Excel 2013 или более древние версии (2010, 2007 и т.д.), то описанный выше способ вам не подойдёт. Придется идти обходным путем и выпиливать недостающую каскадную диаграмму из обычной гистограммы с накоплением (суммированием столбиков друг на друга).
Хитрость тут заключается в использовании прозрачных столбцов-подпорок, приподнимающих наши красные и зеленые ряды данных на нужную высоту:
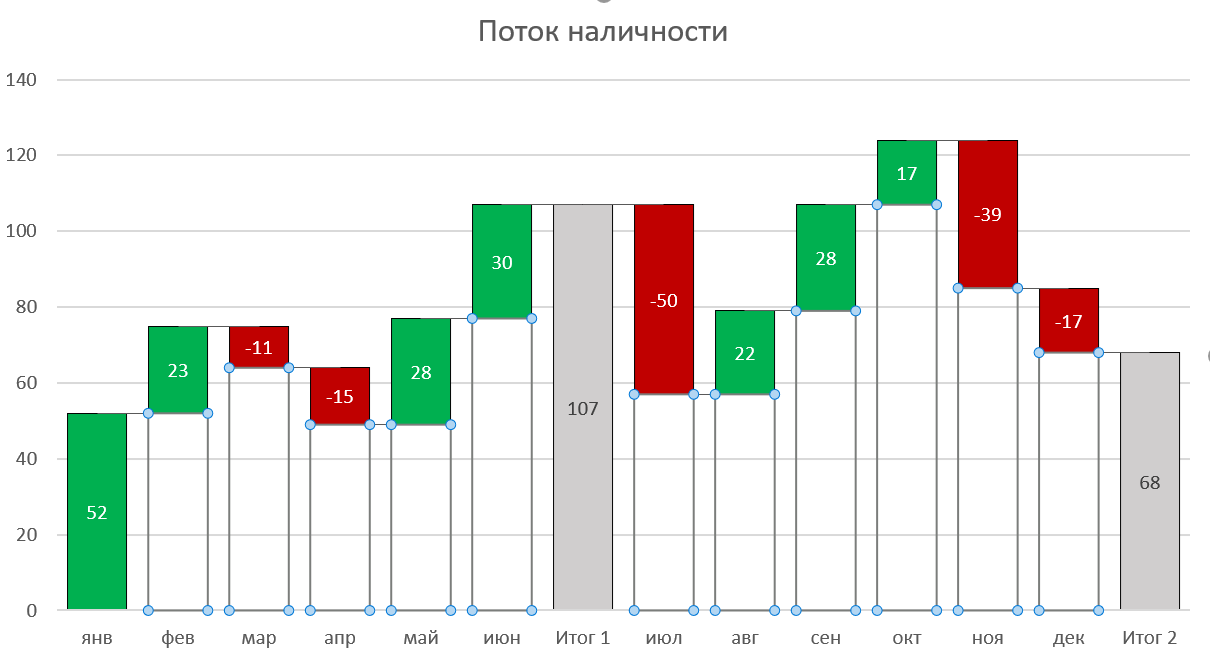
Для построения такой диаграммы нам потребуется добавить к исходным данным еще несколько вспомогательных колонок с формулами:
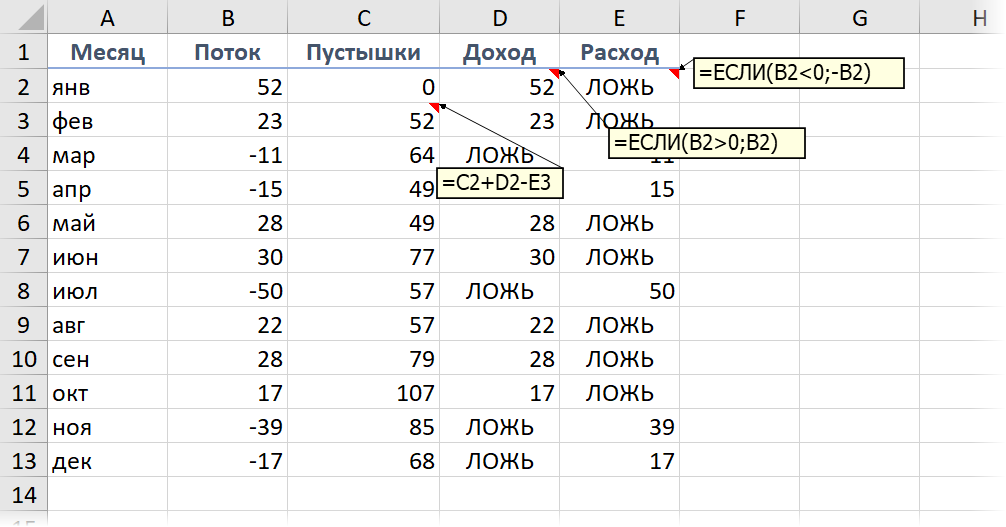
- Во-первых, нужно разделить наш исходный столбец, выделив положительные и отрицательные значения в разные колонки с помощью функции ЕСЛИ (IF).
- Во-вторых, нужно будет добавить перед сделанными столбцами колонку Пустышки, где первое значение будет 0, а начиная со второй ячейки формулой будет вычисляться высота тех самых прозрачных подпирающих столбцов.
После этого останется выделить всю таблицу кроме исходного столбца Поток и создать обычную гистограмму с накоплением через Вставка - Гистограмма (Insert - Column Chart):
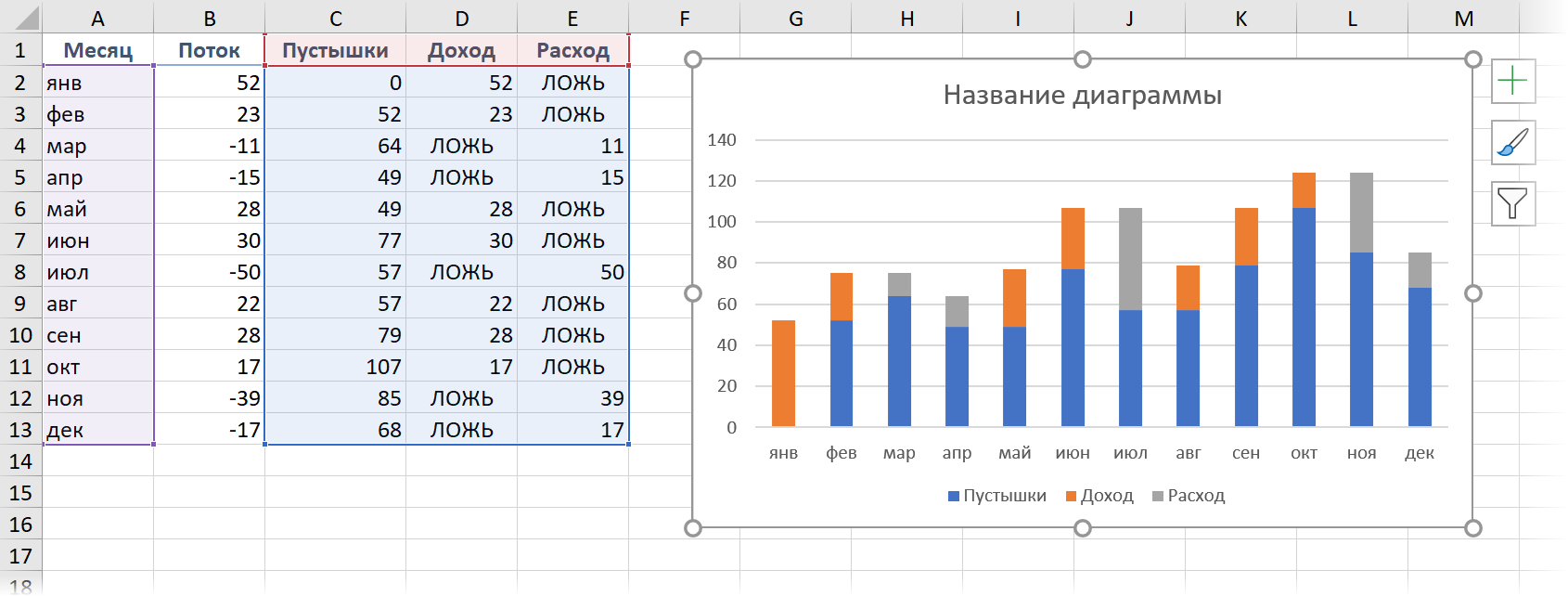
Если теперь выделить синие столбцы и сделать их невидимыми (по ним правой кнопкой мыши - Формат ряда - Заливка - Нет заливки), то мы как раз и получим то, что требуется.
В плюсах подобного способа - простота. В минусах - необходимость считать вспомогательные колонки.
Способ 3. Если уходим в минус - всё сложнее
К сожалению, предыдущий способ адекватно работает только для положительных значений. Если хотя бы на каком-то участке наш водопад уходит в отрицательную область, то сложность задачи возрастает в разы. В этом случае необходимо будет формулами просчитать каждый ряд (пустышки, зеленые и красные) отдельно для отрицательной и положительной частей:
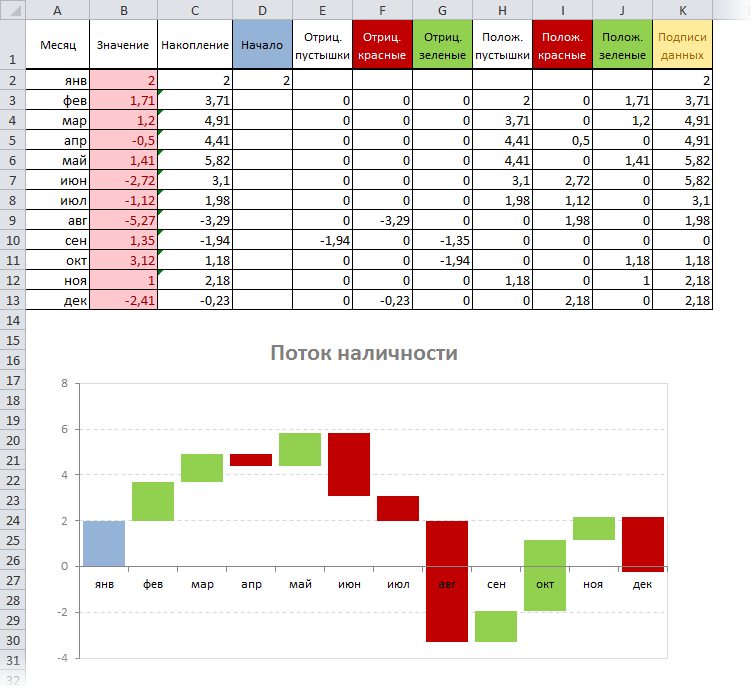
Чтобы не сильно мучиться и не изобретать велосипед, готовый шаблон для такого случая можно скачать в заголовке этой статьи.
Способ 4. Экзотический: полосы повышения-понижения
Этот способ основан на использовании специального малоизвестного элемента плоских диаграмм (гистограмм и графиков) - Полос повышения-понижения (Up-Down Bars). Эти полосы попарно соединяют точки двух графиков, чтобы наглядно показать какая из двух точек выше-ниже, что активно используется при визуализации план-факта:
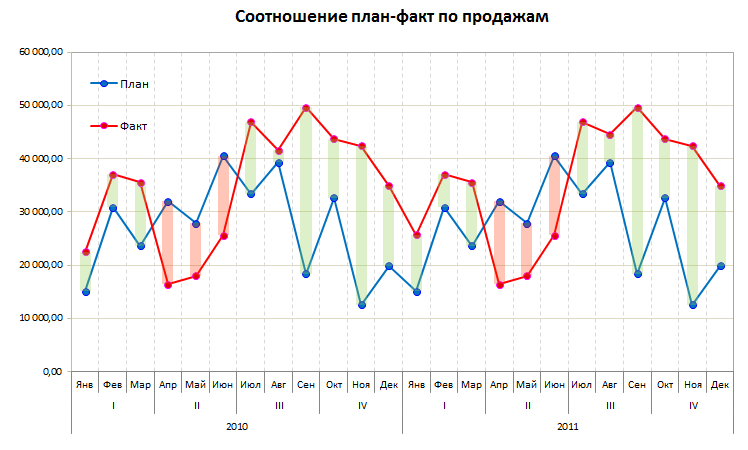
Легко сообразить, что если убрать линии графиков и оставить на диаграмме только полосы повышения-понижения, то мы получим все тот же "водопад".
Для такого построения нам потребуется добавить к нашей таблице еще два дополнительных столбца с простыми формулами, которые расчитают положение двух требуемых невидимых графиков:
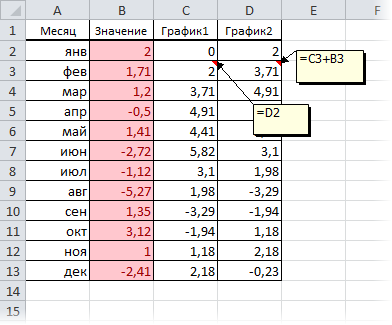
Для создания "водопада" нужно выделить столбец с месяцами (для подписей по оси Х) и два дополнительных столбца График 1 и График 2 и построить для начала обычный график через Вставка - График (Insert - Line Сhart):
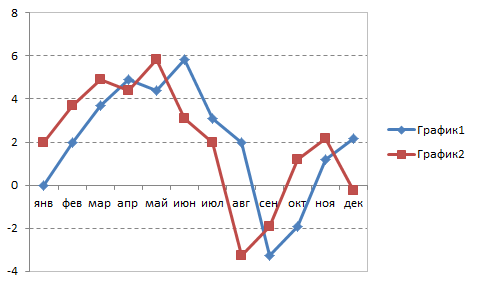
Теперь добавим к нашей диаграмме полосы повышения-понижения:
- В Excel 2013 и новее для этого необходимо выбрать на вкладке Конструктор команду Добавить элемент диаграммы - Полосы повышения-понижения (Design - Add Chart Element - Up-Down Bars)
- В Excel 2007-2010 - перейти на вкладку Макет - Полосы повышения-понижения (Layout - Up-Down Bars)
Диаграмма после этого начнёт выглядеть примерно так:
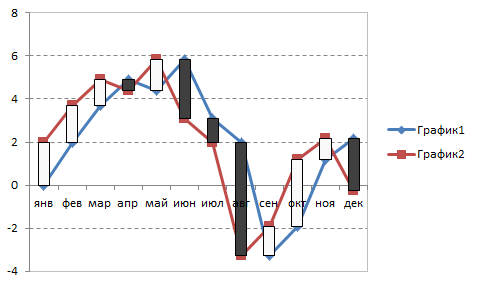
Осталось выделить графики и сделать их прозрачными, щелкнув по ним по очереди правой кнопкой мыши и выбрав команду Формат ряда данных (Format series). Аналогичным образом можно изменить и стандартные, весьма убого выглядящие, чёрно-белые цвета полос на зелёные и красные, чтобы получить в итоге более приятную картинку:
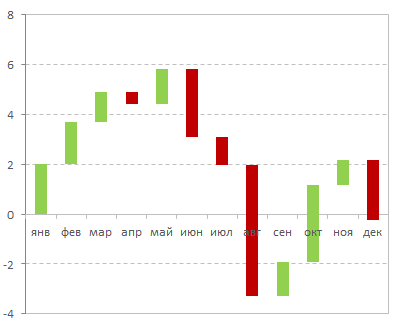
В последних версиях Microsoft Excel ширину полос можно изменить, щёлкнув по одному из прозрачных графиков (не по полосам!) правой кнопкой мыши и выбрав команду Формат ряда данных - Боковой зазор (Format series - Gap width).
В старых версиях Excel для такого исправления приходилось использовать команду на Visual Basic:
- Выделите построенную диаграмму
- Нажмите сочетание клавиш Alt+F11, чтобы попасть в редактор Visual Basic
- Нажмите сочтетание клавиш Ctrl+G, чтобы открыть панель прямого ввода команд и отладки Immediate (обычно она расположена внизу).
- Скопируйте и вставьте туда вот такую команду: ActiveChart.ChartGroups(1).GapWidth = 30 и нажмите Enter:
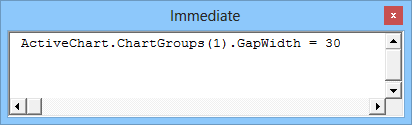
При желании можно, конечно, поиграться со значением параметра GapWidth, чтобы добиться нужной величины зазора:

Если отклонения незначительны, то они показываются тонкой полоской, вместо ожидаемого длинного столбца...
Формат ряда данных - Параметры ряда - Боковой зазор
Уменьшаем до нуля и пожалуйста, достаточно приличной ширины становятся полосы понижения/повышения.
По крайней мере так в Excel 2010
Суть: построение гистограммы по месяцам, НО, отталкивающейся от нулевой оси?
Например, Январь +100 - зеленая колонка поднимается вверх от нулевой оси, а если по полученным данным в феврале -20 - красный столбец опускается ниже нулевой оси.
Заранее благодарю за вашу помощь и подсказку!!
Пришлось только ссылку на файлообменник делать.
Есть данные по месяцам. Допустим, январь = 100%. Каждый следующий месяц сравниваем с предыдущим и добавляем нулевой столбец. На базе 1, 3 и 4 колонки строим график как в способе 2. Вуаля)))